The statistical mechanical basis of the triple isotope fractionation relationship
Affiliations | Corresponding Author | Cite as | Funding informationKeywords: three isotope relationship, mass-dependent fractionation, isotope fractionation
- Share this article





Article views:11,065Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract
Figures and Tables
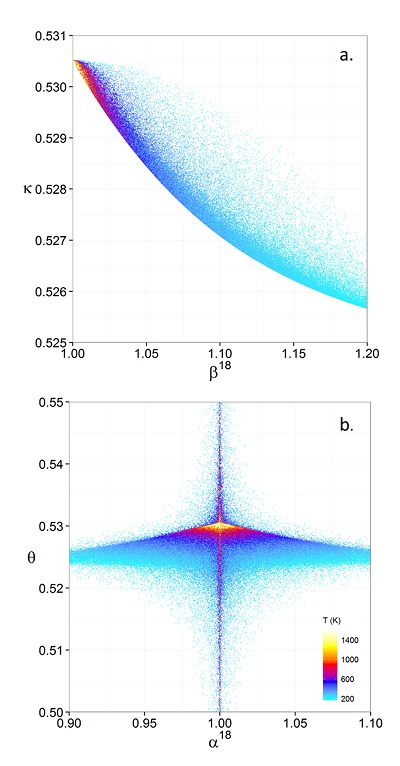 Figure 1 (a) β18 vs. κ and (b) Equilibrium α18 vs. θ plots for randomly selected hypothetical diatomic molecules under the harmonic approximation in the 16O-17O-18O system. Temperature is plotted as colour on the same scale for both plots. The model uses 1,000,000 evenly distributed randomly generated values for the secondary mass (0-300 AMU), the bond force constant (0-kUL), and temperature (200-1600 oK). The bond force constant for carbon monoxide (CO) is used as an arbitrary upper limit (UL) for the bond force constant for diatomic oxygen species. | 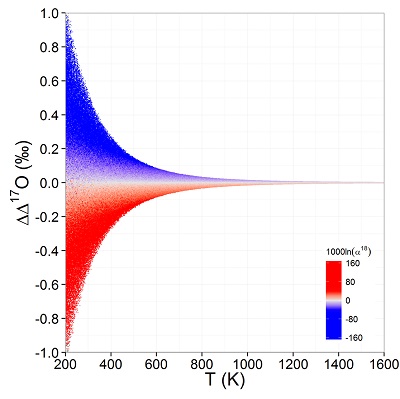 Figure 2 Temperature vs. Δ(Δ17O) plot for equilibrium between randomly selected diatomic molecules under the harmonic approximation in the 16O-17O-18O system. A C value of 0.5305 (HTL) is used for the Δ(Δ17O) definition. 1000 ln α18 is plotted as colour. The range of Δ(Δ17O) values in this plot is expected to be an overestimate for natural samples. The points in this model each correspond to a point in Figure 1a. |  Figure 3 Three isotope fractionation parameters for haematite synthesis conducted by Bao and Koch (1999). Values are calculated from newly measured δ18Ohaematite and δ18Owater values, and an assumed Δ17O (C = 0.528) of 0.02 ‰ for the water based on reported Baltimore tap water from Li et al. (2015). Δ(Δ17O) are reported using C = 0.5305. The method for calculating uncertainties can be found in the Supplementary Information. Best fit curves for the ln (α) values are second order polynomials of 1/T. The best fit curves for Δ(Δ17O) and θ are calculated from the fits to ln (α). |
| Figure 1 | Figure 2 | Figure 3 |
Supplementary Figures and Tables
 Table S-1 Results from both previous δ18O (converted to logarithmic definition) measurements from Bao and Koch (1999) and new δ’18O and Δ17O analysis from this study. δ'17O values for the water are calculated using the δ’18O values for the water measured by Bao and Koch (1999) and published Δ17O values for Baltimore tap water (Li et al., 2015). Values of α are for haematite precipitation with oxygen sourced from water (αhaematite-water). The method for determining uncertainties is described in the text of the Supplementary Information. All uncertainties are 1 σ. |
| Table S-1 |
top
Introduction
Despite roots in physical chemistry, the study of triple isotope relationships has found its most widespread and varied footing in the realm of geochemistry and cosmochemistry. Multiple stable isotope ratios have, among other uses, found utility as tools to elucidate photochemical (Farquhar et al., 2000
Farquhar, J., Bao, H.M., Thiemens, M. (2000) Atmospheric influence of Earth's earliest sulfur cycle. Science 289, 756-758.
; Bao et al., 2008Bao, H.M., Lyons, J.R., Zhou, C.M. (2008) Triple oxygen isotope evidence for elevated CO2 levels after a Neoproterozoic glaciation. Nature 453, 504-506.
) or magnetic isotope effects (Blum et al., 2014Blum, J.D., Sherman, L.S., Johnson, M.W. (2014) Mercury isotopes in Earth and Environmental Sciences. In: Jeanloz, R. (Ed.) Annual Review of Earth and Planetary Sciences. Vol 42. Annual Reviews, Palo Alto, 249-269.
) and as an identifying marker for extraterrestrial materials (Clayton et al., 1973Clayton, R.N., Grossman, L., Mayeda, T.K. (1973) Component of primitive nuclear composition in carbonaceous meteorites. Science 182, 485-488.
). Because of advances in analytical resolution, now more than ever, it is critical to understand the natural range of multiple isotope relationships to further these pursuits. The three isotope relationship was recently re-investigated for complex processes by Bao et al. (2015)Bao, H., Cao, X., Hayles, J.A. (2015) The confines of triple oxygen isotope exponents in elemental and complex mass-dependent processes. Geochimica et Cosmochimica Acta 170, 39-50.
using a broadly approximate treatment for elemental processes (i.e. equilibrium and kinetic isotope effects). The intrinsic relationships among temperature (T), isotope fractionation factor (α), and three-isotope exponent (θ) in mass-dependent elemental processes at equilibrium have not been explored theoretically.The first accurate model for predicting the separation of isotopes for equilibrium processes was published independently by Urey (1947)
Urey, H.C. (1947) The thermodynamic properties of isotopic substances. Journal of the Chemical Society, 562-581.
and Bigeleisen and Goeppert-Mayer (1947; the B-GM-U model)Bigeleisen, J., Mayer, M.G. (1947) Calculation of equilibrium constants for isotopic exchange reactions. Journal of Chemical Physics 15, 261-267.
. Their development of the concept of reduced partition function ratio (RPFR or (s/s’)f) allowed for the calculation of α between two species using only the harmonic vibrational frequencies for each degree of freedom and temperature.Eq. 1
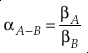
where A and B indicate different chemical species. Using oxygen as an example, 18αA-B = ([18O]/[16O])A/([18O]/[16O])B and 18βA = ([18O]/[16O])A/([18O]/[16O])Atomic-O. Under the harmonic approximation, β can be calculated by
Eq. 2
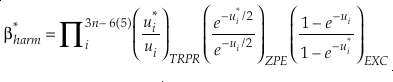
Eq. 3
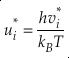
Here, h is the Planck constant, kB is Boltzmann’s constant and T is temperature in kelvin, υ is the harmonic vibrational frequency for a specific vibrational degree of freedom and the product is taken over all vibrational degrees of freedom, the number of which is given by 3n-6 for non-linear molecules and 3n-5 for linear molecules where n is the number of atoms in that molecule. The heavy isotope substituted state is indicated by “*” and the lack of a superscript indicates the reference isotope (commonly the most abundant isotope). The harmonic contribution can be separated into the product of three terms: (a) the Teller-Redlich product rule (TRPR) term; (b) the zero-point energy (ZPE) contribution; and (c) non-zero point energy contributions (EXC) (Wolfsberg, 1972
Wolfsberg, M. (1972) Theoretical evaluation of experimentally observed isotope-effects. Accounts of Chemical Research 5, 225.
). Importantly, the β in Equation 2 is modified with a subscript “harm” to indicate that this term only represents the contributions to isotope partitioning from the harmonic portions of molecular vibrations. The B-GM-U model is successful as it gives the dominant contribution to the value of β to a point near or better than analytical precision for most isotope systems. However, for molecules bearing light isotopes, particularly hydrogen, contributions from anharmonicity, non-classical rotations and rotational-vibrational interactions become significant. Modifications of the B-GM-U model in the form of multiplicative terms have been developed to correct these inaccuracies. Here we use the term “contribution” to specifically indicate multiplicative terms. Each contribution (e.g., harmonic vibrational, anharmonic vibrational, rotational, imaginary etc.) is treated as having its own parameter, such as β, which is only a portion of the complete parameter.top
Extension to Three Isotope Effects
Transformation of a two-isotope model to a three-isotope model involves combining two independently calculated models that use the same reference isotope. A key aspect for the B-GM-U model is the mass dependence of isotope fractionation due to the mass dependence of vibrational frequencies. This relationship can be described by an exponent θ where
Eq. 4
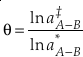
where “‡” and “*” indicate the respective parameters for two different isotope ratios of the same element. Due to the use of the “low-u” (see Eq. 3) approximation of Equation 2, it was commonly believed that the value of the three isotope exponent was somewhat constant and later thought to be constrained to a finite, “canonical”, range for mass-dependent processes which remains as an accepted idea (Swain et al., 1958
Swain, C.G., Stivers, E.C., Reuwer, J.F., Schaad, L.J. (1958) Use of hydrogen isotope effects to identify the attacking nucleophile in the enolization of ketones catalyzed by acetic acid. Journal of the American Chemical Society 80, 5885-5893.
; Matsuhisa et al., 1978Matsuhisa, Y., Goldsmith, J.R., Clayton, R.N. (1978) Mechanisms of hydrothermal crystallization of quartz at 250 °C and 15 kbar. Geochimica et Cosmochimica Acta 42, 173-180.
; Young et al., 2002Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095-1104.
, 2016Young, E.D., Kohl, I.E., Warren, P.H., Rubie, D.C., Jacobson, S.A., Morbidelli, A. (2016) Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Science 351, 493-496.
; Kaiser et al., 2004Kaiser, J., Rockmann, T., Brenninkmeijer, C.A.M. (2004) Contribution of mass-dependent fractionation to the oxygen isotope anomaly of atmospheric nitrous oxide. Journal of Geophysical Research-Atmospheres 109, 11.
). Here, “canonical” refers to a θ value being within certain range represented by most of the observed cases and theoretical justifications (e.g., 0.50-0.5305 for the 16O-17O-18O system; Eiler et al., 2013Eiler, J., Cartigny, P., Hofmann, A.E., Piasecki, A. (2013) Non-canonical mass laws in equilibrium isotopic fractionations: Evidence from the vapor pressure isotope effect of SF6. Geochimica et Cosmochimica Acta 107, 205-219.
).Using a theoretical framework which represented strictly mass dependent scenarios, Skaron and Wolfsberg (1980)
Skaron, S., Wolfsberg, M. (1980) Anomalies in the fractionation by chemical-equilibrium of O-18-O-16 relative to O-17-O-16. Journal of Chemical Physics 72, 6810-6811.
showed theoretically for oxygen isotope partitioning that θ can vary from positive to negative infinity for crossover scenarios, situations where the fractionation factor α for transitions from greater than 1 (heavier isotopes partitioned to A) to less than 1 (heavier isotopes partitioned to B) or vice-versa with changing temperature. Studies investigating these scenarios for sulphur (Deines, 2003Deines, P. (2003) A note on intra-elemental isotope effects and the interpretation of non-mass-dependent isotope variations. Chemical Geology 199, 179-182.
; Otake et al., 2008Otake, T., Lasaga, A.C., Ohmoto, H. (2008) Ab Initio Calculations For Equilibrium Fractionations In Multiple Sulfur Isotope Systems. Chemical Geology 249, 357-376.
) and hydrogen (Kotaka et al., 1992Kotaka, M., Okamoto, M., Bigeleisen, J. (1992) Anomalous mass effects in isotopic exchange equilibria. Journal of the American Chemical Society 114, 6436-6445.
) have come to the same conclusion.Analogously to the concept of β, Cao and Liu (2011)
Cao, X.B., Liu, Y. (2011) Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes. Geochimica et Cosmochimica Acta 75, 7435-7445.
first introduced the concept of κ defined as the one species analogue of θ, orEq. 5
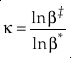
where β is the one species fractionation factor for the two-isotope system. The complete value of κ including all contributions can be calculated by
Eq. 6
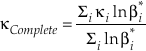
where the sums are taken over all contributions whether they are from corrections (rotational, anharmonic etc.) to the B-GM-U model, from the imaginary frequency contribution for a transition state or from independent vibrational degrees of freedom. As long as all values of ln β have the same sign, such as for harmonic vibrational degrees of freedom, the value of κ for a complex molecule is equal to the ln β weighted mean of the κ values from each contribution. The relationship between κ and θ is given by (Cao and Liu, 2011
Cao, X.B., Liu, Y. (2011) Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes. Geochimica et Cosmochimica Acta 75, 7435-7445.
)Eq. 7
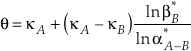
From Equation 7, a large difference in the values of κ between phases A and B allows for a larger variability in the value of θ particularly where α is near unity. The only scenario which would not allow the above conditions to occur for any system would be if the values of κ and β were related by an explicit function of one-another which could be universally applied to all species. This hypothetical case is invalid (see Fig. 1a) because the relationship between vibrational frequencies of differently substituted molecules is a function of not only the mass of the substituted atom, but also the molecular configuration, bond force constants, and masses of secondary, non-substituted atoms. Additional evidence against a universal κ - β* relationship can be found in studies implicating crossovers for θ values approaching infinity (Kotaka et al., 1992
Kotaka, M., Okamoto, M., Bigeleisen, J. (1992) Anomalous mass effects in isotopic exchange equilibria. Journal of the American Chemical Society 114, 6436-6445.
; Deines, 2003Deines, P. (2003) A note on intra-elemental isotope effects and the interpretation of non-mass-dependent isotope variations. Chemical Geology 199, 179-182.
; Otake et al., 2008Otake, T., Lasaga, A.C., Ohmoto, H. (2008) Ab initio calculations for equilibrium fractionations in multiple sulfur isotope systems. Chemical Geology 249, 357-376.
).top
Theoretical Values of κ
The complete equation for the harmonic contribution to κ for a single degree of freedom is given by
Eq. 8
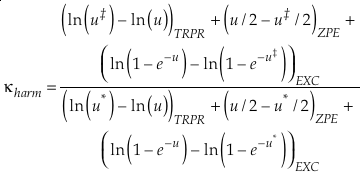
which can be separated into terms that correspond to the contributions from TRPR, ZPE and EXC with each having their own mass dependence. At high temperatures, the contribution from energised states (EXC) dominates the harmonic κ. In this instance the values of u become very small and
Eq. 9
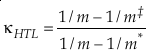
where m, m‡ and m* are the masses of the light, middle and heavy isotopes respectively. Equation 9 serves as an upper bound of its value for diatomic molecules at all temperatures (e.g., κHTL ≈ 0.5305 for the 16O-17O-18O system). At low temperatures, the contribution from ZPE dominates the harmonic κ. For a diatomic molecule under these conditions
Eq. 10

where μ is the reduced mass (μ = m M / [m + M] for a diatomic molecule where M is the secondary, non-substituted mass). In this case, the value of κ decreases with increasing mass of the non-substituted atom (Cao and Liu, 2011
Cao, X.B., Liu, Y. (2011) Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes. Geochimica et Cosmochimica Acta 75, 7435-7445.
). The limit of Equation 10 as the non-substituted mass approaches infinity is thenEq. 11
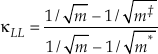
which serves as an unattainable lower boundary of κ for diatomic molecules (e.g., κLL ≈ 0.5232 for the 16O-17O-18O system). Equation 10 is the same as the approximation to the mass fractionation law used by Swain et al. (1958)
Swain, C.G., Stivers, E.C., Reuwer, J.F., Schaad, L.J. (1958) Use of hydrogen isotope effects to identify the attacking nucleophile in the enolization of ketones catalyzed by acetic acid. Journal of the American Chemical Society 80, 5885-5893.
for triple-hydrogen system. Using the arguments of Swain et al. (1958)Swain, C.G., Stivers, E.C., Reuwer, J.F., Schaad, L.J. (1958) Use of hydrogen isotope effects to identify the attacking nucleophile in the enolization of ketones catalyzed by acetic acid. Journal of the American Chemical Society 80, 5885-5893.
, it is expected that polyatomic molecules will behave within or near the diatomic boundaries of κharm presented here. For all calculated results for hypothetical diatomic molecules, the values of κharm are found to not exceed the boundaries given by Equations 9 and 11.Figure 1 displays the relationships between (a) β and κ and (b) θ and α for equilibrium between hypothetical diatomic molecules containing oxygen under the harmonic approximation with temperature plotted as colour. A key finding here is that the diatomic model allows θ to hold any value for small fractionations. Polyatomic molecules incorporate additional degrees of freedom which will weaken the relationship between κ and β. Therefore, this result is a conservative estimate of the distribution of θ. Much like values of α for a two isotope system, the variability of θ becomes greater at lower temperatures. Because anharmonic corrections are small relative to the harmonic contribution and have a similar mass dependency, anharmonic corrections do not have a significant effect on the distribution of θ values. The effects of anharmonic corrections are addressed in more depth in the Supplementary Information. For kinetic isotope effects, the value of κ for the transition states imaginary frequency contribution is also discussed in the Supplementary Information. The results indicate that values of θ for kinetic isotope effects are more variable and on average, but not strictly, lower than those of equilibrium isotope effects.

Figure 1 (a) β18 vs. κ and (b) Equilibrium α18 vs. θ plots for randomly selected hypothetical diatomic molecules under the harmonic approximation in the 16O-17O-18O system. Temperature is plotted as colour on the same scale for both plots. The model uses 1,000,000 evenly distributed randomly generated values for the secondary mass (0-300 AMU), the bond force constant (0-kUL), and temperature (200-1600 oK). The bond force constant for carbon monoxide (CO) is used as an arbitrary upper limit (UL) for the bond force constant for diatomic oxygen species.
top
Change/Difference in Cap-Delta
Although κ is expected to be bounded to a first-order approximation by the high temperature and lower limits as described above, the more common mass-dependent fractionation exponent, θ, is not. What is needed is an additional descriptor for multiple isotope fractionation relationships that is bounded for small isotope effects.
Measured multiple isotope relationships are commonly expressed in the “cap-delta” notation.
Eq. 12
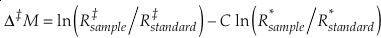
typically either in “per mille” or “per meg”, where C is a somewhat arbitrary constant and R is the molar ratio of one isotope and a reference isotope of the same element. For example, Δ‡M becomes Δ17O for the 16O-17O-18O system and ln (R‡sample/R‡standard) = δ'17 O.
The change, or difference in cap-delta, i.e. Δ‡M through a fractionation process is then
Eq. 13
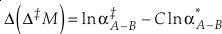
or reduced to more fundamental parameters
Eq. 14
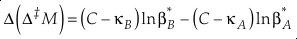
Current analytical precision for Δ‡M can be as low as 0.002 ‰ depending on the element, technique, and species analysed allowing for the resolution of Δ‡M well within the natural range for many commonly explored light elements (e.g., for oxygen in Fig. 2). Using the 16O-17O-18O system as an example, if the arbitrary upper limit of β is given as 1.100 and using the boundaries of κ proposed above for equilibrium (0.5232 to 0.5305), a potential range of Δ(Δ17O) is then about ±0.7 ‰ (C = 0.5305). The ends of this range are not realistic except at very low temperatures (<<0 °C) where values of β become larger and more variable and the lower boundary of κ becomes more obtainable. A more realistic range for equilibrium between natural samples is likely in the vicinity of ±0.3 ‰ (C = 0.5305). This value is comparable to measured values for silica-water fractionation near 0 °C (Sharp et al., 2016
Sharp, Z.D., Gibbons, J.A., Maltsev, O., Atudorei, V., Pack, A., Sengupta, S., Shock, E.L., Knauth, L.P. (2016) A calibration of the triple oxygen isotope fractionation in the Sio2–H2O system and applications to natural samples. Geochimica et Cosmochimica Acta 186, 105-119.
). Kinetic isotope effects should have more variable Δ(Δ17O) values because of their more variable κ values, however the range is expected to be similar to that of equilibrium isotope effects.
Figure 2 Temperature vs. Δ(Δ17O) plot for equilibrium between randomly selected diatomic molecules under the harmonic approximation in the 16O-17O-18O system. A C value of 0.5305 (HTL) is used for the Δ(Δ17O) definition. 1000 ln α18 is plotted as colour. The range of Δ(Δ17O) values in this plot is expected to be an overestimate for natural samples. The points in this model each correspond to a point in Figure 1a.
Regardless of the value of C, Δ(Δ‡M) will approach a high temperature limit of 0 because both β values approach a high temperature limit of 1.000. We recommend the use of the high temperature limit of κ for C which will ensure that the (C-κ) terms in Equation 14 remain positive. For sufficiently different β values (i.e. non-small values of ln α*A-B) the sign of Δ(Δ‡M) will be determined by the larger β. For positive ln α*A-B values, Δ(Δ‡M) will tend to be negative and vice-versa. This trend is not necessarily expected when α is near unity, particularly at low temperatures.
top
Haematite-Water Fractionation
For crossover scenarios, there is a guarantee that the determined α value will be near unity. In Bao and Koch (1999)
Bao, H.M., Koch, P.L. (1999) Oxygen isotope fractionation in ferric oxide-water systems: Low temperature synthesis. Geochimica et Cosmochimica Acta 63, 599-613.
haematite (Fe2O3)-water fractionation was measured over a range of near-surface temperatures. Nine samples are selected from this study for new triple oxygen isotope analysis. Details of the analysis and the tabulated results can be found in the Supplementary Information. The new calculated fractionation parameters with their uncertainties and best fits are illustrated in Figure 3.
Figure 3 Three isotope fractionation parameters for haematite synthesis conducted by Bao and Koch (1999)
Bao, H.M., Koch, P.L. (1999) Oxygen isotope fractionation in ferric oxide-water systems: Low temperature synthesis. Geochimica et Cosmochimica Acta 63, 599-613.
. Values are calculated from newly measured δ18Ohaematite and δ18Owater values, and an assumed Δ17O (C = 0.528) of 0.02 ‰ for the water based on reported Baltimore tap water from Li et al. (2015)Li, S.N., Levin, N.E., Chesson, L.A. (2015) Continental scale variation in O-17-excess of meteoric waters in the United States. Geochimica et Cosmochimica Acta 164, 110-126.
. Δ(Δ17O) are reported using C = 0.5305. The method for calculating uncertainties can be found in the Supplementary Information. Best fit curves for the ln (α) values are second order polynomials of 1/T. The best fit curves for Δ(Δ17O) and θ are calculated from the fits to ln (α).From the calculated haematite fractionation parameters, it is clear that the crossover temperature is different for α17 and α18. With one exception, every experimentally measured θ value exists outside of the typical “canonical” range of θ (approximately 0.5000 to 0.5305) to beyond 1 σ uncertainties. Despite the variability in θ, Δ(Δ17O) values remain within a range of -0.026 ‰ to -0.226 ‰ within the theoretically predicted mass dependent range.
top
Conclusions
Using the simplest application of the B-GM-U model, it is shown theoretically that values of the mass fractionation exponent, θ, are unbounded and particularly variable for small fractionations and at low temperatures. This is in contrast to the mass-fractionation exponent, κ, which is bounded by upper and lower limits. As a supplemental mass-fractionation descriptor, Δ(Δ‡M) is suggested on a theoretical basis because it remains within a finite range for mass-dependent fractionations. The haematite-water system at near surface temperatures is cited as an example of deviations from the “canonical” range of θ for oxygen. These deviations are found to be consistent with a finite range of Δ(Δ17O). It is our opinion based on the results of this study that even for elemental processes the concept of a “canonical” range of θ values is not well founded and should be applied with caution.
top
Acknowledgements
Financial support is provided by US NSF grant EAR-1251824, China NSFC grant 41490635 to HB.
Editor: Eric H. Oelkers
top
References
Bao, H., Cao, X., Hayles, J.A. (2015) The confines of triple oxygen isotope exponents in elemental and complex mass-dependent processes. Geochimica et Cosmochimica Acta 170, 39-50.
 Show in context
Show in context The three isotope relationship was recently re-investigated for complex processes by Bao et al. (2015) using a broadly approximate treatment for elemental processes (i.e. equilibrium and kinetic isotope effects).
View in article
Bao, H.M., Koch, P.L. (1999) Oxygen isotope fractionation in ferric oxide-water systems: Low temperature synthesis. Geochimica et Cosmochimica Acta 63, 599-613.
 Show in context
Show in context In Bao and Koch (1999) haematite (Fe2O3)-water fractionation was measured over a range of near-surface temperatures.
View in article
Figure 3 [...] Three isotope fractionation parameters for haematite synthesis conducted by Bao and Koch (1999).
View in article
Bao, H.M., Lyons, J.R., Zhou, C.M. (2008) Triple oxygen isotope evidence for elevated CO2 levels after a Neoproterozoic glaciation. Nature 453, 504-506.
 Show in context
Show in context Multiple stable isotope ratios have, among other uses, found utility as tools to elucidate photochemical (Farquhar et al., 2000; Bao et al., 2008) or magnetic isotope effects (Blum et al., 2014) and as an identifying markers for extraterrestrial materials (Clayton et al., 1973).
View in article
Bigeleisen, J., Mayer, M.G. (1947) Calculation of equilibrium constants for isotopic exchange reactions. Journal of Chemical Physics 15, 261-267.
 Show in context
Show in context The first accurate model for predicting the separation of isotopes for equilibrium processes was published independently by Urey (1947) and Bigeleisen and Goeppert-Mayer (1947; the B-GM-U model).
View in article
Blum, J.D., Sherman, L.S., Johnson, M.W. (2014) Mercury isotopes in Earth and Environmental Sciences. In: Jeanloz, R. (Ed.) Annual Review of Earth and Planetary Sciences. Vol 42. Annual Reviews, Palo Alto, 249-269.
 Show in context
Show in context Multiple stable isotope ratios have, among other uses, found utility as tools to elucidate photochemical (Farquhar et al., 2000; Bao et al., 2008) or magnetic isotope effects (Blum et al., 2014) and as an identifying markers for extraterrestrial materials (Clayton et al., 1973).
View in article
Cao, X.B., Liu, Y. (2011) Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes. Geochimica et Cosmochimica Acta 75, 7435-7445.
 Show in context
Show in context Analogously to the concept of β, Cao and Liu (2011) first introduced the concept of κ defined as the one species analogue of θ, or 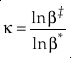 where β is the one species fractionation factor for the two-isotope system.
where β is the one species fractionation factor for the two-isotope system.
View in article
The relationship between κ and θ is given by (Cao and Liu, 2011) 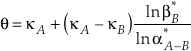
View in article
In this case, the value of κ decreases with increasing mass of the non-substituted atom (Cao and Liu, 2011).
View in article
Clayton, R.N., Grossman, L., Mayeda, T.K. (1973) Component of primitive nuclear composition in carbonaceous meteorites. Science 182, 485-488.
 Show in context
Show in context Multiple stable isotope ratios have, among other uses, found utility as tools to elucidate photochemical (Farquhar et al., 2000; Bao et al., 2008) or magnetic isotope effects (Blum et al., 2014) and as an identifying markers for extraterrestrial materials (Clayton et al., 1973).
View in article
Deines, P. (2003) A note on intra-elemental isotope effects and the interpretation of non-mass-dependent isotope variations. Chemical Geology 199, 179-182.
 Show in context
Show in context Studies investigating these scenarios for sulphur (Deines, 2003; Otake et al., 2008) and hydrogen (Kotaka et al., 1992) have come to the same conclusion.
View in article
Additional evidence against a universal κ - β* relationship can be found in studies implicating crossovers for θ values approaching infinity (Kotaka et al., 1992; Deines, 2003; Otake et al., 2008).
View in article
Eiler, J., Cartigny, P., Hofmann, A.E., Piasecki, A. (2013) Non-canonical mass laws in equilibrium isotopic fractionations: Evidence from the vapor pressure isotope effect of SF6. Geochimica et Cosmochimica Acta 107, 205-219.
 Show in context
Show in context Here, “canonical” refers to a θ value being within certain range represented by most of the observed cases and theoretical justifications (e.g., 0.50-0.5305 for the 16O-17O-18O system; Eiler et al., 2013).
View in article
Farquhar, J., Bao, H.M., Thiemens, M. (2000) Atmospheric influence of Earth's earliest sulfur cycle. Science 289, 756-758.
 Show in context
Show in context Multiple stable isotope ratios have, among other uses, found utility as tools to elucidate photochemical (Farquhar et al., 2000; Bao et al., 2008) or magnetic isotope effects (Blum et al., 2014) and as an identifying markers for extraterrestrial materials (Clayton et al., 1973).
View in article
Kaiser, J., Rockmann, T., Brenninkmeijer, C.A.M. (2004) Contribution of mass-dependent fractionation to the oxygen isotope anomaly of atmospheric nitrous oxide. Journal of Geophysical Research-Atmospheres 109, 11.
 Show in context
Show in context Due to the use of the “low-u” (see Eq. 3) approximation of Equation 2, it was commonly believed that the value of the three isotope exponent was somewhat constant and later thought to be constrained to a finite, “canonical”, range for mass-dependent processes which remains as an accepted idea (Swain et al., 1958; Matsuhisa et al., 1978; Young et al., 2002, 2016; Kaiser et al., 2004).
View in article
Kotaka, M., Okamoto, M., Bigeleisen, J. (1992) Anomalous mass effects in isotopic exchange equilibria. Journal of the American Chemical Society 114, 6436-6445.
 Show in context
Show in context Studies investigating these scenarios for sulphur (Deines, 2003; Otake et al., 2008) and hydrogen (Kotaka et al., 1992) have come to the same conclusion.
View in article
Additional evidence against a universal κ - β* relationship can be found in studies implicating crossovers for θ values approaching infinity (Kotaka et al., 1992; Deines, 2003; Otake et al., 2008).
View in article
Li, S.N., Levin, N.E., Chesson, L.A. (2015) Continental scale variation in O-17-excess of meteoric waters in the United States. Geochimica et Cosmochimica Acta 164, 110-126.
 Show in context
Show in context Figure 3 [...] Values are calculated from newly measured δ18Ohaematite and δ18Owater values, and an assumed Δ17O (C = 0.528) of 0.02 ‰ for the water based on reported Baltimore tap water from Li et al. (2015).
View in article
Matsuhisa, Y., Goldsmith, J.R., Clayton, R.N. (1978) Mechanisms of hydrothermal crystallization of quartz at 250 °C and 15 kbar. Geochimica et Cosmochimica Acta 42, 173-180.
 Show in context
Show in context Due to the use of the “low-u” (see Eq. 3) approximation of Equation 2, it was commonly believed that the value of the three isotope exponent was somewhat constant and later thought to be constrained to a finite, “canonical”, range for mass-dependent processes which remains as an accepted idea (Swain et al., 1958; Matsuhisa et al., 1978; Young et al., 2002, 2016; Kaiser et al., 2004).
View in article
Otake, T., Lasaga, A.C., Ohmoto, H. (2008) Ab initio calculations for equilibrium fractionations in multiple sulfur isotope systems. Chemical Geology 249, 357-376.
 Show in context
Show in context Studies investigating these scenarios for sulphur (Deines, 2003; Otake et al., 2008) and hydrogen (Kotaka et al., 1992) have come to the same conclusion.
View in article
Additional evidence against a universal κ - β* relationship can be found in studies implicating crossovers for θ values approaching infinity (Kotaka et al., 1992; Deines, 2003; Otake et al., 2008).
View in article
Sharp, Z.D., Gibbons, J.A., Maltsev, O., Atudorei, V., Pack, A., Sengupta, S., Shock, E.L., Knauth, L.P. (2016) A calibration of the triple oxygen isotope fractionation in the Sio2–H2O system and applications to natural samples. Geochimica et Cosmochimica Acta 186, 105-119.
 Show in context
Show in context This value is comparable to measured values for silica-water fractionation near 0 °C (Sharp et al., 2016).
View in article
Skaron, S., Wolfsberg, M. (1980) Anomalies in the fractionation by chemical-equilibrium of O-18-O-16 relative to O-17-O-16. Journal of Chemical Physics 72, 6810-6811.
 Show in context
Show in context Using a theoretical framework which represented strictly mass dependent scenarios, Skaron and Wolfsberg (1980) showed theoretically for oxygen isotope partitioning that θ can vary from positive to negative infinity for crossover scenarios, situations where the fractionation factor α for transitions from greater than 1 (heavier isotopes partitioned to A) to less than 1 (heavier isotopes partitioned to B) or vice-versa with changing temperature.
View in article
Swain, C.G., Stivers, E.C., Reuwer, J.F., Schaad, L.J. (1958) Use of hydrogen isotope effects to identify the attacking nucleophile in the enolization of ketones catalyzed by acetic acid. Journal of the American Chemical Society 80, 5885-5893.
 Show in context
Show in context Due to the use of the “low-u” (see Eq. 3) approximation of Equation 2, it was commonly believed that the value of the three isotope exponent was somewhat constant and later thought to be constrained to a finite, “canonical”, range for mass-dependent processes which remains as an accepted idea (Swain et al., 1958; Matsuhisa et al., 1978; Young et al., 2002, 2016; Kaiser et al., 2004).
View in article
Equation 10 is the same as the approximation to the mass fractionation law used by Swain et al. (1958) for triple-hydrogen system.
View in article
Using the arguments of Swain et al. (1958), it is expected that polyatomic molecules will behave within or near the diatomic boundaries of κharm presented here.
View in article
Urey, H.C. (1947) The thermodynamic properties of isotopic substances. Journal of the Chemical Society, 562-581.
 Show in context
Show in context The first accurate model for predicting the separation of isotopes for equilibrium processes was published independently by Urey (1947) and Bigeleisen and Goeppert-Mayer (1947; the B-GM-U model).
View in article
Wolfsberg, M. (1972) Theoretical evaluation of experimentally observed isotope-effects. Accounts of Chemical Research 5, 225.
 Show in context
Show in context The harmonic contribution can be separated into the product of three terms: (a) the Teller-Redlich product rule (TRPR) term; (b) the zero-point energy (ZPE) contribution; and (c) non-zero point energy contributions (EXC) (Wolfsberg, 1972).
View in article
Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095-1104.
 Show in context
Show in context Due to the use of the “low-u” (see Eq. 3) approximation of Equation 2, it was commonly believed that the value of the three isotope exponent was somewhat constant and later thought to be constrained to a finite, “canonical”, range for mass-dependent processes which remains as an accepted idea (Swain et al., 1958; Matsuhisa et al., 1978; Young et al., 2002, 2016; Kaiser et al., 2004).
View in article
Young, E.D., Kohl, I.E., Warren, P.H., Rubie, D.C., Jacobson, S.A., Morbidelli, A. (2016) Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Science 351, 493-496.
 Show in context
Show in context Due to the use of the “low-u” (see Eq. 3) approximation of Equation 2, it was commonly believed that the value of the three isotope exponent was somewhat constant and later thought to be constrained to a finite, “canonical”, range for mass-dependent processes which remains as an accepted idea (Swain et al., 1958; Matsuhisa et al., 1978; Young et al., 2002, 2016; Kaiser et al., 2004).
View in article
top
Supplementary Information
Anharmonic Correction
The harmonic approximation yields the largest contributions to both β and κ for any isotope system. However, for hydrogen bearing molecules, corrections for anharmonicity become significant enough to consider. The complete expression, accounting for anharmonicity, for the vibrational contribution to the energy levels of a diatomic molecule is given by
Eq. S-1
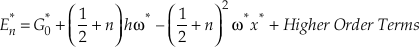
where the second term corresponds to harmonic vibrations (Wolfsberg, 1969). The first and third terms give the anharmonic correction and
Eq. S-2

Eq. S-3
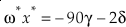
where δ and γ are functions of the parameters of the anharmonic potential, and μ the bond force constant. Because both δ and γ are proportional to 1 / μ, both G0 and ?x are proportional to 1 / μ (Wolfsberg, 1969). The value of κ for the G0 contribution for a diatomic molecule is then simply given by
Eq. S-4
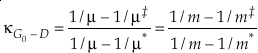
which has a constant value equal to the high-temperature limit for harmonic vibrations. The zero-point energy of the remaining anharmonic term, which gives the majority of the correction, is given by ?x / 4 which yields a κ value also equal to the correction from G0. The constancy of this value, although treated as the complete correction, was originally determined by Cao and Liu (2011). The κ values for the excited state contributions to this term as well as higher order corrections are not calculated here but have respective β values that are expected to be small enough to mostly be neglected for any system.
The effect of anharmonic corrections on the value of κ is treated in the same manner as additional vibrational degrees of freedom so that the final κ value is equal to the sum of the ln β weighted contributions from the anharmonic correction and harmonic κ values. Because the anharmonic corrections are small (<5 % for hydrogen) relative to the harmonic contribution and have a predictable and equal κ value, incorporation of the anharmonic correction yields only a slightly lower value of κ than the harmonic model. Although the small percent change in the value of κ is valid for polyatomic molecules, the value of κ may not necessarily be equal to the harmonic high temperature limit. As a result, incorporation of the anharmonic correction may not strictly decrease κ relative to the harmonic model for polyatomic molecules, but its effect will still be small.
Kinetic Isotope Effects
Kinetic isotope effects can be modelled as equilibrium between the relevant reactant and the transition state with the modification that one degree of freedom for the transition state corresponds to the decomposition mode (Bigeleisen and Wolfsberg, 1958). This can be described as a two mass harmonic oscillator with a negative bond force constant, and hence an imaginary frequency, and is applied by multiplying Equation 2 in the main text (minus one degree of freedom) by the ratio of the imaginary frequencies for the differently substituted states (Bigeleisen and Wolfsberg, 1958). The value of κ for the imaginary frequency contribution is then given by
Eq. S-5
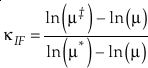
where μ corresponds to the reduced mass of the decomposition fragments. Because the imaginary frequency contribution to β is always less than 1.000, the result of Equation S-5, on average, results in higher values of κ for transition states, but a higher value is not necessarily the case. Because of this, κ for the transition state including the imaginary frequency contribution does not remain bounded by the harmonic limits described above but should remain within or near those boundaries for species with large contributions from other vibrational degrees of freedom. The result is that θ for kinetic isotope effects have a wider distribution than for equilibrium isotope effects. As previous research has shown, normal kinetic isotope effects are expected to exhibit, on average, lower values of θ (Young et al., 2002; Bao et al., 2015). However, we emphasise that kinetic isotope effects should not be strictly associated with low θ values, but rather, more variable θ values.
Experimental Methods
The iron oxide materials used for this study were originaly precipitated for a study by Bao and Koch (1999). The iron oxides were stored as dry powders for nearly a decade and a half in centrifuge tubes since their original precipitation and processing. All processing of the samples apart from the new triple oxygen isotope analysis were conducted for the original study (Bao and Koch, 1999). From the available samples, 9 synthetic haematite samples were selected based on the process used. All selected samples were precipitated from NaOH + HCO3- solutions (molar ratios OH / Fe ≈ 3, HCO3- / Fe ≈ 0.7) at various temperatures for times ranging from 24 hours to 190 days depending on reaction temperature. Samples using this precipitation procedure were chosen because this procedure consistently generated haematite (as opposed to goethite and akaganeite) over the entire temperature range. The samples were then washed in a HCl solution to eliminate amorphous phases and then dried. XRD results for the selected samples show that the samples were pure haematite with the exception of sample CH-19A which may contain trace goethite (Bao and Koch, 1999).
In the 1999 study, haematite samples were converted to O2 by CO2-laser fluorination and analysed for δ18O on a Thermo Finnigan MAT 252 isotope ratio mass spectrometer at the Geophysical Laboratory, Carnegie Institute, Washington. The O2 yields were at or near 100 % for these samples with a precision of ±0.05 ‰ and duplicate analyses being within 0.3 ‰ for δ18O (Bao and Koch, 1999). Water with a known δ18O composition (-8.0 ‰ ± 0.1 ‰) was used for all synthesis solutions. The water that was used is doubly deionised New Jersey tap water. The δ18O of the water was determined by CO2 equlibration on a Micromass Isoprep 18 automated water analysis system interfaced with an Optima isotope ratio mass spectrometer at the Department of Geosciences, Princeton University (Bao and Koch, 1999). Further details, descriptions and notes on the above procedures can be found in Bao and Koch (1999).
New analysis of the haematite samples from Bao and Koch (1999) was conducted at Louisiana State University. Haematite samples were analysed for triple oxygen isotope composition as O2 on a Thermo Finnigan MAT 253 isotope ratio mass spectrometer. Precision of O2 isotope analysis is on the order of 0.03 ‰ or better for both the δ’18O and Δ’17O. Prior to conversion to O2, haematite samples were placed in a 20 torr BrF5 atmosphere overnight to eliminate adsorbed water. Haematite samples were converted to O2 by laser fluorination in a ~20 torr BrF5 atmosphere. The resulting O2 gas was purified using a series of LN2 cooled U-traps before being collected into 5 Å molecular sieve for transfer to the mass spectrometer. The triple oxygen isotope composition of the O2 derived from each haematite sample is initialy measured in dual inlet mode relative to a house standard, LSU-O2 (δ18O = 17.540 ‰; δ17O = 8.84 ‰). The house standard was initially calibrated to VSMOW using O2 gas derived from BrF5 laser fluorination of a dozen of UWG-2 samples using the same procedure described above. The δ18O (5.800 ‰) for UWG-2 is taken from Valley et al. (1995) and an assigned δ17O value of 3.016 ‰. These values give UWG-2, according to our lab reference scale, a Δ’17O (C = 0.5305) of -0.057 ‰ which is between the reported values of -0.019 ‰ and -0.113 ‰ from Young et al. (2016) and Pack and Herwartz (2014, 2015) respectively.
Calculation of Parameters for Haematite Water Fractionation
Values for θ, Δδ’18O (=1000 ‰ ln α 18), Δδ’17O and Δ(Δ’17O) are calculated using the equation
Eq. S-6

Eq. S-7
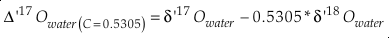
Eq. S-8
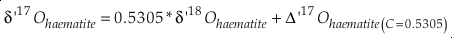
Eq. S-9
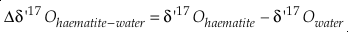
Eq. S-10
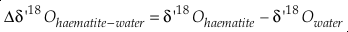
Eq. S-11
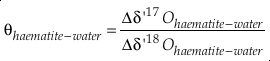
and
Eq. S-12
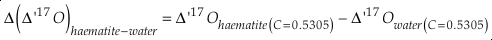
Uncertainties for each fractionation parameter are calculated using a Monte Carlo method. The method uses the above equations, inputs for each known parameter and their respective 1 σ uncertainties. These input uncertainties include those for the new haematite δ’18O and Δ’17O measurements (±0.03 ‰), the uncertainty of the original water δ18O measurement (±0.1 ‰) and an assumed uncertainty of the Δ17O of the water used for precipitation (±0.02 ‰; C = 0.528). The uncertainty for the Δ17O of the water was chosen so that nearly all reported values for the Δ17O for tap waters in the continental United States lie within 1 σ of the central value (Li et al., 2015). A distribution of 1000 values are generated for each parameter with the same statistics as the respective parameter. These values are then processed through Equations S-6 through S-12 and the mean and standard deviation are calculated for the results. The distributions for Δδ17O, Δδ18O and Δ(Δ17O) are found to be normal in all cases, but the distributions of θ are slightly skewed. For θ, the central value is the median and the uncertainties correspond to the 84.1 % and 15.9 % quantiles giving the boundaries of the central 68.2 % of the distribution. The median is chosen, as opposed to the mean for θ, because it gives the same result as the solution using only the central values of the inputs. As a caveat, the results of the calculated haematite-water fractionation parameters given here assume that the calibrations of Li et al. (2015) and Bao and Koch (1999) for water isotope analysis are consistent with our calibration. Slight differences in calibration to SMOW/VSMOW between studies may have an effect on the calculated values of each parameter but this is not expected to be significant for the range of θ values.
Computational Methods
We utilise a Monte Carlo approach to provide a visual representation of the results of this study (Main Text, Figs. 1 and 2). The Monte Carlo models use the diatomic special case for ease of calculation because the vibrational frequency can be simply described as a function of the bond force constant and reduced mass. The model uses 1,000,000 evenly distributed randomly generated values for the secondary mass (0-300 AMU), the bond force constant (0-kUL), and temperature (200-1600 °K). The bond force constant for carbon monoxide (CO) is used as an arbitrary upper limit (UL) for the bond force constant for diatomic oxygen species. All calculations were performed in R (R Core Team, 2012).
Tabulated Oxygen Isotope Results for Haematite Precipitation
Table S-1 Results from both previous δ18O (converted to logarithmic definition) measurements from Bao and Koch (1999) and new δ’18O and Δ17O analysis from this study. δ'17O values for the water are calculated using the δ’18O values for the water measured by Bao and Koch (1999) and published Δ17O values for Baltimore tap water (Li et al., 2015). Values of α are for haematite precipitation with oxygen sourced from water (αhaematite-water). The method for determining uncertainties is described in the text of the Supplementary Information. All uncertainties are 1 σ.
| Sample Name | T in K | Previous δ'18O (‰) SMOW | δ'18O (‰) VSMOW | δ'17O (‰) VSMOW | Δ17O (‰) VSMOW | 1000 ln (α18) | 1000 ln (α17) | θ | Δ(Δ17O) (‰) VSMOW |
| CH-20A | 303.15 | -6.9239 | -6.1482 | -3.369 | -0.1074 | 1.8828 ± 0.1067 | 0.8513 ± 0.0653 | 0.4525 (+0.0197; -0.0207) | -0.1475 ± 0.0398 |
| CH-20B | 303.15 | -6.9239 | -6.3531 | -3.4352 | -0.0649 | 1.6778 ± 0.1067 | 0.785 ± 0.0653 | 0.468 (+0.0226; -0.0226) | -0.105 ± 0.0398 |
| CH-19A | 310.15 | -7.7298 | -6.8148 | -3.6828 | -0.0675 | 1.2161 ± 0.1067 | 0.5375 ± 0.0653 | 0.4428 (+0.0302; -0.033) | -0.1077 ± 0.0398 |
| CG-13A | 323.15 | -7.8305 | -7.1179 | -3.8504 | -0.0743 | 0.913 ± 0.1067 | 0.3699 ± 0.0653 | 0.4067 (+0.0409; -0.0462) | -0.1145 ± 0.0398 |
| CG-13B | 323.15 | -7.8305 | -6.9974 | -3.7403 | -0.0282 | 1.0335 ± 0.1067 | 0.4799 ± 0.0653 | 0.465 (+0.0361; -0.038) | -0.0683 ± 0.0398 |
| CG-12B | 343.15 | -8.5363 | -8.6214 | -4.5597 | 0.0139 | -0.5904 ± 0.1067 | -0.3394 ± 0.0653 | 0.5761 (+0.0689; -0.065) | -0.0262 ± 0.0398 |
| CH-15A | 368.15 | -9.9493 | -9.8669 | -5.2947 | -0.0603 | -1.8359 ± 0.1067 | -1.0744 ± 0.0653 | 0.5859 (+0.0212; -0.0225) | -0.1004 ± 0.0398 |
| CH-17A | 388.15 | -10.2524 | -10.0992 | -5.5437 | -0.1861 | -2.0682 ± 0.1067 | -1.3234 ± 0.0653 | 0.6404 (+0.02; -0.0207) | -0.2262 ± 0.0398 |
| CH-16A | 413.15 | -10.5555 | -10.9575 | -5.8772 | -0.0643 | -2.9265 ± 0.1067 | -1.657 ± 0.0653 | 0.5664 (+0.0131; -0.0136) | -0.1044 ± 0.0398 |
Supplementary Information References
Bao, H.M., Koch, P.L. (1999) Oxygen isotope fractionation in ferric oxide-water systems: Low temperature synthesis. Geochimica et Cosmochimica Acta 63, 599-613.
Bao, H., Cao, X., Hayles, J.A. (2015) The confines of triple oxygen isotope exponents in elemental and complex mass-dependent processes. Geochimica et Cosmochimica Acta 170, 39-50.
Bigeleisen, J., Wolfsberg, M. (1958) Theoretical and experimental aspects of isotope effects in chemical kinetics. Advances in Chemical Physics 1, 15-76.
Cao, X.B., Liu, Y. (2011) Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes. Geochimica et Cosmochimica Acta 75, 7435-7445.
Levin, N.E., Raub, T.D., Dauphas, N., Eiler, J.M. (2014) Triple oxygen isotope variations in sedimentary rocks. Geochimica et Cosmochimica Acta 139, 173-189.
Li, S.N., Levin, N.E., Chesson, L.A. (2015) Continental scale variation in O-17-excess of meteoric waters in the United States. Geochimica et Cosmochimica Acta 164, 110-126.
Pack, A., Herwartz, D. (2014) The triple oxygen isotope composition of the Earth mantle and understanding delta O-17 variations in terrestrial rocks and minerals. Earth and Planetary Science Letters 390, 138-145.
Pack, A., Herwartz, D. (2015) Observation and interpretation of delta O-17 variations in terrestrial rocks - Response to the comment by Miller et al. on the paper by Pack & Herwartz (2014). Earth and Planetary Science Letters 418, 184-186.
R Core Team (2012) R: A language and environment for statistical computing. R Foundation For Statistical Computing.
Tanaka, R., Nakamura, E. (2013) Determination of 17O-excess of terrestrial silicate/oxide minerals with respect to Vienna Standard Mean Ocean Water (VSMOW). Rapid Communications in Mass Spectrometry 27, 285-297.
Valley, J.W., Kitchen, N., Kohn, M.J., Niendorf, C.R., Spicuzza, M.J. (1995) UWG-2, a garnet standard for oxygen isotope ratios: Strategies for high precision and accuracy with laser heating. Geochimica et Cosmochimica Acta 59, 5223-5231.
Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095-1104.
Young, E.D., Kohl, I.E., Warren, P.H., Rubie, D.C., Jacobson, S.A., Morbidelli, A. (2016) Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Science 351, 493-496.
Wolfsberg, M. (1969) Correction to effect of anharmonicity on isotopic exchange equilibria. Advances in Chemistry Series 89, 185-191.
Figures and Tables
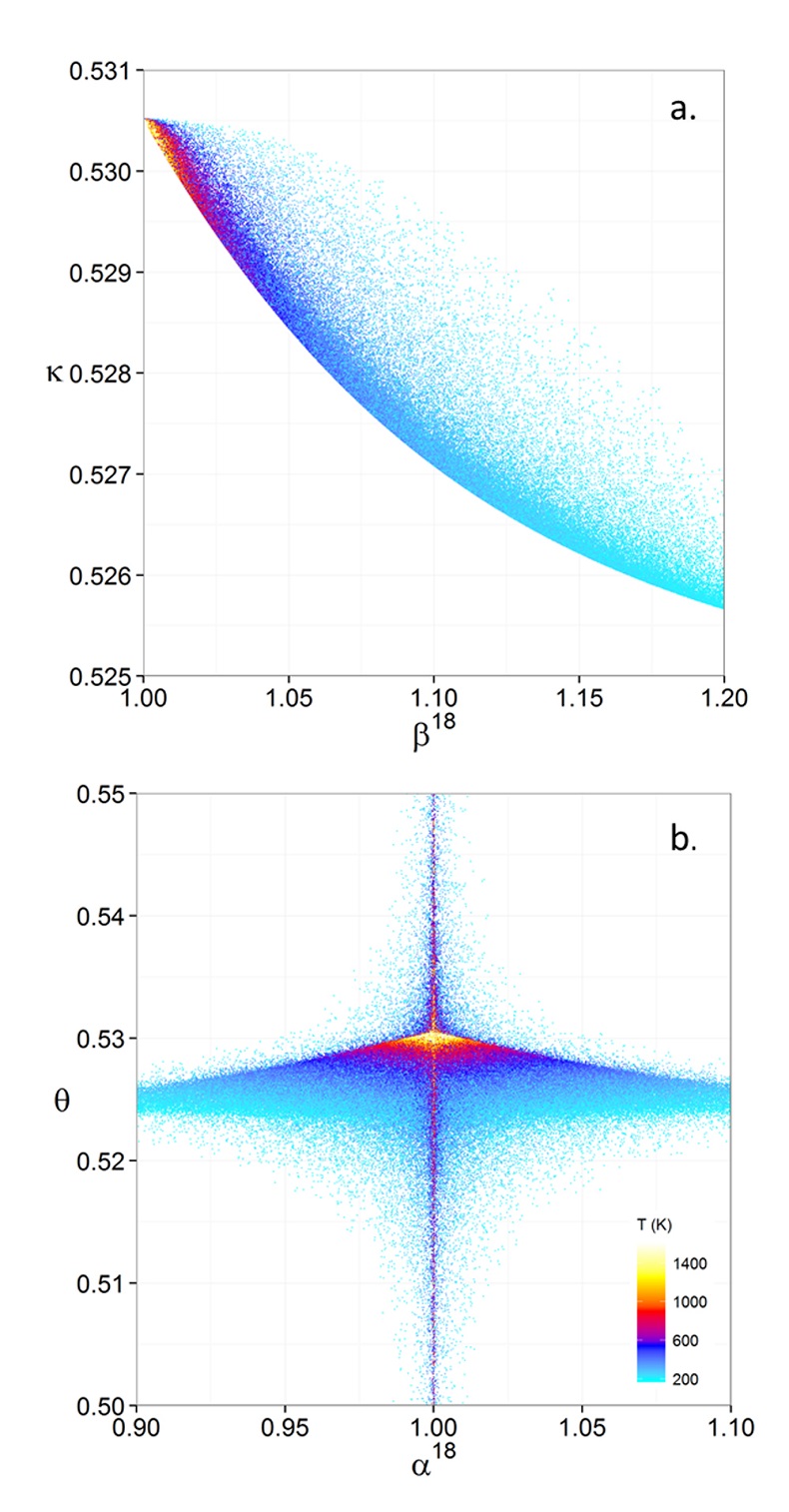
Figure 1 (a) β18 vs. κ and (b) Equilibrium α18 vs. θ plots for randomly selected hypothetical diatomic molecules under the harmonic approximation in the 16O-17O-18O system. Temperature is plotted as colour on the same scale for both plots. The model uses 1,000,000 evenly distributed randomly generated values for the secondary mass (0-300 AMU), the bond force constant (0-kUL), and temperature (200-1600 oK). The bond force constant for carbon monoxide (CO) is used as an arbitrary upper limit (UL) for the bond force constant for diatomic oxygen species.

Figure 2 Temperature vs. Δ(Δ17O) plot for equilibrium between randomly selected diatomic molecules under the harmonic approximation in the 16O-17O-18O system. A C value of 0.5305 (HTL) is used for the Δ(Δ17O) definition. 1000 ln α18 is plotted as colour. The range of Δ(Δ17O) values in this plot is expected to be an overestimate for natural samples. The points in this model each correspond to a point in Figure 1a.
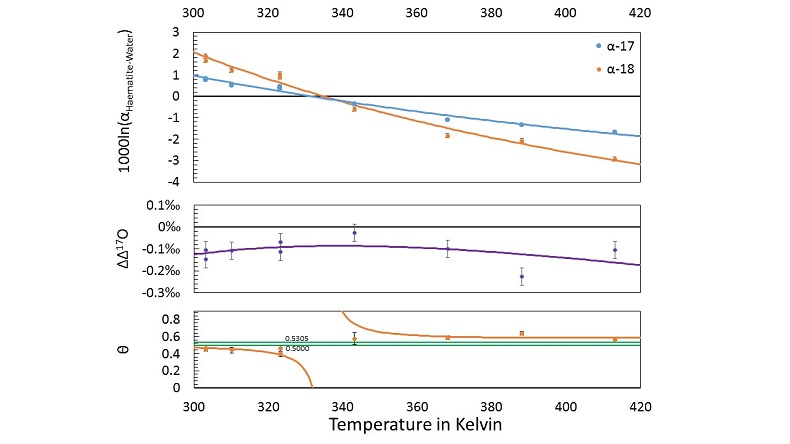
Figure 3 Three isotope fractionation parameters for haematite synthesis conducted by Bao and Koch (1999)
Bao, H.M., Koch, P.L. (1999) Oxygen isotope fractionation in ferric oxide-water systems: Low temperature synthesis. Geochimica et Cosmochimica Acta 63, 599-613.
. Values are calculated from newly measured δ18Ohaematite and δ18Owater values, and an assumed Δ17O (C = 0.528) of 0.02 ‰ for the water based on reported Baltimore tap water from Li et al. (2015)Li, S.N., Levin, N.E., Chesson, L.A. (2015) Continental scale variation in O-17-excess of meteoric waters in the United States. Geochimica et Cosmochimica Acta 164, 110-126.
. Δ(Δ17O) are reported using C = 0.5305. The method for calculating uncertainties can be found in the Supplementary Information. Best fit curves for the ln (α) values are second order polynomials of 1/T. The best fit curves for Δ(Δ17O) and θ are calculated from the fits to ln (α).Supplementary Figures and Tables
Table S-1 Results from both previous δ18O (converted to logarithmic definition) measurements from Bao and Koch (1999) and new δ’18O and Δ17O analysis from this study. δ'17O values for the water are calculated using the δ’18O values for the water measured by Bao and Koch (1999) and published Δ17O values for Baltimore tap water (Li et al., 2015). Values of α are for haematite precipitation with oxygen sourced from water (αhaematite-water). The method for determining uncertainties is described in the text of the Supplementary Information. All uncertainties are 1 σ.
| Sample Name | T in K | Previous δ'18O (‰) SMOW | δ'18O (‰) VSMOW | δ'17O (‰) VSMOW | Δ17O (‰) VSMOW | 1000 ln (α18) | 1000 ln (α17) | θ | Δ(Δ17O) (‰) VSMOW |
| CH-20A | 303.15 | -6.9239 | -6.1482 | -3.369 | -0.1074 | 1.8828 ± 0.1067 | 0.8513 ± 0.0653 | 0.4525 (+0.0197; -0.0207) | -0.1475 ± 0.0398 |
| CH-20B | 303.15 | -6.9239 | -6.3531 | -3.4352 | -0.0649 | 1.6778 ± 0.1067 | 0.785 ± 0.0653 | 0.468 (+0.0226; -0.0226) | -0.105 ± 0.0398 |
| CH-19A | 310.15 | -7.7298 | -6.8148 | -3.6828 | -0.0675 | 1.2161 ± 0.1067 | 0.5375 ± 0.0653 | 0.4428 (+0.0302; -0.033) | -0.1077 ± 0.0398 |
| CG-13A | 323.15 | -7.8305 | -7.1179 | -3.8504 | -0.0743 | 0.913 ± 0.1067 | 0.3699 ± 0.0653 | 0.4067 (+0.0409; -0.0462) | -0.1145 ± 0.0398 |
| CG-13B | 323.15 | -7.8305 | -6.9974 | -3.7403 | -0.0282 | 1.0335 ± 0.1067 | 0.4799 ± 0.0653 | 0.465 (+0.0361; -0.038) | -0.0683 ± 0.0398 |
| CG-12B | 343.15 | -8.5363 | -8.6214 | -4.5597 | 0.0139 | -0.5904 ± 0.1067 | -0.3394 ± 0.0653 | 0.5761 (+0.0689; -0.065) | -0.0262 ± 0.0398 |
| CH-15A | 368.15 | -9.9493 | -9.8669 | -5.2947 | -0.0603 | -1.8359 ± 0.1067 | -1.0744 ± 0.0653 | 0.5859 (+0.0212; -0.0225) | -0.1004 ± 0.0398 |
| CH-17A | 388.15 | -10.2524 | -10.0992 | -5.5437 | -0.1861 | -2.0682 ± 0.1067 | -1.3234 ± 0.0653 | 0.6404 (+0.02; -0.0207) | -0.2262 ± 0.0398 |
| CH-16A | 413.15 | -10.5555 | -10.9575 | -5.8772 | -0.0643 | -2.9265 ± 0.1067 | -1.657 ± 0.0653 | 0.5664 (+0.0131; -0.0136) | -0.1044 ± 0.0398 |