Global climate stabilisation by chemical weathering during the Hirnantian glaciation
Affiliations | Corresponding Author | Cite as | Funding informationKeywords: silicate weathering, weathering thermostat, mass extinction, Ordovician, carbon cycle
- Share this article





Article views:29,343Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract
Figures and Tables
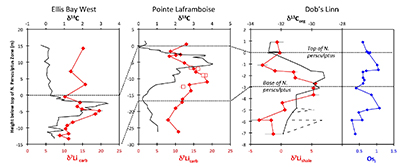 Figure 1 Carbonate (Pointe Laframboise and Ellis Bay West) and shale (Dob’s Linn) Li isotope ratios. Open squares are separately analysed brachiopods. Carbon and osmium (initial 187Os/188Os) isotope data are from the same samples (Finlay et al., 2010). Biostratigraphic correlation is based on the N. persculptus Zone (Melchin et al., 2013). | 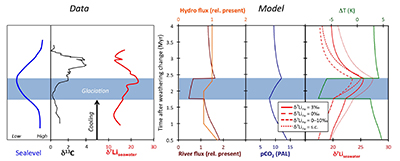 Figure 2 Comparison of data and model results. Sea level timing is from stratigraphic data (Ghienne et al., 2014). Seawater Li isotope data were generated from carbonate data by adding a 4 ‰ fractionation factor (Marriott et al., 2004). The model shows the changes in riverine and hydrothermal Li fluxes, the pCO2 levels and temperature anomalies caused by these changes, and the resulting oceanic δ7Li curve. The red model lines are for scenarios where riverine δ7Li = 3 ‰, 0 ‰, a change from 0 to 10 ‰ during the glaciation and “shale-constrained” (s.c.), using Dob’s Linn δ7Li data to constrain river values (see text and Supplementary Information for detail). |
| Figure 1 | Figure 2 |
Supplementary Figures and Tables
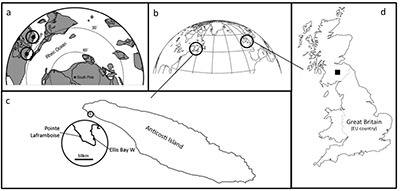 Figure S-1 Sample location maps. (a) Palaeogeographic location map, with sample locations highlighted (adapted from Finlay et al., 2010); (b) Current geography of sample locations from Scotland and Anticosti Island; (c) Detail of sample locations on Anticosti Island; (d) Detail of sample location of Dob’s Linn. |  Table S-1 Li isotope and trace element data from the section studies here. | 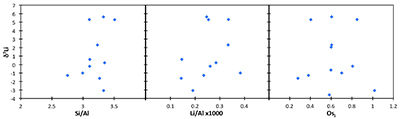 Figure S-2 Lack of correlation between δ7Li and grain size tracer Si/Al, and provenance tracers Li/Al and Os (Osi = 187Os/188Os) isotopes. | 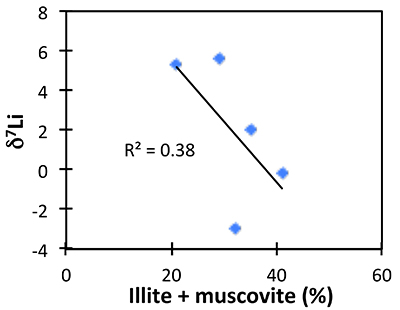 Figure S-3 Lack of significant correlation between shale δ7Li and secondary mineralogy. | 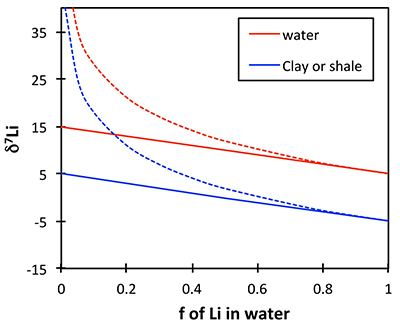 Figure S-4 Example of isotope fractionation behaviour of two linked phases (in this case water and clay) for a constant fractionation factor. Solid lines represent equilibrium fractionation, while dotted lines represent Rayleigh fractionation. |
| Figure S-1 | Table S-1 | Figure S-2 | Figure S-3 | Figure S-4 |
 Table S-2 XRF major element concentration data (in wt. %) for the shales. |  Table S-3 Quantitative mineralogy data from some of the shale samples. |  Table S-4 Results of sequential leaching of some of the Dob’s Linn shales. | 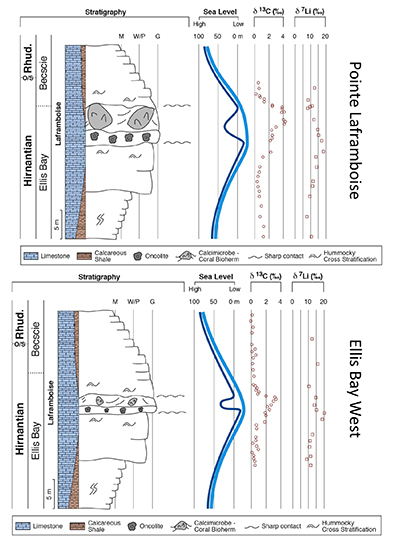 Figure S-5 Anticosti section lithology (Desrochers et al., 2010; Achab et al., 2011, 2013; Copper et al., 2013), compared to isotope data. |  Table S-5 Definitions of parameters used in the models. | 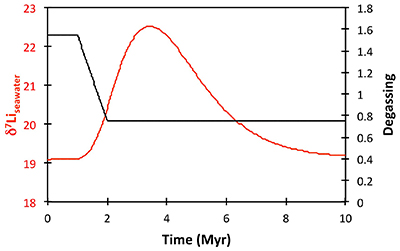 Figure S-6 Result of a permanent decrease in degassing on the Li isotope composition of the oceans. Note that this scenario assumes Rr = 3 ‰. | 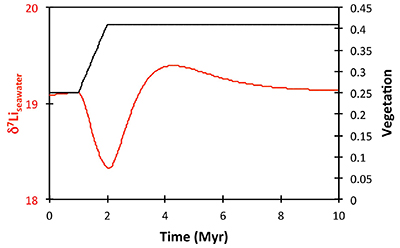 Figure S-7 Result of a permanent increase in vegetation cover on the Li isotope composition of the oceans. Note that this scenario assumes Rr = 3 ‰. |
| Table S-2 | Table S-3 | Table S-4 | Figure S-5 | Table S-5 | Figure S-6 | Figure S-7 |
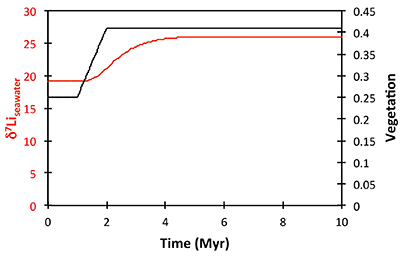 Figure S-8 Result of a permanent increase in vegetation cover combined with an increase in riverine δ7Li on the Li isotope composition of the oceans. | 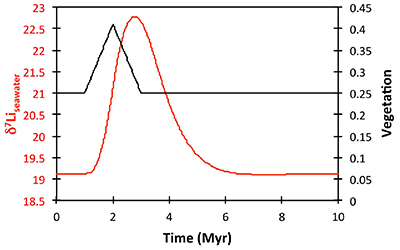 Figure S-9 Identical scenario to Figure S-8 (increase in vegetation cover combined with an increase in riverine δ7Li), but combined with a subsequent decrease in kv and Rr. | 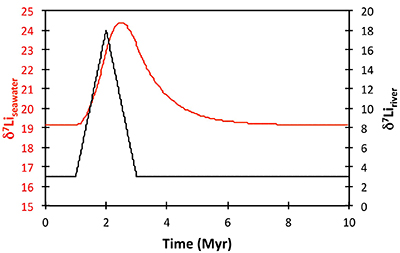 Figure S-10 A scenario where the seawater δ7Li excursion is solely caused by a change in river δ7Li (Rr) (but there is no associated change in the modelled carbon cycle and global temperature). | 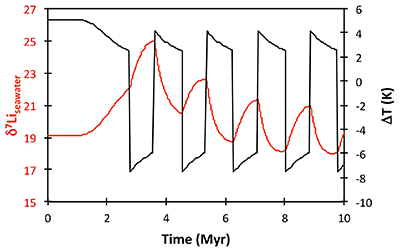 Figure S-11 Effect of an oscillatory system from the feedbacks described in the text on the relative temperature and seawater δ7Li values. | 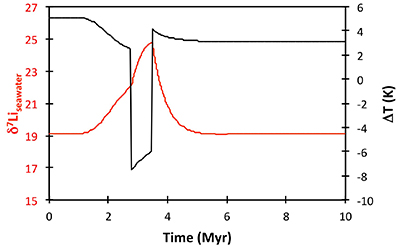 Figure S-12 Effect of single glaciation on the relative temperature and seawater δ7Li values. |
| Figure S-8 | Figure S-9 | Figure S-10 | Figure S-11 | Figure S-12 |
 Figure S-13 The same scenario as in Figure S-12, but with an added temperature control on the fractionation factor of the Li sink. | 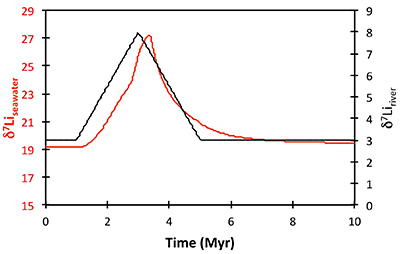 Figure S-14 The same scenario as in Figure S-13, except that riverine δ7Li also increases. | 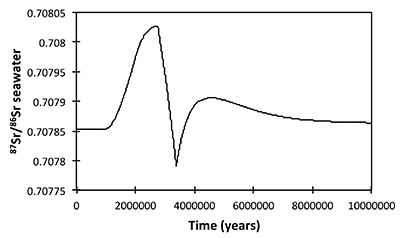 Figure S-15 Modelled Sr isotope ratio of seawater, using factors taken from the Li-C model. |
| Figure S-13 | Figure S-14 | Figure S-15 |
top
Letter
The recovery and stabilisation of Earth’s climate system from perturbations is central to the continued survival of life. Chemical weathering of continental silicate rocks driving marine carbonate precipitation is the Earth’s primary long-term mechanism for removal of atmospheric CO2 (Berner, 2003
Berner, R.A. (2003) The long-term carbon cycle, fossil fuels and atmospheric composition. Nature 426, 323–326.
). A temperature feedback control on weathering rates (i.e. greater temperatures cause higher weathering rates, removing more CO2) would result in a climate-stabilising mechanism. This “weathering thermostat” has long been postulated and assumed in models (Colbourn et al., 2015Colbourn, G., Ridgwell, A., Lenton, T.M. (2015) The time scale of the silicate weathering negative feedback on atmospheric CO2. Global Biogeochemical Cycles 29, 583–596.
). However, direct evidence for weathering rate changes in response to climate perturbations has been harder to pin down in the geological record.The Late Ordovician Hirnantian (~445 Ma) records the second largest mass extinction in Earth history. This was likely caused by rapidly decreasing temperatures, culminating in an ice-sheet over Gondwana (Elrick et al., 2013
Elrick, M., Reardon, D., Labor, W., Martin, J., Desrochers, A., Pope, M. (2013) Orbital-scale climate change and glacioeustasy during the early Late Ordovician (pre-Hirnantian) determined from delta O-18 values in marine apatite. Geology 41, 775–778.
). As such, similarities exist between the Hirnantian and the Late Cenozoic glaciations (Ghienne et al., 2014Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
). The behaviour of atmospheric CO2 is of particular interest, because of the potential role of declining CO2 in initiating the glaciation and of increasing CO2 in terminating it (Vandenbroucke et al., 2010Vandenbroucke, T.R.A., Armstrong, H.A., Williams, M., Paris, F., Zalasiewicz, J.A., Sabbe, K., Nolvak, J., Challandsa, T.J., Verniers, J., Servais, T. (2010) Polar front shift and atmospheric CO2 during the glacial maximum of the Early Paleozoic Icehouse. Proceedings of the National Academy of Sciences of the United States of America 107, 14983–14986.
). Either or both could have involved changes in silicate weathering rates (Berner, 2003Berner, R.A. (2003) The long-term carbon cycle, fossil fuels and atmospheric composition. Nature 426, 323–326.
). The combination of changes in weathering rates and pCO2 also resulted in a global positive δ13C excursion (HICE) (Lenton et al., 2012Lenton, T.M., Crouch, M., Johson, M., Pires, N., Dolan, L. (2012) First plants cooled the Ordovician. Nature Geoscience 5, 86–89.
; Ghienne et al., 2014Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
). Osmium isotopes have suggested a decline in weathering during the glacial maximum (Finlay et al., 2010Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
). However, Os mainly traces weathering provenance, rather than weathering rates or processes. Lithium isotopes are the only tracer available whose behaviour is solely controlled by silicate weathering processes, and therefore give a unique insight into CO2 drawdown and climate-stabilisation.Lithium isotopes (δ7Li) are not fractionated by biological processes (Pogge von Strandmann et al., 2016
Pogge von Strandmann, P.A.E., Burton, K.W., Opfergelt, S., Eiriksdottir, E.S., Murphy, M.J., Einarsson, A., Gislason, S.R. (2016) The effect of hydrothermal spring weathering processes and primary productivity on lithium isotopes: Lake Myvatn, Iceland. Chemical Geology 445, 4–13.
), and are not affected by carbonate weathering (Dellinger et al., 2015Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., Gorge, C., Alanoca, L., Maurice, L. (2015) Riverine Li isotope fractionation in the Amazon River basin controlled by the weathering regimes. Geochimica et Cosmochimica Acta 164, 71–93.
). The δ7Li of primary silicate rocks defines a narrow range (continental crust ~0.6 ± 0.6 ‰, basalt ~3–5 ‰; Sauzeat et al., 2015Sauzeat, L., Rudnick, R.L., Chauvel, C., Garcon, M., Tang, M. (2015) New perspectives on the Li isotopic composition of the upper continental crust and its weathering signature. Earth and Planetary Science Letters 428, 181–192.
) compared to the high variability in modern rivers (2–44 ‰; Huh et al., 1998Huh, Y., Chan, L.H., Zhang, L., Edmond, J.M. (1998) Lithium and its isotopes in major world rivers: Implications for weathering and the oceanic budget. Geochimica et Cosmochimica Acta 62, 2039–2051.
; Dellinger et al., 2015Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., Gorge, C., Alanoca, L., Maurice, L. (2015) Riverine Li isotope fractionation in the Amazon River basin controlled by the weathering regimes. Geochimica et Cosmochimica Acta 164, 71–93.
; Pogge von Strandmann and Henderson, 2015Pogge von Strandmann, P.A.E., Henderson, G.M. (2015) The Li isotope response to mountain uplift. Geology 43, 67–70.
). Riverine values reflect weathering processes, particularly the extent of preferential uptake of 6Li into secondary minerals (Dellinger et al., 2015Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., Gorge, C., Alanoca, L., Maurice, L. (2015) Riverine Li isotope fractionation in the Amazon River basin controlled by the weathering regimes. Geochimica et Cosmochimica Acta 164, 71–93.
), and therefore reflect “weathering congruency”, defined as the ratio of primary rock dissolution (driving rivers to low, rock-like, δ7Li = congruent dissolution of rock), to secondary mineral formation (driving rivers to high δ7Li; Misra and Froelich, 2012Misra, S., Froelich, P.N. (2012) Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science 335, 818–823.
; Pogge von Strandmann and Henderson, 2015Pogge von Strandmann, P.A.E., Henderson, G.M. (2015) The Li isotope response to mountain uplift. Geology 43, 67–70.
). In modern oceans, rivers (~50 % of the ocean input, with a mean δ7Li ~23 ‰; Huh et al., 1998Huh, Y., Chan, L.H., Zhang, L., Edmond, J.M. (1998) Lithium and its isotopes in major world rivers: Implications for weathering and the oceanic budget. Geochimica et Cosmochimica Acta 62, 2039–2051.
) are combined with mid-ocean ridge hydrothermal solutions (~50 %, with a mean δ7Li ~7 ‰; Chan et al., 1993Chan, L.H., Edmond, J.M., Thompson, G. (1993) A lithium isotope study of hot springs and metabasalts from mid-ocean ridge hydrothermal systems. Journal of Geophysical Research 98, 9653–9659.
). The oceanic sinks are incorporation into low-temperature clays in altered oceanic basalt (AOC) and marine authigenic clays (MAAC), which cumulatively impose an isotopic fractionation of ~15 ‰, driving modern seawater to 31 ‰. Marine carbonates represent a negligible sink for Li, and their isotopic fractionation factor remains approximately constant at ~3–5 ‰, independent of temperature, salinity, or whether the calcite is inorganic or skeletal (Marriott et al., 2004Marriott, C.S., Henderson, G.M., Crompton, R., Staubwasser, M., Shaw, S. (2004) Effect of mineralogy, salinity, and temperature on Li/Ca and Li isotope composition of calcium carbonate. Chemical Geology 212, 5–15.
; Pogge von Strandmann et al., 2013Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
).Here we present δ7Li from bulk carbonates and brachiopods from Anticosti Island, Canada (Achab et al., 2013
Achab, A., Asselin, E., Desrochers, A., Riva, J.F. (2013) The end-Ordovician chitinozoan zones of Anticosti Island, Quebec: Definition and stratigraphic position. Review of Palaeobotany and Palynology 198, 92–109.
) (Pointe Laframboise and Ellis Bay West), and from an equivalent shale section at Dob’s Linn, UK (Finlay et al., 2010Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
; Melchin et al., 2013Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
) (see Supplementary Information for methods and data). The δ7Li values from all sections exhibit a positive excursion of ≤10 ‰ before the HICE (Fig. 1). We rule out effects on carbonate δ7Li by silicate leaching, due to our processing technique (see Supplementary Information). We also rule out diagenesis, because trends and absolute values of δ7Li, δ13C and δ18O (Melchin et al., 2013Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
) are reproduced in different sections, both bulk carbonates and brachiopods (Fig. 1). Overall, therefore, this suggests that the Li isotopic excursion represents a primary seawater signal.
Figure 1 Carbonate (Pointe Laframboise and Ellis Bay West) and shale (Dob’s Linn) Li isotope ratios. Open squares are separately analysed brachiopods. Carbon and osmium (initial 187Os/188Os) isotope data are from the same samples (Finlay et al., 2010
Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
). Biostratigraphic correlation is based on the N. persculptus Zone (Melchin et al., 2013Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
).While carbonates tend to be the usual seawater archive (e.g., Misra and Froelich, 2012
Misra, S., Froelich, P.N. (2012) Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science 335, 818–823.
; Pogge von Strandmann et al., 2013Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
), silicates have also been investigated (Dellinger et al., 2017Dellinger, M., Bouchez, J., Gaillardet, J., Faure, L., Moureau, J. (2017) Tracing weathering regimes using the lithium isotope composition of detrital sediments. Geology 45, 411–414.
), and sediments older than Ordovician are considered to represent pre-depositional (unaltered by diagenesis) weathering signals (Li et al., 2016Li, S., Gaschnig, R.M., Rudnick, R.L. (2016) Insights into chemical weathering of the upper continental crust from the geochemistry of ancient glacial diamictites. Geochimica et Cosmochimica Acta 176, 96–117.
). Hence, detrital clays (which dominate at Dob’s Linn) should reflect changing local continental weathering conditions (see Supplementary Information and Fig. S-4). Tracers such as Si/Al, Li/Al or 187Os/188Os rule out control by changing provenance or clay mineralogy. Dob’s Linn exhibits an isotope excursion of similar magnitude, but ~14 ‰ lower than the carbonates. While biostratigraphy suggests that the δ13Ccarb and δ13Corg of Anticosti and Dob’s Linn are slightly offset (Melchin et al., 2013Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
) (Fig. 1), in all sections the relative timings of the δ7Li and HICE are similar. Chemostratigraphy therefore suggests the Li isotope excursions occur contemporaneously (see Supplementary Information), consistent with lithium’s long modern ocean residence time (~1 Myr). A simple temperature dependence of the clay fractionation factor during weathering would only cause <1.6 ‰ variation (Li and West, 2014Li, G., West, A.J. (2014) Evolution of Cenozoic seawater lithium isotopes: Coupling of global denudation regime and shifting seawater sinks. Earth and Planetary Science Letters 401, 284–293.
), and is therefore not the cause of the observed variability. Although shales, in particular clay fractionation factors, are under-constrained for a quantitative interpretation in isolation, their comparison to and temporal similarities with carbonates suggests a link. Thus, global seawater compositions (represented by carbonates) appear to be responding to the same driving force as this local archive of continental weathering (represented by shales).The pre- and post-excursion δ7Liseawater values of ~15 ‰ are difficult to achieve in a modern ocean. It is likely that the AOC and MAAC sinks were broadly similar to today (Hazen et al., 2013
Hazen, R.M., Sverjensky, D.A., Azzolini, D., Bish, D.L., Elmore, S.C., Hinnov, L., Milliken, R.E. (2013) Clay mineral evolution. American Mineralogist 98, 2007–2029.
), imparting an isotopic fractionation factor of ~15 ‰, which may be temperature-dependent, as discussed below. We do not consider a “sink-shift” between proportions of MAAC vs. AOC, as proposed for the Cenozoic (Li and West, 2014Li, G., West, A.J. (2014) Evolution of Cenozoic seawater lithium isotopes: Coupling of global denudation regime and shifting seawater sinks. Earth and Planetary Science Letters 401, 284–293.
), because the Hirnantian duration is likely too short (1–2 Myr) for a transient change. Therefore, Li inputs must have had an isotope ratio close to 0 ‰. Assuming a modern-like hydrothermal input, this requires that rivers had δ7Li values essentially unfractionated from the continental crust (modern value ~0 ‰; Sauzeat et al., 2015Sauzeat, L., Rudnick, R.L., Chauvel, C., Garcon, M., Tang, M. (2015) New perspectives on the Li isotopic composition of the upper continental crust and its weathering signature. Earth and Planetary Science Letters 428, 181–192.
). This possibility is supported by δ7Li values of ~2 ‰ for the Amazon river (Dellinger et al., 2015Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., Gorge, C., Alanoca, L., Maurice, L. (2015) Riverine Li isotope fractionation in the Amazon River basin controlled by the weathering regimes. Geochimica et Cosmochimica Acta 164, 71–93.
), and similarly low values during the peak of the Cenomanian-Turonian hyperthermal (Pogge von Strandmann et al., 2013Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
). However, data here imply that Ordovician oceans were isotopically light at steady state. Given that the first non-vascular land plants were only just evolving and colonising the continents in the mid-late Ordovician (with associated organic acid production), it is probable that clay types were different and less abundant (Hazen et al., 2013Hazen, R.M., Sverjensky, D.A., Azzolini, D., Bish, D.L., Elmore, S.C., Hinnov, L., Milliken, R.E. (2013) Clay mineral evolution. American Mineralogist 98, 2007–2029.
). For example, illites, which cause little Li isotope fractionation (Millot and Girard, 2007Millot, R., Girard, J.P. (2007) Lithium Isotope Fractionation during adsorption onto mineral surfaces. International Meeting: Clays in Natural & Engineered Barriers for Radioactive Waste Confinement (Lille, France).
), are thought to dominate prior to terrestrialisation by plants (Hazen et al., 2013Hazen, R.M., Sverjensky, D.A., Azzolini, D., Bish, D.L., Elmore, S.C., Hinnov, L., Milliken, R.E. (2013) Clay mineral evolution. American Mineralogist 98, 2007–2029.
). If this is a feature of early Earth weathering, then the continental crust’s δ7Li would have been mantle-like (~3 ‰), rather than driven isotopically light by weathering.Assuming, therefore, that silicate weathering was highly congruent, we have created a dynamic non-steady state coupled Li and C cycle model (see Supplementary Information). In brief, the model uses Li formulations from previous work (Pogge von Strandmann et al., 2013
Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
; Lechler et al., 2015Lechler, M., Pogge von Strandmann, P.A.E., Jenkyns, H.C., Prosser, G., Parente, M. (2015) Lithium-isotope evidence for enhanced silicate weathering during OAE 1a (Early Aptian Selli event). Earth and Planetary Science Letters 432, 210–222.
), with an added temperature dependence on the Li sink with a sensitivity of -0.15 ‰/K (Li and West, 2014Li, G., West, A.J. (2014) Evolution of Cenozoic seawater lithium isotopes: Coupling of global denudation regime and shifting seawater sinks. Earth and Planetary Science Letters 401, 284–293.
), and links the weathering flux to that calculated by the carbon cycle model (based on GEOCARB III). Existing climate models suggest that pCO2 needed to halve to ~8 PAL (present atmospheric level) to trigger the Hirnantian glaciation (Pohl et al., 2016Pohl, A., Donnadieu, Y., Le Hir, G., Ladant, J.-B., Dumas, C., Alvarez-Solas, J., Vandenbroucke, T.R.A. (2016) Glacial onset predated Late Ordovician climate cooling. Paleoceanography 31, 800–821.
). This could be initiated by a decline in degassing (McKenzie et al., 2016McKenzie, N.R., Horton, B.K., Loomis, S.E., Stockli, D.F., Planavsky, N.J., Lee, C.-T.A. (2016) Continental arc volcanism as the principal driver of icehouse-greenhouse variability. Science 352, 444–447.
), an increase in plant cover (Lenton et al., 2012Lenton, T.M., Crouch, M., Johson, M., Pires, N., Dolan, L. (2012) First plants cooled the Ordovician. Nature Geoscience 5, 86–89.
) or uplift (Kump et al., 1999Kump, L.R., Arthur, M.A., Patzkowsky, M.E., Gibbs, M.T., Pinkus, D.S., Sheehan, P.M. (1999) A weathering hypothesis for glaciation at high atmospheric pCO2 during the Late Ordovician. Palaeogeography, Palaeoclimatology, Palaeoecology 152, 173–187.
), or a combination of these. A rather extreme decline in degassing from the initial Ordovician value of 1.55× to 0.75× modern causes CO2 to drop to ~6.5 PAL. Both the hydrothermal and riverine Li fluxes scale proportionally to degassing, resulting in no steady state change, but a transient adjustment of the oceanic Li reservoir causes a positive δ7Li excursion of ~3.5 ‰ (i.e. correct direction, but smaller excursion). In contrast, increasing plant-induced weathering (and associated clay mineral formation) causes a permanent, rather than transient δ7Li increase (see Supplementary Information), which is not observed in our data. However, it is possible that the two processes operated in conjunction. A 65 % increase in uplift would create the same effect, but would be unprecedented in the Phanerozoic. Theoretically, the excursion could also be caused by an increase in riverine δ7Li by ~15 ‰ with no change in flux. However this is unlikely, because it implies greater uptake into clay minerals, which would cause a decrease in river flux. This scenario also has no carbon cycle forcing, and hence we prefer a coupled flux and isotope ratio change, initiated by a degassing change.A recent insight is that a glacial “tipping point” existed in the Late Ordovician, where, once global temperature dropped to a critical threshold, northern high latitude sea-ice expanded abruptly, causing a further decrease in global temperatures and rapid expansion of an ice sheet on the Southern polar land surfaces (Pohl et al., 2016
Pohl, A., Donnadieu, Y., Le Hir, G., Ladant, J.-B., Dumas, C., Alvarez-Solas, J., Vandenbroucke, T.R.A. (2016) Glacial onset predated Late Ordovician climate cooling. Paleoceanography 31, 800–821.
). These ice albedo and heat transport feedbacks operate far faster than the long-term carbon cycle. Hence to represent this we implement an abrupt cooling when CO2 reaches ~8 PAL, generating reduced silicate weathering rates. To prevent an immediate abrupt warming, we assume some bi-stability of temperature and ice cover such that CO2 has to rise to >8 PAL before deglaciation occurs. The cooling-induced reduction in global weathering flux (by ~4×), causes an accelerated rise in δ7Li from 17–19 ‰ (depending on continental crust composition) to >25 ‰ (Fig. 2), which is reversed when the build-up of CO2 triggers abrupt warming and deglaciation. Hence peak δ7Li is predicted to be at the end of the glacial interval, consistent with sea-level reconstructions (Fig. 2). The size of the excursion could be increased by coupling the weathering decline with higher riverine δ7Li, as suggested by the shale record (Fig. 2). This could be caused by an increase in the continental residence time of water allowing more clay formation, or a temperature-dependent shift in clay mineralogy. Such a change in congruency could also assist a vegetation-accelerated scenario, where terrestrialisation enhanced weathering, but enhanced glacial grinding forced a return to more congruent weathering. Such vegetative forcing would also cause a transient δ7Li excursion (Fig. S-9), albeit one of longer duration, hence we consider this less likely. Critically, the model can explain an increase in δ7Li as cooling starts, but before the full glaciation was initiated, and the highest oceanic δ7Li occurring at the end of the glaciation as observed in the record. 187Os/188Os values (Finlay et al., 2010Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
) agree with this scenario, suggesting inhibition of weathering by cooling (which would also increase CO2; Kump et al., 1999Kump, L.R., Arthur, M.A., Patzkowsky, M.E., Gibbs, M.T., Pinkus, D.S., Sheehan, P.M. (1999) A weathering hypothesis for glaciation at high atmospheric pCO2 during the Late Ordovician. Palaeogeography, Palaeoclimatology, Palaeoecology 152, 173–187.
) and hence a change in provenance focus, coincident with the δ7Li peak. Our model also predicts 87Sr/86Sr variation within the observed scatter (Shields et al., 2003Shields, G.A., Carden, G.A.F., Veizer, J., Meidla, T., Rong, J.-Y., Li, R.-Y. (2003) Sr, C, and O isotope geochemistry of Ordovician brachiopods: A major isotopic event around the Middle-Late Ordovician transition Geochimica et Cosmochimica Acta 67, 2005–2025.
), lending further credence to our interpretation (see Supplementary Information).
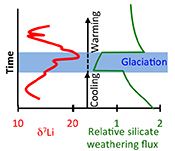
Figure 2 Comparison of data and model results. Sea level timing is from stratigraphic data (Ghienne et al., 2014
Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
). Seawater Li isotope data were generated from carbonate data by adding a 4 ‰ fractionation factor (Marriott et al., 2004Marriott, C.S., Henderson, G.M., Crompton, R., Staubwasser, M., Shaw, S. (2004) Effect of mineralogy, salinity, and temperature on Li/Ca and Li isotope composition of calcium carbonate. Chemical Geology 212, 5–15.
). The model shows the changes in riverine and hydrothermal Li fluxes, the pCO2 levels and temperature anomalies caused by these changes, and the resulting oceanic δ7Li curve. The red model lines are for scenarios where riverine δ7Li = 3 ‰, 0 ‰, a change from 0 to 10 ‰ during the glaciation and “shale-constrained” (s.c.), using Dob’s Linn δ7Li data to constrain river values (see text and Supplementary Information for detail).The data and model are therefore consistent with the Hirnantian glaciation being initiated by declining CO2 degassing, leading to a transient decline in silicate weathering, in turn causing an atmospheric CO2 increase that ultimately terminated the glaciation. The Hirnantian has been compared to Cenozoic glaciations (Ghienne et al., 2014
Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
), where both periods are now characterised by increasing δ7Li values (Misra and Froelich, 2012Misra, S., Froelich, P.N. (2012) Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science 335, 818–823.
). The positive δ7Li excursion during the Hirnantian cooling event also compares well to negative δ7Li excursions during warming events (Pogge von Strandmann et al., 2013Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
; Lechler et al., 2015Lechler, M., Pogge von Strandmann, P.A.E., Jenkyns, H.C., Prosser, G., Parente, M. (2015) Lithium-isotope evidence for enhanced silicate weathering during OAE 1a (Early Aptian Selli event). Earth and Planetary Science Letters 432, 210–222.
). Overall, therefore, this study shows that if a tectonic-driven climate control (degassing) can push the climate system out of balance, a temperature-dependent feedback via silicate weathering will eventually stabilise the climate. Such a weathering thermostat has frequently been postulated as a climate regulating process, but has proven remarkably difficult to unambiguously demonstrate in the geological record.top
Acknowledgements
This study and PPvS were funded by NERC advanced research fellowship NE/I020571/2 and ERC Consolidator grant 682760 - CONTROLPASTCO2. AD thanks the support of the Natural Science and Engineering Council of Canada (Discovery Grant). TML was supported by NERC (NE/N018508/1). DS acknowledges the Total Endowment Fund. Michael Melchin is thanked for reading an earlier version of the manuscript. This manuscript was greatly improved by reviews from Lee Kump, Jerome Gaillardet and an anonymous reviewer.
Editor: Liane G. Benning
top
Author Contributions
PPvS wrote the research proposal, carried out the analyses and wrote the manuscript. TML and PPvS conducted the modelling. AD, AJF and DS provided samples, geochemical context and edited the manuscript. MJM assisted in analyses and edited the manuscript.
top
References
Achab, A., Asselin, E., Desrochers, A., Riva, J.F. (2013) The end-Ordovician chitinozoan zones of Anticosti Island, Quebec: Definition and stratigraphic position. Review of Palaeobotany and Palynology 198, 92–109.
 Show in context
Show in context Here we present δ7Li from bulk carbonates and brachiopods from Anticosti Island, Canada (Achab et al., 2013) (Pointe Laframboise and Ellis Bay West), and from an equivalent shale section at Dob’s Linn, UK (Finlay et al., 2010; Melchin et al., 2013) (see Supplementary Information for methods and data).
View in article
Berner, R.A. (2003) The long-term carbon cycle, fossil fuels and atmospheric composition. Nature 426, 323–326.
 Show in context
Show in context Chemical weathering of continental silicate rocks driving marine carbonate precipitation is the Earth’s primary long-term mechanism for removal of atmospheric CO2 (Berner, 2003).
View in article
Either or both could have involved changes in silicate weathering rates (Berner, 2003).
View in article
Chan, L.H., Edmond, J.M., Thompson, G. (1993) A lithium isotope study of hot springs and metabasalts from mid-ocean ridge hydrothermal systems. Journal of Geophysical Research 98, 9653–9659.
 Show in context
Show in context In modern oceans, rivers (~50 % of the ocean input, with a mean δ7Li ~23 ‰; Huh et al., 1998) are combined with mid-ocean ridge hydrothermal solutions (~50 %, with a mean δ7Li ~7 ‰; Chan et al., 1993).
View in article
Colbourn, G., Ridgwell, A., Lenton, T.M. (2015) The time scale of the silicate weathering negative feedback on atmospheric CO2. Global Biogeochemical Cycles 29, 583–596.
 Show in context
Show in context This “weathering thermostat” has long been postulated and assumed in models (Colbourn et al., 2015).
View in article
Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., Gorge, C., Alanoca, L., Maurice, L. (2015) Riverine Li isotope fractionation in the Amazon River basin controlled by the weathering regimes. Geochimica et Cosmochimica Acta 164, 71–93.
 Show in context
Show in context Lithium isotopes (δ7Li) are not fractionated by biological processes (Pogge von Strandmann et al., 2016), and are not affected by carbonate weathering (Dellinger et al., 2015).
View in article
The δ7Li of primary silicate rocks defines a narrow range (continental crust ~0.6 ± 0.6 ‰, basalt ~3–5 ‰; Sauzeat et al., 2015) compared to the high variability in modern rivers (2–44 ‰; Huh et al., 1998; Dellinger et al., 2015; Pogge von Strandmann and Henderson, 2015).
View in article
Riverine values reflect weathering processes, particularly the extent of preferential uptake of 6Li into secondary minerals (Dellinger et al., 2015), and therefore reflect “weathering congruency”, defined as the ratio of primary rock dissolution (driving rivers to low, rock-like, δ7Li = congruent dissolution of rock), to secondary mineral formation (driving rivers to high δ7Li; Misra and Froelich, 2012; Pogge von Strandmann and Henderson, 2015).
View in article
This possibility is supported by δ7Li values of ~2 ‰ for the Amazon river (Dellinger et al., 2015), and similarly low values during the peak of the Cenomanian-Turonian hyperthermal (Pogge von Strandmann et al., 2013).
View in article
Dellinger, M., Bouchez, J., Gaillardet, J., Faure, L., Moureau, J. (2017) Tracing weathering regimes using the lithium isotope composition of detrital sediments. Geology 45, 411–414.
 Show in context
Show in context While carbonates tend to be the usual seawater archive (e.g., Misra and Froelich, 2012; Pogge von Strandmann et al., 2013), silicates have also been investigated (Dellinger et al., 2017), and sediments older than Ordovician are considered to represent pre-depositional (unaltered by diagenesis) weathering signals (Li et al., 2016).
View in article
Elrick, M., Reardon, D., Labor, W., Martin, J., Desrochers, A., Pope, M. (2013) Orbital-scale climate change and glacioeustasy during the early Late Ordovician (pre-Hirnantian) determined from delta O-18 values in marine apatite. Geology 41, 775–778.
 Show in context
Show in context This was likely caused by rapidly decreasing temperatures, culminating in an ice-sheet over Gondwana (Elrick et al., 2013).
View in article
Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
 Show in context
Show in context Osmium isotopes have suggested a decline in weathering during the glacial maximum (Finlay et al., 2010).
View in article
Here we present δ7Li from bulk carbonates and brachiopods from Anticosti Island, Canada (Achab et al., 2013) (Pointe Laframboise and Ellis Bay West), and from an equivalent shale section at Dob’s Linn, UK (Finlay et al., 2010; Melchin et al., 2013) (see Supplementary Information for methods and data).
View in article
Figure 1 [...] Carbon and osmium (initial 187Os/188Os) isotope data are from the same samples (Finlay et al., 2010).
View in article
187Os/188Os values (Finlay et al., 2010) agree with this scenario, suggesting inhibition of weathering by cooling (which would also increase CO2; Kump et al., 1999) and hence a change in provenance focus, coincident with the δ7Li peak.
View in article
Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
 Show in context
Show in context As such, similarities exist between the Hirnantian and the Late Cenozoic glaciations (Ghienne et al., 2014).
View in article
The combination of changes in weathering rates and pCO2 also resulted in a global positive δ13C excursion (HICE) (Lenton et al., 2012; Ghienne et al., 2014).
View in article
Figure 2 [...] Comparison of data and model results. Sea level timing is from stratigraphic data (Ghienne et al., 2014).
View in article
The Hirnantian has been compared to Cenozoic glaciations (Ghienne et al., 2014), where both periods are now characterised by increasing δ7Li values (Misra and Froelich, 2012).
View in article
Hazen, R.M., Sverjensky, D.A., Azzolini, D., Bish, D.L., Elmore, S.C., Hinnov, L., Milliken, R.E. (2013) Clay mineral evolution. American Mineralogist 98, 2007–2029.
 Show in context
Show in context It is likely that the AOC and MAAC sinks were broadly similar to today (Hazen et al., 2013), imparting an isotopic fractionation factor of ~15 ‰, which may be temperature-dependent, as discussed below.
View in article
Given that the first non-vascular land plants were only just evolving and colonising the continents in the mid-late Ordovician (with associated organic acid production), it is probable that clay types were different and less abundant (Hazen et al., 2013).
View in article
For example, illites, which cause little Li isotope fractionation (Millot and Girard, 2007), are thought to dominate prior to terrestrialisation by plants (Hazen et al., 2013).
View in article
Huh, Y., Chan, L.H., Zhang, L., Edmond, J.M. (1998) Lithium and its isotopes in major world rivers: Implications for weathering and the oceanic budget. Geochimica et Cosmochimica Acta 62, 2039–2051.
 Show in context
Show in context In modern oceans, rivers (~50 % of the ocean input, with a mean δ7Li ~23 ‰; Huh et al., 1998) are combined with mid-ocean ridge hydrothermal solutions (~50 %, with a mean δ7Li ~7 ‰; Chan et al., 1993).
View in article
The δ7Li of primary silicate rocks defines a narrow range (continental crust ~0.6 ± 0.6 ‰, basalt ~3–5 ‰; Sauzeat et al., 2015) compared to the high variability in modern rivers (2–44 ‰; Huh et al., 1998; Dellinger et al., 2015; Pogge von Strandmann and Henderson, 2015).
View in article
Kump, L.R., Arthur, M.A., Patzkowsky, M.E., Gibbs, M.T., Pinkus, D.S., Sheehan, P.M. (1999) A weathering hypothesis for glaciation at high atmospheric pCO2 during the Late Ordovician. Palaeogeography, Palaeoclimatology, Palaeoecology 152, 173–187.
 Show in context
Show in context This could be initiated by a decline in degassing (McKenzie et al., 2016), an increase in plant cover (Lenton et al., 2012) or uplift (Kump et al., 1999), or a combination of these.
View in article
187Os/188Os values (Finlay et al., 2010) agree with this scenario, suggesting inhibition of weathering by cooling (which would also increase CO2; Kump et al., 1999) and hence a change in provenance focus, coincident with the δ7Li peak.
View in article
Lechler, M., Pogge von Strandmann, P.A.E., Jenkyns, H.C., Prosser, G., Parente, M. (2015) Lithium-isotope evidence for enhanced silicate weathering during OAE 1a (Early Aptian Selli event). Earth and Planetary Science Letters 432, 210–222.
 Show in context
Show in context In brief, the model uses Li formulations from previous work (Pogge von Strandmann et al., 2013; Lechler et al., 2015), with an added temperature dependence on the Li sink with a sensitivity of -0.15 ‰/K (Li and West, 2014), and links the weathering flux to that calculated by the carbon cycle model (based on GEOCARB III).
View in article
The positive δ7Li excursion during the Hirnantian cooling event also compares well to negative δ7Li excursions during warming events (Pogge von Strandmann et al., 2013; Lechler et al., 2015).
View in article
Lenton, T.M., Crouch, M., Johson, M., Pires, N., Dolan, L. (2012) First plants cooled the Ordovician. Nature Geoscience 5, 86–89.
 Show in context
Show in context The combination of changes in weathering rates and pCO2 also resulted in a global positive δ13C excursion (HICE) (Lenton et al., 2012; Ghienne et al., 2014).
View in article
This could be initiated by a decline in degassing (McKenzie et al., 2016), an increase in plant cover (Lenton et al., 2012) or uplift (Kump et al., 1999), or a combination of these.
View in article
Li, G., West, A.J. (2014) Evolution of Cenozoic seawater lithium isotopes: Coupling of global denudation regime and shifting seawater sinks. Earth and Planetary Science Letters 401, 284–293.
 Show in context
Show in context A simple temperature dependence of the clay fractionation factor during weathering would only cause <1.6 ‰ variation (Li and West, 2014), and is therefore not the cause of the observed variability.
View in article
We do not consider a “sink-shift” between proportions of MAAC vs. AOC, as proposed for the Cenozoic (Li and West, 2014), because the Hirnantian duration is likely too short (1–2 Myr) for a transient change.
View in article
In brief, the model uses Li formulations from previous work (Pogge von Strandmann et al., 2013; Lechler et al., 2015), with an added temperature dependence on the Li sink with a sensitivity of -0.15 ‰/K (Li and West, 2014), and links the weathering flux to that calculated by the carbon cycle model (based on GEOCARB III).
View in article
Li, S., Gaschnig, R.M., Rudnick, R.L. (2016) Insights into chemical weathering of the upper continental crust from the geochemistry of ancient glacial diamictites. Geochimica et Cosmochimica Acta 176, 96–117.
 Show in context
Show in context While carbonates tend to be the usual seawater archive (e.g., Misra and Froelich, 2012; Pogge von Strandmann et al., 2013), silicates have also been investigated (Dellinger et al., 2017), and sediments older than Ordovician are considered to represent pre-depositional (unaltered by diagenesis) weathering signals (Li et al., 2016).
View in article
Marriott, C.S., Henderson, G.M., Crompton, R., Staubwasser, M., Shaw, S. (2004) Effect of mineralogy, salinity, and temperature on Li/Ca and Li isotope composition of calcium carbonate. Chemical Geology 212, 5–15.
 Show in context
Show in context Marine carbonates represent a negligible sink for Li, and their isotopic fractionation factor remains approximately constant at ~3–5 ‰, independent of temperature, salinity, or whether the calcite is inorganic or skeletal (Marriott et al., 2004; Pogge von Strandmann et al., 2013).
View in article
Figure 2 [...] Seawater Li isotope data were generated from carbonate data by adding a 4 ‰ fractionation factor (Marriott et al., 2004).
View in article
McKenzie, N.R., Horton, B.K., Loomis, S.E., Stockli, D.F., Planavsky, N.J., Lee, C.-T.A. (2016) Continental arc volcanism as the principal driver of icehouse-greenhouse variability. Science 352, 444–447.
 Show in context
Show in context This could be initiated by a decline in degassing (McKenzie et al., 2016), an increase in plant cover (Lenton et al., 2012) or uplift (Kump et al., 1999), or a combination of these.
View in article
Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
 Show in context
Show in context Here we present δ7Li from bulk carbonates and brachiopods from Anticosti Island, Canada (Achab et al., 2013) (Pointe Laframboise and Ellis Bay West), and from an equivalent shale section at Dob’s Linn, UK (Finlay et al., 2010; Melchin et al., 2013) (see Supplementary Information for methods and data).
View in article
We also rule out diagenesis, because trends and absolute values of δ7Li, δ13C and δ18O (Melchin et al., 2013) are reproduced in different sections, both bulk carbonates and brachiopods (Fig. 1).
View in article
Figure 1 [...] Biostratigraphic correlation is based on the N. persculptus Zone (Melchin et al., 2013).
View in article
While biostratigraphy suggests that the δ13Ccarb and δ13Corg of Anticosti and Dob’s Linn are slightly offset (Melchin et al., 2013) (Fig. 1), in all sections the relative timings of the δ7Li and HICE are similar.
View in article
Millot, R., Girard, J.P. (2007) Lithium Isotope Fractionation during adsorption onto mineral surfaces. International Meeting: Clays in Natural & Engineered Barriers for Radioactive Waste Confinement (Lille, France).
 Show in context
Show in context For example, illites, which cause little Li isotope fractionation (Millot and Girard, 2007), are thought to dominate prior to terrestrialisation by plants (Hazen et al., 2013).
View in article
Misra, S., Froelich, P.N. (2012) Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science 335, 818–823.
 Show in context
Show in context Riverine values reflect weathering processes, particularly the extent of preferential uptake of 6Li into secondary minerals (Dellinger et al., 2015), and therefore reflect “weathering congruency”, defined as the ratio of primary rock dissolution (driving rivers to low, rock-like, δ7Li = congruent dissolution of rock), to secondary mineral formation (driving rivers to high δ7Li; Misra and Froelich, 2012; Pogge von Strandmann and Henderson, 2015).
View in article
While carbonates tend to be the usual seawater archive (e.g., Misra and Froelich, 2012; Pogge von Strandmann et al., 2013), silicates have also been investigated (Dellinger et al., 2017), and sediments older than Ordovician are considered to represent pre-depositional (unaltered by diagenesis) weathering signals (Li et al., 2016).
View in article
The Hirnantian has been compared to Cenozoic glaciations (Ghienne et al., 2014), where both periods are now characterised by increasing δ7Li values (Misra and Froelich, 2012).
View in article
Pogge von Strandmann, P.A.E., Henderson, G.M. (2015) The Li isotope response to mountain uplift. Geology 43, 67–70.
 Show in context
Show in context The δ7Li of primary silicate rocks defines a narrow range (continental crust ~0.6 ± 0.6 ‰, basalt ~3–5 ‰; Sauzeat et al., 2015) compared to the high variability in modern rivers (2–44 ‰; Huh et al., 1998; Dellinger et al., 2015; Pogge von Strandmann and Henderson, 2015).
View in article
Riverine values reflect weathering processes, particularly the extent of preferential uptake of 6Li into secondary minerals (Dellinger et al., 2015), and therefore reflect “weathering congruency”, defined as the ratio of primary rock dissolution (driving rivers to low, rock-like, δ7Li = congruent dissolution of rock), to secondary mineral formation (driving rivers to high δ7Li; Misra and Froelich, 2012; Pogge von Strandmann and Henderson, 2015).
View in article
Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
 Show in context
Show in context Marine carbonates represent a negligible sink for Li, and their isotopic fractionation factor remains approximately constant at ~3–5 ‰, independent of temperature, salinity, or whether the calcite is inorganic or skeletal (Marriott et al., 2004; Pogge von Strandmann et al., 2013).
View in article
While carbonates tend to be the usual seawater archive (e.g., Misra and Froelich, 2012; Pogge von Strandmann et al., 2013), silicates have also been investigated (Dellinger et al., 2017), and sediments older than Ordovician are considered to represent pre-depositional (unaltered by diagenesis) weathering signals (Li et al., 2016).
View in article
This possibility is supported by δ7Li values of ~2 ‰ for the Amazon river (Dellinger et al., 2015), and similarly low values during the peak of the Cenomanian-Turonian hyperthermal (Pogge von Strandmann et al., 2013).
View in article
In brief, the model uses Li formulations from previous work (Pogge von Strandmann et al., 2013; Lechler et al., 2015), with an added temperature dependence on the Li sink with a sensitivity of -0.15 ‰/K (Li and West, 2014), and links the weathering flux to that calculated by the carbon cycle model (based on GEOCARB III).
View in article
The positive δ7Li excursion during the Hirnantian cooling event also compares well to negative δ7Li excursions during warming events (Pogge von Strandmann et al., 2013; Lechler et al., 2015).
View in article
Pogge von Strandmann, P.A.E., Burton, K.W., Opfergelt, S., Eiriksdottir, E.S., Murphy, M.J., Einarsson, A., Gislason, S.R. (2016) The effect of hydrothermal spring weathering processes and primary productivity on lithium isotopes: Lake Myvatn, Iceland. Chemical Geology 445, 4–13.
 Show in context
Show in context Lithium isotopes (δ7Li) are not fractionated by biological processes (Pogge von Strandmann et al., 2016), and are not affected by carbonate weathering (Dellinger et al., 2015).
View in article
Pohl, A., Donnadieu, Y., Le Hir, G., Ladant, J.-B., Dumas, C., Alvarez-Solas, J., Vandenbroucke, T.R.A. (2016) Glacial onset predated Late Ordovician climate cooling. Paleoceanography 31, 800–821.
 Show in context
Show in context Existing climate models suggest that pCO2 needed to halve to ~8 PAL (present atmospheric level) to trigger the Hirnantian glaciation (Pohl et al., 2016).
View in article
A recent insight is that a glacial “tipping point” existed in the Late Ordovician, where, once global temperature dropped to a critical threshold, northern high latitude sea-ice expanded abruptly, causing a further decrease in global temperatures and rapid expansion of an ice sheet on the Southern polar land surfaces (Pohl et al., 2016).
View in article
Sauzeat, L., Rudnick, R.L., Chauvel, C., Garcon, M., Tang, M. (2015) New perspectives on the Li isotopic composition of the upper continental crust and its weathering signature. Earth and Planetary Science Letters 428, 181–192.
 Show in context
Show in context The δ7Li of primary silicate rocks defines a narrow range (continental crust ~0.6 ± 0.6 ‰, basalt ~3–5 ‰; Sauzeat et al., 2015) compared to the high variability in modern rivers (2–44 ‰; Huh et al., 1998; Dellinger et al., 2015; Pogge von Strandmann and Henderson, 2015).
View in article
Assuming a modern-like hydrothermal input, this requires that rivers had δ7Li values essentially unfractionated from the continental crust (modern value ~0 ‰; Sauzeat et al., 2015).
View in article
Shields, G.A., Carden, G.A.F., Veizer, J., Meidla, T., Rong, J.-Y., Li, R.-Y. (2003) Sr, C, and O isotope geochemistry of Ordovician brachiopods: A major isotopic event around the Middle-Late Ordovician transition Geochimica et Cosmochimica Acta 67, 2005–2025.
 Show in context
Show in context Our model also predicts 87Sr/86Sr variation within the observed scatter (Shields et al., 2003), lending further credence to our interpretation (see Supplementary Information).
View in article
Vandenbroucke, T.R.A., Armstrong, H.A., Williams, M., Paris, F., Zalasiewicz, J.A., Sabbe, K., Nolvak, J., Challandsa, T.J., Verniers, J., Servais, T. (2010) Polar front shift and atmospheric CO2 during the glacial maximum of the Early Paleozoic Icehouse. Proceedings of the National Academy of Sciences of the United States of America 107, 14983–14986.
 Show in context
Show in context The behaviour of atmospheric CO2 is of particular interest, because of the potential role of declining CO2 in initiating the glaciation and of increasing CO2 in terminating it (Vandenbroucke et al., 2010).
View in article
top
Supplementary Information
Sample Description and Location
Two bulk carbonate sections in the upper Ellis Bay Formation were analysed from the western end of Anticosti Island, Canada. The sections are at Pointe Laframboise (Achab et al., 2011, 2013) and Ellis Bay West (Desrochers et al., 2010), and are separated by just under 10 km (Fig. S-1). The 80-90 m thick Ellis Bay Formation at the west end of Anticosti Island constitutes a comprehensive Hirnantian record of shallow water tropical carbonate (Desrochers et al., 2010; Achab et al., 2011, 2013). Mid- to outer ramp carbonate facies that prevail in the western part of Anticosti Island grade eastward towards the basin margin into thinner, more siliciclastic-rich inner to proximal mid-ramp facies that include several local discontinuities (Desrochers et al., 2010; Achab et al., 2011, 2013). Oncolitic limestones associated with local reef development are present along the entire outcrop belt in the uppermost Laframboise Member of the Ellis Bay Formation. The lithostratigraphic framework of the latest Ordovician strata exposed on Anticosti Island was recently revised (Copper et al., 2013). From the base of the Ellis Bay Formation to the base of the uppermost Laframboise Member at the west end of the island, three chitinozoan zones are distinguished in ascending order: the florentini‐concinna Zone, the gamachiana Zone and the taugourdeaui Zone (Achab et al., 2011, 2013). These zones are all considered Hirnantian in age, based on several concordant palaeontological data related to the occurrence of pre- and post-extinction Hirnantian biota. The Hirnantian age of the Ellis Bay Formation confirms that the Hirnantian isotopic carbon excursion (HICE) is not restricted to the main peak in the Laframboise Member, but includes the smaller excursions in the lower part of the formation and in the uppermost part of the Vaureal Formation. The δ13C drops to pre-excursion values in the A. ellisbayensis chitinozoan zone at the very base of the Becscie Formation during the uppermost N. persculptus Zone (Achab et al., 2011, 2013).
In addition to bulk carbonate analyses, a number of individual large (cm-size) brachiopod fossils were analysed from various points in the Pointe Laframboise section, to assess alteration of bulk carbonates against that of macrofossils.
These Canadian sections were compared with a section from Dob’s Linn, UK (Fig. S-1). Dob’s Linn is the GSSP (Global Boundary Stratotype Section and Point) for the Ordovician-Silurian boundary (Williams, 1983, 1986, 1988).
The sampled section consists of two different shale units of the Moffat Shale Group: the organic-poor (TOC ~ 0.1 %; Finlay et al., 2010) Upper Hartfell Shale, and the organic-rich (TOC ~ 1.5 %; Finlay et al., 2010) Lower Birkhill Shale, which lies above the former. The environment of deposition was a distal micro-turbidite that was deposited on the eastern continental margin of Laurentia during the closure of the Iapetus Ocean (Armstrong and Owen, 2002a,b). Despite containing low TOC values, the Upper Hartfell shale contains several black shale bands (TOC ~ 1–2 %; Finlay et al., 2010). These black bands, and the organic rich Lower Birkhill shale contain numerous graptolites enabling a detailed biostratigraphy of the section to be established (Lapworth, 1878; Melchin et al., 2013). Samples in this study range from the Ordovician complexus to Silurian ascensus Biozones. Furthermore, Dob’s Linn has been previously studied for carbon isotope analysis which confirmed the chronostratigraphic correlation of the section at Dob’s Linn with that of Anticosti Island (Underwood et al., 1997). This enabled Finlay et al. (2010) to analyse their newly collected samples for δ13C and to ensure the stratigraphy of their newly collected samples was correct.
The samples analysed here are the same as used for the Os isotope record presented by Finlay et al. (2010). As shown in that study, there is a small fault around 50 cm below the GSSP, with a likely loss of ~15 cm of stratigraphy. However, this does not impinge on the key time period of study here.
Both Dob’s Linn and Anticosti are known for their well-studied Hirnantian stratigraphy, and both sections have been correlated to each other, in addition to other global Hirnantian sections (Jones et al., 2011; Melchin et al., 2013). These correlations are used in the main text.

Figure S-1 Sample location maps. (a) Palaeogeographic location map, with sample locations highlighted (adapted from Finlay et al., 2010); (b) Current geography of sample locations from Scotland and Anticosti Island; (c) Detail of sample locations on Anticosti Island; (d) Detail of sample location of Dob’s Linn.
Methods Description
Carbonate leaching
The leaching methods used for Li isotopes for bulk carbonates are described in Pogge von Strandmann et al. (2013). Briefly, samples were leached for 1 hour at room temperature in 0.1 M HCl. The possibility of leaching interstitial silicates was assessed by monitoring elemental ratios such as Al/Ca and Mn/Ca. Leaching experiments show that Al/Ca must be greater than >0.8 mmol/mol before silicate-derived Li will perturb the δ7Li measured in carbonates (Pogge von Strandmann et al., 2013). Al/Ca in our samples were below 0.6 mmol/mol (average 0.3 mmol/mol).
Fossil leaching
Large fossils were cut out of the rock using a diamond-tipped saw. The same technique was used to cut the centre of the fossil into an approximate cube a few mm on each side. This cube was then leached, using the sequential extraction method trialled by Pogge von Strandmann et al. (2013): 5 hours at room temperature in Na acetate buffered to pH 5 by acetic acid (Tessier et al., 1979; Pogge von Strandmann et al., 2013). These conditions were used to ensure no attack of any potential silicate material, and to contrast leaching methods with those used for bulk carbonates.
Shale leaching
In theory, authigenic silicates formed in seawater should take up their cations from seawater, meaning that authigenic clay δ7Li should represent seawater δ7Li, once clay-caused fractionation has been accounted for (Hathorne and James, 2006; Misra and Froelich, 2012; Pogge von Strandmann et al., 2013; Lechler et al., 2015). Marine shales could contain Li in several different fractions: exchangeable (i.e. sorbed), carbonates, authigenic silicates and potentially detrital silicates. To account for this, three of the Dob’s Linn shales were sequentially extracted (Tessier et al., 1979) for the exchangeable (1 hour in 1 M NaOAc), carbonate (5 hours in 1 M NaOAc buffered to pH 5 by acetic acid) and silicate fractions (residual silicates, dissolved by HF-HNO3, followed by HNO3 and HCl).
These values were compared to most of the shale samples, which were dissolved as bulk silicates, in the same manner as the residual silicates described above.
XRF and XRD analyses
Aliquots of cleaned Dob’s Linn samples utilised for Re-Os analysis were analysed by XRD at the University of St. Andrews and XRF at Origin Analytical Ltd. X-ray diffraction (XRD) samples were analysed by Mr Angus Calder at the University of St Andrews. Samples were crushed to a <5 μm powder using an agate ball mill in acetone and dried at 38 °C overnight. The powder was then back-packed into standard Philips sample holders to produce maximum random orientation. Analysis was then undertaken using a Philips PW1050/Hiltonbrooks DG2 X-ray diffractometer providing typical detection limits of 1–3 %. Quantification of mineral abundances was undertaken using a Reitveld method and SiroQuant v.3 software (http://www.siroquant.com/). The X-ray fluorescence (XRF) samples were analysed using Origin Analytical in house protocols (https://originanalytical.com/process/xrf/). Briefly, samples were powdered using an agate ball mill and then compacted to form a pellet. These were then analysed on a Spectro Xepos energy dispersive XRF. Raw data was corrected using in house and commercial standards that were analysed alongside the Dob’s Linn samples.
Results
Table S-1 Li isotope and trace element data from the section studies here.
| Height | δ7Li | 2 sd | Li/Ca | Mg/Ca | Al/Ca | Mn/Ca | Sr/Ca | |
| m | µmol/mol | mmol/mol | mmol/mol | mmol/mol | mmol/mol | |||
| Point Laframboise | ||||||||
| L-M-54 | 180.8 | 10.8 | 0.1 | 11.1 | 34.6 | 0.2 | 2.1 | 2.3 |
| L-M-56 | 184.4 | 8.0 | 0.7 | 17.5 | 46.5 | 0.5 | 2.7 | 1.0 |
| L-M-58 | 188 | 10.1 | 0.2 | 18.5 | 43.2 | 0.4 | 2.7 | 2.8 |
| L-M-60 | 189.8 | 11.8 | 0.7 | 46.3 | 61.6 | 0.2 | 3.6 | 1.2 |
| L-M-61 | 190.7 | 11.9 | 0.4 | 30.5 | 41.6 | 0.6 | 3.4 | 1.2 |
| L-M-64 | 193.3 | 14.2 | 0.1 | 11.8 | 27.8 | 0.2 | 2.3 | 0.9 |
| L-M-66 | 195.1 | 13.8 | 0.1 | 12.4 | 26.3 | 0.3 | 5.3 | 1.2 |
| L-M-67 | 196 | 18.7 | 0.5 | 33.6 | 413.7 | 0.6 | 8.9 | 1.2 |
| PL-5i | 198 | 17.6 | 0.7 | 23.2 | 297.8 | 0.4 | 8.5 | 1.3 |
| L-M-69 | 199 | 15.6 | 0.1 | 13.1 | 96.9 | 0.2 | 3.1 | 1.0 |
| PL-8i | 200 | 14.9 | 0.7 | 10.2 | 376.3 | 0.2 | 7.4 | 1.1 |
| PL-13i | 201.8 | 12.4 | 0.1 | 17.9 | 47.5 | 0.3 | 2.3 | 1.4 |
| PL-17Bi | 203.8 | 8.4 | 0.2 | 12.1 | 31.8 | 0.2 | 3.5 | 0.7 |
| PL-18i | 204.1 | 10.2 | 0.6 | 5.0 | 63.4 | 0.1 | 3.0 | 1.1 |
| PL-19Ai | 204.3 | 11.4 | 0.2 | 20.7 | 15.6 | 0.2 | 1.2 | 0.6 |
| PL-22i | 205.3 | 8.7 | 0.1 | 9.0 | 30.1 | 0.1 | 3.7 | 0.9 |
| PL-27i | 207.5 | 13.0 | 0.3 | 11.7 | 24.7 | 0.3 | 1.8 | 1.2 |
| Large fossils | ||||||||
| 194.5 | 12.1 | 1.1 | 10.2 | 31.2 | 0.1 | 2.1 | 1.2 | |
| 198 | 18.2 | 0.4 | 20.5 | 42.8 | 0.2 | 2.6 | 1.4 | |
| 198 | 17.6 | 0.6 | 23.2 | 24.3 | 0.2 | 3.1 | 1.3 | |
| 200 | 16.1 | 0.4 | 20.7 | 28.9 | 0.1 | 4.4 | 1.0 | |
| 200 | 16.2 | 0.3 | 21.4 | 41.6 | 0.1 | 3.4 | 0.9 | |
| 200.4 | 14.2 | 0.3 | 15.1 | 38.0 | 0.1 | 2.9 | 1.0 | |
| Ellis Bay West | ||||||||
| E-M-1 | 0 | 11.2 | 0.6 | 44.0 | 88.2 | 0.2 | 4.2 | 1.3 |
| E-M-3 | 1 | 8.8 | 0.9 | 25.0 | 54.6 | 0.5 | 3.5 | 1.0 |
| E-M-4 | 1.5 | 11.2 | 0.6 | 20.6 | 82.9 | 0.1 | 0.8 | 1.2 |
| E-M-7 | 3 | 10.4 | 0.1 | 33.1 | 113.1 | 0.4 | 0.9 | 1.6 |
| E-M-9 | 4 | 10.8 | 0.6 | 20.9 | 63.4 | 0.0 | 0.7 | 1.0 |
| E-M-11 | 5 | 12.3 | 0.6 | 14.7 | 43.6 | 0.0 | 0.6 | 0.8 |
| E-M-16 | 7.5 | 18.5 | 0.7 | 26.1 | 237.2 | 0.4 | 1.2 | 1.3 |
| E-M-18 | 8.5 | 19.6 | 1.0 | 13.5 | 318.1 | 0.2 | 6.7 | 1.0 |
| E-M-19 | 9 | 14.8 | 0.6 | 11.7 | 57.6 | 0.1 | 3.0 | 1.3 |
| E-M-21 | 9.8 | 13.5 | 0.7 | 5.0 | 12.3 | 0.4 | 0.3 | 0.7 |
| E-M-25 | 11 | 14.3 | 0.2 | 38.0 | 155.6 | 0.3 | 3.7 | 1.1 |
| E-M-31 | 12.8 | 10.2 | 0.5 | 8.5 | 23.5 | 0.5 | 0.7 | 1.0 |
| E-M-35 | 16.5 | 15.7 | 0.4 | 10.4 | 26.3 | 0.0 | 1.1 | 1.2 |
| E-M-39 | 20.5 | 11.8 | 0.8 | 9.5 | 29.2 | 0.4 | 0.2 | 1.2 |
| E-M-46 | 27.5 | 15.2 | 1.0 | 11.3 | 26.4 | 0.3 | 0.2 | 1.3 |
| Dob's Linn | ||||||||
| AF20-07 | 0.9 | -0.7 | 1.1 | |||||
| DS2-04 | -0.03 | -0.2 | 0.9 | |||||
| AF07-07 | -1.1 | -3.1 | 0.8 | |||||
| AF32-07 | -1.6 | -1.0 | 0.4 | |||||
| AF23-07 | -1.7 | 2.0 | 0.7 | |||||
| AF24-07 | -2.2 | 2.3 | 0.3 | |||||
| AF26-07 | -2.7 | 5.6 | 0.3 | |||||
| AF27-07 | -3.1 | 5.3 | 0.4 | |||||
| AF11-07 | -3.69 | 5.3 | 0.9 | |||||
| AF12-07 | -4.38 | 0.2 | 0.2 | |||||
| AF29-07 | -5 | 0.6 | 0.3 | |||||
| AF15-07 | -5.88 | -3.6 | 1.3 | |||||
| AF30-07 | -5.9 | -1.6 | 0.4 | |||||
| AF31-07 | -7.1 | -1.3 | 1.4 | |||||
Shale as a Li archive
Shales can comprise two types of silicate material: marine authigenic clays and detrital clays. Marine authigenic clays are one of the primary Li sinks from seawater. As such, they should incorporate Li from seawater, with a fractionation factor to δ7Li (∆7Liwater-clay ~15 ‰) during precipitation (Chan et al., 1992, 1994, 2002; Hathorne and James, 2006; Misra and Froelich, 2012; Pogge von Strandmann et al., 2013), and therefore should be an archive of seawater δ7Li. In contrast, detrital clays (i.e. those washed off the continents) will have formed from river water or soil pore waters, which in the modern environment tend to have a δ7Li value lower than seawater. Theoretically, detrital clays (which have a similar fractionation factor to authigenic clays) will have a δ7Li lower than that of authigenic clays because rivers generally have a lower δ7Li than seawater, although the precise difference will depend on clay mineralogy, degree of water-rock interaction and degree of incorporation vs. adsorption of Li. A study of detrital material through Earth history has suggested that their δ7Li values tend to reflect pre-depositional continental weathering processes (Li et al., 2016).
The shales from Dob’s Linn are dominated by detrital materials, and therefore its δ7Li values are likely to reflect continental weathering processes. Hence, the δ7Li change in the section reported in this study may either reflect changing weathering conditions (i.e. changing weathering congruency) or a change in clay mineralogy – where both possibilities are reflections of changing weathering processes. Recent studies have examined the Li isotope behaviour in modern riverine suspended material, and found that source rock variability and suspended load grain size, as well as chemical weathering processes, can affect the δ7Li of silicate particles (Dellinger et al., 2014, 2017). In order to assess any possible effect of provenance, we compare the shale δ7Li to the provenance tracers Os isotopes (187Os/188Os) and Li/Al ratios (Table S-2). Neither correlates with Li isotopes, strongly suggesting that provenance is not controlling the δ7Li of these shales (Fig. S-2). We also note that suspended sediments in the Ganges show no provenance effect (Pogge von Strandmann et al., 2017). In order to assess any grain size effect, we compare shale δ7Li and [Li] to the standard Si/Al tracer, and also find no correlation (Fig. S-2). We note that in the global modern riverine sediment compilation of Dellinger et al. (2017), the Li concentrations of our shales plot towards the low [Li] highly weathered lowland end-member, which would be expected, given the detrital origin of the shales.

Figure S-2 Lack of correlation between δ7Li and grain size tracer Si/Al, and provenance tracers Li/Al and Os (Osi = 187Os/188Os) isotopes.
The possibility of changing clay mineralogy causing a change in fractionation factor in the shales was assessed by comparing δ7Li to mineralogical analyses (Table S-3). While clays such as illite vary within the shale section, their abundance does not correlate with δ7Li, suggesting that changing mineralogy is not controlling Li isotope ratios (Fig. S-3).

Figure S-3 Lack of significant correlation between shale δ7Li and secondary mineralogy.
If the shale δ7Li does reflect river or soil pore water δ7Li, then the positive excursion in the shales would reflect a positive excursion in the solutions. This is because standard isotope behaviour (whether equilibrium or kinetic) requires that for a constant fractionation factor α (constant clay mineralogy), the isotope ratio of two linked phases will behave in parallel. Figure S-4 shows an example of this behaviour, for a constant α = 0.99 and an initial rock composition of 5 ‰. Regardless of the fractionation mechanism (solid lines = equilibrium, dotted lines = Rayleigh), the δ7Li of the corresponding solutions and clays (or shales) behave in parallel for a given weathering congruency (f = fraction of Li in solution relative to that taken up by clays). Overall this shows that a change in weathering congruency would drive rivers and clays that precipitate from those rivers in the same isotopic direction.

Figure S-4 Example of isotope fractionation behaviour of two linked phases (in this case water and clay) for a constant fractionation factor. Solid lines represent equilibrium fractionation, while dotted lines represent Rayleigh fractionation.
It is also possible that the detrital clays reacted with Hirnantian seawater once they left the continents. Evidence from basaltic particles in estuaries (the only study performed to date) show that these particles continue to weather (Jones et al., 2014), forming clay minerals (i.e. authigenic ones) and fractionating Li isotopes (Pogge von Strandmann et al., 2008). In this case, the δ7Li composition of the shales would be a more direct reflection of seawater δ7Li. We stress that shale or clay records are not well-constrained enough to use in isolation as yet, but that the comparison between shales and carbonates yields some insight into processes, or at least that the observed δ7Li excursions may not be entirely local.
If chemostratigraphy (i.e. the assumption that the C isotope excursions are synchronous) is used to establish the relative timing between Anticosti and Dob’s Linn, then the Li excursions are approximately synchronous, which would be expected given the long modern residence time of Li (~1 Myr). However, biostratigraphy of the graptolite zone N. persculptus suggests that the C isotope excursions of the locations are not entirely synchronous (Melchin et al., 2013) (Fig. 1, main text). Hence, hiatuses or changes in rates of deposition may have altered the comparison of the sedimentary records, different parts of the Iapetus Ocean may have different relative timings of graptolite occurrence or C isotope excursion (Melchin et al., 2003), or local watermass chemistry variations owing to circulation or sea-level changes may have existed (Holmden et al., 2012).
Table S-2 XRF major element concentration data (in wt. %) for the shales.
| Al2O3 | SiO2 | TiO2 | Fe2O3 | MnO | MgO | CaO | Na2O | K2O | P2O5 | |
| AF-32-07 | 19.44 | 66.01 | 0.78 | 7.27 | 0.71 | 3.37 | 0.22 | 0.78 | 3.30 | 0.14 |
| AF-27-07 | 10.84 | 43.13 | 0.53 | 6.02 | 1.07 | 6.07 | 8.16 | 0.35 | 2.04 | 0.08 |
| AF-12-07 | 14.87 | 56.44 | 0.85 | 2.78 | 0.01 | 1.38 | 0.29 | 0.28 | 4.14 | 0.03 |
| AF-07-07 | 14.52 | 54.85 | 0.80 | 6.16 | 0.11 | 2.63 | 0.22 | 0.41 | 3.03 | 0.11 |
| DS2-04 | 17.12 | 60.33 | 0.66 | 8.46 | 0.02 | 3.25 | 0.00 | 2.77 | 3.03 | 0.05 |
| AF-30-07 | 13.76 | 50.98 | 0.68 | 6.56 | 0.04 | 2.69 | 0.19 | 0.66 | 2.86 | 0.06 |
| AF-04-07 | 14.47 | 53.62 | 0.67 | 4.91 | 0.02 | 2.34 | 0.10 | 1.01 | 3.17 | 0.04 |
| AF-24-07 | 13.74 | 50.38 | 0.67 | 4.91 | 0.54 | 4.57 | 5.38 | 0.34 | 2.85 | 0.16 |
| AF-31-07 | 19.79 | 61.79 | 0.84 | 7.95 | 0.10 | 3.93 | 0.31 | 0.81 | 3.53 | 0.06 |
| AF-11-07 | 15.27 | 53.75 | 0.78 | 2.70 | 0.02 | 1.51 | 0.34 | 0.30 | 3.97 | 0.04 |
| AF-26-07 | 12.30 | 46.45 | 0.63 | 5.01 | 0.56 | 4.21 | 5.18 | 0.25 | 2.60 | 0.10 |
| AF-29-07 | 19.13 | 67.47 | 0.76 | 6.13 | 0.04 | 3.62 | 0.25 | 0.97 | 3.39 | 0.07 |
Table S-3 Quantitative mineralogy data from some of the shale samples.
| Siroquant Quantitative Analysis | AF0406 | DS104 | AF0807 | AF23A07 | AF26A07 | AF27A07 |
| (wt. %) | ||||||
| Anhydrite | - | - | - | - | - | - |
| Ankerite | - | - | - | 6 | 17 | 30 |
| Calcite | - | - | - | 3 | 3 | 1 |
| Chlorite | - | 12 | 7 | 10 | 8 | 7 |
| Dolomite | 1 | - | - | - | - | - |
| Gypsum | - | - | - | - | - | - |
| Illite/Muscovite | 36 | 41 | 32 | 35 | 29 | 21 |
| Kaolinite | 9 | 3 | 2 | - | 3 | 2 |
| K-Feldspar | 3 | - | - | - | - | - |
| Plagioclase | 1 | 7 | 12 | 10 | 8 | 8 |
| Pyrite | 7 | 5 | 2 | - | - | 1 |
| Quartz | 43 | 32 | 45 | 36 | 32 | 30 |
To examine the potential of a shale archive in more detail, several of the shale samples were also sequentially leached (Tessier et al., 1979), to determine the proportion and isotope composition of Li in exchangeable sites, the carbonate fraction and residual silicates.
The residual silicates have identical δ7Li within analytical uncertainty to bulk shales. This is because >94 % of Li resides within the silicate fraction. Only ~2 % is in exchangeable sites, and ~4 % in carbonates. Exchangeable δ7Li is ubiquitously isotopically heavier than the bulk shales, and is generally similar to samples that have adsorbed Li from modern seawater, suggesting that the sorbed fraction represents more recent interaction with seawater, or seawater-derived aerosols via rain.
The carbonate fraction δ7Li is highly variable, and in some samples is similar to that of the silicate fraction, while in others is similar to the exchangeable fraction. This suggests that in these shales, the carbonate fraction has exchanged cations with other sources of Li, and therefore in silicate-rich rocks, carbonates are not a reliable archive for seawater Li.
In the case of these shales, the residual detrital silicates or bulk silicates appear to be a reliable Li archive of continental weathering processes (rather than necessarily an archive of seawater).
Table S-4 Results of sequential leaching of some of the Dob’s Linn shales.
| δ7Li | 2 sd | % of bulk Li | |
| AF23-07 | |||
| Exchangeable | 13.1 | 0.6 | 1.5 |
| Carbonate | 8.6 | 0.3 | 3.5 |
| Residue | 2.7 | 0.2 | 95 |
| Bulk | 2.0 | 0.7 | |
| AF11-07 | |||
| Exchangeable | 15.6 | 0.6 | 0.8 |
| Carbonate | 14.3 | 1.0 | 2.2 |
| Residue | 4.7 | 0.1 | 97 |
| Bulk | 5.3 | 0.9 | |
| AF15-07 | |||
| Exchangeable | 1.5 | 0.5 | 2 |
| Carbonate | -3.0 | 0.5 | 4 |
| Residue | -2.5 | 0.4 | 94 |
| Bulk | -3.6 | 1.3 | |
Potential lithology control in carbonates
To demonstrate that the carbonate δ7Li values from Anticosti are not affected or controlled by varying lithologies through the sections, Figure S-5 compares the stratigraphy of those sections to the isotope data. It is clear that the carbonate δ7Li values do not correspond to changing lithology or presence of shale.

Figure S-5 Anticosti section lithology (Desrochers et al., 2010; Achab et al., 2011, 2013; Copper et al., 2013), compared to isotope data.
Model Description
Table S-5 Definitions of parameters used in the models.
| Symbol | Parameter |
| A | Ocean-atmosphere reservoir of DIC/CO2 (mol) |
| A0 | Modern reservoir (mol) |
| Fd | Degassing flux of CO2 input (mol) |
| Fw | Silicate weathering flux of CO2 consumption (mol) |
| D | Normalised degassing parameter |
| U | Normalised uplift parameter |
| kV | Fraction of present weathering rate in the absence of plants |
| ∆T | Temperature change (K) |
| Lithium | |
| Fr | Riverine Li flux |
| Fh | Hydrothermal Li flux |
| Fsed | Removal of Li into ocean secondary sediments |
| R | Isotope ratio |
| N | Ocean reservoir of Li (mol) |
| kLi | Partition coefficient of oceanic Li sink |
| kh | Modern hydrothermal Li input (mol) |
| kw | Modern riverine Li input (mol) |
| ∆sink | Li isotopic fractionation factor imposed by the Li sink |
Coupled carbon cycle and Li isotope model
We formulated a simple model coupling the carbon and lithium cycles in order to examine hypotheses for the cause of Late Ordovician (Hirnantian) glaciation and associated Li isotope variations in a consistent way. The model uses the formulation of the time-varying oceanic Li reservoir and its isotopic composition from previous work (Pogge von Strandmann et al., 2013; Lechler et al., 2015), but instead of prescribing the weathering flux of Li we link it to the silicate weathering flux calculated by the carbon cycle model. We also couple the volcanic input of CO2 and the hydrothermal input of Li via a common degassing parameter, linked to seafloor spreading.
The baseline Ordovician δ7Liocean indicates an unfractionated (0–3 ‰) weathering flux. Given that the composition of the modern upper continental crust (δ7Li ~0 ‰; Sauzeat et al., 2015) is only isotopically lighter than the mantle (~3 ‰; Pogge von Strandmann et al., 2011) due to clay formation during weathering, if such fractionation were not occurring prior to the Hirnantian, unfractionated silicate rocks would have a mantle-like composition. If congruent weathering (minimal clay formation) were occurring, it is reasonable to associate the weathering flux of Li directly with the silicate weathering flux of cations and associated alkalinity. However, once there is substantial incorporation of Li into clays (with associated δ7Li fractionation) this assumption can break down.
Simple carbon cycle and weathering model
We base our simple carbon cycle model on GEOCARB III and strive for an analytical formulation in the interests of clarity. One point of difference from GEOCARB is that we assume the proportion of ocean-atmosphere carbon (A) that resides in the atmosphere scales with A2, so that CO2 (normalised to PAL i.e. multiples of present atmospheric level) is:
Eq. S-1
CO2 = (A/A0)2
where A0 = 3.2 × 1018 mol C (the present atmosphere-ocean carbon reservoir) (Kump and Arthur, 1999). This does not affect the steady state predictions of CO2 but it means that higher Palaeozoic steady state CO2 values correspond to smaller increases in the steady state ocean-atmosphere carbon reservoir. Therefore in transient simulations the total reservoir responds more rapidly.
Global temperature (expressed as deviation from the present temperature, ∆T) depends on solar luminosity (which was ~4.5 % lower in the Ordovician) and on CO2, following the simple relationship from GEOCARB:
Eq. S-2
ΔΤ = kc * ln(CO2) − kl * (τ/570)
where kc = 4 °C (corresponding to a relatively low climate sensitivity of about 2.8 °C for doubling CO2) and kl = 7.4 °C for t in Myr ago, which gives ~5.8 °C cooling at 450–445 Ma due to lower solar luminosity. Hence we use:
Eq. S-3
ΔΤ = kc * ln(CO2) − 5.8
The silicate weathering flux depends on several factors, including atmospheric CO2, temperature, T, vegetation, V (or lack thereof), and uplift, U (normalised).
Eq. S-4
Fw = kw * U * ƒ(V) * ƒ(CO2) * ƒ(Τ)
Initially we assume an abiotic weathering regime (as early plants were just starting to colonise the land in the mid–late Ordovician). This can be parameterised as f(V) = kv, which represents the reduction in weathering rate in the absence of plants. Following GEOCARB III we assume kv = 0.25 (i.e. a ~4 fold reduction in weathering rate). We take the dependence of weathering rate on CO2 under abiotic conditions from GEOCARB:
Eq. S-5
ƒ(CO2) = (CO2)0.5 = A/A0
For the effect of temperature on weathering we neglect the indirect effects of changes in runoff (because these are relatively small in the GEOCARB formulation) and consider just the kinetic effect of temperature on mineral dissolution, which using an activation energy appropriate for granite is:
Eq. S-6
ƒ(Τ) = e(0.09 * ΔΤ)
Substituting Eqs. S-5 and S-6, this reduces to:
Eq. S-7
ƒ(Τ) = (CO2)0.36/1.685 = (A/A0)0.72/1.685
Then combining Eqs. S-4 and S-7, we have:
Eq. S-8
Fw = kw * U * kv * (A/A0)1.72/1.685
As silicate weathering is a sink for carbon this represents a negative feedback on variations in ocean-atmosphere carbon, A. The overall carbon balance can be written in its simplest form as:
Eq. S-9
dA/dt = Fd − Fw
where Fd = carbonate carbon degassing flux of CO2 input and Fw = silicate weathering (and subsequent carbonate burial) flux of CO2 consumption. This follows GEOCARB III in assuming that oceanic carbonate is in steady state, hence carbonate weathering is balanced by a corresponding flux of carbonate burial. It also assumes that the organic carbon cycle is in balance.
Carbonate degassing can be treated as a normalised parameter, D, linked to sea floor spreading rate (and therefore hydrothermal activity):
Eq. S-10
Fd = kw * D
Inserting Eqs. S-8 and S-10 into Eq. S-9:
Eq. S-11
dA/dt = kw*D − kw*U*kv*(A/A0)1.72/1.685
Assuming steady state (dA/dt = 0, Fw = Fd) and rearranging gives:
Eq. S-12
A/A0 = (D*1.685/U*kv)1/1.72 = (D*1.685/U*k v)0.58
For the Late Ordovician background conditions we follow GEOCARB III and assume elevated degassing, D = 1.55, relatively high uplift as at present, U = 1, and kV = 0.25. This gives A/A0 = 3.9, CO2 = 15.2 PAL, and ∆T = +5.1 °C (i.e. global average T ~ 20 °C), with CO2 and ∆T comparing well with GEOCARB III for the Ordovician (Berner and Kothavala, 2001), indicating that the simplified overall carbon balance is reasonable.
For a present day silicate weathering (and carbonate degassing) flux of kw ~ 7 × 1012 mol C/yr and the modern reservoir A0 = 3.2 × 1018 mol C this gives a carbon residence time of ~450 kyr with respect to removal by silicate weathering. For the Ordovician conditions above, the carbon residence time increases to ~1.15 Myr.
Lithium cycle model
The behaviour of Li and its isotopes through time was modelled using the dynamic (non-steady state) box models used in Pogge von Strandmann et al. (2013) and Lechler et al. (2015). The models were constructed from the standard dynamic mass balance equation used for all isotope systems, and shown here for Li:
Eq. S-13
dN/dt = Fr + Fh − Fsed
where N is the seawater Li reservoir, and Fx represents the input and output fluxes (r = river, h = hydrothermal, sed = sediment (combined alteration of the oceanic crust, and uptake onto marine sediments)). The isotopic balance equation is then given by:
Eq. S-14
N dRSW/dt = Fr(Rr − RSW) + Fh(Rh − RSW) − Fsed(Rsed − RSW)
where Rx is the isotope ratio of the various fluxes. Rsink is given by ∆sink = Rsink-RSW, where ∆7Lisink = 15–16 ‰ (Chan et al., 1993; Huh et al., 1998; Misra and Froelich, 2012). Finally, the calculation of the sink of Li (and all other elements modelled here) from seawater is based on the assumption that partitioning into the sink is due to a constant partition coefficient kLi, where:
Eq. S-15
Fsed = kLi*N
This model clearly shows that the hydrothermal input in isolation (Fh) is not a significant driver of the δ7Li composition of seawater. For example, a 50 % decrease in the global hydrothermal flux (significantly greater than postulated for the Phanerozoic), would result in an increase of seawater δ7Li by only 0.6 ‰. We also refer the reader to the Supplement of Pogge von Strandmann et al., (2013).
Coupled Li and carbon cycle model
In this study the lithium cycle is coupled to the carbon cycle in two ways:
(1) The hydrothermal input flux of lithium, Fh, is taken to scale with sea floor spreading rate and therefore degassing (i.e. it starts at D = 1.55 times the modern value):
Eq. S-16
Fh = kh * D
where kh = 6 × 109 mol Li/yr, so with D =1.55, Fh = 9.3 × 109 mol Li/yr.
(2) The riverine flux of lithium, Fr, is assumed proportional to the silicate weathering flux:
Eq. S-17
Fr = kr * Fw/kw
The riverine lithium flux is also adjusted upwards to account for the lack of a clay formation sink for lithium such that Fr is assumed to be initially twice the modern value. At steady state Fw/kw = D = 1.55, so kr = 1.29 × 1010 mol Li/yr gives Fr = 2 × 1010 mol Li/yr.
Solving the lithium model for steady state:
Eq. S-18
N = (Fr + Fh)/kLi
where kLi = 10-6 yr-1. Hence N = 2.93 × 1016 mol Li in the initial steady state and the (prescribed) residence time of 1 Myr is comparable to that of carbon.
Solving the lithium isotope equation at steady state gives:
Eq. S-19
Rsed = Rr*Fr/(Fr + Fh) + Rh*Fh/(Fr + Fh) and Rsw = Rsed + Δsink
which for Rr = 3, Rh = 7, ∆sink = 15 gives Rsed = 4.27, and Rsw = 19.2 or for Rr = 0 (with Rh = 7, ∆sink = 15) gives Rsed = 2.2, and Rsw = 17.1.
To consider transient scenarios, the combined carbon-lithium model is solved numerically.
Scenarios for initiating/triggering glaciation
Existing climate model studies (e.g., Pohl et al., 2016) indicate that CO2 needs to halve to ~8 PAL to trigger glaciation in the Late Ordovician (even though this is still ∆T = +2.5 °C relative to today according to the simple formula). This corresponds to a drop to A/A0 = 2.8 (from A/A0 = 3.9). Such a drop in ocean carbon and atmospheric CO2 could be achieved through a decline in degassing (D), an increase in uplift (U), the onset of vegetation (increasing kv), or some other factor increasing weatherability.
(i) Declining degassing
Recently it has been proposed (McKenzie et al., 2016) that there was a Late Ordovician decrease in continental volcanic arc degassing (possibly linked to the cessation of Appalachian volcanic arc formation). If there was a large reduction in global degassing it could have triggered glaciation, e.g., a drop from D = 1.55 to D = 0.75 creates a drop in A/A0 to ~2.5 and CO2 to ~6.5 PAL. This is an extreme scenario given that the bottom end of the Phanerozoic range in degassing is usually taken to be D ~ 0.9.
The corresponding changes in the Li system are Fr = 9.7 × 109 mol Li/yr, Fh = 4.5 × 109 mol Li/yr, N = 1.42 × 1016 mol Li. As both the riverine and hydrothermal fluxes of lithium scale proportionally to degassing then at steady state there is no change to the lithium isotope composition of the ocean and the sedimentary flux. However, during the transient adjustment of the Li reservoir, the sink of Li must exceed the inputs and as the sink is very isotopically depleted relative to the reservoir it is draining (by ∆sink = 15) then the ocean becomes transiently enriched in δ7Li. As long as the forcing (decline in degassing) is relatively rapid e.g., occurs in the order of ~1 Myr, the positive δ7Li excursion is ~3.5 ‰ (it becomes somewhat smaller for a slower decline in degassing).

Figure S-6 Result of a permanent decrease in degassing on the Li isotope composition of the oceans. Note that this scenario assumes Rr = 3 ‰.
This is not enough to explain the full δ7Li change seen in the data, but it is a substantial signal. Hence a fairly abrupt and large decline in degassing can explain planetary cooling coincident with a positive δ7Li excursion, with no change in fractionation factors (i.e. assuming congruent weathering throughout).
ii) Land colonisation by vegetation accelerating weathering
Previous work (Lenton et al., 2012; Lenton et al., 2016) has explored a ~65 % global increase in weathering rate with the first non-vascular land plants. This could be likened to increasing kv from 0.25 to 0.41 (although in the full COPSE model the functional dependence of weathering on CO2 also starts to change). This gives A/A0 = 2.9 and CO2 = 8.6 PAL, close to the predicted threshold for glaciation. As degassing has not changed, the steady state weathering and hydrothermal fluxes are unchanged, and therefore there is no change in the steady state Li reservoir or its isotopic composition. If kv is increased relatively rapidly e.g., in 1 Myr, then a transient excess of weathering creates a modest transient rise in ocean Li and a small transient dip in ocean δ7Li. However, if one does the same forcing more slowly, the transient changes in ocean Li and δ7Li are damped down. Thus a slower plant colonisation sufficient to trigger glaciation would not show up in δ7Li via its effects on Li fluxes.

Figure S-7 Result of a permanent increase in vegetation cover on the Li isotope composition of the oceans. Note that this scenario assumes Rr = 3 ‰.
However, land colonisation by vegetation will show up in δ7Li if early plants started making soils and clays (as would be expected), through initiating incongruent weathering, which drives riverine δ7Li more positive (as isotopically depleted Li is preferentially stored in the clays). Increasing δ7Li river from 3 to 13 ‰ concomitant with increasing kv from 0.25 to 0.41 creates a (permanent) shift in δ7Li ocean to 26 ‰ in tandem with the cooling.

Figure S-8 Result of a permanent increase in vegetation cover combined with an increase in riverine δ7Li on the Li isotope composition of the oceans.
To explain why oceanic δ7Li returns to its original value one must therefore argue that glaciation caused a return to more congruent weathering, i.e. δ7Liriver = 3 ‰. This might be argued on the grounds that glaciation suppressed early vegetation, or that it scoured off newly formed soils in some regions. If we simply reduce kv from 0.41 to 0.25 over 2–3 Myr in the model run, and with it reduce δ7Liriver from 13 to 3 ‰, then δ7Li is brought back to its initial pre-excursion value (Fig. S-9).

Figure S-9 Identical scenario to Figure S-8 (increase in vegetation cover combined with an increase in riverine δ7Li), but combined with a subsequent decrease in kv and Rr.
iii) Alternative change in weathering congruency
It is mathematically possible that the observed positive δ7Li excursion in marine carbonates was caused by a change in the silicate weathering congruency (increase in riverine δ7Li), with no concomitant change in the riverine flux. A transient 15 ‰ increase in Rr (3–18 ‰) would temporarily drive seawater δ7Li to ~24 ‰ (Fig. S-10). However, this scenario has no direct forcing of the carbon cycle and therefore no change in CO2 or glaciation is created in the model. In addition, the Hirnantian represents a switch to generally drier and colder conditions, which both tend to cause less, rather than more, clay formation.
We also note that generating a change in riverine δ7Li with no change in Li flux is unlikely, because the relatively greater formation of secondary minerals would decrease the Li flux together with increasing river δ7Li (Pogge von Strandmann et al., 2006; Pogge von Strandmann et al., 2013; Dellinger et al., 2015; Wanner et al., 2017). Alternatively, such a change could be caused by a change in the secondary mineral fractionation factor, for example by a change in secondary mineralogy. However, such a large shift (15 ‰) is considerably greater than that observed in modern natural samples (Huh et al., 1998; Dellinger et al., 2015; Pogge von Strandmann et al., 2017), and would also have to occur on a global scale. Modern river weathering studies have also proposed that changes in secondary mineralogy are minor effects on riverine δ7Li (Liu et al., 2015). Finally, the Dob’s Linn shales show no correlation between clay mineral abundance and δ7Li.
This is why we favour an approach that generates a plausible change in the carbon cycle and climate (and hence also the Li flux) and then considers if an additional fractionation effect needs to be invoked to explain the δ7Li data.

Figure S-10 A scenario where the seawater δ7Li excursion is solely caused by a change in river δ7Li (Rr) (but there is no associated change in the modelled carbon cycle and global temperature).
iv) Other forcing scenarios?
To achieve the same effect from an increase in uplift would require a 65 % increase in uplift above present values, which would be unprecedented for the Phanerozoic. As uplift is already assumed high in the Ordovician we do not consider this plausible.
Alternatively the creation of large areas of fresh basalt linked to e.g., continental volcanic arc creation will increase weatherability. However to increase global weatherability by the required ~65 % would need a very large area of basalts. Today basalts contribute around 35 % to the global weathering flux (Dessert et al., 2003) so one would need to go e.g., from zero basalt to roughly twice the present area of basalt. We do not consider this plausible, because there is no evidence of any Large Igneous Province of anywhere near sufficient size, although a hypothesised LIP has been modelled (Lefebvre et al., 2010). In addition, seawater δ7Li has been shown to be driven lower during basaltic eruptions at Oceanic Anoxic Events (Pogge von Strandmann et al., 2013; Lechler et al., 2015).
Scenarios once glaciation is triggered
We have two scenarios for triggering glaciation – a large decline in degassing or the onset of vegetation accelerating weathering – which could have acted in combination. Reducing degassing produces a transient peak in δ7Li coincident with cooling but the peak is not as large as in the data. Accelerating weathering does not affect δ7Li, but the onset of incongruent weathering (clay and soil formation) due to vegetation causes a permanent increase in δ7Li, whereas the data shows a drop in δ7Li as glaciation wanes. Hence we considered augmenting the two scenarios to try to better reproduce the data.
i) Abrupt glaciation and cooling
An important insight from recent work (Pohl et al., 2016) is that there could have been a glaciation ‘tipping point’ in the Late Ordovician, in which, once global temperature dropped to a critical threshold, sea-ice on the Northern Hemisphere ocean expanded abruptly to a new steady state coverage and with that global temperatures fell abruptly and an ice sheet grew on the Southern polar land surfaces. The responsible ice albedo and heat transport feedbacks operate far faster than the long-term carbon cycle timescales considered here. Hence to represent this we implement an abrupt cooling of kabrupt once ∆T < 2.5 °K (corresponding to CO2 ~ 8 PAL). Note that this represents an adjustment to the temperature calculation from Eq. S-3, which in turn means the steady state solutions to the equations given above are no longer valid (here we are solving the model numerically). To prevent an immediate abrupt warming as CO2 builds up in response we assume some bi-stability of temperature such that CO2 has to rise to ~12 PAL before an equivalent warming by kabrupt occurs. Overall this serves as a way for abrupt glaciation/cooling to reduce the silicate weathering flux in a manner consistent with the kinetics assumed for silicate weathering. If we assume kabrupt = -10 °C based on the results of Pohl et al. (2016), then this more than halves the weathering global weathering flux, causing an accelerated rise in δ7Li from 20 to ~23 ‰, which is reversed when build-up of CO2 triggers abrupt warming (i.e. peak δ7Li is predicted to be at the end of the glacial interval). The system will then oscillate unless one imposes some reversal of the forcing that triggered glaciation in the first place.

Figure S-11 Effect of an oscillatory system from the feedbacks described in the text on the relative temperature and seawater δ7Li values.
Although glacial-interglacial cycles have recently been suggested for the Late Ordovician (Ghienne et al., 2014), given that these are not resolved in our coarser stratigraphy, we opt to increase to D = 1.0 from 3–4 Myr into the model run to just produce one glaciation.

Figure S-12 Effect of single glaciation on the relative temperature and seawater δ7Li values.
Sensitivity analysis for temperature sensitivity of sink fractionation
We additionally considered a temperature sensitivity of ∆sink based on the studies summarised in Figure 3 of Li and West (2014). From their best-fit line we deduce that near the present surface temperature of the Earth (~288 °K) there is a sensitivity of ∆sink of -0.15 ‰/°K. In other words climate cooling leads to somewhat stronger fractionation. When we include this effect in the Figure S-12 scenario it slightly amplifies the peak δ7Li from 24.7 ‰ to 25.9 ‰, i.e. by 1.2 ‰ (Fig. S-13).

Figure S-13 The same scenario as in Figure S-12, but with an added temperature control on the fractionation factor of the Li sink.
Combined effects
A combination of all effects discussed above (change in weathering flux, temperature-dependence of the Li sink and a change in weathering congruency) is also possible. If the Dob’s Linn shale represents an archive into a local continental weathering record, it would imply that weathering congruency decreased during the glaciation, increasing river δ7Li (and hence increasing the δ7Li of clays precipitating from that water). Using the relative timing of the shale and carbonate records for the change in riverine δ7Li yields an excursion peak of ~25 ‰ (for a 0 ‰ starting composition) to ~27.2 ‰ (for a 3 ‰ starting composition) (Fig. S-14).

Figure S-14 The same scenario as in Figure S-13, except that riverine δ7Li also increases.
Sr isotope record
The seawater 87Sr/86Sr record was modelled using the standard dynamic mass balance equations provided in Pogge von Strandmann et al. (2013). The factors of change in the riverine and hydrothermal input fluxes from the Li model (e.g., Fig. S-12) were imposed into the Sr model (Fig. S-15). Using the suggested riverine isotope ratios from Young et al. (2009), the resulting seawater 87Sr/86Sr shows variability between ~0.7078 and 0.7080. Data from the Hirnantian shows scatter between 0.7078 and 0.7081 (Shields et al., 2003; Young et al., 2009). Hence, the variations determined from the coupled Li-C model do not cause Sr isotope variation beyond the scatter observed in the data, lending further credence to our interpretation.

Figure S-15 Modelled Sr isotope ratio of seawater, using factors taken from the Li-C model.
Supplementary Information References
Achab, A., Asselin, E., Desrochers, A., Riva, J.F. (2013) The end-Ordovician chitinozoan zones of Anticosti Island, Quebec: Definition and stratigraphic position. Review of Palaeobotany and Palynology 198, 92–109.
Armstrong, H.A., Owen, A.W. (2002a) Euconodont diversity changes in a cooling and closing Iapetus Ocean. In: Crame, J.A. and Owen, A.W. (Eds.) Palaeobiogeography and Biodiversity Change: The Ordovician and Mesozoic-Cenozoic Radiations. Geological Society, London, Special Publications 194, 85–98.
Armstrong, H.A., Owen, A.W. (2002b) Euconodont paleobiogeography and the closure of the Iapetus Ocean. Geology 30, 1091–1094.
Berner, R.A., Kothavala, Z. (2001) GEOCARB III: a revised model of atmospheric CO2 over phanerozoic time. American Journal of Science 301, 182–204.
Chan, L.H., Edmond, J.M., Thompson, G., Gillis, K. (1992) Lithium isotopic composition of submarine basalts: implications for the lithium cycle in the oceans. Earth and Planetary Science Letters 108, 151–160.
Chan, L.H., Edmond, J.M., Thompson, G. (1993) A lithium isotope study of hot springs and metabasalts from mid-ocean ridge hydrothermal systems. Journal of Geophysical Research 98, 9653–9659.
Chan, L.H., Gieskes, J.M., You, C.F., Edmond, J.M. (1994) Lithium isotope geochemistry of sediments and hydrothermal fluids of the Guaymas Basin, Gulk of California. Geochimica Et Cosmochimica Acta 58, 4443–4454.
Chan, L.H., Alt, J.C., Teagle, D.A.H. (2002) Lithium and lithium isotope profiles through the upper oceanic crust: a study of seawater-basalt exchange at ODP Sites 504B and 896A. Earth and Planetary Science Letters 201, 187–201.
Copper, P., Jin, J., Desrochers, A. (2013) The Ordovician-Silurian boundary (late Katian-Hirnantian) of western Anticosti Island: revised stratigraphy and benthic megafaunal correlations. Stratigraphy 10, 213–227.
Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Galy, V., Hilton, R.G., Louvat, P., France-Lanord, C. (2014) Lithium isotopes in large rivers reveal the cannibalistic nature of modern continental weathering and erosion. Earth and Planetary Science Letters 401, 359–372.
Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., Gorge, C., Alanoca, L., Maurice, L. (2015) Riverine Li isotope fractionation in the Amazon River basin controlled by the weathering regimes. Geochimica et Cosmochimica Acta 164, 71–93.
Dellinger, M., Bouchez, J., Gaillardet, J., Faure, L., Moureau, J. (2017) Tracing weathering regimes using the lithium isotope composition of detrital sediments. Geology 45, 411–414.
Desrochers, A., Farley, C., Achab, A., Asselin, E., Riva, J.F. (2010) A far-field record of the end Ordovician glaciation: The Ellis Bay Formation, Anticosti Island, Eastern Canada. Palaeogeography Palaeoclimatology Palaeoecology 296, 248–263.
Dessert, C., Dupre, B., Gaillardet, J., Francois, L.M., Allegre, C.J. (2003) Basalt weathering laws and the impact of basalt weathering on the global carbon cycle. Chemical Geology 202, 257–273.
Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
Hathorne, E.C., James, R.H. (2006) Temporal record of lithium in seawater: a tracer for silicate weathering? Earth and Planetary Science Letters 246, 393–406.
Holmden, C., Panchuk, K., Finney, S.C. (2012) Tightly coupled records of Ca and C isotope changes during the Hirnantian glaciation event in an epeiric sea setting. Geochimica et Cosmochimica Acta 98, 94–106.
Huh, Y., Chan, L.H., Zhang, L., Edmond, J.M. (1998) Lithium and its isotopes in major world rivers: Implications for weathering and the oceanic budget. Geochimica Et Cosmochimica Acta 62, 2039–2051.
Jones, D.S., Fike, D.A., Finnegan, S., Fischer, W.W., Schrag, D.P., McCay, D. (2011) Terminal Ordovician carbon isotope stratigraphy and glacioeustatic sea-level change across Anticosti Island (Québec, Canada). Geological Society of America Bulletin 123, 1645–1664.
Jones, M.T., Gislason, S.R., Burton, K.W., Pearce, C.R., Mavromatis, V., Pogge von Strandmann, P.A.E., Oelkers, E.H. (2014) Quantifying the impact of riverine particulate dissolution in seawater on ocean chemistry. Earth and Planetary Science Letters 395, 91–100.
Kump, L.R., Arthur, M.A. (1999) Interpreting carbon-isotope excursions: carbonates and organic matter. Chemical Geology 161, 181–198.
Lapworth, C. (1878) The Moffat series. The Quarterly journal of the Geological Society of London 34, 240–346.
Lechler, M., Pogge von Strandmann, P.A.E., Jenkyns, H.C., Prosser, G., Parente, M. (2015) Lithium-isotope evidence for enhanced silicate weathering during OAE 1a (Early Aptian Selli event). Earth and Planetary Science Letters 432, 210–222.
Lefebvre, V., Servais, T., Francois, L., Averbuch, O. (2010) Did a Katian large igneous province trigger the Late Ordovician glaciation?: A hypothesis tested with a carbon cycle model. Palaeogeography Palaeoclimatology Palaeoecology 296, 310–319.
Lenton, T.M., Crouch, M., Johson, M., Pires, N., Dolan, L. (2012) First plants cooled the Ordovician. Nature Geoscience 5, 86–89.
Lenton, T.M., Dahl, T.W., Daines, S.J., Mills, B.J., Ozaki, K., Saltzman, M.R., Porada, P. (2016) Earliest land plants created modern levels of atmospheric oxygen. Proceedings of the National Academy of Sciences 113, 9704–9709.
Li, G., West, A.J. (2014) Evolution of Cenozoic seawater lithium isotopes: Coupling of global denudation regime and shifting seawater sinks. Earth and Planetary Science Letters 401, 284–293.
Li, S., Gaschnig, R.M., Rudnick, R.L. (2016) Insights into chemical weathering of the upper continental crust from the geochemistry of ancient glacial diamictites. Geochimica et Cosmochimica Acta 176, 96–117.
Liu, X.-M., Wanner, C., Rudnick, R.L., McDonough, W.F. (2015) Processes controlling δ7Li in rivers illuminated by study of streams and groundwaters draining basalts. Earth and Planetary Science Letters 409, 212–224.
McKenzie, N.R., Horton, B.K., Loomis, S.E., Stockli, D.F., Planavsky, N.J., Lee, C.-T.A. (2016) Continental arc volcanism as the principal driver of icehouse-greenhouse variability. Science 352, 444–447.
Melchin, M.J., Holmden, C., Williams, S.H. (2003) Correlation of graptolite biozones, chitinozoan biozones, and carbon isotope curves through the Hirnantian. Proceedings of the 9th International Symposium on the Ordovician System: INSUGEO, Serie Correlación Geológica.
Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
Misra, S., Froelich, P.N. (2012) Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science 335, 818–823.
Pogge von Strandmann, P.A.E., Burton, K.W., James, R.H., van Calsteren, P., Gislason, S.R., Mokadem, F. (2006) Riverine behaviour of uranium and lithium isotopes in an actively glaciated basaltic terrain. Earth and Planetary Science Letters 251, 134–147.
Pogge von Strandmann, P.A.E., James, R.H., van Calsteren, P., Gíslason, S.R., Burton, K.W. (2008) Lithium, magnesium and uranium isotope behaviour in the estuarine environment of basaltic islands. Earth and Planetary Science Letters 274, 462–471.
Pogge von Strandmann, P.A.E., Elliott, T., Marschall, H.R., Coath, C., Lai, Y.J., Jeffcoate, A.B., Ionov, D.A. (2011) Variations of Li and Mg isotope ratios in bulk chondrites and mantle xenoliths. Geochimica et Cosmochimica Acta 75, 5247–5268.
Pogge von Strandmann, P.A.E., Jenkyns, H.C., Woodfine, R.G. (2013) Lithium isotope evidence for enhanced weathering during Oceanic Anoxic Event 2. Nature Geoscience 6, 668–672.
Pogge von Strandmann, P.A.E., Frings, P.J., Murphy, M.J. (2017) Lithium isotope behaviour during weathering in the Ganges Alluvial Plain. Geochimica et Cosmochimica Acta 198, 17–31.
Pohl, A., Donnadieu, Y., Le Hir, G., Ladant, J.-B., Dumas, C., Alvarez-Solas, J., Vandenbroucke, T.R.A. (2016) Glacial onset predated Late Ordovician climate cooling. Paleoceanography 31, 800–821.
Sauzeat, L., Rudnick, R.L., Chauvel, C., Garcon, M., Tang, M. (2015) New perspectives on the Li isotopic composition of the upper continental crust and its weathering signature. Earth and Planetary Science Letters 428, 181–192.
Shields, G.A., Carden, G.A.F., Veizer, J., Meidla, T., Rong, J.-Y., Li, R.-Y. (2003) Sr, C, and O isotope geochemistry of Ordovician brachiopods: A major isotopic event around the Middle-Late Ordovician transition Geochimica et Cosmochimica Acta 67, 2005–2025.
Tessier, A., Campbell, P.G.C., Bisson, M. (1979) Sequential Extraction Procedure for the Speciation of Particulate Trace Metals. Analytical Chemistry 51, 844-851.
Underwood, C.J., Crowley, S.F., Marshall, J.D., Brenchley, P.J. (1997) High-resolution carbon isotope stratigraphy of the basal Siluarian stratotype (Dob's Linn, Scotland) and its global correlation. Journal of the Geological Society 154, 709–718.
Wanner, C., Bucher, K., Pogge von Strandmann, P.A.E., Niklaus Waber, H., Pettke, T. (2017) On the use of Li isotopes as a proxy for water–rock interaction in fractured crystalline rocks: A case study from the Gotthard rail base tunnel. Geochimica Et Cosmochimica Acta 198, 396–418.
Williams, S.H. (1983) The Ordovician–Silurian boundary graptolite fauna of Dob's Linn, southern Scotland. Palaeontology 26, 605–639.
Williams, S.H. (1986) Top Ordovician and lowest Silurian of Dob's Linn. Geology Society of London Special Publication 20, 165–171.
Williams, S.H. (1988) Dob's Linn—the Ordovician–Silurian boundary stratotype. In: Cocks, L.R.M., Rickards, R.B. (Eds.) A Global Analysis of the Ordovician-Silurian Boundary. Bulletin of the British Museums (Natural History) Geology Series 43, 17–30.
Young, S.A., Saltzman, M.R., Foland, K.A., Linder, J.S., Kump, L.R. (2009) A major drop in seawater 87Sr/86Sr during the Middle Ordovician (Darriwilian): Links to volcanism and climate? Geology 37, 951–954.
Figures and Tables
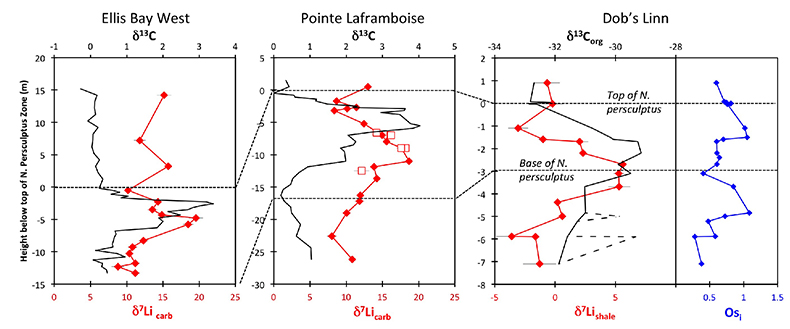
Figure 1 Carbonate (Pointe Laframboise and Ellis Bay West) and shale (Dob’s Linn) Li isotope ratios. Open squares are separately analysed brachiopods. Carbon and osmium (initial 187Os/188Os) isotope data are from the same samples (Finlay et al., 2010
Finlay, A.J., Selby, D., Grocke, D.R. (2010) Tracking the Hirnantian glaciation using Os isotopes. Earth and Planetary Science Letters 293, 339–348.
). Biostratigraphic correlation is based on the N. persculptus Zone (Melchin et al., 2013Melchin, M.J., Mitchell, C.E., Holmden, C., Storch, P. (2013) Environmental changes in the Late Ordovician-early Silurian: Review and new insights from black shales and nitrogen isotopes. Geological Society of America Bulletin 125, 1635–1670.
).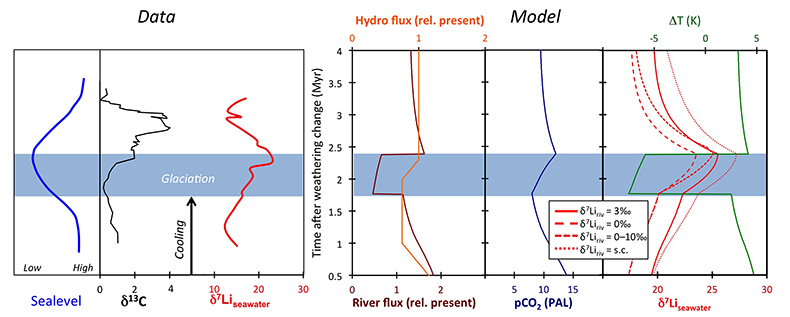
Figure 2 Comparison of data and model results. Sea level timing is from stratigraphic data (Ghienne et al., 2014
Ghienne, J.-F., Desrochers, A., Vandenbroucke, T.R.A., Achab, A., Asselin, E., Dabard, M.-P., Farley, C., Loi, A., Paris, F., Wickson, S., Veizer, J. (2014) A Cenozoic-style scenario for the end-Ordovician glaciation. Nature Communications 5, doi: 10.1038/ncomms5485.
). Seawater Li isotope data were generated from carbonate data by adding a 4 ‰ fractionation factor (Marriott et al., 2004Marriott, C.S., Henderson, G.M., Crompton, R., Staubwasser, M., Shaw, S. (2004) Effect of mineralogy, salinity, and temperature on Li/Ca and Li isotope composition of calcium carbonate. Chemical Geology 212, 5–15.
). The model shows the changes in riverine and hydrothermal Li fluxes, the pCO2 levels and temperature anomalies caused by these changes, and the resulting oceanic δ7Li curve. The red model lines are for scenarios where riverine δ7Li = 3 ‰, 0 ‰, a change from 0 to 10 ‰ during the glaciation and “shale-constrained” (s.c.), using Dob’s Linn δ7Li data to constrain river values (see text and Supplementary Information for detail).Back to article
Supplementary Figures and Tables
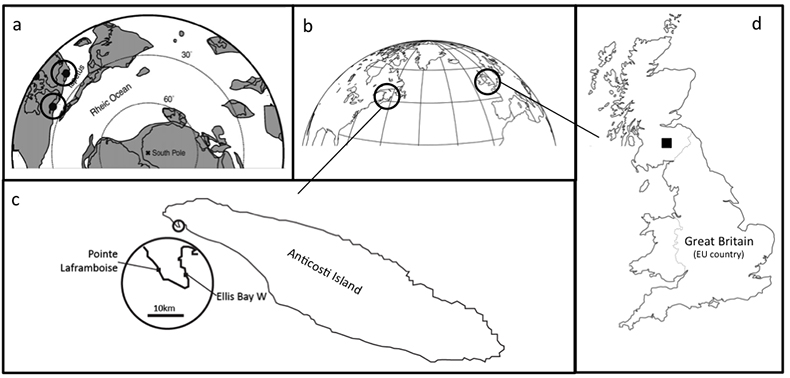
Figure S-1 Sample location maps. (a) Palaeogeographic location map, with sample locations highlighted (adapted from Finlay et al., 2010); (b) Current geography of sample locations from Scotland and Anticosti Island; (c) Detail of sample locations on Anticosti Island; (d) Detail of sample location of Dob’s Linn.
Table S-1 Li isotope and trace element data from the section studies here.
| Height | δ7Li | 2 sd | Li/Ca | Mg/Ca | Al/Ca | Mn/Ca | Sr/Ca | |
| m | µmol/mol | mmol/mol | mmol/mol | mmol/mol | mmol/mol | |||
| Point Laframboise | ||||||||
| L-M-54 | 180.8 | 10.8 | 0.1 | 11.1 | 34.6 | 0.2 | 2.1 | 2.3 |
| L-M-56 | 184.4 | 8.0 | 0.7 | 17.5 | 46.5 | 0.5 | 2.7 | 1.0 |
| L-M-58 | 188 | 10.1 | 0.2 | 18.5 | 43.2 | 0.4 | 2.7 | 2.8 |
| L-M-60 | 189.8 | 11.8 | 0.7 | 46.3 | 61.6 | 0.2 | 3.6 | 1.2 |
| L-M-61 | 190.7 | 11.9 | 0.4 | 30.5 | 41.6 | 0.6 | 3.4 | 1.2 |
| L-M-64 | 193.3 | 14.2 | 0.1 | 11.8 | 27.8 | 0.2 | 2.3 | 0.9 |
| L-M-66 | 195.1 | 13.8 | 0.1 | 12.4 | 26.3 | 0.3 | 5.3 | 1.2 |
| L-M-67 | 196 | 18.7 | 0.5 | 33.6 | 413.7 | 0.6 | 8.9 | 1.2 |
| PL-5i | 198 | 17.6 | 0.7 | 23.2 | 297.8 | 0.4 | 8.5 | 1.3 |
| L-M-69 | 199 | 15.6 | 0.1 | 13.1 | 96.9 | 0.2 | 3.1 | 1.0 |
| PL-8i | 200 | 14.9 | 0.7 | 10.2 | 376.3 | 0.2 | 7.4 | 1.1 |
| PL-13i | 201.8 | 12.4 | 0.1 | 17.9 | 47.5 | 0.3 | 2.3 | 1.4 |
| PL-17Bi | 203.8 | 8.4 | 0.2 | 12.1 | 31.8 | 0.2 | 3.5 | 0.7 |
| PL-18i | 204.1 | 10.2 | 0.6 | 5.0 | 63.4 | 0.1 | 3.0 | 1.1 |
| PL-19Ai | 204.3 | 11.4 | 0.2 | 20.7 | 15.6 | 0.2 | 1.2 | 0.6 |
| PL-22i | 205.3 | 8.7 | 0.1 | 9.0 | 30.1 | 0.1 | 3.7 | 0.9 |
| PL-27i | 207.5 | 13.0 | 0.3 | 11.7 | 24.7 | 0.3 | 1.8 | 1.2 |
| Large fossils | ||||||||
| 194.5 | 12.1 | 1.1 | 10.2 | 31.2 | 0.1 | 2.1 | 1.2 | |
| 198 | 18.2 | 0.4 | 20.5 | 42.8 | 0.2 | 2.6 | 1.4 | |
| 198 | 17.6 | 0.6 | 23.2 | 24.3 | 0.2 | 3.1 | 1.3 | |
| 200 | 16.1 | 0.4 | 20.7 | 28.9 | 0.1 | 4.4 | 1.0 | |
| 200 | 16.2 | 0.3 | 21.4 | 41.6 | 0.1 | 3.4 | 0.9 | |
| 200.4 | 14.2 | 0.3 | 15.1 | 38.0 | 0.1 | 2.9 | 1.0 | |
| Ellis Bay West | ||||||||
| E-M-1 | 0 | 11.2 | 0.6 | 44.0 | 88.2 | 0.2 | 4.2 | 1.3 |
| E-M-3 | 1 | 8.8 | 0.9 | 25.0 | 54.6 | 0.5 | 3.5 | 1.0 |
| E-M-4 | 1.5 | 11.2 | 0.6 | 20.6 | 82.9 | 0.1 | 0.8 | 1.2 |
| E-M-7 | 3 | 10.4 | 0.1 | 33.1 | 113.1 | 0.4 | 0.9 | 1.6 |
| E-M-9 | 4 | 10.8 | 0.6 | 20.9 | 63.4 | 0.0 | 0.7 | 1.0 |
| E-M-11 | 5 | 12.3 | 0.6 | 14.7 | 43.6 | 0.0 | 0.6 | 0.8 |
| E-M-16 | 7.5 | 18.5 | 0.7 | 26.1 | 237.2 | 0.4 | 1.2 | 1.3 |
| E-M-18 | 8.5 | 19.6 | 1.0 | 13.5 | 318.1 | 0.2 | 6.7 | 1.0 |
| E-M-19 | 9 | 14.8 | 0.6 | 11.7 | 57.6 | 0.1 | 3.0 | 1.3 |
| E-M-21 | 9.8 | 13.5 | 0.7 | 5.0 | 12.3 | 0.4 | 0.3 | 0.7 |
| E-M-25 | 11 | 14.3 | 0.2 | 38.0 | 155.6 | 0.3 | 3.7 | 1.1 |
| E-M-31 | 12.8 | 10.2 | 0.5 | 8.5 | 23.5 | 0.5 | 0.7 | 1.0 |
| E-M-35 | 16.5 | 15.7 | 0.4 | 10.4 | 26.3 | 0.0 | 1.1 | 1.2 |
| E-M-39 | 20.5 | 11.8 | 0.8 | 9.5 | 29.2 | 0.4 | 0.2 | 1.2 |
| E-M-46 | 27.5 | 15.2 | 1.0 | 11.3 | 26.4 | 0.3 | 0.2 | 1.3 |
| Dob's Linn | ||||||||
| AF20-07 | 0.9 | -0.7 | 1.1 | |||||
| DS2-04 | -0.03 | -0.2 | 0.9 | |||||
| AF07-07 | -1.1 | -3.1 | 0.8 | |||||
| AF32-07 | -1.6 | -1.0 | 0.4 | |||||
| AF23-07 | -1.7 | 2.0 | 0.7 | |||||
| AF24-07 | -2.2 | 2.3 | 0.3 | |||||
| AF26-07 | -2.7 | 5.6 | 0.3 | |||||
| AF27-07 | -3.1 | 5.3 | 0.4 | |||||
| AF11-07 | -3.69 | 5.3 | 0.9 | |||||
| AF12-07 | -4.38 | 0.2 | 0.2 | |||||
| AF29-07 | -5 | 0.6 | 0.3 | |||||
| AF15-07 | -5.88 | -3.6 | 1.3 | |||||
| AF30-07 | -5.9 | -1.6 | 0.4 | |||||
| AF31-07 | -7.1 | -1.3 | 1.4 | | ||||
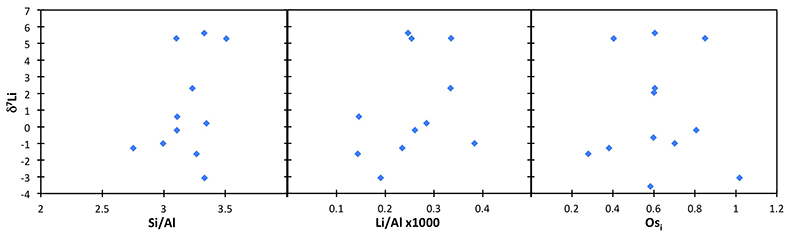
Figure S-2 Lack of correlation between δ7Li and grain size tracer Si/Al, and provenance tracers Li/Al and Os (Osi = 187Os/188Os) isotopes.
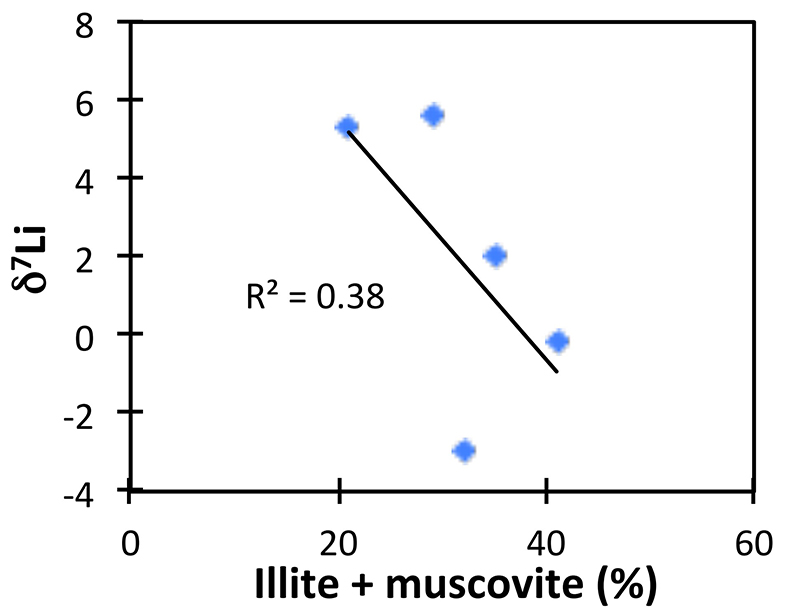
Figure S-3 Lack of significant correlation between shale δ7Li and secondary mineralogy.
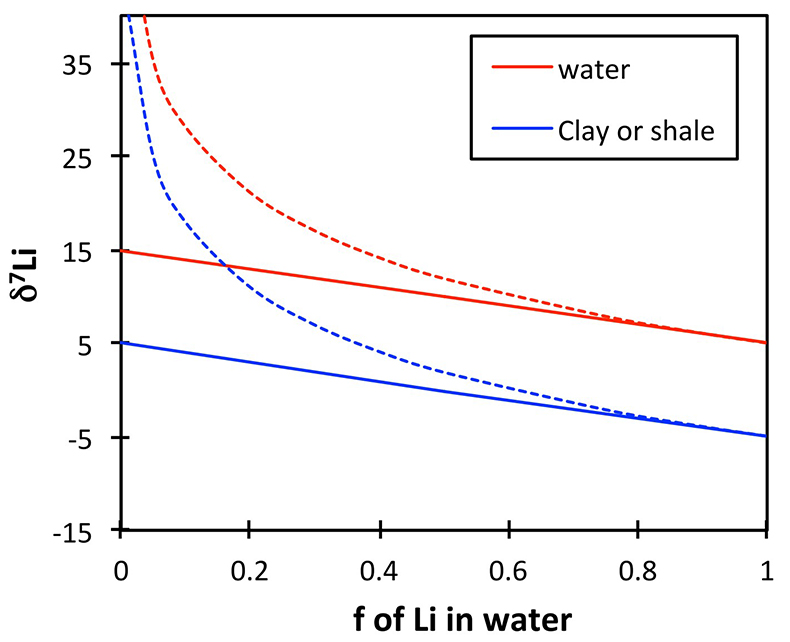
Figure S-4 Example of isotope fractionation behaviour of two linked phases (in this case water and clay) for a constant fractionation factor. Solid lines represent equilibrium fractionation, while dotted lines represent Rayleigh fractionation.
Table S-2 XRF major element concentration data (in wt. %) for the shales.
| Al2O3 | SiO2 | TiO2 | Fe2O3 | MnO | MgO | CaO | Na2O | K2O | P2O5 | |
| AF-32-07 | 19.44 | 66.01 | 0.78 | 7.27 | 0.71 | 3.37 | 0.22 | 0.78 | 3.30 | 0.14 |
| AF-27-07 | 10.84 | 43.13 | 0.53 | 6.02 | 1.07 | 6.07 | 8.16 | 0.35 | 2.04 | 0.08 |
| AF-12-07 | 14.87 | 56.44 | 0.85 | 2.78 | 0.01 | 1.38 | 0.29 | 0.28 | 4.14 | 0.03 |
| AF-07-07 | 14.52 | 54.85 | 0.80 | 6.16 | 0.11 | 2.63 | 0.22 | 0.41 | 3.03 | 0.11 |
| DS2-04 | 17.12 | 60.33 | 0.66 | 8.46 | 0.02 | 3.25 | 0.00 | 2.77 | 3.03 | 0.05 |
| AF-30-07 | 13.76 | 50.98 | 0.68 | 6.56 | 0.04 | 2.69 | 0.19 | 0.66 | 2.86 | 0.06 |
| AF-04-07 | 14.47 | 53.62 | 0.67 | 4.91 | 0.02 | 2.34 | 0.10 | 1.01 | 3.17 | 0.04 |
| AF-24-07 | 13.74 | 50.38 | 0.67 | 4.91 | 0.54 | 4.57 | 5.38 | 0.34 | 2.85 | 0.16 |
| AF-31-07 | 19.79 | 61.79 | 0.84 | 7.95 | 0.10 | 3.93 | 0.31 | 0.81 | 3.53 | 0.06 |
| AF-11-07 | 15.27 | 53.75 | 0.78 | 2.70 | 0.02 | 1.51 | 0.34 | 0.30 | 3.97 | 0.04 |
| AF-26-07 | 12.30 | 46.45 | 0.63 | 5.01 | 0.56 | 4.21 | 5.18 | 0.25 | 2.60 | 0.10 |
| AF-29-07 | 19.13 | 67.47 | 0.76 | 6.13 | 0.04 | 3.62 | 0.25 | 0.97 | 3.39 | 0.07 |
Table S-3 Quantitative mineralogy data from some of the shale samples.
| Siroquant Quantitative Analysis | AF0406 | DS104 | AF0807 | AF23A07 | AF26A07 | AF27A07 |
| (wt. %) | ||||||
| Anhydrite | - | - | - | - | - | - |
| Ankerite | - | - | - | 6 | 17 | 30 |
| Calcite | - | - | - | 3 | 3 | 1 |
| Chlorite | - | 12 | 7 | 10 | 8 | 7 |
| Dolomite | 1 | - | - | - | - | - |
| Gypsum | - | - | - | - | - | - |
| Illite/Muscovite | 36 | 41 | 32 | 35 | 29 | 21 |
| Kaolinite | 9 | 3 | 2 | - | 3 | 2 |
| K-Feldspar | 3 | - | - | - | - | - |
| Plagioclase | 1 | 7 | 12 | 10 | 8 | 8 |
| Pyrite | 7 | 5 | 2 | - | - | 1 |
| Quartz | 43 | 32 | 45 | 36 | 32 | 30 |
Table S-4 Results of sequential leaching of some of the Dob’s Linn shales.
| δ7Li | 2 sd | % of bulk Li | |
| AF23-07 | |||
| Exchangeable | 13.1 | 0.6 | 1.5 |
| Carbonate | 8.6 | 0.3 | 3.5 |
| Residue | 2.7 | 0.2 | 95 |
| Bulk | 2.0 | 0.7 | |
| AF11-07 | |||
| Exchangeable | 15.6 | 0.6 | 0.8 |
| Carbonate | 14.3 | 1.0 | 2.2 |
| Residue | 4.7 | 0.1 | 97 |
| Bulk | 5.3 | 0.9 | |
| AF15-07 | |||
| Exchangeable | 1.5 | 0.5 | 2 |
| Carbonate | -3.0 | 0.5 | 4 |
| Residue | -2.5 | 0.4 | 94 |
| Bulk | -3.6 | 1.3 | |
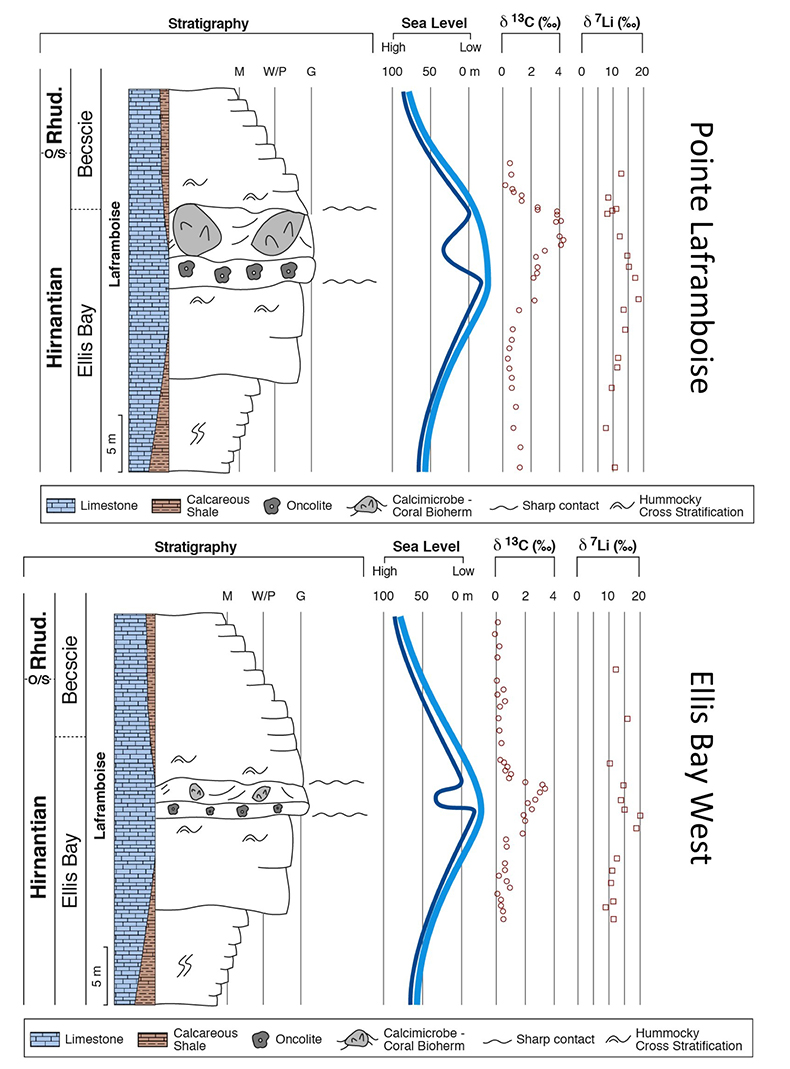
Figure S-5 Anticosti section lithology (Desrochers et al., 2010; Achab et al., 2011, 2013; Copper et al., 2013), compared to isotope data.
Table S-5 Definitions of parameters used in the models.
| Symbol | Parameter |
| A | Ocean-atmosphere reservoir of DIC/CO2 (mol) |
| A0 | Modern reservoir (mol) |
| Fd | Degassing flux of CO2 input (mol) |
| Fw | Silicate weathering flux of CO2 consumption (mol) |
| D | Normalised degassing parameter |
| U | Normalised uplift parameter |
| kV | Fraction of present weathering rate in the absence of plants |
| ∆T | Temperature change (K) |
| Lithium | |
| Fr | Riverine Li flux |
| Fh | Hydrothermal Li flux |
| Fsed | Removal of Li into ocean secondary sediments |
| R | Isotope ratio |
| N | Ocean reservoir of Li (mol) |
| kLi | Partition coefficient of oceanic Li sink |
| kh | Modern hydrothermal Li input (mol) |
| kw | Modern riverine Li input (mol) |
| ∆sink | Li isotopic fractionation factor imposed by the Li sink |
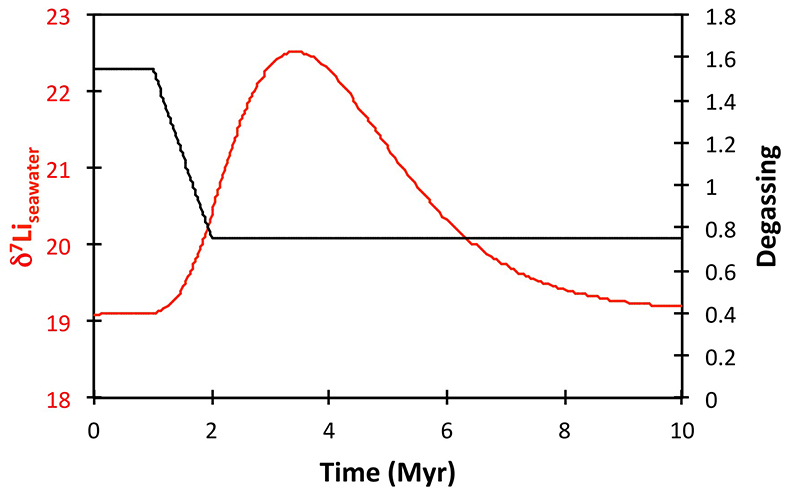
Figure S-6 Result of a permanent decrease in degassing on the Li isotope composition of the oceans. Note that this scenario assumes Rr = 3 ‰.
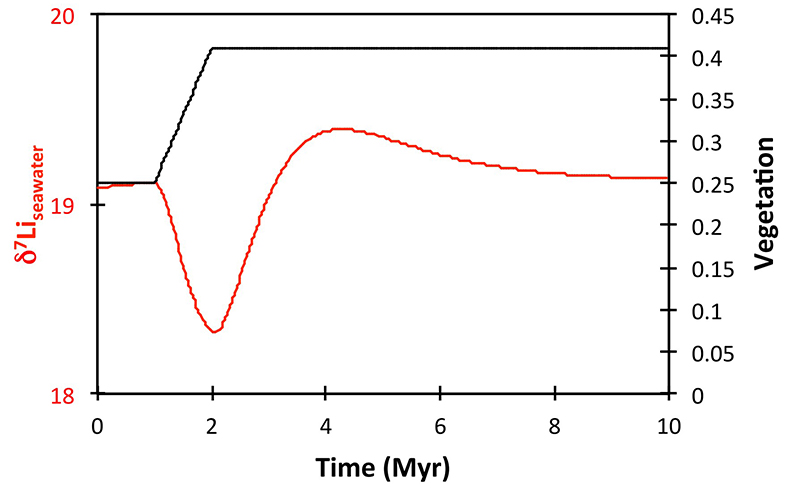
Figure S-7 Result of a permanent increase in vegetation cover on the Li isotope composition of the oceans. Note that this scenario assumes Rr = 3 ‰.
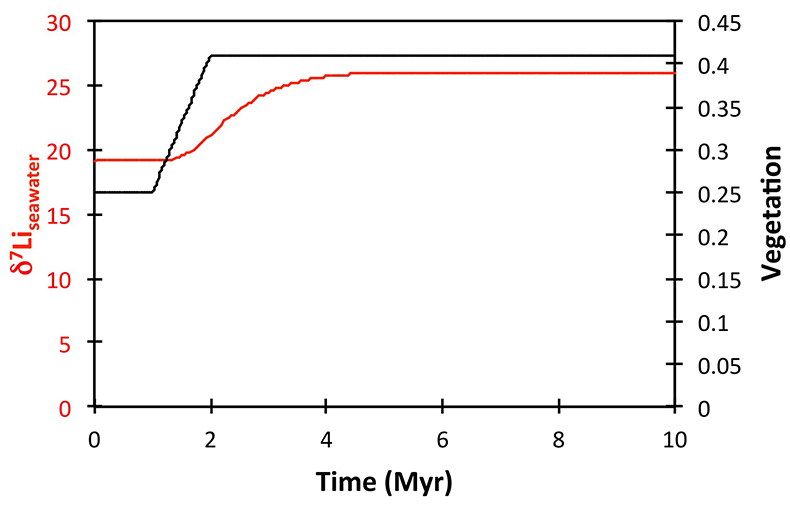
Figure S-8 Result of a permanent increase in vegetation cover combined with an increase in riverine δ7Li on the Li isotope composition of the oceans.
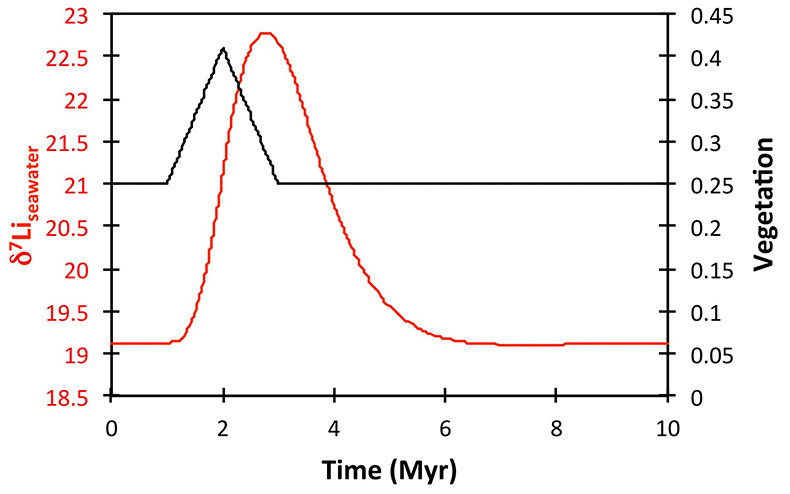
Figure S-9 Identical scenario to Figure S-8 (increase in vegetation cover combined with an increase in riverine δ7Li), but combined with a subsequent decrease in kv and Rr.
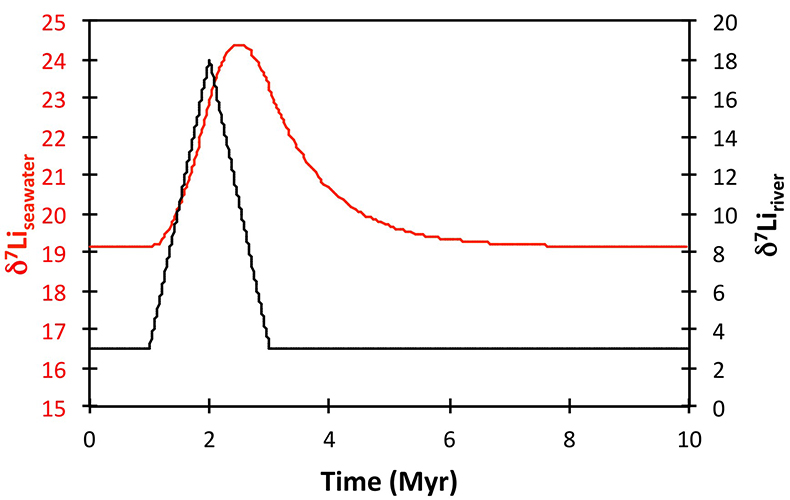
Figure S-10 A scenario where the seawater δ7Li excursion is solely caused by a change in river δ7Li (Rr) (but there is no associated change in the modelled carbon cycle and global temperature).

Figure S-11 Effect of an oscillatory system from the feedbacks described in the text on the relative temperature and seawater δ7Li values.
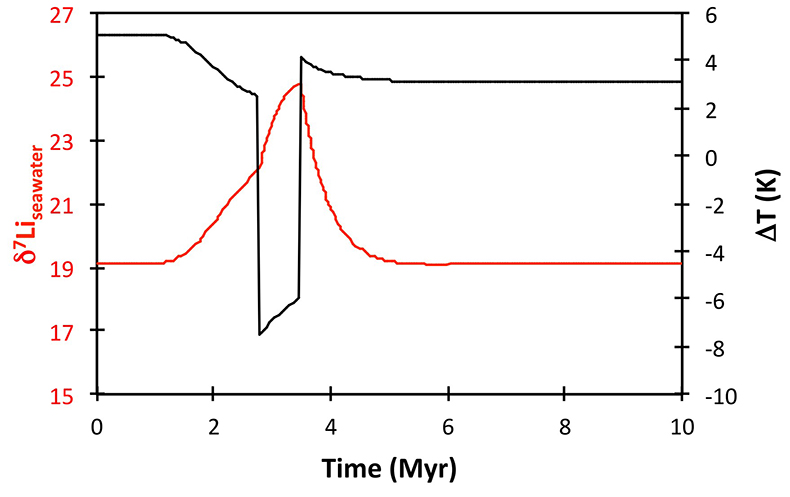
Figure S-12 Effect of single glaciation on the relative temperature and seawater δ7Li values.
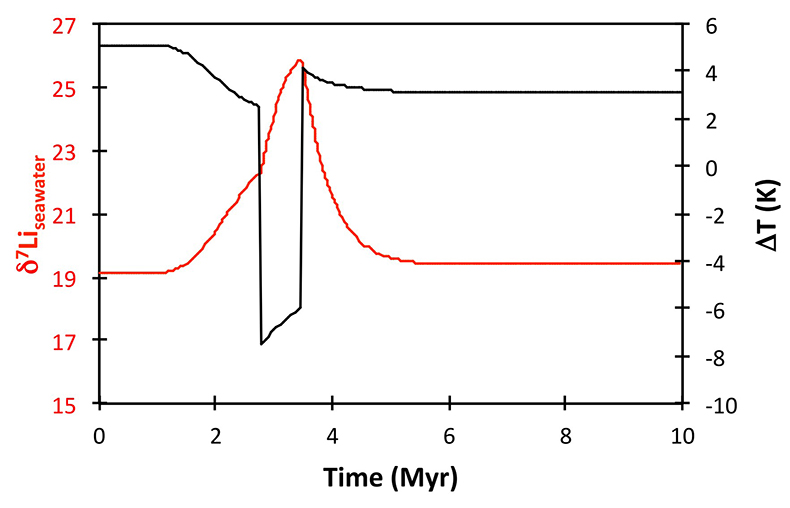
Figure S-13 The same scenario as in Figure S-12, but with an added temperature control on the fractionation factor of the Li sink.
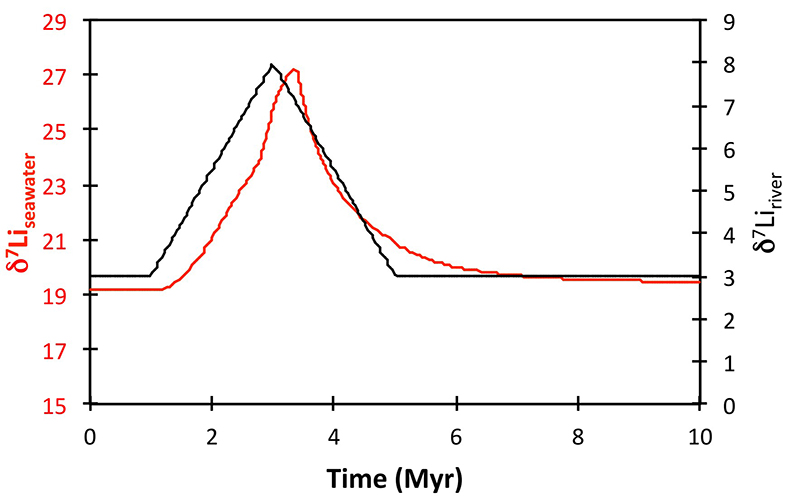
Figure S-14 The same scenario as in Figure S-13, except that riverine δ7Li also increases.
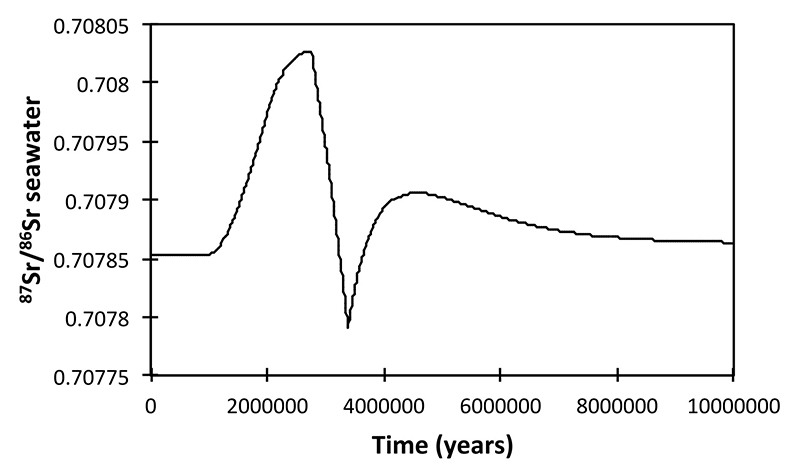
Figure S-15 Modelled Sr isotope ratio of seawater, using factors taken from the Li-C model.