A stable isotope doping method to test the range of applicability of detailed balance
Affiliations | Corresponding Author | Cite as- Share this article





-
Article views:9,378Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract
Wegscheider, R. (1901) Über simultane Gleichgewichte und die Beziehungen zwischen Thermodynamik und Reactionskinetik homogener Systeme. Monatshefte für Chemie / Chemical Monthly 32, 849–906.
; Lewis, 1925Lewis, G.N. (1925) A new principle of equilibrium. Proceedings of the National Academy of Sciences of the United States of America 11, 179-183.
; Onsager, 1931Onsager, L. (1931) Reciprocal relations in irreversible processes. I. Physical Review 37, 405-426.
), and its wide application in geochemistry has mostly been implicit and without experimental testing of its applicability. Nevertheless, many extrapolations based on PDB without experimental validation have far reaching impacts on society’s mega environmental enterprises. Here we report an isotope doping method that independently measures simultaneous dissolution and precipitation rates and can test this principle. The technique reacts a solution enriched in a rare isotope of an element with a solid having natural isotopic abundances (Beck et al., 1992Beck, J.W., Berndt, M.E., Seyfried Jr, W.E. (1992) Application of isotopic doping techniques to evaluation of reaction kinetics and fluid/mineral distribution coefficients: An experimental study of calcite at elevated temperatures and pressures. Chemical Geology 97, 125-144.
; Gaillardet, 2008Gaillardet, J. (2008) Isotope geochemistry as a tool for deciphering kinetics of water-rock interaction, in: Brantley, S.L., Kubicki, J.D., White, A.F. (Eds.) Kinetics of Water-Rock Interaction. Springer, New York.
; Gruber et al., 2013Gruber, C., Harpaz, L., Zhu, C., Bullen, T.D., Ganor, J. (2013) A new approach for measuring dissolution rates of silicate minerals by using silicon isotopes. Geochimica et Cosmochimica Acta 104, 261-280.
). Dissolution and precipitation rates are found from the changing isotopic ratios. Our quartz experiment doped with 29Si showed that the equilibrium dissolution rate remains unchanged at all degrees of undersaturation. We recommend this approach to test the validity of using the detailed balance relationship in rate equations for other substances.Figures and Tables
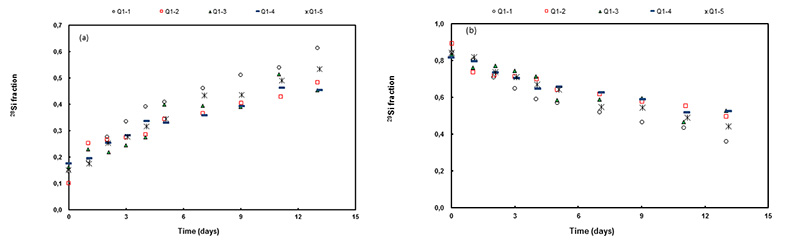
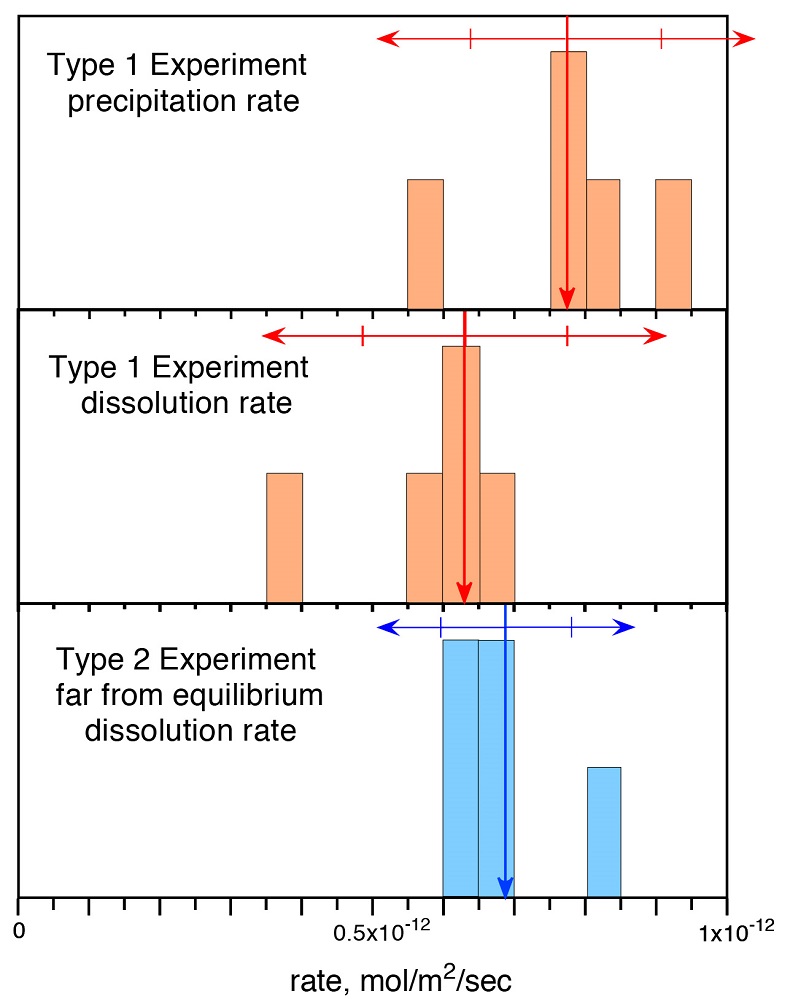
 Figure 1 Si isotope fractional abundances in experimental solutions over time. The solution was saturated with quartz and doped with nearly 100 % 29Si. The first sample was taken after 15 minutes. The increase of 28Si concentration (fractional abundance times dissolved elemental Si concentration) is due to the dissolution of quartz while the decrease of 29Si abundances and concentrations is due to the precipitation of quartz. The reaction rates given in Table 1 are based on the slopes of the trends extrapolated to zero time. |  Table 1 Rate of quartz dissolution and precipitation at equilibrium based on the rate of appearance of 28Si and disappearance of 29Si respectively, and the far from equilibrium dissolution rate for solutions containing no dissolved silica. | 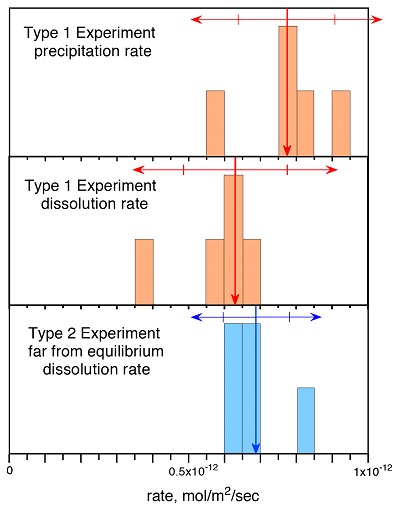 Figure 2 Comparison of the equilibrium dissolution and precipitation rates determined using 29Si isotope doping (Type 1 Experiment) with the far from equilibrium dissolution rate (Type 2 Experiment). The vertical arrow points to the average value for each set of experiments and the horizontal arrows indicate two standard deviations of the data. |
| Figure 1 | Table 1 | Figure 2 |
top
Introduction
The principle of detailed balance (PDB) arose from statistical and quantum mechanics in the early twentieth century to become a foundation of modern chemical kinetics (Wegscheider, 1901
Wegscheider, R. (1901) Über simultane Gleichgewichte und die Beziehungen zwischen Thermodynamik und Reactionskinetik homogener Systeme. Monatshefte für Chemie / Chemical Monthly 32, 849–906.
; Lewis, 1925Lewis, G.N. (1925) A new principle of equilibrium. Proceedings of the National Academy of Sciences of the United States of America 11, 179-183.
; Onsager, 1931Onsager, L. (1931) Reciprocal relations in irreversible processes. I. Physical Review 37, 405-426.
), but its appropriate application to chemical kinetics is obscure because it is difficult to use conventional rate experiments to determine independently the forward and reverse rates at equilibrium. As a result, experimental tests of the range of PDB applicability have largely been absent in geochemistry with only a few tests reported in the chemistry, physics, and chemical engineering literature.The principle states that at equilibrium, the rates of forward and reverse reaction rates are equal (Lasaga, 1998
Lasaga, A.C. (1998) Kinetic Theory in the Earth Sciences. Princeton University Press, New York.
, p.82). When PDB is applicable, the following relationship holds,Eq. 1
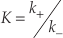
where K denotes the equilibrium constant, k+ and k- stand for the rate constants for forward and reverse reactions, respectively. Equation 1 is a powerful link between thermodynamics and kinetics (Lasaga, 1998
Lasaga, A.C. (1998) Kinetic Theory in the Earth Sciences. Princeton University Press, New York.
), and a device by which measurements of rate constants for reactions in one direction may be used to obtain the rate constants for the experimentally inaccessible reverse directions (Mahan, 1975Mahan, B.H. (1975) Microscopic reversibility and detailed balance - analysis. Journal of Chemical Education 52, 299-302.
). This relies on the assumption that k+ and k- do not change when the reaction departs from equilibrium.Rimstidt and Barnes (1980)
Rimstidt, J.D., Barnes, H.L. (1980) The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta 44, 1683-1699.
used this principle to obtain both k- and k+ from quartz dissolution data only. In their widely used kinetic data compilation, Palandri and Kharaka (2004)Palandri, J.L., Kharaka, Y.K. (2004) A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling., U.S. Geological Survey Open File Report 2004-1068, 66.
stated that “Precipitation rate data do not exist for most minerals…”. “Therefore, we use the principle of microscopic reversibility… where the precipitation rate constant can be calculated from the dissolution rate constant and the equilibrium constant.”The most important and far reaching application of PDB in geology is in the so called “transition state theory rate law” or “linear rate law”, which expresses mineral dissolution rates as a function of chemical potential (or affinity) (Lasaga, 1981
Lasaga, A.C. (1981) Rate laws of chemical reactions. In: Lasaga, A.C., Kirkpatrick, R.J. (Ed.) Kinetics of Geochemical Processes. Mineralogical Society of America, Washington DC, 1-68.
; Aagaard and Helgeson, 1982Aagaard, P., Helgeson, H.C. (1982) Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. I. Theoretical considerations. American Journal of Science 282, 237-285.
),Eq. 2
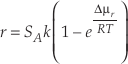
where r denotes the net rate of chemical reaction, and SA the surface area. Δµr stands for the chemical potential of the reaction, R the gas constant, and T temperature in Kelvin.
Equation 2 assumes that the K = k+/k- relationship applies when the reaction is not at equilibrium (see Supplementary Information). Chemists have long known that “rate coefficients determined away from equilibrium are not necessarily the same as those at equilibrium, and their ratio is not necessarily equal to Kc” (Laidler, 1987
Laidler, K.J. (1987) Chemical Kinetics. Third Edition, Prentice Hall, New York.
).Despite the scepticism expressed by experts and a growing literature describing experiments at near equilibrium that show deviations from this relationship in Equation 2 (see review by Zhu, 2009
Zhu, C. (2009) Geochemical modeling of reaction paths and geochemical reaction networks. Reviews in Mineralogy & Geochemistry 70, 533-569.
), this rate law has been widely used in scientific and technological situations, such as the performance models for high-level radioactive waste disposal (Grambow, 1985Grambow, B. (1985) A general rate equation for nuclear waste glass corrosion. Materials Reserch Society Symposium Proceedings 44, 15-27.
) and geological CO2 sequestration (Johnson et al., 2004Johnson, J.W., Nitao, J.J., Knauss, K.G. (2004) Reactive transport modeling of CO2 storage in saline aquifers to elucidate fundamental processes, trapping mechanisms and sequestration partitioning. Geological Society of London, Special Publication 233, 107-128.
; Marini, 2007Marini, L. (2007) Geological Sequestration of Carbon Dioxide. Elsevier, Amsterdam.
). The operational periods of these repositories extend beyond 10,000 years and span geochemical conditions far from equilibrium to equilibrium. Failure of the detailed balance assumption would invalidate these important models (see Supplementary Information). Nevertheless, the ad hoc applications continue because of the lack of experimental techniques to test the valid range of extrapolation for the principle of detailed balance.Here we show that recent advancements in stable isotope analysis by MC-ICP-MS and enriched isotopic standards make it possible to use an isotope doping method to determine the simultaneous dissolution and precipitation rates independently at any degree of saturation so we can validate rate equations and also test the range of applicability of the principle of detailed balance. Although our isotope doping method is applicable to many solid dissolution reactions, we demonstrate it by reacting a saturated H429SiO4 aqueous solution with predominantly 28SiO2 (quartz).
Quartz makes up about 20 % of the earth’s continental crust and there are many implications for its rate of reaction with aqueous solutions. The simultaneous dissolution and precipitation reactions that occur as solids equilibrate with solution are typically modelled using a two-term rate equation. For example, quartz dissolves in water by the reaction
Eq. 3
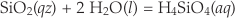
and the rate of change of silica concentration can be expressed as
Eq. 4
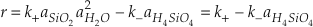
where the activities of SiO2 and H2O equal one. The two rate constants cannot be uniquely defined by measuring only the rate of change of elemental silica concentration. This problem is typically circumvented by using the principle of detailed balance to recast the rate equation in terms of one rate constant and the known equilibrium constant (K = k+/k-) (Rimstidt and Barnes, 1980
Rimstidt, J.D., Barnes, H.L. (1980) The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta 44, 1683-1699.
).Eq. 5
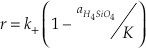
However, this approach is valid only if the rate-limiting step (and therefore k+ and k-) remains unchanged when the reaction departs from equilibrium. Etch pits (Brantley et al., 1986
Brantley, S.L., Crane, S.R., Crerar, D.A., Hellmann, R., Stallard, R. (1986) Dissolution at dislocation etch pits in quartz. Geochimica et Cosmochimica Acta 50, 2349-2361.
; Lüttge, 2006Lüttge, A. (2006) Crystal dissolution kinetics and Gibbs free energy. Journal of Electron Spectroscopy and Related Phenomena 150, 248-259.
) and “leached or re-precipitated layers” (Hellmann et al., 2003Hellmann, R., Penisson, J.-M., Hervig, R.L., Thomassin, J.-H., Abrioux, M.-F. (2003) An EFTEM/HRTEM high-resolution study of the near surface of labradorite feldspar altered at acid pH: evidence for interfacial dissolution-reprecipitation. Physics and Chemistry of Minerals 30, 192-197.
), which are not present at equilibrium, suggest that the extrapolation of equilibrium rate constants to highly undersaturated solutions may not be justified. Testing the applicable range for the PDB in cases affected by these and other complications will be difficult. Quartz was chosen for this test of the utility of the isotope doping method because there is good evidence that the PDB is valid over the entire range of undersaturation. Berger et al. (1994)Berger, G., Cadore, E., Schott, J., Dove, P.M. (1994) Dissolution rate of quartz in lead and sodium electrolyte solutions between 25 and 300°C: Effect of the nature of surface complexes and reaction affinity. Geochimica et Cosmochimica Acta 58, 541-551.
showed that quartz dissolution rates fit Equation 5 and Rimstidt and Barnes (1980)Rimstidt, J.D., Barnes, H.L. (1980) The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta 44, 1683-1699.
showed that they also fit Equation 4.top
Methods
We tested the validity of Equations 4 and 5 using a stable isotope doping experiment. The silicon in quartz has three stable isotopes and the natural quartz used in our experiments has an isotopic composition of 91.232 % 28Si, 5.410 % 29Si, and 3.3585 % 30Si. In our Type 1 equilibrium experiments a solution initially containing nearly ~100 % 29Si was maintained at or near equilibrium with quartz and sampled periodically to find the 28Si and 29Si concentrations. We used the initial rate method (Rimstidt, 2013
Rimstidt, J.D. (2013) Geochemical rate models: An introduction to geochemical kinetics. Cambridge University Press.
) to find the rate of appearance of 28Si in solution, which gives the dissolution rate at equilibrium, and the rate of disappearance of 29Si, which gives the precipitation rate at equilibrium. The Si isotope abundances in the experimental solutions evolved significantly over the course of experiments but the initial rate method determined the rate at zero time thereby avoiding complications associated with minor but measurable isotopic fractionation.Two types of experiments were carried out in this study. Type 1 experiments were conducted at equilibrium conditions where the solution was saturated with respect to quartz and Type 2 experiments were performed at far from equilibrium conditions where the initial solution contained no dissolved silica. Type 1 and Type 2 dissolution experiments were both batch reactor experiments conducted at 50 ± 1 °C. The starting solution for Type 1 experiments contained 340 μM 29SiO2, which is the solubility of quartz at 50 °C (Rimstidt, 1997
Rimstidt, J.D. (1997) Quartz solubility at low temperatures. Geochimica et Cosmochimica Acta 61, 2553-2558.
), and the solution was reacted with an ion exchange resin to remove cations that would catalyse the quartz dissolution rate. These solutions remained within ±0.3 kJ/mol of equilibrium throughout the experiments. The starting solution for the Type 2 dissolution experiments was deionised water. The pH of the starting solutions was near 5.5 for both types of experiment. More detailed analytical methods are described in the Supplementary Information section.top
Results
Figure 1 shows the fractional Si isotope concentrations versus time for the Type 1 equilibrium experiments and Table 1 gives the rates derived from all of the experiments. Figure 2 shows that the dissolution and precipitation rates are essentially the same, thus demonstrating that we have measured the dissolution rate constant at equilibrium. Furthermore, Figure 2 shows that the Type 2 far from equilibrium (no dissolved silica) dissolution rates (Q2 experiments) were essentially the same as the equilibrium (saturated solution) rates. The dissolved silica activity in the Type 2 experiments was zero for the initial rate. Inserting that value into either Equation 4 or 5 shows that the initial rate equals the dissolution rate constant. This means that the dissolution rate constant (k+) is the same at zero silica concentration as it is at equilibrium.

Figure 1 Si isotope fractional abundances in experimental solutions over time. The solution was saturated with quartz and doped with nearly 100 % 29Si. The first sample was taken after 15 minutes. The increase of 28Si concentration (fractional abundance times dissolved elemental Si concentration) is due to the dissolution of quartz while the decrease of 29Si abundances and concentrations is due to the precipitation of quartz. The reaction rates given in Table 1 are based on the slopes of the trends extrapolated to zero time.
Table 1 Rate of quartz dissolution and precipitation at equilibrium based on the rate of appearance of 28Si and disappearance of 29Si respectively, and the far from equilibrium dissolution rate for solutions containing no dissolved silica.
| Type 1 Equilibrium experiments | ||
| Experiment | Dissolution rate | Precipitation rate |
| mol/m2/sec | mol/m2/sec | |
| Q1-1 | 7.05 × 10-13 | 8.40 × 10-13 |
| Q1-2 | 6.83 × 10-13 | 7.75 × 10-13 |
| Q1-3 | 7.65 × 10-13 | 9.39 × 10-13 |
| Q1-4 | 3.95 × 10-13 | 5.64 × 10-13 |
| Q1-5 | 6.12 × 10-13 | 7.51 × 10-13 |
| Average | 6.32 × 10-13 | 7.74 × 10-13 |
| ±std dev | ±1.43 × 10-13 | ±1.38 × 10-13 |
| Type 2 Far from equilibrium experiments | ||
| Q2-1 | 8.32 × 10-13 | |
| Q2-2 | 6.11 × 10-13 | |
| Q2-3 | 6.33 × 10-13 | |
| Q2-4 | 6.66 × 10-13 | |
| Q2-5 | 6.92 × 10-13 | |
| Average | 6.87 × 10-13 | |
| ±std dev | ±0.88 × 10-13 |

Figure 2 Comparison of the equilibrium dissolution and precipitation rates determined using 29Si isotope doping (Type 1 Experiment) with the far from equilibrium dissolution rate (Type 2 Experiment). The vertical arrow points to the average value for each set of experiments and the horizontal arrows indicate two standard deviations of the data.
top
Discussion and Conclusions
Our results show that k+ at zero silica concentration is the same as at equilibrium so we conclude that the k+ determined at equilibrium is valid at all degrees of undersaturation. This has important implications for predicting rates over a wide range of conditions as explained by Schott et al. (2009)
Schott, J., Pokrovsky, O.S., Oelkers, E.H. (2009) The link between mineral dissolution/precipitation kinetics and solution chemistry. Reviews in Mineralogy & Geochemistry 70, 207-258.
.Another application of our experimental results is the validation of equilibrium constants for quartz solubility. Rimstidt (1997)
Rimstidt, J.D. (1997) Quartz solubility at low temperatures. Geochimica et Cosmochimica Acta 61, 2553-2558.
measured quartz solubility at 25, 50, 75, and 96 oC in experiments up to 4917 days. These long-term experimental data formed the basis for establishing quartz solubility as a function of temperature, and also for deriving the standard thermodynamic properties for aqueous species H4SiO4(aq) (Rimstidt, 1997Rimstidt, J.D. (1997) Quartz solubility at low temperatures. Geochimica et Cosmochimica Acta 61, 2553-2558.
; Stefansson, 2001Stefansson, A. (2001) Dissolution of primary minerals of basalt in natural waters - I. Calculation of mineral solubilities from 0 degrees C to 350 degrees C. Chemical Geology 172, 225-250.
). However, all experiments approached the quartz solubility from undersaturation and the reverse experiments – precipitation from oversaturation is far more complicated experimentally. Applying Equation 1, we found that the log K value for reaction (3) at 50 oC in pure water is -3.50, which is within the experimental uncertainties in Rimstidt (1997)Rimstidt, J.D. (1997) Quartz solubility at low temperatures. Geochimica et Cosmochimica Acta 61, 2553-2558.
.Applying our isotope doping method to quartz reaction rates and solubility is an obvious first step, and the results are confirmatory rather than contradictory to experimental data from conventional methods, which give us confidence to apply the 29Si method used in this study to investigate reactions of the other silicate minerals. Experiments for multicomponent silicate minerals often involve changes of reaction schemes in response to departure from equilibrium (Beig and Lüttge, 2006
Beig, M.S., Lüttge, A. (2006) Albite dissolution kinetics as a function of distance from equilibrium: Implications for natural feldspar weathering. Geochimica et Cosmochimica Acta 70, 1402-1420.
), and a poorly understood “leached” or “re-precipitated” layer can be developed (Hellmann et al., 2003Hellmann, R., Penisson, J.-M., Hervig, R.L., Thomassin, J.-H., Abrioux, M.-F. (2003) An EFTEM/HRTEM high-resolution study of the near surface of labradorite feldspar altered at acid pH: evidence for interfacial dissolution-reprecipitation. Physics and Chemistry of Minerals 30, 192-197.
). Aluminium may inhibit dissolution (Oelkers et al., 1994Oelkers, E.H., Schott, J., Devidal, J.L. (1994) The effect of aluminum, pH, and chemical affinity on the rates of aluminosilicate dissolution reactions. Geochimica et Cosmochimica Acta 58, 2011-2024.
), and other non-equilibrium surface features may occur so that the far from equilibrium dissolution and precipitation reaction paths can involve different pathways. However, Zhu et al. (2014)Zhu, C., Liu, Z., Schaefera, A., Wang, C., Zhang, G., Gruber, C., Ganor, J., Georg, R.B. (2014) Silicon isotopes as a new method of measuring silicate mineral reaction rates at ambient temperature. Procedia of Earth and Planetary Sciences 10, 189-193.
showed that this method was promising to measure albite dissolution rates very close to equilibrium, and the interferences of secondary phase precipitation and isotope fractionation was negligible. Detailed investigation of these multicomponent silicate minerals that make up the majority of Earth’s crust is the logical next step.In theory, our isotope doping method can be applied to many solids to test the range of validity of the near equilibrium rate constants. ICP-MS technology eases the analytical problems associated with using this experimental design for a wide range of non-silicate minerals and solids using the increasing number of non-traditional stable isotopes (such as Mg, Fe, Li). Therefore, the application of this method is not limited to geochemistry, but can be used in chemistry, chemical engineering, and environmental sciences as well.
The utility of the principle of detailed balance does not only rest on predicting rate constants or equilibrium constants. Lasaga (1981)
Lasaga, A.C. (1981) Rate laws of chemical reactions. In: Lasaga, A.C., Kirkpatrick, R.J. (Ed.) Kinetics of Geochemical Processes. Mineralogical Society of America, Washington DC, 1-68.
gives examples of predicting rate laws, the Arrhenius pre-exponential constants, and activation energy. Our experiments on quartz show the potential for harnessing the power of PDB for obtaining more kinetic parameters in geochemistry. Equally important is that the legitimacy of the extrapolation of PDB rate constants now can be experimentally tested for reactions where the PDB extrapolation has been used to model geological and environmental processes without due reckoning of its applicability.top
Acknowledgements
All experiments were carried out at Indiana University, USA with exception of Si isotope analysis which was carried out at State Key Laboratory of Continental Dynamics at Northwest University in China. Financial support of this research was provided by the U.S. NSF grant EAR-1225733, and operational funds at the State Key Laboratory of Continental Dynamics. ZYL was supported by funds from Zhejiang University through their “985” project. We thank Eric Oelkers and two anonymous reviewers for their helpful suggestions.
Editor: Eric H. Oelkers
top
Author Contributions
JDR and CZ developed the concept, designed the study, interpreted the data, and wrote the manuscript. ZYL carried out the experiments, YLZ participated in the interpretation of the data, and HLY developed method and performed the Si isotope analysis.
top
References
Aagaard, P., Helgeson, H.C. (1982) Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. I. Theoretical considerations. American Journal of Science 282, 237-285.
 Show in context
Show in context The most important and far reaching application of PDB in geology is in the so called “transition state theory rate law” or “linear rate law”, which expresses mineral dissolution rates as a function of chemical potential (or affinity) (Lasaga, 1981; Aagaard and Helgeson, 1982),
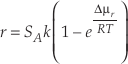
where r devotes the rate of chemical reaction, and SA the surface area. Δµr stands for the chemical potential of the reaction, R the gas constant, and T temperature in Kelvin.
View in article
Beck, J.W., Berndt, M.E., Seyfried Jr, W.E. (1992) Application of isotopic doping techniques to evaluation of reaction kinetics and fluid/mineral distribution coefficients: An experimental study of calcite at elevated temperatures and pressures. Chemical Geology 97, 125-144.
 Show in context
Show in context The technique reacts a solution enriched in a rare isotope of an element with a solid having natural isotopic abundances (Beck et al., 1992; Gaillardet, 2008; Gruber et al., 2013).
View in article
Beig, M.S., Lüttge, A. (2006) Albite dissolution kinetics as a function of distance from equilibrium: Implications for natural feldspar weathering. Geochimica et Cosmochimica Acta 70, 1402-1420.
 Show in context
Show in context Experiments for multicomponent silicate minerals often involve changes of reaction schemes in response to departure from equilibrium (Beig and Lüttge, 2006), and a poorly understood “leached” or “re-precipitated” layer can be developed (Hellmann et al., 2003).
View in article
Berger, G., Cadore, E., Schott, J., Dove, P.M. (1994) Dissolution rate of quartz in lead and sodium electrolyte solutions between 25 and 300°C: Effect of the nature of surface complexes and reaction affinity. Geochimica et Cosmochimica Acta 58, 541-551.
 Show in context
Show in context Berger et al. (1994) showed that quartz dissolution rates fit Equation 5 and Rimstidt and Barnes (1980) showed that they also fit Equation 4.
View in article
Brantley, S.L., Crane, S.R., Crerar, D.A., Hellmann, R., Stallard, R. (1986) Dissolution at dislocation etch pits in quartz. Geochimica et Cosmochimica Acta 50, 2349-2361.
 Show in context
Show in context Etch pits (Brantley et al., 1986; Lüttge, 2006) and “leached or re-precipitated layers” (Hellmann et al., 2003), which are not present at equilibrium, suggest that the extrapolation of equilibrium rate constants to highly undersaturated solutions may not be justified.
View in article
Gaillardet, J. (2008) Isotope geochemistry as a tool for deciphering kinetics of water-rock interaction, in: Brantley, S.L., Kubicki, J.D., White, A.F. (Eds.) Kinetics of Water-Rock Interaction. Springer, New York.
 Show in context
Show in context The technique reacts a solution enriched in a rare isotope of an element with a solid having natural isotopic abundances (Beck et al., 1992; Gaillardet, 2008; Gruber et al., 2013).
View in article
Grambow, B. (1985) A general rate equation for nuclear waste glass corrosion. Materials Reserch Society Symposium Proceedings 44, 15-27.
 Show in context
Show in context Despite the scepticism expressed by experts and a growing literature describing experiments at near equilibrium that show deviations from this relationship in Equation 2 (see review by Zhu, 2009), this rate law has been widely used in scientific and technological situations, such as the performance models for high-level radioactive waste disposal (Grambow, 1985) and geological CO2 sequestration (Johnson et al., 2004; Marini, 2007).
View in article
Gruber, C., Harpaz, L., Zhu, C., Bullen, T.D., Ganor, J. (2013) A new approach for measuring dissolution rates of silicate minerals by using silicon isotopes. Geochimica et Cosmochimica Acta 104, 261-280.
 Show in context
Show in context The technique reacts a solution enriched in a rare isotope of an element with a solid having natural isotopic abundances (Beck et al., 1992; Gaillardet, 2008; Gruber et al., 2013).
View in article
Hellmann, R., Penisson, J.-M., Hervig, R.L., Thomassin, J.-H., Abrioux, M.-F. (2003) An EFTEM/HRTEM high-resolution study of the near surface of labradorite feldspar altered at acid pH: evidence for interfacial dissolution-reprecipitation. Physics and Chemistry of Minerals 30, 192-197.
 Show in context
Show in context Etch pits (Brantley et al., 1986; Lüttge, 2006) and “leached or re-precipitated layers” (Hellmann et al., 2003), which are not present at equilibrium, suggest that the extrapolation of equilibrium rate constants to highly undersaturated solutions may not be justified.
View in article
Experiments for multicomponent silicate minerals often involve changes of reaction schemes in response to departure from equilibrium (Beig and Lüttge, 2006), and a poorly understood “leached” or “re-precipitated” layer can be developed (Hellmann et al., 2003).
View in article
Johnson, J.W., Nitao, J.J., Knauss, K.G. (2004) Reactive transport modeling of CO2 storage in saline aquifers to elucidate fundamental processes, trapping mechanisms and sequestration partitioning. Geological Society of London, Special Publication 233, 107-128.
 Show in context
Show in context Despite the scepticism expressed by experts and a growing literature describing experiments at near equilibrium that show deviations from this relationship in Equation 2 (see review by Zhu, 2009), this rate law has been widely used in scientific and technological situations, such as the performance models for high-level radioactive waste disposal (Grambow, 1985) and geological CO2 sequestration (Johnson et al., 2004; Marini, 2007).
View in article
Laidler, K.J. (1987) Chemical Kinetics. Third Edition, Prentice Hall, New York.
 Show in context
Show in context Chemists have long known that “rate coefficients determined away from equilibrium are not necessarily the same as those at equilibrium, and their ratio is not necessarily equal to Kc” (Laidler, 1987, p. 287).
View in article
Lasaga, A.C. (1981) Rate laws of chemical reactions. In: Lasaga, A.C., Kirkpatrick, R.J. (Eds.) Kinetics of Geochemical Processes. Mineralogical Society of America, Washington DC, 1-68.
 Show in context
Show in context The most important and far reaching application of PDB in geology is in the so called “transition state theory rate law” or “linear rate law”, which expresses mineral dissolution rates as a function of chemical potential (or affinity) (Lasaga, 1981; Aagaard and Helgeson, 1982),
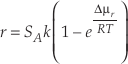
where r devotes the rate of chemical reaction, and SA the surface area. Δµr stands for the chemical potential of the reaction, R the gas constant, and T temperature in Kelvin.
View in article
Lasaga (1981) gives examples of predicting rate laws, the Arrhenius pre-exponential constants, and activation energy.
View in article
Lasaga, A.C. (1998) Kinetic Theory in the Earth Sciences. Princeton University Press, New York.
 Show in context
Show in context The principle states that at equilibrium, the rates of forward and reverse reaction rates are equal (Lasaga, 1998, p.82).
View in article
Equation 1 is a powerful link between thermodynamics and kinetics (Lasaga, 1998), and a device by which measurements of rate constants for reactions in one direction may be used to obtain the rate constants for the experimentally inaccessible reverse directions (Mahan, 1975).
View in article
Lewis, G.N. (1925) A new principle of equilibrium. Proceedings of the National Academy of Sciences of the United States of America 11, 179-183.
 Show in context
Show in context The principle of detailed balance (PDB) has been a cornerstone for irreversible thermodynamics and chemical kinetics for a long time (Wegscheider, 1901; Lewis, 1925; Onsager, 1931), and its wide application in geochemistry has mostly been implicit and without experimental testing of its applicability.
View in article
The principle of detailed balance (PDB) arose from statistical and quantum mechanics in the early twentieth century to become a foundation of modern chemical kinetics (Wegscheider, 1901; Lewis, 1925; Onsager, 1931), but its appropriate application to chemical kinetics is obscure because it is difficult to use conventional rate experiments to determine independently the forward and reverse rates at equilibrium.
View in article
Lüttge, A. (2006) Crystal dissolution kinetics and Gibbs free energy. Journal of Electron Spectroscopy and Related Phenomena 150, 248-259.
 Show in context
Show in context Etch pits (Brantley et al., 1986; Lüttge, 2006) and “leached or re-precipitated layers” (Hellmann et al., 2003), which are not present at equilibrium, suggest that the extrapolation of equilibrium rate constants to highly undersaturated solutions may not be justified.
View in article
Mahan, B.H. (1975) Microscopic reversibility and detailed balance - analysis. Journal of Chemical Education 52, 299-302.
 Show in context
Show in context Equation 1 is a powerful link between thermodynamics and kinetics (Lasaga, 1998), and a device by which measurements of rate constants for reactions in one direction may be used to obtain the rate constants for the experimentally inaccessible reverse directions (Mahan, 1975).
View in article
Marini, L. (2007) Geological Sequestration of Carbon Dioxide. Elsevier, Amsterdam.
 Show in context
Show in context Despite the scepticism expressed by experts and a growing literature describing experiments at near equilibrium that show deviations from this relationship in Equation 2 (see review by Zhu, 2009), this rate law has been widely used in scientific and technological situations, such as the performance models for high-level radioactive waste disposal (Grambow, 1985) and geological CO2 sequestration (Johnson et al., 2004; Marini, 2007).
View in article
Oelkers, E.H., Schott, J., Devidal, J.L. (1994) The effect of aluminum, pH, and chemical affinity on the rates of aluminosilicate dissolution reactions. Geochimica et Cosmochimica Acta 58, 2011-2024.
 Show in context
Show in context Aluminium may inhibit dissolution (Oelkers et al., 1994), and other non-equilibrium surface features may occur so that the far from equilibrium dissolution and precipitation reaction paths can involve different pathways.
View in article
Onsager, L. (1931) Reciprocal relations in irreversible processes. I. Physical Review 37, 405-426.
 Show in context
Show in context The principle of detailed balance (PDB) has been a cornerstone for irreversible thermodynamics and chemical kinetics for a long time (Wegscheider, 1901; Lewis, 1925; Onsager, 1931), and its wide application in geochemistry has mostly been implicit and without experimental testing of its applicability.
View in article
The principle of detailed balance (PDB) arose from statistical and quantum mechanics in the early twentieth century to become a foundation of modern chemical kinetics (Wegscheider, 1901; Lewis, 1925; Onsager, 1931), but its appropriate application to chemical kinetics is obscure because it is difficult to use conventional rate experiments to determine independently the forward and reverse rates at equilibrium.
View in article
Palandri, J.L., Kharaka, Y.K. (2004) A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling., U.S. Geological Survey Open File Report 2004-1068, 66.
 Show in context
Show in context In their widely used kinetic data compilation, Palandri and Kharaka (2004) stated that “Precipitation rate data do not exist for most minerals…”.
View in article
Rimstidt, J.D. (1997) Quartz solubility at low temperatures. Geochimica et Cosmochimica Acta 61, 2553-2558.
 Show in context
Show in context The starting solution for Type 1 experiments contained 340 mM 29SiO2, which is the solubility of quartz at 50 °C (Rimstidt, 1997), and the solution was reacted with an ion exchange resin to remove cations that would catalyse the quartz dissolution rate.
View in article
Rimstidt (1997) measured quartz solubility at 25, 50, 75, and 96 oC in experiments up to 4917 days.
View in article
These long-term experimental data formed the basis for establishing quartz solubility as a function of temperature, and also for deriving the standard thermodynamic properties for aqueous species H4SiO4(aq) (Rimstidt, 1997; Stefansson, 2001).
View in article
Applying Equation 1, we found that the log K value for reaction (3) at 50 oC in pure water is -3.50, which is within the experimental uncertainties in Rimstidt (1997).
View in article
Rimstidt, J.D. (2013) Geochemical rate models: An introduction to geochemical kinetics. Cambridge University Press.
 Show in context
Show in context We used the initial rate method (Rimstidt, 2013) to find the rate of appearance of 28Si in solution, which gives the dissolution rate at equilibrium, and the rate of disappearance of 29Si, which gives the precipitation rate at equilibrium.
View in article
Rimstidt, J.D., Barnes, H.L. (1980) The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta 44, 1683-1699.
 Show in context
Show in context Rimstidt and Barnes (1980) used this principle to obtain both k- and k+ from quartz dissolution data only.
View in article
This problem is typically circumvented by using the principle of detailed balance to recast the rate equation in terms of one rate constant and the known equilibrium constant (K = k+/k) (Rimstidt and Barnes, 1980).
View in article
Berger et al. (1994) showed that quartz dissolution rates fit Equation 5 and Rimstidt and Barnes (1980) showed that they also fit Equation 4.
View in article
Schott, J., Pokrovsky, O.S., Oelkers, E.H. (2009) The link between mineral dissolution/precipitation kinetics and solution chemistry. Reviews in Mineralogy & Geochemistry 70, 207-258.
 Show in context
Show in context This has important implications for predicting rates over a wide range of conditions as explained by Schott et al. (2009).
View in article
Stefansson, A. (2001) Dissolution of primary minerals of basalt in natural waters - I. Calculation of mineral solubilities from 0 degrees C to 350 degrees C. Chemical Geology 172, 225-250.
 Show in context
Show in context These long-term experimental data formed the basis for establishing quartz solubility as a function of temperature, and also for deriving the standard thermodynamic properties for aqueous species H4SiO4(aq) (Rimstidt, 1997; Stefansson, 2001).
View in article
Wegscheider, R. (1901) Über simultane Gleichgewichte und die Beziehungen zwischen Thermodynamik und Reactionskinetik homogener Systeme. Monatshefte für Chemie / Chemical Monthly 32, 849–906.
 Show in context
Show in context The principle of detailed balance (PDB) has been a cornerstone for irreversible thermodynamics and chemical kinetics for a long time (Wegscheider, 1901; Lewis, 1925; Onsager, 1931), and its wide application in geochemistry has mostly been implicit and without experimental testing of its applicability.
View in article
The principle of detailed balance (PDB) arose from statistical and quantum mechanics in the early twentieth century to become a foundation of modern chemical kinetics (Wegscheider, 1901; Lewis, 1925; Onsager, 1931), but its appropriate application to chemical kinetics is obscure because it is difficult to use conventional rate experiments to determine independently the forward and reverse rates at equilibrium.
View in article
Zhu, C. (2009) Geochemical modeling of reaction paths and geochemical reaction networks. Reviews in Mineralogy & Geochemistry 70, 533-569.
 Show in context
Show in context Despite the scepticism expressed by experts and a growing literature describing experiments at near equilibrium that show deviations from this relationship in Equation 2 (see review by Zhu, 2009), this rate law has been widely used in scientific and technological situations, such as the performance models for high-level radioactive waste disposal (Grambow, 1985) and geological CO2 sequestration (Johnson et al., 2004; Marini, 2007).
View in article
Zhu, C., Liu, Z., Schaefera, A., Wang, C., Zhang, G., Gruber, C., Ganor, J., Georg, R.B. (2014) Silicon isotopes as a new method of measuring silicate mineral reaction rates at ambient temperature. Procedia of Earth and Planetary Sciences 10, 189-193.
 Show in context
Show in context However, Zhu et al. (2014) showed that this method was promising to measure albite dissolution rates very close to equilibrium, and the interferences of secondary phase precipitation and isotope fractionation was negligible.
View in article
top
Supplementary Information
Supplementary Methods and Results
Derivation of the K = k+/k- and r = f(Δμr) relationships
Aagaard and Helgeson (1982) derived a rate equation that relates the time rate of change of reaction progress (ξ) to the reaction affinity (A), where reaction affinity equals negative chemical potential (Δμr)
Eq. S-1
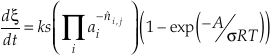
where k denotes the rate constant (mol m-2 s-1), s the surface area (m2 mol-1), R the gas constant, T temperature (K), and s the Tomkin’s average stoichiometric number. Both the chemical potential Δμr and chemical affinity A have the unit of J mol-1. This equation is sometimes called a “transition state theory rate law” even though the Aagaard and Helgeson (1982) paper makes only a passing mention of transition state theory and the derivation is actually based on the principle of detailed balance and Temkin’s average stoichiometric number (see Equations 18 and 20 in Aagaard and Helgeson, 1982).
This section shows how Equation S-1 is related to the principle of detailed balance. A key, but underappreciated, assumption in this derivation is that the reaction mechanism for the rate-determining step does not change when the reaction departs from equilibrium. As long as that assumption is true, the K = k+/k- relationship derived below, can be used in rate equations for reactions that are not at equilibrium. However, if the reaction mechanism changes when the reaction departs from equilibrium then k+/k- ≠ K (see for example p. 287 in Laidler, 1987
Laidler, K.J. (1987) Chemical Kinetics. Third Edition, Prentice Hall, New York.
) and Equation S-1 is not valid.The principle of detailed balance recognises that at equilibrium the rates of the forward and backward reactions must be equal. The consequences of this relationship are illustrated here by considering a simple reaction between two species: A and B (e.g., quartz and H4SiO4(aq)).
Eq. S-2
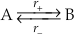
The forward reaction rate (r+) is the product of the forward rate constant (k+) and the activity of species A.
Eq. S-3
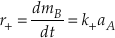
The backward reaction rate (r–) is the product of the backward rate constant (k–) and the activity of species B.
Eq. S-4
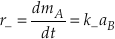
The overall reaction rate (r) is the difference between these two rates.
Eq. S-5
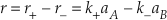
At equilibrium the forward reaction rate exactly equals the backward reaction rate so that the net rate (r) is zero. If r+ = r– then k+aA, eq = k-aB, eq and because K = aA, eq/aB, eq we find that K = k+/k-.
Eq. S-6
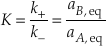
Many rate equations assume that the reaction mechanism for the rate-determining step for the equilibrium reaction remains the same at non-equilibrium conditions and that means that k+ and k- are the same at non-equilibrium conditions. This allows Equation S-5 to be written in terms of the activity ratio, Q (= aA/aB.).
Eq. S-7
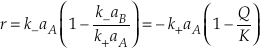
The differential rate equation for silica dissolution (Equation 33 in Rimstidt and Barnes, 1980
Rimstidt, J.D., Barnes, H.L. (1980) The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta 44, 1683-1699.
) has this form. This equation can be further transformed by expressing the chemical potential driving the reaction as a function of Q/K.Eq. S-8
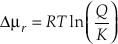
so
Eq. S-9
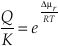
Substituting Equation S-9 into Equation S-7 gives the reaction rate as a function of the chemical potential driving the reaction.
Eq. S-10
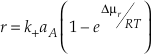
This relationship can also be written in terms of affinity (A = -µ).
Eq. S-11
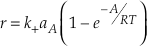
This equation is analogous to Equation 30 in Aagaard and Helgeson (1982)
Aagaard, P., Helgeson, H.C. (1982) Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. I. Theoretical considerations. American Journal of Science 282, 237-285.
except that in their equation the activity of A is raised to a power due to their incorporation of the Tempkin average stoichiometric number. That allowed them to generalise to a chain reaction rather than a single step reaction as shown here. See Boudart (1976)Boudart, M. (1976) Consistency between kinetics and thermodynamics. Journal of Physical Chemistry 80, 2869-2870.
and Hollingsworth (1957)Hollingsworth, C.A. (1957) Kinetics and equilibria of complex reactions. Journal of Chemical Physics 27, 1346-1348.
for very similar derivations.Analytical Methods
The Iota STD quartz (106–180 µm) from Unimin Corporation, New Canaan, CT, USA was used in the experiments. All of the peaks visible on the X-ray diffraction patterns were from quartz. The quartz grains were washed with deionised water to remove fine particles and then the disturbed surface layer was removed by leaching in 65° C deionised water for 4 weeks. The leaching bottle was stirred twice a day by inverting and the water was changed once a week. After 4 weeks, the quartz was recovered and washed four times with deionised water and then rinsed twice with ethyl alcohol. The quartz was air dried on aluminium foil at room temperature. The specific surface area of the quartz powder was determined using the N2 BET method (Brunauer et al., 1938
Brunauer, S., Emmett, P.H., Teller, E. (1938) Adsorption of gases in multimolecular layers. Journal of the American Chemical Society 60, 309-319.
).The NaOH fusion method was used to prepare the 29SiO2 solution. We mixed 0.0488 ± 0.001 g of 29SiO2 powder (0.04 % 28Si, 99.90 % 29Si, and 0.06 % 30Si from Isoflex, San Francisco, CA, USA) and 0.3200 ± 0.001 g of NaOH in a silver crucible and then fired the crucible at 730 °C in a muffle furnace for 10 min. After slight cooling, the crucible contents were dissolved into 30 mL deionised water and washed with 470 mL deionised water into a Teflon bottle. This solution was diluted to produce a solution with 97.6 ppm 29SiO2. Sodium was removed from this solution using a Bio-Rad cation exchange resin AG 50W-X8 (100-200 mesh) in H+ form distributed as a 1.8 mL resin bed in each of seven Bio-Rad columns. The resin was prepared by rinsing it with 50 mL of 1 M HCl. Before loading the sample on the resin, the pH was adjusted to near 5.5 to ensure complete removal of any acids. Each column treated 31 mL of the 97.6 ppm 29SiO2 solution. Then an additional 4 mL of deionised water was passed through each column. The effluent solution was diluted to 1 L so that the final cation free solution with a pH of 5.28 had a 29SiO2 concentration of 21 ppm.
Each experiment consisted of 10 leak-proof 30 mL polypropylene bottles each containing 30 g of quartz grains and either 15 mL of the 21 ppm 29SiO2 solution or deionised water. The bottles were stirred twice per day by inverting. Five replicates of each experiment type were run. At the predetermined sampling time, a bottle was opened and the solution was recovered using a vacuum filter system (0.45 µm nitrocellulose sterile analytical filter). Part of the solution was used for a pH measurement and the remainder was stored in a refrigerator at 4.0 °C until analysis. The silica concentration of the solution samples was measured using the molybdate blue method (Govett, 1961
Govett, G.J.S. (1961) Critical factors in the colorimetric determination of silica. Analytica Chimica Acta 25, 69-80.
). The precision of this method in our laboratory is about ±4 %.The Si isotope abundances were measured using high-resolution multiple-collector inductively coupled plasma mass spectrometry (HR-MC-ICP-MS, Nu Plasma II, Wrexham, UK) at Northwest University, China. Blank samples were filled with ultrapure deionised water, and acidified with ultrapure HNO3. The 28Si, 29Si and 30Si abundances were measured using Faraday cups under static mode. Instrumental sensitivity was ~11V/ μg g-1 for 28Si in high-resolution mode. Sample solution was introduced into MC-ICP-MS using a dry aerosol system (Aridus II, Cetac, USA) and a 100 μL min-1 PFA micro-flow nebuliser. We used standard bracketing method (Alfa Aesar Si, Stock# 38717, LOT 591543G) to calculate δ29Si and δ30Si and every sample was measured three times using the Time-Resolved-Analysis (TRA) method. The relative standard deviation (RSD) of the three ratios was used to evaluate the data quality. Only those analyses with RSDs (δ30Si) < 10 % were reported and samples with RSDs (δ30Si) > 10 % were re-measured.
Supplementary Information References
Aagaard, P., Helgeson, H.C. (1982) Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. I. Theoretical considerations. American Journal of Science 282, 237-285.
 Show in context
Show in context This equation is analogous to Equation 30 in Aagaard and Helgeson (1982) except that in their equation the activity of A is raised to a power due to their incorporation of the Tempkin average stoichiometric number.
View in Supplementary Information
Boudart, M. (1976) Consistency between kinetics and thermodynamics. Journal of Physical Chemistry 80, 2869-2870.
 Show in context
Show in context See Boudart (1976) and Hollingsworth (1957) for very similar derivations.
View in Supplementary Information
Brunauer, S., Emmett, P.H., Teller, E. (1938) Adsorption of gases in multimolecular layers. Journal of the American Chemical Society 60, 309-319.
 Show in context
Show in context The specific surface area of the quartz powder was determined using the N2 BET method (Brunauer et al., 1938).
View in Supplementary Information
Govett, G.J.S. (1961) Critical factors in the colorimetric determination of silica. Analytica Chimica Acta 25, 69-80.
 Show in context
Show in contextThe silica concentration of the solution samples was measured using the molybdate blue method (Govett, 1961).
View in Supplementary Information
Hollingsworth, C.A. (1957) Kinetics and equilibria of complex reactions. Journal of Chemical Physics 27, 1346-1348.
 Show in context
Show in context See Boudart (1976) and Hollingsworth (1957) for very similar derivations.
View in Supplementary Information
Laidler, K.J. (1987) Chemical Kinetics. Third Edition, Prentice Hall, New York.
 Show in context
Show in context However, if the reaction mechanism changes when the reaction departs from equilibrium then k+/k- ≠ K (see for example p. 287 in Laidler, 1987) and Equation S-1 is not valid.
View in Supplementary Information
Rimstidt, J.D., Barnes, H.L. (1980) The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta 44, 1683-1699.
 Show in context
Show in contextThe differential rate equation for silica dissolution (Equation 33 in Rimstidt and Barnes, 1980) has this form.
View in Supplementary Information