Reorganisation of Earth's biogeochemical cycles briefly oxygenated the oceans 520 Myr ago
Affiliations | Corresponding Author | Cite as | Funding information- Share this article





-
Article views:12,409Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract
Figures and Tables
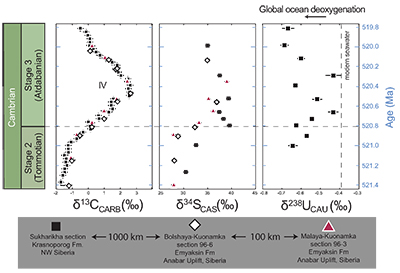 Figure 1 Isotope data from three carbonate successions straddling the Cambrian Stage 2–3 boundary (Cambrian Stage 2–3) in Siberia. Carbon isotope data from carbonate (δ13CCARB) is taken from Kouchinsky et al. (2007). Sulphur and uranium isotope data are from carbonate-associated sulphate (δ34SCAS) and uranium (δ238UCAU), respectively. Age assignments derived from correlations to the carbon isotope stratigraphy and the age model of Maloof et al. (2010). | 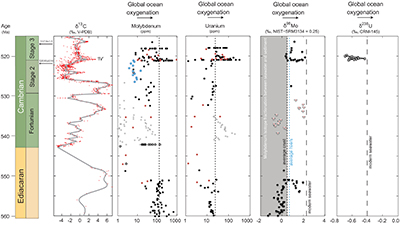 Figure 2 Summary of the redox proxy and carbon isotope data from latest Ediacaran to Early Cambrian (560–515 Myr). Redox proxy data includes the sedimentary contents and stable isotope compositions of molybdenum and uranium: Euxinic shales (black circles), Ferruginous shales (red circles), oxic shales (blue circles), shales from unknown redox environments (gray crosses), phosphorites (white diamonds), and carbonates (white circles). The grey field on the molybdenum isotope plot indicates values that are definitively fractionated from seawater, although values greater than these may be so as well. References for the data are listed in the Supplementary Information Extended Data, Table S-22. |  Figure 3 Conceptual model for the episodic expansion of the oxygenation zone in the oceans. The emergence of bilaterian animals (a-b) increased sediment mixing via bioturbation causing atmospheric pO2 to decline. The oxygenation zone contracts until (c) a rapid increase in the sinking rate of organic matter changes O2 consumption rates in the upper water column. (d) This accelerates organic carbon export to the sediments and delivers more food and O2 to the benthos over wider areas of the seafloor. Enhanced bioturbation promotes atmospheric pO2 decline, and re-stabilises the ocean in a more reducing state. Arrows and numbers illustrate organic export fluxes in one scenario (details in Table S-11). For simplicity, the organic C export increases in one step with the emergence of larger faecal pellets. Quantitative estimates for organic carbon export and remineralisation are derived from the coupled C and S isotope modelling (see Supplementary Information S5). |
| Figure 1 | Figure 2 | Figure 3 |
Supplementary Figures and Tables
 Figure S-1 Location of the studied sections Sukharikha (S), Bolshaya Kuonamka (6) and Malaya Kuonamka (3) and other sections at the Siberian platform discussed in the text (L–Middle Lena, A–Aldan Rivers). | 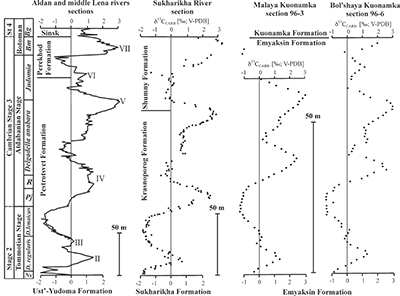 Figure S-2 Carbon isotope stratigraphy of the three studied sections and composite curve from Aldan and Middle Lena Rivers (Brasier et al., 1994; Kouchinsky et al., 2007). Zones as defined in the Lena-Aldan area: Ns – Nochoroicyathus sunnaginicus; D. regularis – Dokidocyathus regularis; D. lenaicus – Dokidocyathus lenaicus–Tumuliolynthus primigenius; Pj – Profallotaspis jakutensis; R – Repinaella; Bm – Bergeroniellus micmacciformis; Bg – Bergeroniellus gurarii. | 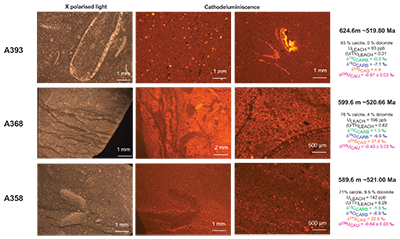 Figure S-3 Photomicrographs of samples (A358, A368 and A393) from the Sukharikha River section show microstructure and cathodoluminescent (CL) characteristics. Recrystallised shell fragments are embedded in a micrite matrix. Photographs are taken from thin section using multi-composite exposure (HDR). Selected geochemical data are summarised; n.d. – no data. | 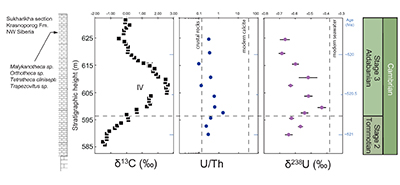 Figure S-4 Geochemical profiles from the Sukharikha River section showing δ13C, U/Th (note the logarithmic scale) and δ238U in stratigraphic context. The lithostratigraphy is adapted from Kouchinsky et al. (2007) and Rowland et al. (1998). The age assignment follows the model proposed by Maloof et al. (2010) assuming synchronicity worldwide in δ13C record tied to five absolute U/Pb age dates obtained from interbedded volcanic ashes in sections from Morocco (Maloof et al., 2010a). The uncertainty on δ13C is smaller than symbol size (2 SD reproducibility of samples from the same bed). The uncertainty of U/Th is <30 % measured on replicate leachates (see Extended Data 1). The uncertainty of δ238U is shown with error bars as 2 SE (replicate analyses of the same sample solution, see Table S-1). |  Figure S-5 Comparison of δ238U and highly reactive U to δ13C and geochemical indicators of dolomitisation (Mg/Ca, dolomite), pore water redox conditions (TOC), diagenetic alteration (Mn/Sr, δ18O), detrital input (Al/Ca, clay content), and primary carbonate mineralogy (Sr/Ca). |
| Figure S-1 | Figure S-2 | Figure S-3 | Figure S-4 | Figure S-5 |
 Table S-1 Pearson's correlation coefficients and p-values calculated to test the influence of diagenetic indicators on δ238U and U/Th. Uranium content (U) is linearly correlated to U/Th, hence the significance of the correlations between U and diagenetic indicators are similar. Statistical significant relationships are in bold (confidence interval = 5 %). |  Table S-2 Uranium extracted from two reference materials with the sequential extraction procedure. |  Table S-3 Comparison of extraction yields for acetic acid vs. hydrochloric acid of various molarity. |  Table S-4 Repeated analyses of carbonate-associated U and δ238UCAU using the mild acetic acid extraction (with variable reaction time). |  Table S-5 Extraction yields for various mixtures of KTChalk and MCPhos. |  Table S-6 Five parameterisations for the modern oceanic uranium isotope budget shown in Figure S-6. The models are broadly consistent with the modern ocean state. | 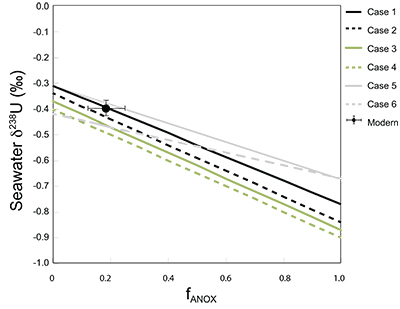 Figure S-6 Relationships between δSW and anoxic U burial fraction (fU) in the ocean are shown when the system is at steady state. The fraction of total oceanic U burial in anoxic basins (fU) is a key parameter that can shift seawater δ238U significantly below the modern value (black circle). The remaining U burial occurs in various oxygenated settings with a smaller isotopic imprint on global seawater (see text for details). |  Table S-7 Parameter values used in the coupled Mo–U isotope mass balance models for today's ocean. |
| Table S-1 | Table S-2 | Table S-3 | Table S-4 | Table S-5 | Table S-6 | Figure S-6 | Table S-7 |
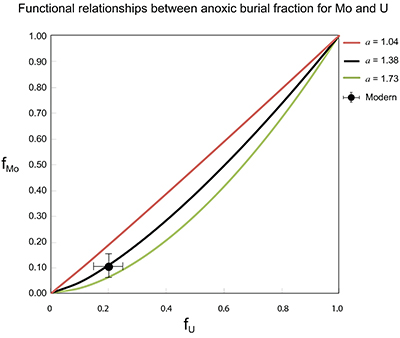 Figure S-7 Modelled functional relationships between euxinic Mo and U sinks. Modern estimates for the anoxic burial fractions (white square) suggest a is slightly larger than 1, consistent with modern oceanic budgets (Noordmann et al., 2016) where a = 1.38 ± 0.34. | 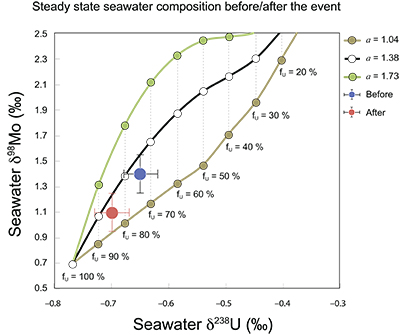 Figure S-8 Modelled seawater composition (δ238U, δ98Mo) for the early Cambrian steady states before and after the Cambrian Stage 2–3 event. The left most point represents 100 % burial in anoxic settings (fU = fMo = 1). At each step point towards the right, fU decreases 10 % (i.e. 90 %, 80 %, 70 %, etc.). The estimated composition of the δ238U and δ98Mo of early Cambrian seawater in ‰ before and after the event are (-0.65, -0.70) and (1.4, 1.1), respectively, Error bars show ±0.03 ‰ and ±0.15 for δ238U and δ98Mo, respectively. | 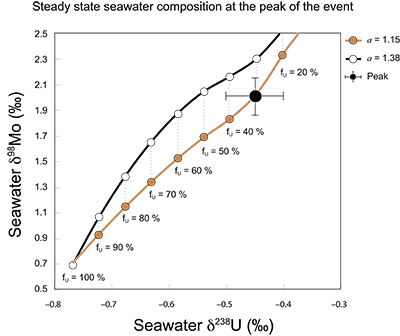 Figure S-9 The predicted composition of seawater at steady state for a = 1.15–1.38 is consistent with observations at the peak of the oxygenation event (δ238U = –0.45 ‰, δ98Mo = 2.0 ‰) with only 30 ± 10 % U removal into anoxic settings (corresponding to 25 ± 10 % and 19 ± 8 % Mo removal for a = 1.15 and 1.38, respectively). |  Table S-8 Parameter values used for the C and S modelling. |  Table S-9 Changes in the f-ratios during the Cambrian Stage 2–3 oxygenation episode. Uncertainties are propagated from the uncertainty of the isotope compositions of the inputs and the isotope fractionation associated with burial in reducing sinks (Table S-8) |  Table S-10 Ratios between reducing and oxidising sinks for carbon and sulphur changed during the Cambrian Stage 2–3 event. |  Table S-10 Consequences for absolute organic carbon and pyrite sulphur flux, assuming modern-day values for JCARB, JEVAP, and α. The other constants are δIN, C = –5 ‰, δIN, S = 8 ‰, ΔS = 35 ‰, ΔBIO = 26 ‰. Flux unit: mol/yr. |  Table S-12 Calculations with α = 0.070 (= 10 x modern). The higher α value leads to a solution with more modest organic load fluxes and less remineralisation, fREMIN < 0.76. |
| Figure S-7 | Figure S-8 | Figure S-9 | Table S-8 | Table S-9 | Table S-10 | Table S-11 | Table S-12 |
 Table S-13 Calculations with oxidative burial fluxes (JCARB, JEVAP) set at 1/4 of modern values. α set at 0.070. |  Table S-14 Calculations with ΔS set at 50 ‰ (as opposed to 35 ‰). α = 0.070. |  Table S-15 Calculations with δIN,S set at 16 ‰ (as opposed to 8 ‰). α = 0.070. |  Table S-16 Calculations with δIN,C set at –4 ‰ (as opposed to –5 ‰). α = 0.070. |  Table S-17 Calculations with ΔBIO = 30 ‰ (as opposed to 26 ‰). α = 0.070. |  Table S-18 Summary of selected solutions and the increasing organic rain rate during the Cambrian Stage 2–3 event. | 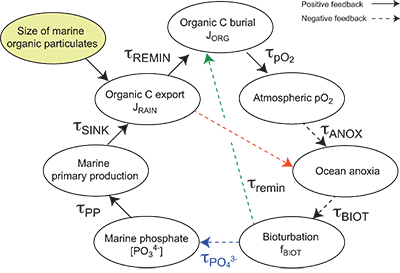 Figure S-10 Feedback diagram showing the oxygenation dynamics of the atmosphere-ocean system in response to increasing sinking rates of particulate organic matter in the oceans by larger animals with guts. See text for details. |
| Table S-13 | Table S-14 | Table S-15 | Table S-16 | Table S-17 | Table S-18 | Figure S-10 |
 Table S-19 Elemental and isotope data for samples from the Sukharikha River Section. Reference materials include IAPSO seawater, argillaceous limestone (SRM-1d), carbonatite (COQ-1) and Columbia River basalt (BCR-2). rpt = repeated analyses. |  Table S-20 Mineralogical data for samples from the Sukharikha River section. |  Table S-21 Sulphur isotope data of carbonate associated sulphate and total organic carbon content in samples from three Siberian sections (Sukharika River (A), Bolshaya Kuonamka river (K3), and Malaya Kuonamka river (K6)). Published C and O isotope data are shown for comparison (Kouchinsky et al., 2007). |  Table S-22 Data sources for the marine redox proxy data (Mo, U, δ98Mo and δ238U) from Late Ediacaran and Cambrian sedimentary archives (modified after Boyle et al., 2014). All Mo isotope data were corrected from in-house reference materials to the NIST SRM 3136 scale (Goldberg et al., 2013; Nägler et al., 2014). |
| Table S-19 | Table S-20 | Table S-21 | Table S-22 |
top
Letter
In contrast to many geochemical proxies that evaluate local ancient marine redox including iron speciation and trace metal (Mo, U, V) enrichments, the uranium isotope composition (δ238U, the per mille deviation of the 238U/235U ratio relative to CRM 145 standard) of seawater can be used to evaluate ocean oxygenation at a globally integrated scale. This is possible due to the long residence time and uniform δ238U of uranium in the modern ocean and predicted for the Cambrian ocean (Weyer et al., 2008
Weyer, S., Anbar, A.D., Gerdes, A., Gordon, G.W., Algeo, T.J., Boyle, E.A. (2008) Natural fractionation of 238U/235U. Geochimica et Cosmochimica Acta 72, 345–359.
; Dahl et al., 2014Dahl, T.W., Boyle, R.A., Canfield, D.E., Connelly, J.N., Gill, B.C., Lenton, T.M., Bizzarro, M. (2014) Uranium isotopes distinguish two geochemically distinct stages during the later Cambrian SPICE event. Earth and Planetary Science Letters 401, 313–326.
; Tissot and Dauphas, 2015Tissot, F.L.H., Dauphas, N. (2015) Uranium isotopic compositions of the crust and ocean: Age corrections, U budget and global extent of modern anoxia. Geochimica et Cosmochimica Acta 167, 113–143.
). The δ238U proxy has been utilised to track past global ocean redox during three known oceanic anoxic events (Montoya-Pino et al., 2010Montoya-Pino, C., Weyer, S., Anbar, A.D., Pross, J., Oschmann, W., van de Schootbrugge, B., Arz, H.W. (2010) Global enhancement of ocean anoxia during Oceanic Anoxic Event 2: A quantitative approach using U isotopes. Geology 38, 315–318.
; Brennecka et al., 2011Brennecka, G.A., Herrmann, A.D., Algeo, T.J., Anbar, A.D. (2011) Rapid expansion of oceanic anoxia immediately before the end-Permian mass extinction. Proceedings of the National Academy of Sciences 108, 17631–17634.
; Dahl et al., 2014Dahl, T.W., Boyle, R.A., Canfield, D.E., Connelly, J.N., Gill, B.C., Lenton, T.M., Bizzarro, M. (2014) Uranium isotopes distinguish two geochemically distinct stages during the later Cambrian SPICE event. Earth and Planetary Science Letters 401, 313–326.
; Elrick et al., 2016Elrick, M., Polyak, V., Algeo, T.J., Romaniello, S., Asmerom, Y., Herrmann, A.D., Anbar, A.D., Zhao, L., Chen, Z.-Q. (2016) Global-ocean redox variation during the middle-late Permian through Early Triassic based on uranium isotope and Th/U trends of marine carbonates. Geology, G38585.1.
; Lau et al., 2016Lau, K.V., Maher, K., Altiner, D., Kelley, B.M., Kump, L.R., Lehrmann, D.J., Silva-Tamayo, J.C., Weaver, K.L., Yu, M., Payne, J.L. (2016) Marine anoxia and delayed Earth system recovery after the end-Permian extinction. Proceedings of the National Academy of Science USA 113, 2360–2365.
), where anoxic water masses expanded over larger areas of the seafloor and caused negative δ238U excursions. Here, we use uranium isotopes to identify a transient global oxygenation episode during the radiation of animals in the Cambrian.Our new δ238U data of carbonate-associated uranium comes from limestones collected from the Siberian Platform across the provisional Cambrian Stage 2–3 boundary (~521 to 520 million years ago) (Fig. 1), when animals that shed their exoskeleton (ecdysozoa) began to diversify (Maloof et al., 2010
Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
; Kouchinsky et al., 2012Kouchinsky, A., Bengtson, S., Runnegar, B., Skovsted, C., Steiner, M., Vendrasco, M. (2012) Chronology of early Cambrian biomineralization. Geological Magazine 149, 221–251.
). A perturbation in the marine carbon cycle is expressed at this time as a large positive carbon isotope excursion recognised globally and in all studied sections; geological maps and stratigraphic sections are shown in Figures S-1 and S-2 (Maloof et al., 2010Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
). This excursion serves as an important stratigraphic marker, although little is known about the biogeochemical significance of the event. The end-Stage 2 samples carry low δ238U values of –0.65 ‰, increasing stratigraphically to a value of –0.45 ‰ that approaches the modern oxygenated oceans, –0.39 ± 0.01 ‰ (Tissot and Dauphas, 2015Tissot, F.L.H., Dauphas, N. (2015) Uranium isotopic compositions of the crust and ocean: Age corrections, U budget and global extent of modern anoxia. Geochimica et Cosmochimica Acta 167, 113–143.
), before again returning in two steps to –0.7 ‰. This positive δ238U excursion of +0.25 ‰ coincides with the positive carbon isotope excursion, suggesting that they are both linked to the changes in global seawater chemistry. The samples display no systematic correlation between the δ238U excursion and indicators of dolomitisation (Mg/Ca, dolomite), pore water redox conditions (total organic carbon content), diagenetic alteration (Mn/Sr, δ18O) detrital input (Al/Ca, clay content) and primary carbonate mineralogy (Sr/Ca; see Supplementary Information S2) that might produce such a positive δ238U excursion, offset from contemporaneous seawater. That said, our samples consist of (abiotic) micrite with (biotic) shells made of secondary calcite (Fig. S-3). The difference between abiotic and biotic precipitation of calcite δ238U is predicted to induce a ~0.1 ‰ offset from seawater (Chen et al., 2016Chen, X., Romaniello, S.J., Herrmann, A.D., Wasylenki, L.E., Anbar, A.D. (2016) Uranium isotope fractionation during coprecipitation with aragonite and calcite. Geochimica et Cosmochimica Acta 188, 189–207.
). As we cannot determine the ratio of U derived from abiotic to biotic sources, we conclude that at this level of confidence, an overall positive δ238U trend is observed in the stratigraphy that we ascribe to secular changes of open marine δ238U in early Cambrian seawater. We note that our data set is limited to only one section and predict the same trend can be observed in other marine deposits with authigenic U enrichments.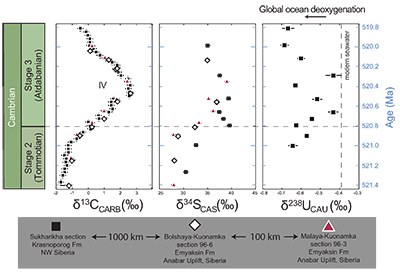
Figure 1 Isotope data from three carbonate successions straddling the Cambrian Stage 2–3 boundary (Cambrian Stage 2–3) in Siberia. Carbon isotope data from carbonate (δ13CCARB) is taken from Kouchinsky et al. (2007)
Kouchinsky, A., Bengtson, S., Pavlov, V., Runnegar, B., Torssander, P., Young, E., Ziegler, K. (2007) Carbon isotope stratigraphy of the Precambrian–Cambrian Sukharikha River section, northwestern Siberian platform. Geological Magazine 144, 1–10.
. Sulphur and uranium isotope data are from carbonate-associated sulphate (δ34SCAS) and uranium (δ238UCAU), respectively. Age assignments derived from correlations to the carbon isotope stratigraphy and the age model of Maloof et al. (2010)Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
.The positive excursion of seawater δ238U represents a global oxygenation period in the oceans that dramatically decreased the fraction (fU) of total U burial occurring in anoxic marine settings. A simple isotope mass balance calculation constrains fU from the δ238U of seawater (δSW) (see derivation in Supplementary Information S4). This calculation assumes an isotopically constant U input from rivers and a constant isotope fractionation between seawater and the U sinks. The modern ocean is at steady state with δ238U at –0.39 ± 0.01 ‰ and estimates for the average oceanic input range from –0.30 ‰ to –0.27 ‰ (Tissot and Dauphas, 2015
Tissot, F.L.H., Dauphas, N. (2015) Uranium isotopic compositions of the crust and ocean: Age corrections, U budget and global extent of modern anoxia. Geochimica et Cosmochimica Acta 167, 113–143.
; Noordmann et al., 2016Noordmann, J., Weyer, S., Georg, R.B., Jons, S., Sharma, M. (2016) 238U/235U isotope ratios of crustal material, rivers and products of hydrothermal alteration: new insights on the oceanic U isotope mass balance. Isotopes in Environmental Health Studies 52, 141–163.
). If the anoxic proportion of global U burial (fU) today is 12–25 % (Morford and Emerson, 1999Morford, J.L., Emerson, S. (1999) The geochemistry of redox sensitive trace metals in sediments. Geochimica Et Cosmochimica Acta 63, 1735–1750.
; Dunk et al., 2002Dunk, R.M., Mills, R.A., Jenkins, W.J. (2002) A reevaluation of the oceanic uranium budget for the Holocene. Chemical Geology 190, 45–67.
; Noordmann et al., 2016Noordmann, J., Weyer, S., Georg, R.B., Jons, S., Sharma, M. (2016) 238U/235U isotope ratios of crustal material, rivers and products of hydrothermal alteration: new insights on the oceanic U isotope mass balance. Isotopes in Environmental Health Studies 52, 141–163.
), and anoxic settings impart a +0.5 ± 0.1 ‰ net isotope offset from overlying seawater, this implies that the average isotope fractionation between seawater and all other oxic U sinks (ΔOTHER) is –0.02 ± 0.05 ‰. Given this formulation, we calculate that 68 ± 18 % of marine U burial before the Stage 2–3 event occurred in anoxic parts of the oceans when δ238U of seawater was –0.65 ‰. This scenario compares to the ocean state during the anoxic expansion associated with the end-Permian extinction (Brennecka et al., 2011Brennecka, G.A., Herrmann, A.D., Algeo, T.J., Anbar, A.D. (2011) Rapid expansion of oceanic anoxia immediately before the end-Permian mass extinction. Proceedings of the National Academy of Sciences 108, 17631–17634.
). Further, the anoxic U burial fraction declined to 29 ± 12 % at the peak of the event and then afterward returned to a more reducing ocean state with 78 ± 20 % anoxic U burial (Fig. S-2). The stated uncertainties for fU in the Cambrian are propagated errors from ΔOTHER, ΔANOX, and δIN reflecting a range of plausible parameterisations of the marine U cycle (see sensitivity analysis in Supplementary Information S4 for details). These data consistently require the Cambrian Stage 2–3 event to have occurred when the oceans were far more reducing than today, culminating at an oxygenation state similar to the modern ocean.Existing palaeoredox studies also point to ocean oxygenation during the Early Cambrian (Fig. 2). Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008
Wille, M., Nagler, T.F., Lehmann, B., Schroder, S., Kramers, J.D. (2008) Hydrogen sulphide release to surface waters at the Precambrian/Cambrian boundary. Nature 453, 767–769.
; Wen et al., 2011Wen, H., Carignan, J., Zhang, Y., Fan, H., Cloquet, C., Liu, S. (2011) Molybdenum isotopic records across the Precambrian-Cambrian boundary. Geology 39, 775–778.
; Xu et al., 2012Xu, L., Lehmann, B., Mao, J., Nägler, T.F., Neubert, N., Böttcher, M.E., Escher, P. (2012) Mo isotope and trace element patterns of Lower Cambrian black shales in South China: Multi-proxy constraints on the paleoenvironment. Chemical Geology 318-319, 45–59.
; Chen et al., 2015Chen, X., Ling, H.F., Vance, D., Shields-Zhou, G.A., Zhu, M., Poulton, S.W., Och, L.M., Jiang, S.Y., Li, D., Cremonese, L., Archer, C. (2015) Rise to modern levels of ocean oxygenation coincided with the Cambrian radiation of animals. Nature Communications 6, 7142.
; Kendall et al., 2015Kendall, B., Komiya, T., Lyons, T.W., Bates, S.M., Gordon, G.W., Romaniello, S.J., Jiang, G., Creaser, R.A., Xiao, S., McFadden, K., Sawaki, Y., Tahata, M., Shu, D., Han, J., Li, Y., Chu, X., Anbar, A.D. (2015) Uranium and molybdenum isotope evidence for an episode of widespread ocean oxygenation during the late Ediacaran Period. Geochimica et Cosmochimica Acta 156, 173–193.
; Wen et al., 2015Wen, H., Fan, H., Zhang, Y., Cloquet, C., Carignan, J. (2015) Reconstruction of early Cambrian ocean chemistry from Mo isotopes. Geochimica et Cosmochimica Acta 164, 1–16.
). The last positive δ98Mo excursion is broadly correlated to the first appearance of trilobites in China, strong Mo enrichments and with the oxygenation event reported here (Dahl et al., 2010Dahl, T.W., Hammarlund, E.U., Anbar, A.D., Bond, D.P.G., Gill, B.C., Gordon, G.W., Knoll, A.H., Nielsen, A.T., Schovsbo, N.H., Canfield, D.E. (2010) Devonian rise in atmospheric oxygen correlated to the radiations of terrestrial plants and large predatory fish. Proceedings of the National Academy of Sciences 107, 17911–17915.
; Xu et al., 2012Xu, L., Lehmann, B., Mao, J., Nägler, T.F., Neubert, N., Böttcher, M.E., Escher, P. (2012) Mo isotope and trace element patterns of Lower Cambrian black shales in South China: Multi-proxy constraints on the paleoenvironment. Chemical Geology 318-319, 45–59.
; Chen et al., 2015Chen, X., Ling, H.F., Vance, D., Shields-Zhou, G.A., Zhu, M., Poulton, S.W., Och, L.M., Jiang, S.Y., Li, D., Cremonese, L., Archer, C. (2015) Rise to modern levels of ocean oxygenation coincided with the Cambrian radiation of animals. Nature Communications 6, 7142.
; Wen et al., 2015Wen, H., Fan, H., Zhang, Y., Cloquet, C., Carignan, J. (2015) Reconstruction of early Cambrian ocean chemistry from Mo isotopes. Geochimica et Cosmochimica Acta 164, 1–16.
; Jin et al., 2016Jin, C., Li, C., Algeo, T.J., Planavsky, N.J., Cui, H., Yang, X., Zhao, Y., Zhang, X., Xie, S. (2016) A highly redox-heterogeneous ocean in South China during the early Cambrian (∼529–514 Ma): Implications for biota-environment co-evolution. Earth and Planetary Science Letters 441, 38–51.
). The coincident positive δ98Mo and δ238U excursions point to a widespread oxygenation episode in the earliest Cambrian Stage 3 oceans where O2-rich waters expanded and affected the Mo and U isotope composition of seawater as the overall burial fluxes of Mo and U into anoxic and euxinic settings decreased. We can predict the δ98Mo trajectory of seawater from the oceanic δ238U trajectory, if we assume the anoxic burial proportions of total Mo and U burial (fMo, fU) are correlated. We adopt a power law relationship fMo = fUα that satisfies fMo = fU = 1 during extreme anoxia and fMo = fU = 0 for extreme oxia. Using the modern ocean state as a calibration point, we find that α = 1.34 ± 0.38 (see Supplementary Information for details). Based on this relationship, average seawater δ98Mo should have increased from 1.40 ‰ in the Cambrian Stage 2 to a peak at 2.0 ‰ before returning to 1.10 ‰ during the δ238U excursion. This prediction is in good agreement with the maximum values observed in the δ98Mo record during this time interval (Lehmann et al., 2007Lehmann, B., Nägler, T.F., Holland, H.D., Wille, M., Mao, J., Pan, J., Ma, D., Dulski, P. (2007) Highly metalliferous carbonaceous shale and Early Cambrian seawater. Geology 35, 403.
; Chen et al., 2015Chen, X., Ling, H.F., Vance, D., Shields-Zhou, G.A., Zhu, M., Poulton, S.W., Och, L.M., Jiang, S.Y., Li, D., Cremonese, L., Archer, C. (2015) Rise to modern levels of ocean oxygenation coincided with the Cambrian radiation of animals. Nature Communications 6, 7142.
; Wen et al., 2015Wen, H., Fan, H., Zhang, Y., Cloquet, C., Carignan, J. (2015) Reconstruction of early Cambrian ocean chemistry from Mo isotopes. Geochimica et Cosmochimica Acta 164, 1–16.
) (Fig. 2). Collectively, the Mo and U isotopes indicate a transient, rather than a persistent change in ocean oxygenation at the beginning of Stage 3. This implies that earlier positive δ98Mo excursions (~2 ‰) in Terreneuvian phosphorite deposits (Wen et al., 2011Wen, H., Carignan, J., Zhang, Y., Fan, H., Cloquet, C., Liu, S. (2011) Molybdenum isotopic records across the Precambrian-Cambrian boundary. Geology 39, 775–778.
), and perhaps in the latest Ediacaran (Kendall et al., 2015Kendall, B., Komiya, T., Lyons, T.W., Bates, S.M., Gordon, G.W., Romaniello, S.J., Jiang, G., Creaser, R.A., Xiao, S., McFadden, K., Sawaki, Y., Tahata, M., Shu, D., Han, J., Li, Y., Chu, X., Anbar, A.D. (2015) Uranium and molybdenum isotope evidence for an episode of widespread ocean oxygenation during the late Ediacaran Period. Geochimica et Cosmochimica Acta 156, 173–193.
), represent episodic events rather than persistent ocean oxygenation. Similarly, detailed studies of the bottom water redox conditions in the Nanhua Basin, South China, suggest that oxygenated waters also invaded shallower part of the basin later in the Stage 3 (Jin et al., 2016Jin, C., Li, C., Algeo, T.J., Planavsky, N.J., Cui, H., Yang, X., Zhao, Y., Zhang, X., Xie, S. (2016) A highly redox-heterogeneous ocean in South China during the early Cambrian (∼529–514 Ma): Implications for biota-environment co-evolution. Earth and Planetary Science Letters 441, 38–51.
). As such, the oxygenation history of the early Cambrian ocean appears more dynamic than previously thought (e.g., Dahl et al., 2010Dahl, T.W., Hammarlund, E.U., Anbar, A.D., Bond, D.P.G., Gill, B.C., Gordon, G.W., Knoll, A.H., Nielsen, A.T., Schovsbo, N.H., Canfield, D.E. (2010) Devonian rise in atmospheric oxygen correlated to the radiations of terrestrial plants and large predatory fish. Proceedings of the National Academy of Sciences 107, 17911–17915.
; Sperling et al., 2013Sperling, E.A., Frieder, C.A., Raman, A.V., Girguis, P.R., Levin, L.A., Knoll, A.H. (2013) Oxygen, ecology, and the Cambrian radiation of animals. Proceedings of the National Academy of Sciences 110, 13446–13451.
; Chen et al., 2015Chen, X., Ling, H.F., Vance, D., Shields-Zhou, G.A., Zhu, M., Poulton, S.W., Och, L.M., Jiang, S.Y., Li, D., Cremonese, L., Archer, C. (2015) Rise to modern levels of ocean oxygenation coincided with the Cambrian radiation of animals. Nature Communications 6, 7142.
).
Figure 2 Summary of the redox proxy and carbon isotope data from latest Ediacaran to Early Cambrian (560–515 Myr). Redox proxy data includes the sedimentary contents and stable isotope compositions of molybdenum and uranium: Euxinic shales (black circles), Ferruginous shales (red circles), oxic shales (blue circles), shales from unknown redox environments (gray crosses), phosphorites (white diamonds), and carbonates (white circles). The grey field on the molybdenum isotope plot indicates values that are definitively fractionated from seawater, although values greater than these may be so as well. References for the data are listed in the Supplementary Information Extended Data, Table S-22.
The oxygenation event coincides with global changes in the marine carbon and sulphur cycles. We also report sulphur isotope data from carbonate-associated sulphate (δ34SCAS) from three distinct stratigraphic sections in Siberia that show a similar systematic positive δ34SCAS isotope excursion coinciding with the δ238U and δ13C excursions (Fig. 1). The simultaneous excursions across the Cambrian Stage 2-3 boundary suggest the C, S and U cycles responded to the same global biogeochemical event. Similar parallel positive carbon and sulphur isotope excursions during the late Cambrian SPICE event (Gill et al., 2011
Gill, B.C., Lyons, T.W., Young, S.A., Kump, L.R., Knoll, A.H., Saltzman, M.R. (2011) Geochemical evidence for widespread euxinia in the later Cambrian ocean. Nature 469, 80–83.
; Dahl et al., 2014Dahl, T.W., Boyle, R.A., Canfield, D.E., Connelly, J.N., Gill, B.C., Lenton, T.M., Bizzarro, M. (2014) Uranium isotopes distinguish two geochemically distinct stages during the later Cambrian SPICE event. Earth and Planetary Science Letters 401, 313–326.
) and the Botoman Sinsk event were interpreted to represent a period of enhanced organic carbon and pyrite burial (Zhuravlev and Wood, 1996Zhuravlev, A., Wood, R. (1996) Anoxia as the cause of the mid-Early Cambrian (Botomian) extinction event. Geology 24, 311–314.
). While these events are linked to expanding ocean anoxia and animal extinctions, the positive δ238U excursion reported here reveals a distinct driver for the environmental change.The Cambrian Stage 2–3 event coincides with the onset of the first major diversification of arthropods, which predates by a few million years the first appearance of macrozooplankton and suspension-feeding anomalocarids (Hou, 2004
Hou, X.G., Aldridge, R.J., Bergström, J., Siveter, D.J., Siveter, D.J., Feng, X.H. (2004) The Cambrian fossils of Chengjiang, China - the flowering of early animal life. Blackwell Publishing, Malden, Oxford.
; Stein et al., 2009Stein, M., Peel, J., Siveter, D., Williams, M. (2009) Isoxys (Arthropoda) with preserved soft anatomy from the Sirius Passet Lagerstätte, lower Cambrian of North Greenland. Lethaia 43, 258–265.
; Vinther et al., 2014Vinther, J., Stein, M., Longrich, N.R., Harper, D.A. (2014) A suspension-feeding anomalocarid from the Early Cambrian. Nature 507, 496–499.
). Therefore, we consider that this oxygenation episode reflects the first invasion of larger zooplankton in the pelagic zone that triggered an increase in the sinking rate and compaction of organic matter. Today, the export of organic matter from the photic zone (<200 m depth) — a process referred to as the biological pump — occurs as sinking molts, faecal matter, carcasses, and skeletons (Alldredge et al., 1993Alldredge, A.L., Passow, U., Logan, B.E. (1993) The abundance and significance of a class of large, transparent organic particles in the ocean. Deep Sea Research I 40, 1131–1140.
; Hedges and Keil, 1995Hedges, J.L., Keil, R.G. (1995) Sedimentary organic matter preservation: an assessment and speculative synthesis. Marine Chemistry 49, 81–115.
). The sinking velocity of a particle in the ocean is a quadratic function of its size. Therefore, a small increase in the mean size of particulate organic matter would have caused the rates of water column remineralisation to decrease, so that less O2 was consumed in the water column and a more gentle O2 gradient was established below the photic zone (Fig. 3, Meyer et al., 2016Meyer, K.M., Ridgwell, A., Payne, J.L. (2016) The influence of the biological pump on ocean chemistry: implications for long-term trends in marine redox chemistry, the global carbon cycle, and marine animal ecosystems. Geobiology 14, 207–219.
). Consequently, more organic matter would have been exported to the seafloor resulting in enhanced rates of organic carbon and pyrite burial.
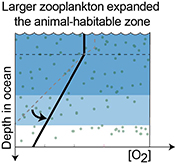
Figure 3 Conceptual model for the episodic expansion of the oxygenation zone in the oceans. The emergence of bilaterian animals (a-b) increased sediment mixing via bioturbation causing atmospheric pO2 to decline. The oxygenation zone contracts until (c) a rapid increase in the sinking rate of organic matter changes O2 consumption rates in the upper water column. (d) This accelerates organic carbon export to the sediments and delivers more food and O2 to the benthos over wider areas of the seafloor. Enhanced bioturbation promotes atmospheric pO2 decline, and re-stabilises the ocean in a more reducing state. Arrows and numbers illustrate organic export fluxes in one scenario (details in Table S-11). For simplicity, the organic C export increases in one step with the emergence of larger faecal pellets. Quantitative estimates for organic carbon export and remineralisation are derived from the coupled C and S isotope modelling (see Supplementary Information S5).
To quantify the potential consequences of faster sinking rates on organic carbon export (JRAIN) onto the seafloor, we utilise the δ13C and δ34S data and a simple biogeochemical model for the coupled marine C and S cycles. Organic carbon export fuels both organic carbon burial (JORG = JRAIN - JREMIN) and remineralisation in sediments (JREMIN). In this model, pyrite burial is proportional to the remineralisation flux (JPY = α · JREMIN) because microbial sulphate reduction accounts for the major part of organic remineralisation in sediments and a fraction of its byproduct, sulphide, reacts with available Fe compounds to form pyrite (see Supplementary Information for model details). With this formulation (α constant), we find that a 3–6 fold increase in the organic carbon rain rate is sufficient to increase δ13C (0 to 3 ‰) and δ34S (28 to 40 ‰) simultaneously. This can be achieved with only a 1.7–2.5 fold increase in the mean of the size distribution of sinking organic matter particulates, assuming similar density and shape for the particulates before and after the invasion of larger zooplankton. We consider this as a minimum estimate, if a greater portion of larger faecal pellets do not aggregate (Butterfield, 1997
Butterfield, N.J. (1997) Ecology and the Proterozoic-Phanerozoic Transition. Paleobiology 23, 247–262.
). However, it shows that even a modest size increase potentially influences the global biogeochemical cycles.The evolutionary history of animals over the Neoproterozoic-Cambrian transition suggests a stepwise increase in their overall size and their digestive tracts, which would have enhanced the biological pump (Logan et al., 1995
Logan, G.A., Hayes, J.M., Hieshima, G.B., Summons, R.E. (1995) Terminal Proterozoic reorganization of biogeochemical cycles. Nature 376, 53–56.
; Butterfield, 2009Butterfield, N.J. (2009) Oxygen, animals and oceanic ventilation: an alternative view. Geobiology 7, 1–7.
; Lenton et al., 2014Lenton, T.M., Boyle, R.A., Poulton, S.W., Shields-Zhou, G.A., Butterfield, N.J. (2014) Co-evolution of eukaryotes and ocean oxygenation in the Neoproterozoic era. Nature Geoscience 7, 257–265.
). Biomarker evidence suggests a fundamental shift in the preservation state of marine organic matter with abundant faecal matter in sedimentary rocks younger than ~517 Ma compared to similar rocks older than ~565 Ma (Logan et al., 1995Logan, G.A., Hayes, J.M., Hieshima, G.B., Summons, R.E. (1995) Terminal Proterozoic reorganization of biogeochemical cycles. Nature 376, 53–56.
). Although the abundance of pelagic animal fauna through the Cambrian Stage 2–3 interval is not known, it is apparent that the maximum size of pelagic heterotrophic organisms and their digestive tracts increased by three orders of magnitude from the Ediacaran into the Cambrian. Heterotrophic consumers such as micro- and mesozooplankton (20–200 µm) evolved in the latest Ediacaran (635–542 Ma) (Perrier et al., 2015Perrier, V., Williams, M., Siveter, D.J. (2015) The fossil record and palaeoenvironmental significance of marine arthropod zooplankton. Earth-Science Reviews 146, 146–162.
). The fossil record indicates that animals of probable chaetognath affinity ('protoconodonts') a few millimetres in size or larger swam in the early Fortunian ocean (>535 Ma), and that large macrozooplankton (i.e. bivalved arthropod Isoxys) up to 45 mm had appeared in the earliest Stage 3 (~520 Ma) (Ivantsov, 1990Ivantsov, A.Y. (1990) The first findings of phyllocarida in the lower Cambrian deposits of Yakutia Russian SFSR USSR. Paleontologicheskii Zhurnal, 130–132.
; Hou, 2004Hou, X.G., Aldridge, R.J., Bergström, J., Siveter, D.J., Siveter, D.J., Feng, X.H. (2004) The Cambrian fossils of Chengjiang, China - the flowering of early animal life. Blackwell Publishing, Malden, Oxford.
; Stein et al., 2009Stein, M., Peel, J., Siveter, D., Williams, M. (2009) Isoxys (Arthropoda) with preserved soft anatomy from the Sirius Passet Lagerstätte, lower Cambrian of North Greenland. Lethaia 43, 258–265.
). However, it says nothing about when various types of zooplankton became ecologically important. Rather, we suggest that a stepwise increase in the size of zooplankton is a plausible trigger for the reorganisation of Earth's marine biogeochemical cycles and, consequently, the earliest Cambrian Stage 3 oxygenation episode. By implication, earlier steps in animal evolution may have also led to oxygenation events preserved in the geochemical record during the Ediacaran–Cambrian transition (see below).Given that the geochemical evidence suggests that the Cambrian Stage 2–3 oxygenation episode was brief, a stabilising feedback must have acted to counterbalance marine oxygenation. Current models for the evolving biogeochemical cycles in the Cambrian have not included such a rapid feedback mechanism (Bergman et al., 2004
Bergman, N.M., Lenton, T.M., Watson, A.J. (2004) COPSE: A new model of biogeochemical cycling over Phanerozoic time. American Journal of Science 304, 397–437.
; Berner, 2006Berner, R.A. (2006) GEOCARBSULF: A combined model for Phanerozoic atmospheric O2 and CO2. Geochimica et Cosmochimica Acta 70, 5653–5664.
). Evidence from bioturbation indices (Mangano and Buatois, 2014Mangano, M.G., Buatois, L.A. (2014) Decoupling of body-plan diversification and ecological structuring during the Ediacaran-Cambrian transition: evolutionary and geobiological feedbacks. Proceedings of the Royal Society B. Biological Science 281, 20140038.
) and Earth system modelling (Canfield and Farquhar, 2009Canfield, D.E., Farquhar, J. (2009) Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proceedings of the National Academy of Sciences USA 106, 8123–8127.
; Boyle et al., 2014Boyle, R.A., Dahl, T.W., Dale, A.W., Shields-Zhou, G.A., Zhu, M., Brasier, M.D., Canfield, D.E., Lenton, T.M. (2014) Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nature Geoscience 7, 671–676.
) suggest that the Cambrian Stage 3 oxygenation episode occurred during an apparent atmospheric pO2 decline resulting from increased mixing of marine sediments by animals. Since the early Cambrian Stage 2 (~530 Ma), animals had evolved the ability to burrow deeper into sediments acting to lower marine P availability, organic productivity, organic carbon burial, and hence the main source of atmospheric pO2 (Boyle et al., 2014Boyle, R.A., Dahl, T.W., Dale, A.W., Shields-Zhou, G.A., Zhu, M., Brasier, M.D., Canfield, D.E., Lenton, T.M. (2014) Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nature Geoscience 7, 671–676.
). The emerging larger pelagic fauna accelerated this feedback mechanism, since the enhanced biological pump would have both increased the food supply and food quality for benthic heterotrophic organisms and led to more fully oxygenated conditions in the water column below the photic zone, thereby opening new ecospace for sediment-mixing animals over wider areas of the continental shelves. Subsequently, this focusing of organic matter at the seafloor increased overall rate of bioturbation, organic carbon remineralisation and oxygen consumption over larger areas of the seafloor and, ultimately, a decline in atmospheric pO2 that again limited the size of the oxygenated zones in the oceans (Fig. 3). It is notable that for this sequence of feedbacks to respond over the time scale of the Cambrian Stage 2–3 oxygenation episode (1.3 ± 0.8 Myr (Maloof et al., 2010Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
), see calculation in the Supplementary Information), atmospheric O2 inventory must have been significantly smaller than today in order to produce an excursion of the right duration. We derive an order of magnitude estimate for the atmospheric pO2 level at the Cambrian Stage 2-3 boundary of between 4 ± 2 and 7 ± 4 atm % from the duration of the falling limb isotope excursions, assuming the global burial rate of marine organic carbon was the same as today. We also assume that anoxia returns as atmospheric pO2 levels decline due to less organic carbon burial over the course of ~1/4 to ~1/2 the duration of the full δ13C excursion (~325 ± 200 and ~650 ± 400 kyr). This atmospheric pO2 estimate scales linearly with global organic carbon burial flux, and requires that the acceleration of the biological pump (by faecal pellets) and the subsequent migration of the sediment-dwelling taxa are essentially instantaneous (<<100 kyr). This atmospheric pO2 level is well above the metabolic need for some animals (Pasteur limit ~0.2 atm %) (Mills and Canfield, 2014Mills, D.B., Canfield, D.E. (2014) Oxygen and animal evolution: Did a rise of atmospheric oxygen "trigger" the origin of animals? Bioessays 36, 1145–1155.
), but not sufficiently high to oxygenate the deep oceans permanently (Lyons et al., 2014Lyons, T.W., Reinhard, C.T., Planavsky, N.J. (2014) The rise of oxygen in Earth's early ocean and atmosphere. Nature 506, 307–315.
) and it conforms with the idea that animal ecosystems could have become self-limiting in terms of determining the size of the habitable ecospace in the oceans (Sperling et al., 2013Sperling, E.A., Frieder, C.A., Raman, A.V., Girguis, P.R., Levin, L.A., Knoll, A.H. (2013) Oxygen, ecology, and the Cambrian radiation of animals. Proceedings of the National Academy of Sciences 110, 13446–13451.
; Boyle et al., 2014Boyle, R.A., Dahl, T.W., Dale, A.W., Shields-Zhou, G.A., Zhu, M., Brasier, M.D., Canfield, D.E., Lenton, T.M. (2014) Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nature Geoscience 7, 671–676.
).top
Acknowledgements
We thank N. Jensen, T. Balic-Zunic, H. Almind, N.J.B. Kristensen (UCPH) for laboratory assistance, S. Bengtson (SMNH) for field assistance in 1996 with AK, and T.J. Algeo, C. Li and one anonymous reviewer for insightful comments. Funding for this project was provided by a grant from the VILLUM Foundation (VKR023127) to TWD, and from the Danish Agency for Science, Technology and Innovation (grant number 12-125692) to JNC as well as grants from the Danish National Research Foundation (grant number DNRF97) and from the European Research Council (ERC Consolidator grant agreement 616027-STARDUST2ASTEROIDS) to MB. Fieldwork was financially supported by grants from the Royal Swedish Academy of Sciences (KVA), the Swedish Natural Science Research Council (NFR), and the Swedish Research Council (VR).
Editor: Liane G. Benning
top
Author Contributions
AK collected the samples. TWD conceived the idea, designed the study, interpreted the data and created the models. TWD, JNC, BCG, SFM and MB analysed the samples and wrote the manuscript with significant contributions from all co-authors.
top
References
Alldredge, A.L., Passow, U., Logan, B.E. (1993) The abundance and significance of a class of large, transparent organic particles in the ocean. Deep Sea Research I 40, 1131–1140.
 Show in context
Show in context Today, the export of organic matter from the photic zone (<200 m depth) — a process referred to as the biological pump — occurs as sinking molts, faecal matter, carcasses, and skeletons (Alldredge et al., 1993; Hedges and Keil, 1995).
View in article
Bergman, N.M., Lenton, T.M., Watson, A.J. (2004) COPSE: A new model of biogeochemical cycling over Phanerozoic time. American Journal of Science 304, 397–437.
 Show in context
Show in context Current models for the evolving biogeochemical cycles in the Cambrian have not included such a rapid feedback mechanism (Bergman et al., 2004; Berner, 2006).
View in article
Berner, R.A. (2006) GEOCARBSULF: A combined model for Phanerozoic atmospheric O2 and CO2. Geochimica et Cosmochimica Acta 70, 5653–5664.
 Show in context
Show in context Current models for the evolving biogeochemical cycles in the Cambrian have not included such a rapid feedback mechanism (Bergman et al., 2004; Berner, 2006).
View in article
Boyle, R.A., Dahl, T.W., Dale, A.W., Shields-Zhou, G.A., Zhu, M., Brasier, M.D., Canfield, D.E., Lenton, T.M. (2014) Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nature Geoscience 7, 671–676.
 Show in context
Show in context Evidence from bioturbation indices (Mangano and Buatois, 2014) and Earth system modelling (Canfield and Farquhar, 2009; Boyle et al., 2014) suggest that the Cambrian Stage 3 oxygenation episode occurred during an apparent atmospheric pO2 decline resulting from increased mixing of marine sediments by animals.
View in article
Since the early Cambrian Stage 2 (~530 Ma), animals had evolved the ability to burrow deeper into sediments acting to lower marine P availability, organic productivity, organic carbon burial, and hence the main source of atmospheric pO2 (Boyle et al., 2014).
View in article
This atmospheric pO2 level is well above the metabolic need for some animals (Pasteur limit ~0.2 atm %) (Mills and Canfield, 2014), but not sufficiently high to oxygenate the deep oceans permanently (Lyons et al., 2014) and it conforms with the idea that animal ecosystems could have become self-limiting in terms of determining the size of the habitable ecospace in the oceans (Sperling et al., 2013; Boyle et al., 2014).
View in article
Brennecka, G.A., Herrmann, A.D., Algeo, T.J., Anbar, A.D. (2011) Rapid expansion of oceanic anoxia immediately before the end-Permian mass extinction. Proceedings of the National Academy of Sciences 108, 17631–17634.
 Show in context
Show in context The δ238U proxy has been utilised to track past global ocean redox during three known oceanic anoxic events (Montoya-Pino et al., 2010; Brennecka et al., 2011; Dahl et al., 2014; Elrick et al., 2016; Lau et al., 2016), where anoxic water masses expanded over larger areas of the seafloor and caused negative δ238U excursions.
View in article
This scenario compares to the ocean state during the anoxic expansion associated with the end-Permian extinction (Brennecka et al., 2011).
View in article
Butterfield, N.J. (1997) Ecology and the Proterozoic-Phanerozoic Transition. Paleobiology 23, 247–262.
 Show in context
Show in context We consider this as a minimum estimate, if a greater portion of larger faecal pellets do not aggregate (Butterfield, 1997).
View in article
Butterfield, N.J. (2009) Oxygen, animals and oceanic ventilation: an alternative view. Geobiology 7, 1–7.
 Show in context
Show in context The evolutionary history of animals over the Neoproterozoic-Cambrian transition suggests a stepwise increase in their overall size and their digestive tracts, which would have enhanced the biological pump (Logan et al., 1995; Butterfield, 2009; Lenton et al., 2014).
View in article
Canfield, D.E., Farquhar, J. (2009) Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proceedings of the National Academy of Sciences USA 106, 8123–8127.
 Show in context
Show in context Evidence from bioturbation indices (Mangano and Buatois, 2014) and Earth system modelling (Canfield and Farquhar, 2009; Boyle et al., 2014) suggest that the Cambrian Stage 3 oxygenation episode occurred during an apparent atmospheric pO2 decline resulting from increased mixing of marine sediments by animals.
View in article
Chen, X., Ling, H.F., Vance, D., Shields-Zhou, G.A., Zhu, M., Poulton, S.W., Och, L.M., Jiang, S.Y., Li, D., Cremonese, L., Archer, C. (2015) Rise to modern levels of ocean oxygenation coincided with the Cambrian radiation of animals. Nature Communications 6, 7142.
 Show in context
Show in context Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008; Wen et al., 2011; Xu et al., 2012; Chen et al., 2015; Kendall et al., 2015; Wen et al., 2015).
View in article
The last positive δ98Mo excursion is broadly correlated to the first appearance of trilobites in China, strong Mo enrichments and with the oxygenation event reported here (Dahl et al., 2010; Xu et al., 2012; Chen et al., 2015; Wen et al., 2015; Jin et al., 2016).
View in article
This prediction is in good agreement with the maximum values observed in the δ98Mo record during this time interval (Lehmann et al., 2007; Chen et al., 2015; Wen et al., 2015) (Fig. 2).
View in article
As such, the oxygenation history of the early Cambrian ocean appears more dynamic than previously thought (e.g., Dahl et al., 2010; Sperling et al., 2013; Chen et al., 2015).
View in article
Chen, X., Romaniello, S.J., Herrmann, A.D., Wasylenki, L.E., Anbar, A.D. (2016) Uranium isotope fractionation during coprecipitation with aragonite and calcite. Geochimica et Cosmochimica Acta 188, 189–207.
 Show in context
Show in context The difference between abiotic and biotic precipitation of calcite δ238U is predicted to induce a ~0.1 ‰ offset from seawater (Chen et al., 2016).
View in article
Dahl, T.W., Hammarlund, E.U., Anbar, A.D., Bond, D.P.G., Gill, B.C., Gordon, G.W., Knoll, A.H., Nielsen, A.T., Schovsbo, N.H., Canfield, D.E. (2010) Devonian rise in atmospheric oxygen correlated to the radiations of terrestrial plants and large predatory fish. Proceedings of the National Academy of Sciences 107, 17911–17915.
 Show in context
Show in context The last positive δ98Mo excursion is broadly correlated to the first appearance of trilobites in China, strong Mo enrichments and with the oxygenation event reported here (Dahl et al., 2010; Xu et al., 2012; Chen et al., 2015; Wen et al., 2015; Jin et al., 2016).
View in article
As such, the oxygenation history of the early Cambrian ocean appears more dynamic than previously thought (e.g., Dahl et al., 2010; Sperling et al., 2013; Chen et al., 2015).
View in article
Dahl, T.W., Boyle, R.A., Canfield, D.E., Connelly, J.N., Gill, B.C., Lenton, T.M., Bizzarro, M. (2014) Uranium isotopes distinguish two geochemically distinct stages during the later Cambrian SPICE event. Earth and Planetary Science Letters 401, 313–326.
 Show in context
Show in context This is possible due to the long residence time and uniform δ238U of uranium in the modern ocean and predicted for the Cambrian ocean (Weyer et al., 2008; Dahl et al., 2014; Tissot and Dauphas, 2015).
View in article
The δ238U proxy has been utilised to track past global ocean redox during three known oceanic anoxic events (Montoya-Pino et al., 2010; Brennecka et al., 2011; Dahl et al., 2014; Elrick et al., 2016; Lau et al., 2016), where anoxic water masses expanded over larger areas of the seafloor and caused negative δ238U excursions.
View in article
Similar parallel positive carbon and sulphur isotope excursions during the late Cambrian SPICE event (Gill et al., 2011; Dahl et al., 2014) and the Botoman Sinsk event were interpreted to represent a period of enhanced organic carbon and pyrite burial (Zhuravlev and Wood, 1996).
View in article
Dunk, R.M., Mills, R.A., Jenkins, W.J. (2002) A reevaluation of the oceanic uranium budget for the Holocene. Chemical Geology 190, 45–67.
 Show in context
Show in context If the anoxic proportion of global U burial (fU) today is 12–25 % (Morford and Emerson, 1999; Dunk et al., 2002; Noordmann et al., 2016), and anoxic settings impart a +0.5 ± 0.1 ‰ net isotope offset from overlying seawater, this implies that the average isotope fractionation between seawater and all other oxic U sinks (ΔOTHER) is –0.02 ± 0.05 ‰.
View in article
Elrick, M., Polyak, V., Algeo, T.J., Romaniello, S., Asmerom, Y., Herrmann, A.D., Anbar, A.D., Zhao, L., Chen, Z.-Q. (2016) Global-ocean redox variation during the middle-late Permian through Early Triassic based on uranium isotope and Th/U trends of marine carbonates. Geology, G38585.1.
 Show in context
Show in context The δ238U proxy has been utilised to track past global ocean redox during three known oceanic anoxic events (Montoya-Pino et al., 2010; Brennecka et al., 2011; Dahl et al., 2014; Elrick et al., 2016; Lau et al., 2016), where anoxic water masses expanded over larger areas of the seafloor and caused negative δ238U excursions.
View in article
Gill, B.C., Lyons, T.W., Young, S.A., Kump, L.R., Knoll, A.H., Saltzman, M.R. (2011) Geochemical evidence for widespread euxinia in the later Cambrian ocean. Nature 469, 80–83.
 Show in context
Show in context Similar parallel positive carbon and sulphur isotope excursions during the late Cambrian SPICE event (Gill et al., 2011; Dahl et al., 2014) and the Botoman Sinsk event were interpreted to represent a period of enhanced organic carbon and pyrite burial (Zhuravlev and Wood, 1996).
View in article
Hedges, J.L., Keil, R.G. (1995) Sedimentary organic matter preservation: an assessment and speculative synthesis. Marine Chemistry 49, 81–115.
 Show in context
Show in context Today, the export of organic matter from the photic zone (<200 m depth) — a process referred to as the biological pump — occurs as sinking molts, faecal matter, carcasses, and skeletons (Alldredge et al., 1993; Hedges and Keil, 1995).
View in article
Hou, X.G., Aldridge, R.J., Bergström, J., Siveter, D.J., Siveter, D.J., Feng, X.H. (2004) The Cambrian fossils of Chengjiang, China - the flowering of early animal life. Blackwell Publishing, Malden, Oxford.
 Show in context
Show in context The Cambrian Stage 2–3 event coincides with the onset of the first major diversification of arthropods, which predates by a few million years the first appearance of macrozooplankton and suspension-feeding anomalocarids (Hou, 2004; Stein et al., 2009; Vinther et al., 2014).
View in article
The fossil record indicates that animals of probable chaetognath affinity ('protoconodonts') a few millimetres in size or larger swam in the early Fortunian ocean (>535 Ma), and that large macrozooplankton (i.e. bivalved arthropod Isoxys) up to 45 mm had appeared in the earliest Stage 3 (~520 Ma) (Ivantsov, 1990; Hou, 2004; Stein et al., 2009).
View in article
Ivantsov, A.Y. (1990) The first findings of phyllocarida in the lower Cambrian deposits of Yakutia Russian SFSR USSR. Paleontologicheskii Zhurnal, 130–132.
 Show in context
Show in context The fossil record indicates that animals of probable chaetognath affinity ('protoconodonts') a few millimetres in size or larger swam in the early Fortunian ocean (>535 Ma), and that large macrozooplankton (i.e. bivalved arthropod Isoxys) up to 45 mm had appeared in the earliest Stage 3 (~520 Ma) (Ivantsov, 1990; Hou, 2004; Stein et al., 2009).
View in article
Jin, C., Li, C., Algeo, T.J., Planavsky, N.J., Cui, H., Yang, X., Zhao, Y., Zhang, X., Xie, S. (2016) A highly redox-heterogeneous ocean in South China during the early Cambrian (∼529–514 Ma): Implications for biota-environment co-evolution. Earth and Planetary Science Letters 441, 38–51.
 Show in context
Show in context The last positive δ98Mo excursion is broadly correlated to the first appearance of trilobites in China, strong Mo enrichments and with the oxygenation event reported here (Dahl et al., 2010; Xu et al., 2012; Chen et al., 2015; Wen et al., 2015; Jin et al., 2016).
View in article
Similarly, detailed studies of the bottom water redox conditions in the Nanhua Basin, South China, suggest that oxygenated waters also invaded shallower part of the basin later in the Stage 3 (Jin et al. 2016).
View in article
Kendall, B., Komiya, T., Lyons, T.W., Bates, S.M., Gordon, G.W., Romaniello, S.J., Jiang, G., Creaser, R.A., Xiao, S., McFadden, K., Sawaki, Y., Tahata, M., Shu, D., Han, J., Li, Y., Chu, X., Anbar, A.D. (2015) Uranium and molybdenum isotope evidence for an episode of widespread ocean oxygenation during the late Ediacaran Period. Geochimica et Cosmochimica Acta 156, 173–193.
 Show in context
Show in context Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008; Wen et al., 2011; Xu et al., 2012; Chen et al., 2015; Kendall et al., 2015; Wen et al., 2015).
View in article
This implies that earlier positive δ98Mo excursions (~2 ‰) in Terreneuvian phosphorite deposits (Wen et al., 2011), and perhaps in the latest Ediacaran (Kendall et al., 2015), represent episodic events rather than persistent ocean oxygenation.
View in article
Kouchinsky, A., Bengtson, S., Pavlov, V., Runnegar, B., Torssander, P., Young, E., Ziegler, K. (2007) Carbon isotope stratigraphy of the Precambrian–Cambrian Sukharikha River section, northwestern Siberian platform. Geological Magazine 144, 1–10.
 Show in context
Show in context Figure 1 [...] Carbon isotope data from carbonate (δ13CCARB) is taken from Kouchinsky et al. (2007).
View in article
Kouchinsky, A., Bengtson, S., Runnegar, B., Skovsted, C., Steiner, M., Vendrasco, M. (2012) Chronology of early Cambrian biomineralization. Geological Magazine 149, 221–251.
 Show in context
Show in context Our new δ238U data of carbonate-associated uranium comes from limestones collected from the Siberian Platform across the provisional Cambrian Stage 2–3 boundary (~521 to 520 million years ago) (Fig. 1), when animals that shed their exoskeleton (ecdysozoa) began to diversify (Maloof et al., 2010; Kouchinsky et al., 2012).
View in article
Lau, K.V., Maher, K., Altiner, D., Kelley, B.M., Kump, L.R., Lehrmann, D.J., Silva-Tamayo, J.C., Weaver, K.L., Yu, M., Payne, J.L. (2016) Marine anoxia and delayed Earth system recovery after the end-Permian extinction. Proceedings of the National Academy of Science USA 113, 2360–2365.
 Show in context
Show in context The δ238U proxy has been utilised to track past global ocean redox during three known oceanic anoxic events (Montoya-Pino et al., 2010; Brennecka et al., 2011; Dahl et al., 2014; Elrick et al., 2016; Lau et al., 2016), where anoxic water masses expanded over larger areas of the seafloor and caused negative δ238U excursions.
View in article
Lehmann, B., Nägler, T.F., Holland, H.D., Wille, M., Mao, J., Pan, J., Ma, D., Dulski, P. (2007) Highly metalliferous carbonaceous shale and Early Cambrian seawater. Geology 35, 403.
 Show in context
Show in context This prediction is in good agreement with the maximum values observed in the δ98Mo record during this time interval (Lehmann et al., 2007; Chen et al., 2015; Wen et al., 2015) (Fig. 2).
View in article
Lenton, T.M., Boyle, R.A., Poulton, S.W., Shields-Zhou, G.A., Butterfield, N.J. (2014) Co-evolution of eukaryotes and ocean oxygenation in the Neoproterozoic era. Nature Geoscience 7, 257–265.
 Show in context
Show in context The evolutionary history of animals over the Neoproterozoic-Cambrian transition suggests a stepwise increase in their overall size and their digestive tracts, which would have enhanced the biological pump (Logan et al., 1995; Butterfield, 2009; Lenton et al., 2014).
View in article
Logan, G.A., Hayes, J.M., Hieshima, G.B., Summons, R.E. (1995) Terminal Proterozoic reorganization of biogeochemical cycles. Nature 376, 53–56.
 Show in context
Show in context The evolutionary history of animals over the Neoproterozoic-Cambrian transition suggests a stepwise increase in their overall size and their digestive tracts, which would have enhanced the biological pump (Logan et al., 1995; Butterfield, 2009; Lenton et al., 2014).
View in article
Biomarker evidence suggests a fundamental shift in the preservation state of marine organic matter with abundant faecal matter in sedimentary rocks younger than ~517 Ma compared to similar rocks older than ~565 Ma (Logan et al., 1995).
View in article
Lyons, T.W., Reinhard, C.T., Planavsky, N.J. (2014) The rise of oxygen in Earth's early ocean and atmosphere. Nature 506, 307–315.
 Show in context
Show in context This atmospheric pO2 level is well above the metabolic need for some animals (Pasteur limit ~0.2 atm %) (Mills and Canfield, 2014), but not sufficiently high to oxygenate the deep oceans permanently (Lyons et al., 2014) and it conforms with the idea that animal ecosystems could have become self-limiting in terms of determining the size of the habitable ecospace in the oceans (Sperling et al., 2013; Boyle et al., 2014).
View in article
Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
 Show in context
Show in context Our new δ238U data of carbonate-associated uranium comes from limestones collected from the Siberian Platform across the provisional Cambrian Stage 2–3 boundary (~521 to 520 million years ago) (Fig. 1), when animals that shed their exoskeleton (ecdysozoa) began to diversify (Maloof et al., 2010; Kouchinsky et al., 2012).
View in article
A perturbation in the marine carbon cycle is expressed at this time as a large positive carbon isotope excursion recognised globally and in all studied sections; geological maps and stratigraphic sections are shown in Figures S-1 and S-2 (Maloof et al., 2010).
View in article
Figure 1 [...] Sulphur and uranium isotope data are from carbonate-associated sulphate (δ34SCAS) and uranium (δ238UCAU), respectively. Age assignments derived from correlations to the carbon isotope stratigraphy and the age model of Maloof et al. (2010).
View in article
It is notable that for this sequence of feedbacks to respond over the time scale of the Cambrian Stage 2–3 oxygenation episode (1.3 ± 0.8 Myr (Maloof et al., 2010), see calculation in the Supplementary Information), atmospheric O2 inventory must have been significantly smaller than today in order to produce an excursion of the right duration.
View in article
Mangano, M.G., Buatois, L.A. (2014) Decoupling of body-plan diversification and ecological structuring during the Ediacaran-Cambrian transition: evolutionary and geobiological feedbacks. Proceedings of the Royal Society B. Biological Science 281, 20140038.
 Show in context
Show in context Evidence from bioturbation indices (Mangano and Buatois, 2014) and Earth system modelling (Canfield and Farquhar, 2009; Boyle et al., 2014) suggest that the Cambrian Stage 3 oxygenation episode occurred during an apparent atmospheric pO2 decline resulting from increased mixing of marine sediments by animals.
View in article
Meyer, K.M., Ridgwell, A., Payne, J.L. (2016) The influence of the biological pump on ocean chemistry: implications for long-term trends in marine redox chemistry, the global carbon cycle, and marine animal ecosystems. Geobiology 14, 207–219.
 Show in context
Show in context Therefore, a small increase in the mean size of particulate organic matter would have caused the rates of water column remineralisation to decrease, so that less O2 was consumed in the water column and a more gentle O2 gradient was established below the photic zone (Fig. 3, Meyer et al., 2016).
View in article
Mills, D.B., Canfield, D.E. (2014) Oxygen and animal evolution: Did a rise of atmospheric oxygen "trigger" the origin of animals? Bioessays 36, 1145–1155.
 Show in context
Show in context This atmospheric pO2 level is well above the metabolic need for some animals (Pasteur limit ~0.2 atm %) (Mills and Canfield, 2014), but not sufficiently high to oxygenate the deep oceans permanently (Lyons et al., 2014) and it conforms with the idea that animal ecosystems could have become self-limiting in terms of determining the size of the habitable ecospace in the oceans (Sperling et al., 2013; Boyle et al., 2014).
View in article
Montoya-Pino, C., Weyer, S., Anbar, A.D., Pross, J., Oschmann, W., van de Schootbrugge, B., Arz, H.W. (2010) Global enhancement of ocean anoxia during Oceanic Anoxic Event 2: A quantitative approach using U isotopes. Geology 38, 315–318.
 Show in context
Show in context The δ238U proxy has been utilised to track past global ocean redox during three known oceanic anoxic events (Montoya-Pino et al., 2010; Brennecka et al., 2011; Dahl et al., 2014; Elrick et al., 2016; Lau et al., 2016), where anoxic water masses expanded over larger areas of the seafloor and caused negative δ238U excursions.
View in article
Morford, J.L., Emerson, S. (1999) The geochemistry of redox sensitive trace metals in sediments. Geochimica Et Cosmochimica Acta 63, 1735–1750.
 Show in context
Show in context If the anoxic proportion of global U burial (fU) today is 12–25 % (Morford and Emerson, 1999; Dunk et al., 2002; Noordmann et al., 2016), and anoxic settings impart a +0.5 ± 0.1 ‰ net isotope offset from overlying seawater, this implies that the average isotope fractionation between seawater and all other oxic U sinks (ΔOTHER) is –0.02 ± 0.05 ‰.
View in article
Noordmann, J., Weyer, S., Georg, R.B., Jons, S., Sharma, M. (2016) 238U/235U isotope ratios of crustal material, rivers and products of hydrothermal alteration: new insights on the oceanic U isotope mass balance. Isotopes in Environmental Health Studies 52, 141–163.
 Show in context
Show in context The modern ocean is at steady state with δ238U at –0.39 ± 0.01 ‰ and estimates for the average oceanic input range from –0.30 ‰ to –0.27 ‰ (Tissot and Dauphas, 2015; Noordmann et al., 2016).
View in article
If the anoxic proportion of global U burial (fU) today is 12–25 % (Morford and Emerson, 1999; Dunk et al., 2002; Noordmann et al., 2016), and anoxic settings impart a +0.5 ± 0.1 ‰ net isotope offset from overlying seawater, this implies that the average isotope fractionation between seawater and all other oxic U sinks (ΔOTHER) is –0.02 ± 0.05 ‰.
View in article
Perrier, V., Williams, M., Siveter, D.J. (2015) The fossil record and palaeoenvironmental significance of marine arthropod zooplankton. Earth-Science Reviews 146, 146–162.
 Show in context
Show in context Heterotrophic consumers such as micro- and mesozooplankton (20–200 µm) evolved in the latest Ediacaran (635–542 Ma) (Perrier et al., 2015).
View in article
Sperling, E.A., Frieder, C.A., Raman, A.V., Girguis, P.R., Levin, L.A., Knoll, A.H. (2013) Oxygen, ecology, and the Cambrian radiation of animals. Proceedings of the National Academy of Sciences 110, 13446–13451.
 Show in context
Show in context As such, the oxygenation history of the early Cambrian ocean appears more dynamic than previously thought (e.g., Dahl et al., 2010; Sperling et al., 2013; Chen et al., 2015).
View in article
This atmospheric pO2 level is well above the metabolic need for some animals (Pasteur limit ~0.2 atm %) (Mills and Canfield, 2014), but not sufficiently high to oxygenate the deep oceans permanently (Lyons et al., 2014) and it conforms with the idea that animal ecosystems could have become self-limiting in terms of determining the size of the habitable ecospace in the oceans (Sperling et al., 2013; Boyle et al., 2014).
View in article
Stein, M., Peel, J., Siveter, D., Williams, M. (2009) Isoxys (Arthropoda) with preserved soft anatomy from the Sirius Passet Lagerstätte, lower Cambrian of North Greenland. Lethaia 43, 258–265.
 Show in context
Show in context The Cambrian Stage 2–3 event coincides with the onset of the first major diversification of arthropods, which predates by a few million years the first appearance of macrozooplankton and suspension-feeding anomalocarids (Hou, 2004; Stein et al., 2009; Vinther et al., 2014).
View in article
The fossil record indicates that animals of probable chaetognath affinity ('protoconodonts') a few millimetres in size or larger swam in the early Fortunian ocean (>535 Ma), and that large macrozooplankton (i.e. bivalved arthropod Isoxys) up to 45 mm had appeared in the earliest Stage 3 (~520 Ma) (Ivantsov, 1990; Hou, 2004; Stein et al., 2009).
View in article
Tissot, F.L.H., Dauphas, N. (2015) Uranium isotopic compositions of the crust and ocean: Age corrections, U budget and global extent of modern anoxia. Geochimica et Cosmochimica Acta 167, 113–143.
 Show in context
Show in context This is possible due to the long residence time and uniform δ238U of uranium in the modern ocean and predicted for the Cambrian ocean (Weyer et al., 2008; Dahl et al., 2014; Tissot and Dauphas, 2015).
View in article
The end-Stage 2 samples carry low δ238U values of –0.65 ‰, increasing stratigraphically to a value of –0.45 ‰ that approaches the modern oxygenated oceans, –0.39 ± 0.01 ‰ (Tissot and Dauphas, 2015), before again returning in two steps to –0.7 ‰.
View in article
The modern ocean is at steady state with δ238U at –0.39 ± 0.01 ‰ and estimates for the average oceanic input range from –0.30 ‰ to –0.27 ‰ (Tissot and Dauphas, 2015; Noordmann et al., 2016).
View in article
Vinther, J., Stein, M., Longrich, N.R., Harper, D.A. (2014) A suspension-feeding anomalocarid from the Early Cambrian. Nature 507, 496–499.
 Show in context
Show in context The Cambrian Stage 2–3 event coincides with the onset of the first major diversification of arthropods, which predates by a few million years the first appearance of macrozooplankton and suspension-feeding anomalocarids (Hou, 2004; Stein et al., 2009; Vinther et al., 2014).
View in article
Wen, H., Carignan, J., Zhang, Y., Fan, H., Cloquet, C., Liu, S. (2011) Molybdenum isotopic records across the Precambrian-Cambrian boundary. Geology 39, 775–778.
 Show in context
Show in context Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008; Wen et al., 2011; Xu et al., 2012; Chen et al., 2015; Kendall et al., 2015; Wen et al., 2015).
View in article
This implies that earlier positive δ98Mo excursions (~2 ‰) in Terreneuvian phosphorite deposits (Wen et al., 2011), and perhaps in the latest Ediacaran (Kendall et al., 2015), represent episodic events rather than persistent ocean oxygenation.
View in article
Wen, H., Fan, H., Zhang, Y., Cloquet, C., Carignan, J. (2015) Reconstruction of early Cambrian ocean chemistry from Mo isotopes. Geochimica et Cosmochimica Acta 164, 1–16.
 Show in context
Show in context Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008; Wen et al., 2011; Xu et al., 2012; Chen et al., 2015; Kendall et al., 2015; Wen et al., 2015).
View in article
The last positive δ98Mo excursion is broadly correlated to the first appearance of trilobites in China, strong Mo enrichments and with the oxygenation event reported here (Dahl et al., 2010; Xu et al., 2012; Chen et al., 2015; Wen et al., 2015; Jin et al., 2016).
View in article
This prediction is in good agreement with the maximum values observed in the δ98Mo record during this time interval (Lehmann et al., 2007; Chen et al., 2015; Wen et al., 2015) (Fig. 2).
View in article
Weyer, S., Anbar, A.D., Gerdes, A., Gordon, G.W., Algeo, T.J., Boyle, E.A. (2008) Natural fractionation of 238U/235U. Geochimica et Cosmochimica Acta 72, 345–359.
 Show in context
Show in context This is possible due to the long residence time and uniform δ238U of uranium in the modern ocean and predicted for the Cambrian ocean (Weyer et al., 2008; Dahl et al., 2014; Tissot and Dauphas, 2015).
View in article
Wille, M., Nagler, T.F., Lehmann, B., Schroder, S., Kramers, J.D. (2008) Hydrogen sulphide release to surface waters at the Precambrian/Cambrian boundary. Nature 453, 767–769.
 Show in context
Show in context Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008; Wen et al., 2011; Xu et al., 2012; Chen et al., 2015; Kendall et al., 2015; Wen et al., 2015).
View in article
Xu, L., Lehmann, B., Mao, J., Nägler, T.F., Neubert, N., Böttcher, M.E., Escher, P. (2012) Mo isotope and trace element patterns of Lower Cambrian black shales in South China: Multi-proxy constraints on the paleoenvironment. Chemical Geology 318-319, 45–59.
 Show in context
Show in context Specifically, the molybdenum isotope (δ98Mo) record from shales and phosphorites show several fluctuations recorded in ~560 to 520 Myr old stratigraphic sections in China (Wille et al., 2008; Wen et al., 2011; Xu et al., 2012; Chen et al., 2015; Kendall et al., 2015; Wen et al., 2015).
View in article
The last positive δ98Mo excursion is broadly correlated to the first appearance of trilobites in China, strong Mo enrichments and with the oxygenation event reported here (Dahl et al., 2010; Xu et al., 2012; Chen et al., 2015; Wen et al., 2015; Jin et al., 2016).
View in article
Zhuravlev, A., Wood, R. (1996) Anoxia as the cause of the mid-Early Cambrian (Botomian) extinction event. Geology 24, 311–314.
 Show in context
Show in context Similar parallel positive carbon and sulphur isotope excursions during the late Cambrian SPICE event (Gill et al., 2011; Dahl et al., 2014) and the Botoman Sinsk event were interpreted to represent a period of enhanced organic carbon and pyrite burial (Zhuravlev and Wood, 1996).
View in article
top
Supplementary Information
S1. Methods, Samples and Geological Settings
Samples and geological settings
The material was obtained by AK during a field expedition in 1996 along the 1) Bolshaya-Kuonamka River (Anabar Uplift, Siberian Platform) (Kouchinsky et al., 2001) and 2) Malaya-Kuonamka River (Anabar Uplift) (Kouchinsky et al., 2001), and by Vladimir Pavlov and Vladimir Vodovozov in 2004 (Institute of Physics of the Earth, Moscow) from 3) Sukharikha River (Igarka region, western margin of the Siberian Platform) (Kouchinsky et al., 2007; see Fig. S-1). The stratigraphic sections at both localities consist of open-shelf marine facies (Rowland et al., 1998). The Tommotian-Atdabanian (Cambrian Stage 2–3 in Siberia) interval is found within in the Krasnoporog Formation (Rowland et al., 1998) and the Emyaksin (Kouchinsky et al., 2001) Formations at the Sukharikha River and the sections from the Anabar Uplift, respectively. The Krasnoporog Formation represents shallow shelf environments consisting primarily of burrow-mottled thick-bedded pink and grey lime mudstones with two archaeocyath-rich intervals at the base of the Atdabanian portion of the section (Rowland et al., 1998). The Emyaksin Formation dominantly consists of argillaceous lime mudstones, although the clay mineral content is low (<10 wt. %, Extended Data 1 and 2). The Emyaksin Formation belongs to the Yudoma-Olenek facies region (or belt) of the lower Cambrian deposits of the Siberian Platform (e.g., Varlamov et al., 2008 and references therein). A detailed interpretation of the depositional environments is provided for the analogous Erkeket and Medvezhya Formations of the northern part of the Yudoma-Olenek facies region (Kaufman and Knoll, 1995; Kaufman et al., 1996).
The sections are correlated to one another and to other sections globally via chemo- and biostratigraphy (Fig. S-2; Kouchinsky et al., 2012, 2015). Briefly, the Tommotian-Atdabanian is biostratigraphically defined by archaeocyaths located at 12–19 m above the base of the Krasnoporog Formation (Kouchinsky et al., 2012). This broadly coincides with where δ13C crosses 0 ‰ on the rising limb of the positive δ13C excursion (peak 'IV'). This δ13C excursion, which reaches +3 to +4 ‰ at its peak, is a globally recognised chemostratigraphic marker and as bracketed by 206Pb–238U zircon dates from two ash beds in Morocco (520.93 ± 0.14 Ma and 517 ± 1.5 Ma) (Maloof et al., 2010b). No erosional surface was revealed in the Krasnoporog Formation during field studies (Kouchinsky et al., 2007). At a constant sedimentation rate, we calculate the carbon isotope excursion (as defined by the two points where δ13C crosses 0 ‰) spans 1.3 ± 0.8 Myr. The δ34S and δ238U isotope excursions presented here both cover a similar time span. Profallotaspis jakutensis, one of earliest trilobites, occurs ~10 metres above the point where the δ13C crosses -0.5 ‰ on the rising limb of the carbon isotope excursion at Zhurinskii Mys, Lena River (Rozanov et al., 2008).
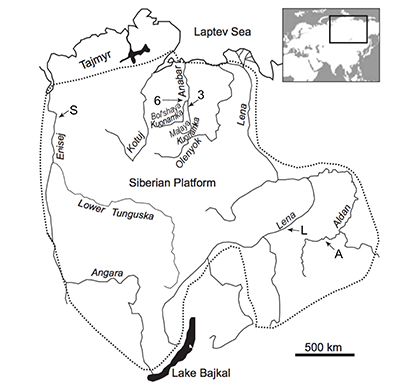
Figure S-1 Location of the studied sections Sukharikha (S), Bolshaya Kuonamka (6) and Malaya Kuonamka (3) and other sections at the Siberian platform discussed in the text (L–Middle Lena, A–Aldan Rivers).
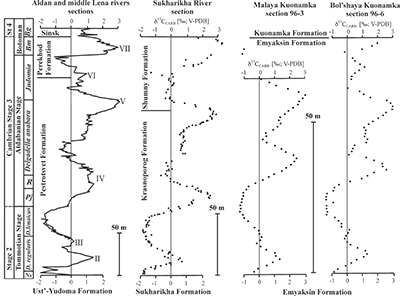
Figure S-2 Carbon isotope stratigraphy of the three studied sections and composite curve from Aldan and Middle Lena Rivers (Brasier et al., 1994; Kouchinsky et al., 2007). Zones as defined in the Lena-Aldan area: Ns – Nochoroicyathus sunnaginicus; D. regularis – Dokidocyathus regularis; D. lenaicus – Dokidocyathus lenaicus–Tumuliolynthus primigenius; Pj – Profallotaspis jakutensis; R – Repinaella; Bm – Bergeroniellus micmacciformis; Bg – Bergeroniellus gurarii.
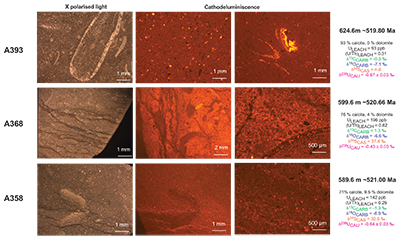
Figure S-3 Photomicrographs of samples (A358, A368 and A393) from the Sukharikha River section show microstructure and cathodoluminescent (CL) characteristics. Recrystallised shell fragments are embedded in a micrite matrix. Photographs are taken from thin section using multi-composite exposure (HDR). Selected geochemical data are summarised; n.d. – no data.
Methods
δ238UCAU. We calibrated (see Supplementary Information) and utilised a soft leaching procedure to extract mainly carbonate-associated U (CAU) from our samples and to avoid U associated with authigenic carbonate fluorapatite and ferric oxyhydroxide-associated P (Jeppsson et al., 1999), or any detrital or organic-bound U. Samples were cut in ~10–20 g pieces and secondary veins, if present, were removed using a water-cooled saw. The rock surface was first leached in 10 % acetic acid to remove surface contaminants, dried and then crushed in a shatter box to a fine powder. For analysis of carbonate-associated uranium, approximately 1–3 g of the fine powder were weighed out in 50 mL centrifuge tubes and leached using a mild leaching procedure: 40 mL 10 % acetic acid were added 10 mL at a time to dissolve the carbonate preferentially. All labware in contact with dissolved sample material were acid-cleaned in the same acid prior to use. The mixture was shaken several times and left overnight at 50 °C in a warm bath, then ultrasonicated and centrifuged for 5 min at 2500 rpm before the supernatant was taken up by syringe and filtered through 0.22 µm filter to separate the liquid from the solids. Following the removal of the supernatant, the residue was washed with 5 mL 10 % acetic acid, centrifuged before the supernatant was again transferred to the leachate to ensure maximum transfer of the carbonate-associated uranium. Still, calcite is not quantitatively extracted from our sample powders. Extraction yields were 57 ± 19 % as calculated from the bulk calcite contents (83 ± 9 wt. % CaCO3; Extended Data 2) and the Ca concentration in the leachates (19 ± 4 wt. % Ca).
U and Th concentrations were measured in a small fraction (~1 %) of the leachate on a Thermo X-Series 2, quadrupole inductively coupled mass spectrometer (q-ICPMS). U isotope analyses were performed on the remaining fraction (~99 %) or a smaller aliquot with 60–600 ng U. The leachate was transferred to 60 mL Teflon beakers dried down on a hot plate and redissolved in 7 N nitric acid in a 16 mL Teflon beaker. Samples were spiked prior to chemical purification using the IRMM-3636 233U–236U double spike (Condon et al., 2010) and left for >48 hours on a hotplate first in hydrochloric acid and later in nitric acid. This allowed the U from the spike to equilibrate isotopically with U in the sample and ensure all U compounds were in the same chemical form prior to ion chromatographic separation. Chemical purification of U and its isotopic analysis were conducted following the procedures outlined in Connelly et al. (2012) using a Neptune Plus Multi-Collector ICPMS. The spike/sample ratio was kept constant for all samples and standards during each analytical session. We estimate the long-term reproducibility and accuracy of our 238U/235U data to be ±0.03 ‰ (2SD). For example, BCR-2 (whole rock) and IAPSO seawater are found to be δ238U = –0.271 ± 0.017 ‰ and –0.372 ± 0.022 ‰ (2SE, n =5), respectively.
δ34SCAS. The sulphur isotope composition of carbonate-associated sulphate (CAS) was obtained using a traditional approach (Wotte et al., 2012). In summary, 3–8 g of the fine sample powder were treated with a NaCl solution, followed by several distilled water rinses to remove any soluble sulphates that might have been present in the samples. The samples were then dissolved using 4 N HCl. The leachates were centrifuged and vacuum filtered (45 µm) to remove any insoluble portion of the sample, before ~100 mL saturated BaCl2 solution were added to allow sulphate to precipitate as BaSO4 from the solution. We let samples sit for at least three days to ensure complete precipitation. The BaSO4 was separated from the remaining solution via filtration and allowed to dry. The 34S/32S isotope ratios were analysed through on-line combustion using an Elementar Isotope Cube elemental analyser coupled to Isoprime 100 continuous-flow stable isotope ratio mass spectrometer at the Virginia Polytechnic Institute and State University. Samples are reported in standard delta notation (δ34S) as per mille deviations from Vienna Canon Diablo Trolite (VCDT) and were calibrated to this scale with international isotope standards NBS-127, IAEA SO-5 and IAEA SO-6. Long-term reproducibility of the δ34S measurement to be <0.2 ‰ (1 SD) through replicates of international isotope standards listed above. We estimate the external reproducibility of our δ34S data to be better than 1 ‰ based on with replicate dissolutions of two samples (DM4-12, DM4-36).
S2. Additional Geochemical and Mineralogical Characterisation
The concentration of Mg, Al, Fe and Ca in the samples was measured in the same diluted acetic leachates that carbonate-associated uranium was obtained (Extended Data 1). The low Mg, Al and Fe concentration relative to Ca indicates that dolomite and clay are not dissolved. This is fully consistent with mineralogical characterisations showing that samples contain mostly calcite and only subordinate proportions of other mineral phases, i.e. <5 wt. % clay and dolomite (Extended Data 2).
The total organic carbon (TOC) content was measured from the residue after the 4 N HCl leach in CAS extractions using an FLASH 2000 element analyser coupled to Thermo Finnigan Delta V Plus continuous-flow mass spectrometer. All samples contain low TOC (<0.16 wt. %, median 0.03 wt. %) (Extended Data 3).
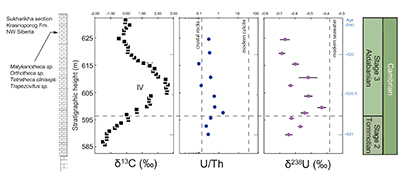
Figure S-4 Geochemical profiles from the Sukharikha River section showing δ13C, U/Th (note the logarithmic scale) and δ238U in stratigraphic context. The lithostratigraphy is adapted from Kouchinsky et al. (2007) and Rowland et al. (1998). The age assignment follows the model proposed by Maloof et al. (2010) assuming synchronicity worldwide in δ13C record tied to five absolute U/Pb age dates obtained from interbedded volcanic ashes in sections from Morocco (Maloof et al., 2010a). The uncertainty on δ13C is smaller than symbol size (2 SD reproducibility of samples from the same bed). The uncertainty of U/Th is <30 % measured on replicate leachates (see Extended Data 1). The uncertainty of δ238U is shown with error bars as 2 SE (replicate analyses of the same sample solution, see Table S-1).
Correlations
There is no systematic correlation between the δ238U excursion and geochemical indicators for dolomitisation, pore water redox conditions, detrital input and primary carbonate mineralogy (Fig. S-5, Table S-1). There is, however, a good correlation between δ238U and δ13C (R = 0.82, p = 0.005, Table S-1).

Figure S-5 Comparison of δ238U and highly reactive U to δ13C and geochemical indicators of dolomitisation (Mg/Ca, dolomite), pore water redox conditions (TOC), diagenetic alteration (Mn/Sr, δ18O), detrital input (Al/Ca, clay content), and primary carbonate mineralogy (Sr/Ca).
Table S-1 Pearson's correlation coefficients and p-values calculated to test the influence of diagenetic indicators on δ238U and U/Th. Uranium content (U) is linearly correlated to U/Th, hence the significance of the correlations between U and diagenetic indicators are similar. Statistical significant relationships are in bold (confidence interval = 5 %).
| R | p-value | |
| δ238U vs. U | 0.12 | 0.71 |
| δ238U vs. U/Th | 0.15 | 0.67 |
| U vs. U/Th | 0.96 | 8.11E-07 |
| δ238U vs. δ13C | 0.82 | 0.005 |
| δ238U vs. Mg/Ca | 0.52 | 0.15 |
| δ238U vs. TOC | -0.31 | 0.41 |
| δ238U vs. δ18O | 0.68 | 0.04 |
| δ238U vs. Mn/Sr | 0.14 | 0.69 |
| δ238U vs. Al/Ca | #N/D | #N/D |
| δ238U vs. Sr/Ca | 0.5 | 0.14 |
| δ238U vs. calcite | -0.66 | 0.07 |
| δ238U vs. quartz | 0.69 | 0.05 |
| δ238U vs. dolomite | 0.38 | 0.34 |
| δ238U vs. ankerite | -0.68 | 0.16 |
| δ238U vs. chlorite | 0.14 | 0.76 |
| δ238U vs. mica | 0.21 | 0.61 |
| δ238U vs. K-feldspar | 0.44 | 0.27 |
| U/Th vs. δ13C | 0.15 | 0.67 |
| U/Th vs. Mg/Ca | 0.49 | 0.15 |
| U/Th vs. TOC | -0.1 | 0.78 |
| U/Th vs. δ18O | 0.59 | 0.07 |
| U/Th vs. Mn/Sr | -0.13 | 0.71 |
| U/Th vs. Al/Ca | #N/D | #N/D |
| U/Th vs. Sr/Ca | 0.16 | 0.65 |
| U/Th vs. calcite | -0.13 | 0.75 |
| U/Th vs. quartz | 0.04 | 0.92 |
| U/Th vs. dolomite | 0.3 | 0.44 |
| U/Th vs. ankerite | -0.24 | 0.63 |
| U/Th vs. chlorite | 0.01 | 0.98 |
| U/Th vs. mica | -0.13 | 0.73 |
| U/Th vs. K-feldspar | 0.06 | 0.88 |
S3. Methods - Calibration of the CAU Extraction Procedure
The extraction of carbonate-associated uranium was calibrated using a four-step sequential leaching procedure. The extraction procedure is designed to minimise extraction of uranium associated with carbonate fluoroapatite, ferric oxyhydroxide-associated P, silicates and organic-bound U, while maximising the yield of calcium carbonate-associated uranium. Phosphate minerals resist dissolution in mild acetic acid at pH > 3.6, where limestone dissolves (Jeppsson et al., 1999). Silicate-bound U and organic-bound U dissolve in hydrofluoric acid and nitric acid, respectively. Existing extraction procedures utilise 0.5 M HCl leaching instead of acetic, so we explored the following leaching procedure:
Sequential extraction
Step 1: 1.7 M (10 %) acetic acid (pH > 3.6, T = 50 °C, overnight)
Step 2: 0.5 M HCl (T = 50 °C, overnight)
Step 3: 2 M HCl (T = 50 °C, overnight)
Step 4: 28 M HF + 7 M HNO3 (T = 50 °C, overnight)
The U distribution in two end-member reference samples with variable phosphate contents were compared, including a chalk (~100 % CaCO3, 0 wt. % P2O5) from the Cretaceous–Paleogene boundary at Stevns, Denmark, and phosphoritic sedimentary rock (8.5 wt. % P2O5) from the Middle Cambrian Alum Shale formation, Sweden.
The samples were crushed to fine powders and analysed in duplicates. The U concentration in the leachates was measured using ICP-MS. Error bars represent 1 SD of replicate analyses.
Table S-2 Uranium extracted from two reference materials with the sequential extraction procedure.
| U (ppb) | KTChalk | MCPhos |
| (100 % CaCO3) | (8.5 wt. % P2O5) | |
| 10 % acetic acid | 70 ± 4 | 440 ± 5 |
| 0.5 M HCl | 19 ± 1 | 872 ± 423 |
| 2 M HCl | 4 ± 0 | 133 ± 49 |
| HF + HNO3 | 14 ± 0 | 994 ± 8 |
| Total | 107 ± 4 | 2439 ± 426 |
Most of the U in the chalk sits in the acetic acid extractable fraction, whereas the majority of U in the phosphorite-containing sediment sits in the HCl extractable fraction and HF–HNO3 extractable portions. This result is expected since the U content in phosphate minerals is substantially higher (10–100 ppm) in the phosphate minerals than in the limestone (0.1–1 ppm).
The relative U proportions extracted with acetic and hydrochloric acid are shown in Table S-3 below.
Table S-3 Comparison of extraction yields for acetic acid vs. hydrochloric acid of various molarity.
| U | KTChalk | MCPhos |
| 10 % acetic acid | 75 ± 4 % | 30 ± 0 % |
| 0.5 M HCl | 20 ± 1 % | 60 ± 29 % |
| 2 M HCl | 4 ± 0 % | 9 ± 3 % |
| Total | 100 % | 100 % |
We favour an extraction based on mild acetic acid, since a substantial portion of phosphorite-bound U is extracted with 0.5 M HCl and it only comes with a loss of ~20 % of the remaining CAU.
Reproducibility
Repeated leaching experiments with acetic acid were performed with three natural limestone samples. Importantly, our acetic acid leaching procedure always yields the same d238U values even though the extraction yield sometimes varies. Therefore, we can conclude that the leaching procedure does not induce any isotope offset.
Table S-4 Repeated analyses of carbonate-associated U and δ238UCAU using the mild acetic acid extraction (with variable reaction time).
| Replicate | Reaction time | U (ppb) | δ238U (‰) |
| SRM-1d (modern argillaceous limestone) | |||
| #1 | 16 hr | 70 | –0.09 ± 0.02 |
| #2 | 16 hr | 743 | –0.08 ± 0.02 |
| #3 | 16 hr | 639 | –0.11 ± 0.02 |
| T1-13 (Cambrian limestone) | |||
| #3 | 30 min | 298 | –0.85 ± 0.02 |
| #4 | 4 hr | 292 | –0.83 ± 0.02 |
| #5 | 16 hr | 281 | –0.82 ± 0.03 |
| T1-26.5 (Cambrian limestone) | |||
| #1 | 16 hr | 102 | not determined |
| #2 | 16 hr | 155 | –0.56 ± 0.02 |
| #3 | 16 hr | 154 | –0.60 ± 0.03 |
Low extraction yields when carbonate grains are protected
To explore the nature of variable extraction yields, we mixed KT chalk and MCPhos in distinct proportions to see if the presence of acid-resistable phases would protect carbonate grains from dissolving. Indeed, we observe that the extraction yields in the acetic fraction are systematically lower than predicted (35 % vs. 40 % in a 1:1 mixture and 24 % vs. 33 % in a 1:2 mixture) in the presence of MCPhos. Accordingly, a systematically higher yield was observed in the subsequent HCl extractable fraction (37 % vs. 27 % in a 1:1 mixture and 34 % vs. 30 % in a 1:2 mixture). Hence, we infer that acetic acid-resistant phases protected carbonate grains against dissolution. By implication, a similar phenomenon may explain the variable extraction yields observed in the repeated analyses of some samples (e.g., SRM-1d #1), if the sample powder is not fully mixed with the acid. Therefore, acid and sample powders are now carefully shaken during the extraction. In any case, the protection of carbonate grains does not induce any isotope fractionation.
Table S-5 Extraction yields for various mixtures of KTChalk and MCPhos.
| Acid | Chalk | 1:1† | 1:2ß | MCPhos | 1:1† | 1:2ß |
| measured | predicted | |||||
| 10 % acetic | 65 % | 35 % | 24 % | 18 % | 40 % | 33 % |
| 0.5 M HCl | 18 % | 37 % | 34 % | 36 % | 27 % | 30 % |
| 2 M HCl | 4 % | 5 % | 12 % | 5 % | 5 % | 5 % |
| HF + HNO3 | 13 % | 24 % | 3 % | 41 % | 28 % | 33 % |
†Mixing ratio 1:1 corresponds to 1.0187 g KTChalk (108 ng U) + 0.0519 g MCPhos (127 ng U).
ßMixing ratio 1:2 corresponds to 1.0993 g KTChalk (117 ng U) + 0.1138 g MCPhos (278 ng U).
S4. Marine Molybdenum and Uranium Cycle Box Model
Uranium
A mass balance budget for the oceanic uranium cycle must include all the major sources and sinks (Tissot and Dauphas, 2015). The dominant U input to the oceans (JIN) is via rivers. The sink fluxes (JOUT) can be divided into two groups – a) sediments deposited under anoxic waters (JANOX) with large isotopic difference (ΔANOX ~ 0.50 ‰) and b) sediments deposited in other settings (JOTHER) under oxygenated waters with less isotopic difference (ΔOTHER ~ <0.10 ‰) relative to overlying seawater. At steady state, the following mass balance equations must apply:
Elemental mass balance at steady state:
Eq. S-1
JIN = JOUT
where
Eq. S-2
JOUT = JANOX + JOTHER
Isotopic mass balance at steady state can be written as:
Eq. S-3
δIN * JIN = δOUT * JOUT
The majority of oceanic U enters via rivers (≥80 %) and groundwater (≤20 %) (Dunk et al., 2002; Tissot and Dauphas, 2015). The weighted average riverine input carries uranium with δ238U = –0.34 ‰ (Andersen et al., 2016). However, two analyses from the Yangtze River (-0.72 and -0.68 ‰), which has a large discharge, significantly shift this average to a lower value. The reason for the low value is not known, and anthropogenic contamination does not appear to be the cause (e.g., phosphate fertiliser; Andersen et al., 2016). Previous global riverine estimates yielded –0.30 ‰ to –0.27 ‰ (Noordmann et al., 2016). Regardless, it appears that the riverine composition is indistinguishable from average continental crust at –0.30 ± 0.04 ‰ and –0.31 ± 0.05 ‰ (2 SE) (Noordmann et al., 2016). We adopt a value of –0.27 ‰, but also explore a range of values, which are listed in Table S-6.
Eq. S-4
δOUTJOUT = δANOXJANOX + δOTHERJOTHER
We define the fraction of total sedimentary U burial occurring in anoxic settings as:
Eq. S-5
ƒU = JANOX/JOUT
Therefore, the isotope mass balance equation can be written as:
Eq. S-6
δOUT = δANOXƒU + δOTHER (1 − ƒU)
The isotope composition of each sink, i, (δi) relates to the isotope composition of contemporaneous seawater (δSW) via the average isotopic difference (Δi) expressed during sediment burial in each sink:
Eq. S-7
δANOX = δSW + ΔANOX
Eq. S-8
δOTHER = δSW + ΔOTHER
Therefore, the isotope mass balance equation (Eq. S-6) relates the isotope composition of seawater to the fraction of anoxic U burial (fU) assuming the other parameters are constant through time (δIN, ΔANOX, ΔOTHER).
Eq. S-9
δIN = δSW + ΔOTHER + (ΔANOX − ΔOTHER) * ƒU
Eq. S-9 tells us that the U isotope composition of seawater at steady state is offset from input composition by the magnitude of the isotopic difference in other settings (ΔOTHER) - and decreases by the magnitude of (ΔANOX - ΔOX) as the proportion U burial into anoxic settings increases from 0 to 100 %:
Eq. S-9, rearranged
δSW = δIN − ΔOTHER − (ΔANOX − ΔOTHER) * ƒU
All model parameters carry considerable uncertainty due to limited number of representative isotope analyses for each flux and uncertainty in the magnitude of the burial fluxes associated with each isotopically distinct pathway. However, all parameterisations consistently demonstrate a negative relationship between δSW and fU (Fig. S-6).
Table S-6 Five parameterisations for the modern oceanic uranium isotope budget shown in Figure S-6. The models are broadly consistent with the modern ocean state.
| Case | 1 | 2 | 3 | 4 | 5 | 6 |
| Default | low δIN | hi ΔANOX | hi δIN | low ΔANOX | hi ΔOTHER | |
| δIN | –0.27 ‰ | –0.34 ‰ | –0.27 ‰ | –0.30 ‰ | –0.27 ‰ | –0.27 ‰ |
| ΔOTHER | 0.04 ‰ | 0.00 ‰ | 0.10 ‰ | 0.10 ‰ | 0.04 ‰ | 0.15 ‰ |
| ΔANOX | 0.50 ‰ | 0.50 ‰ | 0.60 ‰ | 0.60 ‰ | 0.40 ‰ | 0.40 ‰ |
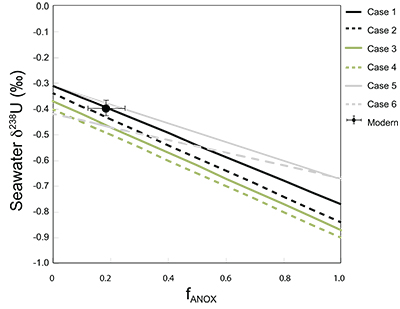
Figure S-6 Relationships between δSW and anoxic U burial fraction (fU) in the ocean are shown when the system is at steady state. The fraction of total oceanic U burial in anoxic basins (fU) is a key parameter that can shift seawater δ238U significantly below the modern value (black circle). The remaining U burial occurs in various oxygenated settings with a smaller isotopic imprint on global seawater (see text for details).
Sensitivity analyses
The U isotope composition of seawater is particularly sensitive to U burial in anoxic settings due to the large U isotopic difference when sediment is buried in these settings: ΔANOX is 0.4–0.6 ‰ (Romaniello, 2012; Andersen et al., 2014; Noordmann et al., 2016).
The Jother flux incorporates U removal via reducing sediments, hydrothermal alteration and biogenic carbonate and silica. The modelled isotopic difference from seawater in these settings, ΔOTHER, represents a weighted average of these burial fluxes.
Eq. S-10
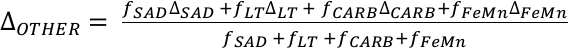
Here, the fraction of total U burial in various settings (i) is denoted fi and the associated isotopic difference from open-ocean seawater is Δi. Here, SAD stands for Sulphidic At Depth and includes both siliciclastic and carbonate sediments overlain by a fully oxic water column, but with hydrogen sulphide accumulating in pore waters of the sediment. Reductive U removal induces an U isotopic difference from seawater similar to both reducing siliciclastic (0.04 to 0.29 ‰) and carbonate sediments (0.2–0.4 ‰) that are deposited in high-productivity oxic settings (Noordmann et al., 2016). A similar isotopic difference (0.0–0.2 ‰) is also observed during low temperature basaltic alteration (Andersen et al., 2015), which has been estimated to account for 24 ± 12 % of total U removal from the oceans today (Dunk et al., 2002; Noordmann et al., 2016). These isotopic differences are small, but distinctly higher than those produced during carbonate precipitation in oxygenated environments with negligible isotopic difference (0.0 ± 0.1 ‰; Chen et al., 2016), and during removal with metalliferous oxides in the deep ocean (fFeMn = 7 ± 5 %), which induces an isotopic offset in the opposite direction (–0.24 ‰; Noordmann et al., 2016).
A sensitivity analysis of Eq. S-10 using the above average values and uncertainty estimates for fi and Δi yields a small value for ΔOTHER = 0.09 ± 0.08 ‰. This value is indistinguishable from the value, ΔOTHER = –0.02 ± 0.05 ‰, obtained from Eq. S-9 for the modern oceans at steady state with respect to input and anoxic burial fraction (δIN = 0.285 ± 0.015 ‰, δSW = 0.39 ± 0.01 ‰ and fANOX = 12–25 %). Uncertainty estimates represent propagated errors in Eqs. S-9 and S-10. The anoxic burial fraction is calculated using these values and uncertainties for ΔANOX, and δIN and ΔOTHER = –0.02 ± 0.05 ‰.
The marine Mo budget can be written in terms of its major sources (rivers, >90 %) and three major sinks: a) euxinic sediments (here denoted anoxic), b) high-productivity oxic sediments that are sulphidic at depth (SAD), and c) oxygenated sediments containing ferromanganese oxides (OX), each of which has increasing isotope fractionation from seawater. The equations for the marine Mo cycle at steady state are derived in Dahl et al. (2011). Briefly, the elemental mass balance for the ocean implies that the input flux (JIN) matches the total output flux (JOUT):
Eq. S-11
JIN = JOUT
where the output flux consists of the three major sinks:
Isotope mass balance can be written as in Eq. S-3. Most Mo enters the ocean via rivers (~ 95 %; Miller et al., 2011). The weighted average riverine input carries molybdenum with δ98Mo = 0.7 ‰ based on analyses of waters representing 22 % of global riverine discharge (Archer and Vance, 2008).
The isotope composition of the oceanic output is given by the isotope composition (δi) of the major sinks weighted according to the burial fraction of each sink (fi = Ji/JOUT). Here, we use fMo for the Mo burial fraction in anoxic settings.
Eq. S-12
δOUT = δANOXƒMo + δSADƒSAD + δOXƒOX
The magnitude of the isotopic difference associated with burial in each sink is here defined as a positive number (Δi = δSW - δi ), which increases from anoxic (euxinic) to oxic environments ( ΔOX > ΔSAD > ΔEUX). Eqs. S-3 and S-12 combine to:
Eq. S-13
δSW = δIN + (1 − ƒMo)ΔOX − ƒSAD(ΔOX − ΔSAD)
Eq. S-13 states that seawater δ98Mo will always be positively offset from riverine input. The maximum value of 3.5 ‰ (δIN + ΔOX = 3.5 ‰) will be found in a fully oxygenated ocean, and a minimum value of 0.7 ‰ occurs in a fully anoxic (euxinic) ocean (in both cases, fSAD = 0).
The combined Mo and U box model for the ocean
The anoxic burial fluxes of Mo and U are correlated, and the total anoxic burial fractions (fU, fMo) yield 0 and 1 when all sediment burial occurs in oxic and anoxic (euxinic) settings, respectively. Hence, the correlation may be described by a power law with exponent a.
Eq. S-14
ƒMo = ƒαU
We constrain the value of a from the anoxic burial fraction obtained in the marine budget of the modern Mo and U cycles. Published estimates are fMo = 0.06–0.15 (Scott et al., 2008; Kendall et al., 2009) and fU = 0.12–0.25 (Morford and Emerson, 1999; Dunk et al., 2002), so that a = ln(fMo)/log(fU) = 1.34 ± 0.38 (errors propagated assuming parameter estimates are uncorrelated). Three examples of the functional relationships between the anoxic Mo and U burial fractions are shown in Figure S-7 and the consequences for seawater composition is shown in Figure S-8.
With parameter values listed in Table S-7, our calculations can simultaneously fit modern and Cambrian ocean δ238U and δ98Mo constraints. We note that a = 1.15–1.24 best fits simultaneously the two ocean states, favouring the higher estimates for the modern anoxic Mo burial fraction (fMo = 0.12–0.14, if fU = 0.18 today).
Table S-7 Parameter values used in the coupled Mo–U isotope mass balance models for today's ocean.
| Mo | U | |
| δIN | 0.7 | -0.27 |
| ΔOX | 2.8 | 0.04 |
| ΔANOX | 0.0 | 0.50 |
| ΔSAD | 1.4 | - |
| ƒOX | 30 % | 82 % |
| ƒSAD | 58 % | - |
| ƒEUX | 12 % | 18 % |
| Predicted δSW | 2.35 | -0.393 |
| Observed δSW | 2.34 ± 0.10 | -0.392 ± 0.005 |
(Note that all Δs are here defined positive, despite Mo and U isotope fractionations have opposite signs).
Download in Excel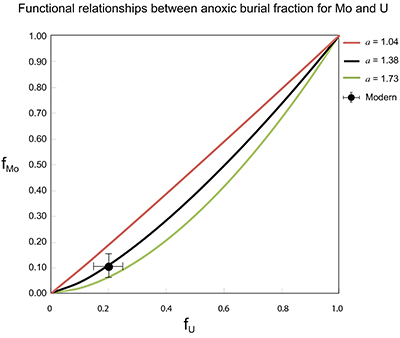
Figure S-7 Modelled functional relationships between euxinic Mo and U sinks. Modern estimates for the anoxic burial fractions (white square) suggest a is slightly larger than 1, consistent with modern oceanic budgets (Noordmann et al., 2016) where a = 1.38 ± 0.34.
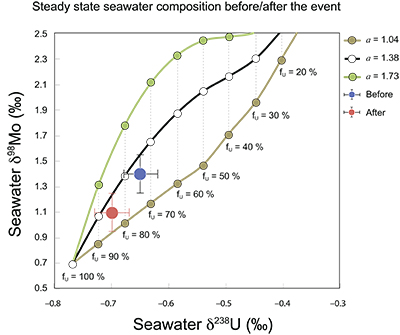
Figure S-8 Modelled seawater composition (δ238U, δ98Mo) for the early Cambrian steady states before and after the Cambrian Stage 2–3 event. The left most point represents 100 % burial in anoxic settings (fU = fMo = 1). At each step point towards the right, fU decreases 10 % (i.e. 90 %, 80 %, 70 %, etc.). The estimated composition of the δ238U and δ98Mo of early Cambrian seawater in ‰ before and after the event are (-0.65, -0.70) and (1.4, 1.1), respectively, Error bars show ±0.03 ‰ and ±0.15 for δ238U and δ98Mo, respectively.
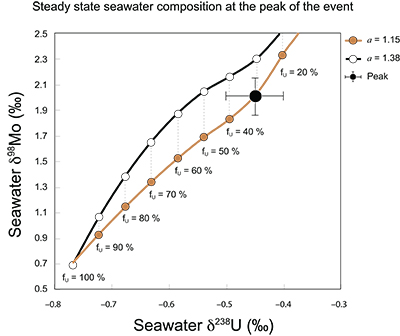
Figure S-9 The predicted composition of seawater at steady state for a = 1.15–1.38 is consistent with observations at the peak of the oxygenation event (δ238U = –0.45 ‰, δ98Mo = 2.0 ‰) with only 30 ± 10 % U removal into anoxic settings (corresponding to 25 ± 10 % and 19 ± 8 % Mo removal for a = 1.15 and 1.38, respectively).
S5. Marine Carbon and Sulphur Cycle Box Model
We present a simple model to quantify the organic carbon loading onto the seafloor and its influence on seawater δ13C and δ34S.
The isotopic and elemental mass balance equations for carbon and sulphur in a 1-box ocean is given as a function of time by the long-term imbalance between sources and sinks (Eqs. 3a and 3b in Kurtz, 2003). The δ13C of seawater (δC) is a function of the global oceanic C inventory (M), oceanic C input flux (JIN) and its isotope composition (δC, IN) as well as the organic proportion of total marine C burial (fORG) and average isotopic difference (ΔBIO) between δ13C of buried organic matter and seawater.
Eq. S-15
δC = δC,IN − M/JIN * d(δC)/dt + ƒORG * ΔBIO
The equation reduces to the steady state equation at times when the δ13C of seawater is not changing in time: d(δC)/dt = 0.
Table S-8 Parameter values used for the C and S modelling.
| Modern alue | Explored range | Explanation | Ref | |
| α | 0.0072 | x (3-30) | Ratio of pyrite formation to organic carbon remineralisation rate | B07 |
| JRAIN | 192 · 1012 | ¥ | mol/yr. Modern organic rain rate | |
| JORG | 26 · 1012 | ¥ | mol/yr. Modern marine organic C burial rate | B07 |
| JLAND | 26 · 1012 | ß | mol/yr. Modern terrestrial organic C burial rate | |
| JEVAP | 2.1·1012 | x (0.2 - 1) | mol/yr. Cenozoic sulphate burial rate | CF09† |
| JCARB | 216·1012 | x (0.2 - 1) | mol/yr. Modern carbonate burial rate | BB12 |
| δIN.C | –5 ‰ | –5 ± 1 ‰ | δ13C of oceanic input | |
| ΔC | 26 ‰ | 24-30 ‰ | Average δ13C offset between seawater and buried organic matter | |
| δin.S | 8 ‰ | 4-16 ‰ | δ34S of oceanic input | |
| ΔS | 35 ‰ | 35-50 ‰ | Average δ34S offset between seawater and buried pyrite | |
| SR | 40 · 1012 | mol/yr. Modern organic burial rate | B07 | |
| SO42- | 28 | 2-3 | mM. Modern oceanic sulphate level | |
| JPY | 1.2 · 1012 | ¥ | mol/yr. Modern pyrite burial rate | B07 |
† The size of the modern oxidising C and S sinks were established from the isotope-derived f-constraints (Burdige, 2007; Saltzman and Thomas, 2012), suggesting ƒORG = 0.192 and ƒPY = 0.36 leads to steady state seawater values of δ13C = 0 ‰ and δ34S = 21 ‰, respectively. We assume that the modern terrestrial organic carbon burial equals that of marine organic carbon burial (Bergman et al., 2004), and neglect terrestrial pyrite burial.
¥ Model results are given in Tables S-9 to S-14
ß Terrestrial organic carbon burial (e.g., coal) is assumed equal to marine organic carbon (Bergman et al., 2004). Ref. B07 = Burdige (2007), Ref CF09 = Canfield and Farquhar (2009), Ref BB12 = Berner and Berner (2012).
Eq. S-16
δC = δC,IN + ƒORG * ΔBIO
The C and S cycles are instantaneously at steady state before the isotope excursion, at the peak of the isotope excursion, and after the isotope excursion, when d(δC)/dt = 0 and d(δS)/dt = 0. In the following, we use the constraints on fORG and fPY at these time points to explore how enhanced organic carbon loading on the seafloor could have simultaneously affected the marine C and S cycles.
Carbon isotopes
The C isotope composition of seawater is a function of the fraction of marine organic carbon burial to total C burial (fORG = JORG / [JCARB + JORG]), where the remainder C is buried as marine carbonate with same isotope composition as average seawater.
Eq. S-17
ƒORG = JORG / (JCARB + JORG)
For example, assuming modern values for δin and ΔC (Table S-8) a change in seawater δ13C from 0 to 3 ‰ implies that fORG increases from 19 % to 31 % (+60 % relative increase).
Marine organic carbon burial is related to organic carbon rain rate measured at the seafloor (JRAIN) and the fraction of this organic carbon that is remineralised inside the sediments (fREMIN):
Eq. S-18
JORG = JRAIN * (1 - ƒREMIN)
Although, global estimates for organic burial rates vary by more than an order of magnitude (13-217 · 1012 mol/yr), Burdige (2007) revised these estimates and provided a best estimate of JORG = 26 · 1012 mol/yr and depth-integrated rates of organic carbon remineralisation (= fREMIN · JORG) accounted for 166 · 1012 mol/yr. Thus, the total organic load on ocean sediments and corresponding weighted average of the remineralisation fraction are JRAIN = 192 · 1012 mol/yr and fREMIN = 87 % (Burdige, 2007), respectively. The average burial efficiency (BE = 1-fREMIN = 13 %) mainly reflects shallow settings with high sedimentation rates where the burial efficiency can be up to 30 % in muddy sediments and only 1 % in sandy sediments (Burdige, 2007).
The fraction of organic carbon that is remineralised in sediments varies as a function of the quality of organic matter. With faster sinking rates for marine organic matter, we expect a higher labile fraction to be delivered to the sediments. Therefore, we also expect less remineralisation inside the sediments, fREMIN <87 %, prior to the Cambrian Stage 2–3 oxygenation episode, when organic particles were smaller and the overall quality of organic matter delivered to the seafloor was lower. We derive the range of possible values for fREMIN consistent with the carbon and sulphur isotope data.
Sulphur isotopes
The stable isotope composition of sulphur in the oceanic sulphate pool (δ34S, here abbreviated δS) is at quasi-steady state and is related to the ratio of global pyrite to total sulphur burial in the oceans (fPY), the average isotopic difference between seawater and buried pyrite (ΔPY), and the isotope composition of the inputs (δS,IN):
Eq. S-19
δS = δS,IN + ƒPY * ΔPY
In the sulphur cycle, the major sinks are pyrite burial (JPY) and carbonate plus evaporate deposition (JEVAP) with the latter displaying same S isotope composition as average seawater.
Eq. S-20
ƒPY = JPY / (JPY + JEVAP)
For example, the observed change in seawater δ34S from 28 to 40 ‰ during the Cambrian Stage 2–3 oxygenation episode suggests fPY increases from 40 % to 70 % (+~75 % relative increase) if we assume δS,in and ΔPY were constant and at modern values (Table S-8).
Table S-9 Changes in the f-ratios during the Cambrian Stage 2–3 oxygenation episode. Uncertainties are propagated from the uncertainty of the isotope compositions of the inputs and the isotope fractionation associated with burial in reducing sinks (Table S-8)
| Before the event | At the peak | Behaviour | Modern value | |
| δC | 0 % | 3 % | increase | 0 ‰ |
| δS | 28 % | 40 % | increase | 21 ‰ |
| this leads to: | ||||
| ƒORG | 17 ± 4 % | 28 ± 5 % | increase | 20 ‰ |
| ƒPY | 40 ± 17 % | 70 ± 22 % | increase | 36 ‰ |
Relationship between organic carbon loading and seawater δ13C and δ34S
Enhanced organic carbon export to the seafloor will promote both marine organic carbon burial and pyrite burial. Below we explore the solution space consistent with the isotope trajectories during the Cambrian Stage 2–3 oxygenation event.
Pyrite burial is a function of the remineralised fraction of the organic carbon supplied to the sediments (e.g., JRAIN·fREMIN):
Eq. S-21
JPY = α * JRAIN * ƒREMIN
Here, a constant value α = 0.0072 can be derived empirically from the modern-day global ocean state (using parameter values listed in Table S-8). The α value is determined by numerous physical and chemical parameters. We assume that the sulphate reducing microorganisms account for a constant fraction of anaerobic remineralisation of organic carbon and that the stoichiometric factors relating reactive sulphur species produced (∑S2- and S0) per C respired, as well as FeS2 trapped per reactive S produced, are constant. The ratio between sulphide trapped as pyrite and total sulphide produced (β) will, however, change as a function of the degree of sediment mixing by bioturbation (Canfield and Farquhar, 2009).
Generally, the value of α need not have remained constant over Earth history, since both sediment mixing by bioturbation and oxygen availability in sediments have certainly changed over time. Cambrian oxygen levels were lower and bioturbation was less widespread and less efficient than today (this work; Mangano and Buatois, 2014; Tarhan and Droser, 2014). Therefore, we expect higher reactive Fe availability in more anoxic oceans, less sulphide oxidation in sediments and more pyrite sulphur to be trapped per organic carbon loaded into the sediment. This would increase the value of α, so that α > 0.007. Conversely, lower marine sulphate levels might decrease α if anaerobic processes other than sulphate reduction contributed to a larger part of the remineralisation. Canfield and Farquhar (2009) estimated the change of β in response to the onset of bioturbation. They found that a decrease of β from 0.22–1.00 to 0.033 would lead to a –30 ‰ drop of δ34S by ‘turning on’ bioturbation to modern levels. This would also lead to a 7–30 fold drop in α. Bioturbation was, however, still not as efficient as in modern oceans during the Cambrian Stage 2–3 event. Indeed, the maximum depth of bioturbation was high (up to 1 metre; Mangano and Buatois, 2014), but the degree of mixing was limited and the lateral extent of mixing were likely restricted to only the inner part of the continental shelves (Mangano and Buatois, 2014; Tarhan et al., 2015). Our model is designed to understand the effect of enhanced organic rain rate on the coupled C and S cycles, so we keep α constant and high during the event (3-30 fold higher than today, Table S-8 and Table S-18).
Eqs. S-18 and S-21 can be combined into one equation that relates organic carbon burial and pyrite sulphur burial via the proportionality constant, α, and remineralisation:
Eq. S-22
JPY = α * ƒREMIN / (1 - ƒREMIN) * JORG
This equation states that for a given set of the fluxes JORG and JPY (consistent with isotopic constraints), there will be a unique relationship between α and fREMIN.
In summary, there are five equations (S-16, S-17, S-19, S-20 and S-22) with a total of ten unknown parameters (δIN,C, ΔC, δIN,S, ΔS, JCARB, JEVAP, α, fREMIN, JORG, JPY) that describe the consequences for the global marine C and S cycles when organic carbon export to the seafloor is subject to change.
Model estimates for increases in organic carbon export during the Cambrian Stage 2–3 oxygenation episode
We use the carbon and sulphur isotope compositions of the ocean to calculate how increases in the export organic matter to sediments would drive changes in fREMIN, JORG and JPY during the event.
In our model simulations we enhance organic carbon export to the seafloor (increasing JRAIN) while keeping seven parameters constant in each model run (δIN,C, ΔC, δIN,S, ΔS, JCARB, JEVAP, α). The oceans are assumed in quasi-steady state with respect to C and S sinks and sources before the event and at the peak of the event (as explained above). As a first step, we utilise Eqs. S-17 and S-20 to get estimates for fORG and fPY prior to the event and at the peak of the event using the isotope compositions of the ocean derived from our data. Therefore, the f-ratios for the marine C and S cycle during the Cambrian Stage 2–3 event changed as shown in Table S-10. The propagated uncertainties are derived from the range of parameter values from Table S-8.
Table S-10 Ratios between reducing and oxidising sinks for carbon and sulphur changed during the Cambrian Stage 2–3 event.
| Before the event | At the peak | Behaviour | Modern value | |
| δ13C | 0 ‰ | 3 ‰ | increase | 0 ‰ |
| δ34S | 28 ‰ | 40 ‰ | increase | 21 ‰ |
| ƒORG /(1-ƒORG) | 0.21 ± 0.06 | 0.40 ± 0.10 | increase | 0.25 |
| ƒPY/(1-ƒPY) | 0.81 ± 0.51 | 6.21 ± 5.29 | increase | 0.56 |
Table S-10 shows that while there is an increase in the reducing sink for carbon (organic C burial) it was still subsidiary to the oxidising sink (carbonate burial), whereas there was a remarkable increase of the reducing sink for S (pyrite sulphur burial flux) which is ~6-fold greater than S burial in evaporites during the event.
For a given set of constraints on the three parameters—JCARB, JEVAP, and α—the three variables (fREMIN, JORG, JPY) can be adjusted to fit the observed isotope stratigraphy. First, we assume JCARB, JEVAP, and α were at their modern values (Table S-11). The model implies that the organic export (JRAIN) to the seafloor exceeded modern values by 2–15 times, and that the fraction of organic carbon remineralised (fREMIN) was even larger than today (>0.87). With slower organic sinking rates and less labile organic matter exported available for remineralisation in the sediments (Logan et al., 1995), such a scenario appears unrealistic.
Table S-11 Consequences for absolute organic carbon and pyrite sulphur flux, assuming modern-day values for JCARB, JEVAP, and α. The other constants are δIN, C = –5 ‰, δIN, S = 8 ‰, ΔS = 35 ‰, ΔBIO = 26 ‰. Flux unit: mol/yr.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 440·1012 | 3190·1012 | increase | 192 ·1012 |
| JORG | 52·1012 | 96·1012 | increase | 26 ·1012 |
| JPY | 2.8·1012 | 22·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.88 | 0.97 | increase | 0.87 |
However, previous models suggest a larger proportion of total sulphide produced by sulphate reduction (a 7–30 fold increase over the modern) formed pyrite in the sediments during the early Cambrian (Canfield and Farquhar, 2009). If we take this into consideration within our model, this leads to a proportional increase in the value of α and more realistic estimates for the remineralisation in global sediments. The consequence of a 10-fold increase in α is shown in Table S-12. In these estimates, we have kept all oxidative burial fluxes (JCARB, JEVAP) at modern values.
Table S-12 Calculations with α = 0.070 (= 10 x modern). The higher α value leads to a solution with more modest organic load fluxes and less remineralisation, fREMIN < 0.76.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 90·1012 | 406·1012 | increase | 192 ·1012 |
| JORG | 50·1012 | 93·1012 | increase | 26 ·1012 |
| JPY | 2.8·1012 | 22·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.43 | 0.76 | increase | 0.87 |
Results from this modelling exercise indicate plausible scenarios with high organic rain flux, high organic carbon and pyrite burial fluxes produce acceptable solutions. However the solution space also includes significantly smaller estimates for the organic export fluxes to the sediments. Due to limited vegetative cover coverage on land during the Cambrian, weathering fluxes were likely lower than today; the expansion of land plants is thought to increase Ca weathering ~4 fold in the Mid-Palaeozoic (Moulton and Berner, 1989; Lenton et al., 2012; Quirk et al., 2015). This would imply that carbonate and gypsum burial fluxes (JCARB, JEVAP) may also have been smaller than today, due to the reduced Ca fluxes to the oceans. The consequence on our calculations is shown in Table S-13.
Table S-13 Calculations with oxidative burial fluxes (JCARB, JEVAP) set at 1/4 of modern values. α set at 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 23·1012 | 100·1012 | increase | 192 ·1012 |
| JORG | 13·1012 | 24·1012 | increase | 26 ·1012 |
| JPY | 0.70·1012 | 5.6·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.43 | 0.76 | increase | 0.87 |
Generally, the estimated fREMIN values are not constant when JCARB and JEVAP are changed. This is the case in the example, Table S-13 vs Table S-12, simply because JCARB/JEVAP is constant (both JCARB and JEVAP change by a factor 1/5), implying JORG/JPY remains the same, and therefore the same fREMIN is derived in Eq. S-23.
Alternatively, lower peak pyrite S burial fluxes are calculated, if the average sulphur isotopic difference associated with pyrite burial was larger than 35 ‰. The consequences of ΔS = 50 ‰ are shown in Table S-14 (compare to Table S-11).
Table S-14 Calculations with ΔS set at 50 ‰ (as opposed to 35 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 69·1012 | 145·1012 | increase | 192 ·1012 |
| JORG | 50·1012 | 93·1012 | increase | 26 ·1012 |
| JPY | 1.4·1012 | 3.7·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.27 | 0.35 | increase | 0.87 |
Also lower pyrite S burial fluxes are calculated, if the isotope composition of the oceanic S input was greater than 8 ‰ (e.g., Halevy et al., 2012). For example, the consequences of δIN,S = 16 ‰ are shown in Table S-15 (compare to Table S-11).
Table S-15 Calculations with δIN,S set at 16 ‰ (as opposed to 8 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 67·1012 | 159 ·1012 | increase | 192 ·1012 |
| JORG | 50·1012 | 93 ·1012 | increase | 26 ·1012 |
| JPY | 1.1·1012 | 4.6 ·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.23 | 0.40 | increase | 0.87 |
JORG and JPY decline with higher δIN,C, but the change is small for changes in δIN,C (+1 ‰). The 1 % shift could occur with additional ~20 % increase in the carbonate weathering flux relative to average carbon input flux to the oceans (compare Table S-16 vs. Table S-11).
Table S-16 Calculations with δIN,C set at –4 ‰ (as opposed to –5 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 71·1012 | 373·1012 | increase | 192 ·1012 |
| JORG | 31·1012 | 61·1012 | increase | 26 ·1012 |
| JPY | 2.8·1012 | 22·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.55 | 0.83 | increase | 0.87 |
JORG and JPY estimates decline with higher ΔBIO, but the magnitude of change is small for any plausible variation of the average C isotopic difference expressed in marine sediments ΔBIO (+ 4‰, assumed). Compare Table S-17 vs. Table S-11.
Table S-17 Calculations with ΔBIO = 30 ‰ (as opposed to 26 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 82·1012 | 388·1012 | increase | 192 ·1012 |
| JORG | 42 ·1012 | 76 ·1012 | increase | 26 ·1012 |
| JPY | 2.8 ·1012 | 22 ·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.47 | 0.80 | increase | 0.87 |
In summary, several scenarios of enhanced organic export to the seafloor would simultaneously lead to the observed magnitudes of the δ13C and δ34S excursions. Importantly, the various model examples presented and discussed above show that organic carbon export to the seafloor could have increased by a factor of 2–6 during the event (Table S-18). Favoured models include higher values for α consistent with less sediment mixing by bioturbation suggestive of ~10-fold decrease in sulphide loss via oxidation. In addition, a higher S isotopic difference ΔS = 50 ‰, a higher δIN,S = 16 ‰, and/or smaller oxidative C and S burial fluxes than today are scenarios that also produce acceptable solutions.
Table S-18 Summary of selected solutions and the increasing organic rain rate during the Cambrian Stage 2–3 event.
| Case | Example | Initial JRAIN | Increase of JRAIN | ƒREMIN |
| Modern oceans | 219·1012 | 87 % | ||
| 1 | Higher α (10-fold, α = 0.072) (Table S-12) | 90·1012 | x 4.5 | 43 to >76 % |
| 1b | Higher α (3-fold, α = 0.022) | 181·1012 | x 6.3 | 71 to >91 % |
| 1c | Higher α (30-fold, α = 0.22) | 64·1012 | x 3.1 | 20 to >52 % |
| 2 | Case 1 + smaller JCARB, JEVAP (1/5) (Table S-13) | 23·1012 | x 4.5 | 43 to >76 % |
| 3 | Case 1 + higher ΔS (50 ‰) (Table S-14) | 71·1012 | x 2.1 | 27 to >35 % |
| 4 | Case 1 + higher δIN,S (16 ‰) (Table S-15) | 67·1012 | x 2.4 | 23 to >40 % |
S6. Model: Oxygenation dynamics during the Cambrian Stage 2–3 event
In our conceptual model for the oxygen dynamics during the event (Fig. 3), the appearance of large animals with guts expands the oxygenated zone in the upper ocean while bioturbating animals respond slowly to cause deoxygenation of the atmosphere and oceans as a whole. The feedbacks at play are illustrated in Figure S-10.
Onset of event
The emergence of larger animals with guts in the pelagic zone enhances the average sinking rate of organic particulates in the oceans. Once marine organic matter begins to sink faster through the water column, it enhances the organic load onto the seafloor and fuels more anaerobic remineralisation in (primarily unbioturbated) sediments. With less aerobic consumption in the oceans, oceans become more oxygenated. Accordingly, this evolutionary event would trigger ocean oxygenation at a characteristic time scale, τEVOL, dictated by the radiation of the relevant pelagic fauna (Fig. S-10, red arrow).
Our model assumes sinking rates of organic matter have forever increased, and that two stabilising feedback loops slowly acted to dampen oceanic oxygen levels via the effect on atmospheric pO2.
Stabilisation
With more food and O2 at the benthos over greater areas of the continental shelves, this reorganisation of the marine carbon (and sulphur) cycle would promote bioturbation (e.g., the proportion of organic carbon burial that occurs in bioturbated sediments, fbiot (Boyle et al., 2014). Bioturbation both enhances aerobic remineralisation in sediments (Fig. S-10, green arrow) and limits the availability of the ultimate limiting nutrient for new photosynthetic production: phosphate (Boyle et al., 2014) (Fig. S-10, blue arrow). Both effects lead to stabilising feedbacks that limit organic carbon burial, which is the principal source of atmospheric pO2 in all Earth system models (Bergman et al., 2004; Berner, 2006).
The slowest process involved in the feedback loops ultimately dictates the rate of the response to ocean oxygenation at this time. Here, a) τbiot is the characteristic time scale for bioturbating fauna to exploit the new habitats; b) τPO4 is the residence time of P in the Cambrian oceans; c) τPP and d) τSINK are the characteristic time scales for marine primary producers to respond to changing P availability (awaiting the response of the proximate limiting nutrients, e.g., N2-fixation) and the characteristic travel time for organic matter in the oceans, respectively. The characteristic time scales for remineralisation of organic matter in the sediments and in the water column are denoted τREMIN, SED, and τREMIN,WC, respectively. Lastly, the characteristic time scale associated with changing atmospheric O2 levels is given by the residence time of atmospheric O2 with respect to organic carbon burial:
Eq. S-23
τpO2 = MO2 / JORG
Although, the Cambrian rates are generally not known, we can assume that rates of organic production and remineralisation (τPP, τSINK, τREMIN, SED, and τREMIN,WC) and evolution (τbiot) are fast compared to the response time of the biogeochemical cycles (τPO4 and τpO2). Today, τPO4 ~15–50 kyr (Sarmiento and Gruber, 2006) and τpO2 ~ 1 Myrs (Bergman et al., 2004; Berner, 2006), which means the feedback loop responds on a time scale dictated by the size of the atmospheric O2 inventory and marine organic carbon burial flux (Eq. S-23).
Therefore, in our model the time scale of the Cambrian Stage 2–3 oxygenation episode (1.3 ± 0.8 Myrs Maloof et al., 2010a), see calculation in Methods, Samples and Geological Settings) constrain the atmospheric O2 inventory relative to the organic carbon burial flux, because the slow deoxygenation is dictated by the rate at which slower organic burial leads to decreasing atmospheric O2. If we assume that it took between 1/2 and 1 times the falling limb of the deoxygenation trend, that is between 325 ± 200 and 650 ± 400 kyr, we obtain a ballpark estimate for the Cambrian Stage 2 atmospheric pO2 to be 26 and 52 % PAL (present atmospheric level). However, the lack of a terrestrial biosphere at this time, accounting for ~33 % of modern day organic burial (Burdige, 2007), means that a corrected estimate for Cambrian Stage 2 atmospheric pO2 is 17–35 % PAL. This estimate is, however, proportional to the actual global organic carbon burial flux during the falling limb of the C and U excursion.
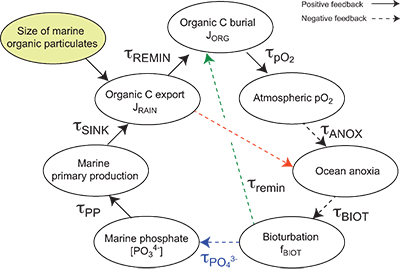
Figure S-10 Feedback diagram showing the oxygenation dynamics of the atmosphere-ocean system in response to increasing sinking rates of particulate organic matter in the oceans by larger animals with guts. See text for details.
Extended Data
Extended data 1
Table S-19 Elemental and isotope data for samples from the Sukharikha River Section. Reference materials include IAPSO seawater, argillaceous limestone (SRM-1d), carbonatite (COQ-1) and Columbia River basalt (BCR-2). rpt = repeated analyses.
| Sample | Strat. height (m) | Age* (Ma) | Th (ppb) | U (ppb) | U/Th | δ238U (‰) | ± 2SE (‰) | n | U EFTh ƒ | Mg/Ca | Al/Ca | Fe/Ca | Mn/Sr | Sr/Ca |
| Sukharikha River Section (A), Krasnoporog Fm | ||||||||||||||
| A393 | 624.6 | 519.81 | 301 | 93 | 0.31 | -0.667 | 0.032 | 5 | 0.2 | 0 | 0 | 0 | 0.45 | 0.0015 |
| A388 | 619.6 | 519.98 | 249 | 83 | 0.33 | -0.686 | 0.021 | 5 | 0.3 | 0 | 0 | 0 | 0.65 | 0.0013 |
| A384 | 615.6 | 520.12 | 408 | 39 | 0.09 | -0.6 | 0.02 | 1 | -0.7 | 0 | 0 | 0 | 0.82 | 0.0012 |
| A379 | 610.6 | 520.29 | 155 | 60 | 0.39 | -0.433 | 0.043 | 5 | 0.5 | 0.02 | 0 | 0.01 | 0.89 | 0.0014 |
| A376 | 607.6 | 520.39 | 221 | 169 | 0.77 | 1.9 | 0.0018 | |||||||
| - rpt | 607.6 | 520.39 | 228 | 214 | 0.94 | -0.63 | 0.015 | 5 | 2.6 | 0.89 | ||||
| A372 | 603.6 | 520.53 | 449 | 54 | 0.12 | -0.517 | 0.026 | 3 | -0.5 | 0.0014 | ||||
| - rpt | 603.6 | 520.53 | 333 | 44 | 0.13 | -0.5 | 0.01 | 0 | 0.02 | 0.76 | ||||
| A368 | 599.6 | 520.66 | 317 | 196 | 0.62 | -0.432 | 0.027 | 5 | 1.4 | 0.01 | 0 | 0.01 | 0.56 | 0.0016 |
| A366 | 597.6 | 520.73 | 275 | 445 | 1.62 | -0.542 | 0.023 | 5 | 5.2 | 0.02 | 0 | 0.01 | 0.52 | 0.0014 |
| A364 | 595.6 | 520.8 | 231 | 90 | 0.39 | -0.625 | 0.015 | 5 | 0.5 | 0.01 | 0 | 0.01 | 0.52 | 0.0013 |
| A361 | 592.6 | 520.9 | 352 | 82 | 0.23 | -0.569 | 0.015 | 3 | -0.1 | 0.01 | 0 | 0.01 | 0.46 | 0.0016 |
| A358 | 589.6 | 521 | 487 | 142 | 0.29 | -0.643 | 0.025 | 5 | 0.1 | 0.02 | 0 | 0.02 | 0.71 | 0.0014 |
| Malaya Kuonamka River Section (K3), Emyaksin Fm | ||||||||||||||
| K3-18P | 21.5 | 521.4 | 268 | 120 | 0.45 | 0.7 | 0.03 | 0 | 0.02 | 1.52 | 0.0009 | |||
| K3-22P | 26 | 521.13 | 246 | 239 | 0.97 | 2.7 | 0.06 | 0 | 0.04 | 1.01 | 0.0014 | |||
| K3-26P | 30 | 520.89 | 456 | 54 | 0.12 | -0.5 | 0.03 | 0 | 0.02 | 2.12 | 0.0008 | |||
| K3-28P | 32 | 520.77 | 183 | 31 | 0.17 | -0.4 | 0.02 | 0 | 0.02 | 1.25 | 0.0011 | |||
| K3-30P | 34 | 520.65 | 310 | 54 | 0.17 | -0.3 | 0.05 | 0 | 0.03 | 1.38 | 0.0010 | |||
| K3-32P | 36 | 520.53 | 276 | 74 | 0.27 | 0.0 | 0.07 | 0 | 0.23 | 1.29 | 0.0014 | |||
| K3-35P | 39 | 520.35 | 418 | 49 | 0.12 | -0.6 | 0.02 | 0 | 0.02 | 0.74 | 0.0012 | |||
| K3-37P | 41 | 520.23 | 943 | 87 | 0.09 | -0.6 | 0.02 | 0 | 0.01 | 1.18 | 0.0009 | |||
| K3-39P | 43 | 520.11 | 338 | 34 | 0.10 | -0.6 | 0.02 | 0 | 0.02 | 1.29 | 0.0009 | |||
| K3-41P | 45 | 519.99 | 348 | 39 | 0.11 | -0.6 | 0.03 | 0 | 0.02 | 1.65 | 0.0010 | |||
| Bol'shaya Kuonamka (K6), Emyaksin Fm | ||||||||||||||
| K6-24 | 23 | 521.4 | 569 | 151 | 0.26 | 0.0 | 0.05 | 0 | 0.02 | 1.03 | 0.0012 | |||
| K6-27 | 26 | 521.15 | 363 | 67 | 0.19 | -0.3 | 0.04 | 0 | 0.02 | 1.44 | 0.0012 | |||
| K6-30 | 29 | 520.89 | 568 | 65 | 0.12 | -0.6 | 0.06 | 0.01 | 0.02 | 1.62 | 0.0011 | |||
| K6-31A | 30 | 520.81 | 615 | 137 | 0.22 | -0.1 | 0.02 | 0 | 0.02 | 0.98 | 0.0015 | |||
| K6-34 | 33 | 520.55 | 815 | 111 | 0.14 | -0.5 | 0.07 | 0 | 0.01 | 1.44 | 0.0013 | |||
| K6-35 | 34 | 520.47 | 475 | 72 | 0.15 | -0.4 | 0.02 | 0.01 | 0.01 | 0.97 | 0.0047 | |||
| K6-38 | 37 | 520.21 | 380 | 66 | 0.17 | -0.3 | 0.01 | 0 | 0.01 | 0.76 | 0.0009 | |||
| K6-39 | 38 | 520.13 | 312 | 46 | 0.15 | -0.4 | 0.01 | 0 | 0.02 | 1.35 | 0.0008 | |||
| K6-40 | 39 | 520.04 | 251 | 178 | 0.71 | 1.7 | 0.01 | 0 | 0 | 1.00 | 0.0009 | |||
| Reference materials | ||||||||||||||
| IAPSO seawater¬ | -0.342 | 0.022 | 5 | |||||||||||
| SRM-1d | 77 | 743 | 9.64 | -0.083 | 0.017 | 7 | 36.8 | 0.01 | 0.01 | 0.09 | ||||
| - rpt | 70 | 478 | 6.87 | -0.089 | 0.024 | 2 | 26.2 | 0 | 0 | 0 | ||||
| SRM-1d † | 5475 | 1475 | 0.27 | -0.105 | 0.017 | 7 | 1 | 0 | 0 | 0.01 | ||||
| COQ-1 † | 112 | 727 | 6.51 | -0.337 | 0.024 | 5 | 24.9 | 0.08 | 0.03 | 0.2 | ||||
| BCR-2 † | -0.274 | 0.017 | 5 | |||||||||||
| BCR-2 † | -0.255 | 0.013 | 4 | |||||||||||
| BCR-2 † | -0.24 | 0.009 | 5 | |||||||||||
*Age model based on δ13C chemostratigraphy after Maloof et al. (2010a).
Samples marked with † are whole-rock analysis, all others are mild acetic leaches (see methods for details).
¬) The processing of IAPSO seawater followed the procedure of Weyer et al. (2008).
ƒ) Uranium Enrichment factor is calculated as follows: U EFTh = (U/Th) /(U/Th)UCC, where the UCC stands for upper continental crust with a U/Th = 0.26
Extended data 2
Table S-20 Mineralogical data for samples from the Sukharikha River section.
| Sample | Calcite | Quartz | Dolomite | Ankerite | Chlorite (Clinochlore) | Mica | K-Feldspar | Haematite | sum |
| wt. % | wt. % | wt. % | wt. % | wt. % | wt. % | wt. % | wt. % | ||
| Sukharikha River Section. Igarka River. NW Siberia | |||||||||
| A393 | 93 | 2 | 0 | 1 | 1 | 3 | 100 | ||
| A388 | |||||||||
| A384 | 88 | 4 | 0 | 1.5 | 1.75 | 4.5 | 0.25 | 92 | |
| A379 | 56 | 25.5 | 8 | 0 | 2 | 8.5 | 66 | ||
| A376 | 85 | 11 | <5 | 0.5 | 1 | 0.5 | 2.5 | 97.5 | |
| A372 | |||||||||
| A368 | 76 | 7 | 4 | 2.5 | 4 | 2 | 4.5 | 95.5 | |
| A366 | 79 | 5 | 6.5 | 1.5 | 1 | 1 | 6 | 100 | |
| A364 | 90 | 5 | 0 | 1 | 0.5 | 3.5 | 96 | ||
| A361 | 90 | 2 | 0.5 | 0.5 | 0.5 | 1 | 5.5 | 94 | |
| A358 | 71 | 4 | 9.5 | 9.5 | 6 | 3 | 7.5 | 103 | |
| Bolshaya Kuonamka. Anabar Uplift. Section 96-6 | |||||||||
| K6-24 | 88 | 4 | 1.5 | 2 | 2.5 | 2 | 97.5 | ||
| K6-27 | 85 | 4 | 4 | 2.5 | 2 | 2 | 0.5 | 97 | |
| K6-30 | 80 | 4 | 8 | 3 | 2 | 2.5 | 0.5 | 97 | |
| K6-31A | 90 | 4 | 0.5 | 1 | 2 | 1.5 | 1.5 | < 0.5 | 97.5 |
| K6-31B | 86 | 4.5 | 0.5 | 1.5 | 2 | 2.5 | 2.5 | 0.5 | 90 |
| K6-34 | 76 | 5 | 3 | 6.5 | 3 | 2.5 | 3 | 1 | 97.5 |
| K6-35 | 82 | 5.5 | 3.5 | 2 | 2.5 | 2 | 2.5 | 89.5 | |
| K6-38 | 91 | 3 | 0.5 | 0.5 | 1 | 2 | 2 | 100 | |
| K6-39 | 87 | 4.5 | 1 | 1.5 | 2 | 2 | 2 | < 0.5 | 95.5 |
| K6-40 | 84 | 2 | 0.5 | 1.5 | 1.5 | 0.5 | 86.5 | ||
Muscovite and Apatite-OH were looked for, but not detected, in the samples.
Download in ExcelTable S-21 Sulphur isotope data of carbonate associated sulphate and total organic carbon content in samples from three Siberian sections (Sukharika River (A), Bolshaya Kuonamka river (K3), and Malaya Kuonamka river (K6)). Published C and O isotope data are shown for comparison (Kouchinsky et al., 2007).
| Sample | Age assigned | TOC | δ34S | δ13C | δ18O |
| Ma | wt. % | ‰ (V-CDT) | ‰ (V-PDB) | ‰ (V-PDB) | |
| Sukharikha River Section, Krasnoporog Fm | |||||
| A350 | 521.27 | 0.04 | 30.48 | -1.48 | -6.85 |
| A358 | 521 | 0.04 | 32.58 | -1.27 | -6.9 |
| A364 | 520.8 | 0.04 | 39.53 | 0.09 | -7.24 |
| A366 | 520.73 | 0.03 | 38.27 | 0.67 | -6.6 |
| A368 | 520.66 | 0.03 | 37.41 | 1.29 | -6.58 |
| A372 | 520.53 | 0.03 | 39.37 | 1.56 | -7.12 |
| A376 | 520.39 | 0.02 | 2.63 | -6.79 | |
| A379 | 520.29 | 0.02 | 37.5 | 2.03 | -6.59 |
| A384 | 520.12 | 0.03 | 1.09 | -6.98 | |
| A388 | 519.98 | 0.03 | 35.02 | 0.07 | -6.94 |
| A393 | 519.81 | 0.02 | -0.5 | -7.15 | |
| Malaya Kuonamka River Section (K3), Emyaksin Fm | |||||
| K3-18P | 521.4 | 0.033 | 27.93 | -1.29 | -6.24 |
| K3-22P | 521.13 | 0.159 | -1.1 | -5.78 | |
| K3-26P | 520.89 | 0.025 | 27.93 | -0.72 | -5.99 |
| K3-28P | 520.77 | 0.032 | 33.27 | 0.22 | -5.96 |
| K3-30P | 520.65 | 0.028 | 36.16 | 0.97 | -5.57 |
| K3-32P | 520.53 | 0.024 | 35.2 | 1.76 | -5.62 |
| K3-35P | 520.35 | 0.026 | 39.03 | 2.43 | -5.8 |
| K3-37P | 520.23 | 0.018 | 1.72 | -5.92 | |
| K3-39 | 520.11 | 0.027 | 1.03 | -5.88 | |
| K3-41 | 519.99 | 0.131 | 0.23 | -6.32 | |
| Bol'shaya Kuonamka (K6), Emyaksin Fm | |||||
| K6-24 | 521.4 | 0.046 | -1.22 | -6.01 | |
| K6-27 | 521.15 | 0.05 | 28.03 | -1.02 | -6.26 |
| K6-30 | 520.89 | 0.097 | 28.81 | -0.54 | -6.07 |
| K6-31 | 520.81 | 0.035 | 32.35 | 0.21 | -6.18 |
| K6-32 | 520.72 | 0.062 | 0.99 | -5.91 | |
| K6-34 | 520.55 | 0.041 | 36.86 | 1.8 | -5.42 |
| K6-35 | 520.47 | 0.1 | 2.63 | -5.49 | |
| K6-38 | 520.21 | 0.024 | 1.81 | -5.65 | |
| K6-39 | 520.13 | 0.095 | 34.93 | 1.27 | -5.84 |
| K6-40 | 520.04 | 0.11 | -5.95 | ||
Table S-22 Data sources for the marine redox proxy data (Mo, U, δ98Mo and δ238U) from Late Ediacaran and Cambrian sedimentary archives (modified after Boyle et al., 2014). All Mo isotope data were corrected from in-house reference materials to the NIST SRM 3136 scale (Goldberg et al., 2013; Nägler et al., 2014).
| Formation | Locality | Biozone | Lithology | Age (max) | Age (min) | Mo | U | Mo/TOC | U/TOC | δ98Mo | δ98Mo ref ‰ offset from NIST 3136 at 0.25‰ | References |
| Dictyonema Shales | Sweden | Shale | 482 | √ | Quinby-Hunt et al.(1989) | |||||||
| Alum Shale | Albjära, Sweden | Cambrian Series 4 | Shale | 485 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Alum Shale | Gislövhammar, Sweden | Cambrian Series 4 | Shale | 485 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Alum Shale | Cambrian Series 4 | Shale | 499 | √ | √ | Lewan and Buchardt (1989) | ||||||
| Alum Shale | Cambrian Series 4 | Shale | 499 | √ | √ | Partin et al. (2013) | ||||||
| Alum Shale | Andrarum-3, Sweden | Cambrian Series 3-4 | Shale | 500 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Alum Shale | Andrarum-3, Sweden | Cambrian Series 3-4 | Shale | 500 | √ | √ | √ | 0.08 | Gill et al. (2011) (except δ98Mo) | |||
| Alum Shale | Närke Area, Sweden | Shale | 505 | 499 | √ | √ | √ | Leventhal (1991) | ||||
| Burgess Shale | Canada | Cambrian Series 3 | Shale | 505 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Hay River | Georgina Basin, Australia | Shale | 505 | √ | √ | Donnelly et al. (1988) | ||||||
| Niutitang | Zunyi, South China | Cambrian Stage 3 | Shale | 520 | √ | √ | Jiang et al. (2006) | |||||
| Niutitang | Zhangjiajie | Cambrian Stage 3 | Shale | 520 | 520 | √ | √ | Jiang et al. (2006) | ||||
| Niutitang | Dingtai | Cambrian Stage 3 | Shale | 521 | 517 | √ | √ | √ | Xu et al. (2012) | |||
| Niutitang | Maluhe | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | Xu et al. (2012) | ||||
| Niutitang | Dazhuliushui | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | Xu et al. (2012) | ||||
| Niutitang | Sancha | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | Xu et al. (2012) | ||||
| Niutitang | Ganziping | Cambrian Stage 3 | Shale | 521 | 520 | √ | √ | √ | √ | Lehmann et al. (2007) | ||
| Niutitang | Yuanling | Cambrian Stage 3 | Shale | 521 | 520 | √ | √ | √ | √ | Lehmann et al. (2007) | ||
| Yuertushi | Xiaoerbulaki, Tarim Basin, NW China | Cambrian Stage 2 | Shale | 521 | √ | √ | √ | Yu et al. (2009) | ||||
| Yuertushi | Sugaitebulaki, Tarim Basin, NW China | Cambrian Stage 2 | Shale | 521 | √ | √ | Yu et al. (2009) | |||||
| Niutitang | Maluhe | Cambrian Stage 3 | Shale | 521 | √ | Lehmann et al. (2007) | ||||||
| Yu’anshan | Chengjiang, South China | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Niutitang | Ganziping | Cambrian Stage 3 | Shale | 521 | 520 | √ | Wille et al. (2008) | |||||
| Niutitang | Yuanling | Cambrian Stage 3 | Shale | 521 | 520 | √ | Wille et al. (2008) | |||||
| Yuanshan | Xiaotan, China | Cambrian Stage 3 | Shale | 521 | 518 | √ | √ | Och et al. (2013) | ||||
| Yuanshan | Dapotuo, China | Cambrian Stage 3 | Shale | 521 | 518 | √ | √ | Och et al. (2013) | ||||
| Niutitang | Zhongnan, China | Cambrian Stage 3 | Shale | 521 | 520 | √ | √ | Och et al. (2013) | ||||
| Niutitang | Dazhuliushui | Cambrian Stage 3 | Shale | 521 | √ | √ | Och et al. (2013) | |||||
| Niutitang | Maluhe | Cambrian Stage 3 | Shale | 521 | √ | √ | Och et al. (2013) | |||||
| Niutitang | Cili | Cambrian Stage 3 | Shale | 521 | √ | √ | Och et al. (2013) | |||||
| Guojiaba | Songtao section, South China | Cambrian Stage 2-3 | Shale | 524 | 508 | √ | √ | √ | √ | Guo et al. (2007) | ||
| Jiumenchong | Songtao section, South China | Cambrian Stage 2-3 | Shale | 524 | 520 | √ | √ | √ | √ | Guo et al. (2007) | ||
| Shiyantou | Meischucun, China | Cambrian Stage 2 | Shale | 524 | 522 | √ | √ | Och et al. (2013) | ||||
| Shiyantou | Dapotuo, China | Cambrian Stage 2 | Shale | 524 | 522 | √ | √ | Och et al. (2013) | ||||
| Shiyantou | Xiaotan, China | Cambrian Stage 2 | Shale | 529 | 521 | √ | √ | Och et al. (2013) | ||||
| Shiyantou | Meischucun, SYT | Cambrian Stage 2 | Shale | 529 | 521 | √ | √ | √ | Wen et al. (2011) | |||
| Hetang | Cambrian Stage 3 | Shale | 531 | √ | Zhou and Jiang (2009) | |||||||
| Ara Group | ALNR-1, Oman | Ediacaran-Cambrian | Shale | 540 | √ | √ | Wille et al. (2008) | |||||
| Ara Group | MM NW-1, Oman | Ediacaran-Cambrian | Shale | 540 | √ | √ | Wille et al. (2008) | |||||
| Ara Group | MM NW-1, Oman | Ediacaran-Cambrian | Shale | 542 | √ | Schröder and Grotzinger (2007) | ||||||
| Dengying | Ediacaran Series 2 | Shale | 545 | √ | Partin et al. (2013) | |||||||
| Dengying | Ediacaran Series 2 | Shale | 545 | √ | √ | Guo et al. (2007) | ||||||
| Liuchapo | Ediacaran Series 2 | Shale | 545 | √ | √ | Guo et al. (2007) | ||||||
| Dengying | Songtao section, South China | Shale | 545 | √ | Guo et al. (2007) | |||||||
| Nama Group | Namibia | Ediacaran Series 2 | Shale | 548 | √ | McLennan et al. (1983) | ||||||
| Doushantuo | Songtao section,South China | Shale | 551 | √ | Partin et al. (2013) | |||||||
| Doushantuo | Songtao section,South China | Shale | 551 | √ | Guo et al. (2007) | |||||||
| Isaac | Castle Creek + Cariboo Mountains, Windermere, Canada | Shale | 565 | √ | 0.08 | Dahl et al. (2010) | ||||||
| Drook | New Foundland, Canada | Shale | 565 | √ | √ | √ | 0.08 | Dahl et al. (2010) | ||||
| Doushantuo, Cycle 3 | Jiulongwan, Zhongling, Minle, Longe Nanhua Basin, South China | Shale | 565 | 555 | √ | √ | Li et al. (2010) | |||||
| Gaskiers | New Foundland, Canada | Shale | 580 | √ | √ | √ | 0.08 | Dahl et al. (2010) | ||||
| Upper Kaza | Windermere, Canada | Shale | 580 | √ | √ | √ | 0.08 | Dahl et al. (2010) |
Supplementary Information References
Andersen, M.B., Elliott, T., Freymuth, H., Sims, K.W., Niu, Y., Kelley, K.A. (2015) The terrestrial uranium isotope cycle. Nature 517, 356–359.
Andersen, M.B., Vance, D., Morford, J.L., Bura-Nakić, E., Breitenbach, S.F.M., Och, L. (2016) Closing in on the marine 238U/235U budget. Chemical Geology 420, 11–22.
Archer, C., Vance, D. (2008) The isotopic signature of the global riverine molybdenum flux and anoxia in the ancient oceans. Nature Geoscience 1, 597–600.
Bergman, N.M., Lenton, T.M., Watson, A.J. (2004) COPSE: A new model of biogeochemical cycling over Phanerozoic time. American Journal of Science 304, 397–437.
Berner, R.A. (2006) GEOCARBSULF: A combined model for Phanerozoic atmospheric O2 and CO2. Geochimica et Cosmochimica Acta 70, 5653–5664.
Berner, E.K., Berner, R.A. (2012) Global environment: water, air, and geochemical cycles. Princeton University Press.
Boyle, R.A., Dahl, T.W., Dale, A.W., Shields-Zhou, G.A., Zhu, M., Brasier, M.D., Canfield, D.E., Lenton, T.M. (2014) Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nature Geoscience 7, 671–676.
Brasier, M.D., Rozanov, A.Y., Zhuravlev, A.Y., Corfield, R.M., Derry, L.A. (1994) A carbon isotope reference scale for the Lower Cambrian succession in Siberia: report of IGCP Project 303. Geological Magazine 131, 767–783.
Burdige, D.J. (2007) Preservation of Organic Matter in Marine Sediments: Controls, Mechanisms, and an Imbalance in Sediment Organic Carbon Budgets? Chemical Reviews 107, 467–485.
Canfield, D.E., Farquhar, J. (2009) Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proceedings of the National Academy of Sciences of the United States of America 106, 8123–8127.
Chen, X., Romaniello, S.J., Herrmann, A.D., Wasylenki, L.E., Anbar, A.D. (2016) Uranium isotope fractionation during coprecipitation with aragonite and calcite. Geochimica et Cosmochimica Acta 188, 189–207.
Condon, D.J., McLean, N., Noble, S.R., Bowring, S.A. (2010) Isotopic composition (238U/235U) of some commonly used uranium reference materials. Geochimica et Cosmochimica Acta 74, 7127–7143.
Connelly, J.N., Bizzarro, M., Krot, A.N., Nordlund, A., Wielandt, D., Ivanova, M.A. (2012) The absolute chronology and thermal processing of solids in the solar protoplanetary disk. Science 338, 651–655.
Dahl, T.W., Hammarland, E.U., Anbar, A.D., Bond, D.P.G., Gill, B.C., Gordon, G.W., Knoll, A.H., Nielsen, A.T., Schovsbo, N.H., Canfield, D.E. (2010) Devonian rise in atmospheric oxygen correlated to the radiations of terrestrial plants and large predatory fish. Proceedings of the National Academy of Sciences 107, 17911–17915.
Dahl, T.W., Canfield, D.E., Rosing, M.T., Frei, R.E., Gordon, G.W., Knoll, A.H., Anbar, A.D. (2011) Molybdenum evidence for expansive sulfidic water masses in ~750Ma oceans. Earth and Planetary Science Letters 311, 264–274.
Donnelly, T.H., Shergold, J.H., Southgate, P.N. (1988) Anomalous geochemical signals from phosphatic Middle Cambrian rocks in the southern Georgina Basin, Australia. Sedimentology 35, 549–570.
Dunk, R.M., Mills, R.A., Jenkins, W.J. (2002) A reevaluation of the oceanic uranium budget for the Holocene. Chemical Geology 190, 45–67.
Gill, B.C., Lyons, T.W., Young, S.A., Kump, L.R., Knoll, A.H., Saltzman, M.R. (2011) Geochemical evidence for widespread euxinia in the later Cambrian ocean. Nature 469, 80–83.
Goldberg, T., Gordon, G., Izon, G., Archer, C., Pearce, C.R., McManus, J., Anbar, A.D., Rehkämper, M. (2013) Resolution of inter-laboratory discrepancies in Mo isotope data: An intercalibration. Journal of Analytical Atomic Spectrometry 28, 724–735.
Guo, Q., Shields, G.A., Liu, C., Strauss, H., Zhu, M., Pi, D., Goldberg, T., Yang, X. (2007) Trace element chemostratigraphy of two Ediacaran–Cambrian successions in South China: Implications for organosedimentary metal enrichment and silicification in the Early Cambrian. Palaeogeography, Palaeoclimatology, Palaeoecology 254, 194–216.
Halevy, I., Peters, S.E., Fischer, W.W. (2012) Sulfate Burial Constraints on the Phanerozoic Sulfur Cycle. Science 337, 331–334.
Jeppsson, L., Anehus, R., Fredholm, D. (1999) The optimal acetate buffered acetic acid technique for extracting phosphatic fossils. Journal of Paleontology 73, 964–972.
Jiang, S-Y., Chen, Y.-Q,, Ling, H.-F., Feng, H.-Z., Ni, P. (2006) Trace- and rare-earth element geochemistry and Pb–Pb dating of black shales and intercalated Ni–Mo–PGE–Au sulfide ores in Lower Cambrian strata, Yangtze Platform, South China. Mineralium Deposita 41, 453–467.
Kaufman, A.J., Knoll, A.H. (1995) Neoproterozoic variations in the C-isotopic composition of seawater: stratigraphic and biogeochemical implications. Precambrian Research 73, 27–49.
Kaufman, A.J., Knoll, A.H., Semikhatov, M.A., Grotzinger, J.P., Jacobsen, S.B., Adams, W. (1996) Integrated chronostratigraphy of Proterozoic-Cambrian boundary beds in the western Anabar region, northern Siberia. Geological Magazine 133, 509–533.
Kendall, B., Creaser, R.A., Gordon, G.W., Anbar, A.D. (2009) Re–Os and Mo isotope systematics of black shales from the Middle Proterozoic Velkerri and Wollogorang Formations, McArthur Basin, northern Australia. Geochimica et Cosmochimica Acta 73, 2534–2558.
Kouchinsky, A., Bengtson, S., Missarzhevsky, V.V., Pelechaty, S., Torssander, P., Val'Kov, A.K. (2001) Carbon isotope stratigraphy and the problem of a pre-Tommotian Stage in Siberia. Geological Magazine 138, 387–396.
Kouchinsky, A., Bengtson, S., Pavlov, V., Runnegar, B., Torssander, P., Young, E., Ziegler, K. (2007) Carbon isotope stratigraphy of the Precambrian–Cambrian Sukharikha River section, northwestern Siberian platform. Geological Magazine 144, 1–10.
Kouchinsky, A., Bengtson, S., Runnegar, B., Skovsted, C., Steiner, M., Vendrasco, M. (2012) Chronology of early Cambrian biomineralization. Geological Magazine 149, 221–251.
Kouchinsky, A., Bengtson, S., Clausen, S., Vendrasco, M. (2015) A lower Cambrian fauna of skeletal fossils from the Emyaksin Formation, northern Siberia. Acta Palaeontologica Polonica 60, 421–512.
Kurtz, A.C. (2003) Early Cenozoic decoupling of the global carbon and sulfur cycles. Paleoceanography 18, 1090, doi: 10.1029/2003PA000908.
Lehmann, B., Naegler, T.F., Holland, H.D., Wille, M., Mao, J., Pan, J., Ma, D., Dulski, P. (2007) Highly metalliferous carbonaceous shale and Early Cambrian seawater. Geology 35, 403–406.
Lenton, T.M., Crouch, M., Johnson, M., Pires, N., Dolan, L. (2012) First plants cooled the Ordovician. Nature Geoscience 5, 86–89.
Leventhal, J.S. (1991) Comparison of organic geochemistry and metal enrichment in two black shales: Cambrian Alum Shale of Sweden and Devonian Chattanooga Shale of United States. Mineralium Deposita 26, 104–112.
Lewan, M.D., Buchardt, B. (1989) Irradiation of organic matter by uranium decay in the Alum Shale, Sweden. Geochimica et Cosmochimica Acta 53, 1307–1322.
Li, C., Love, G.D., Lyons, T.W., Fike, D.A., Sessions, A.L., Chu, X. (2010) A Stratified Redox Model for the Ediacaran Ocean. Science 328, 80–83.
Logan, G.A., Hayes, J.M., Hieshima, G.B., Summons, R.E. (1995) Terminal Proterozoic reorganization of biogeochemical cycles. Nature 376, 53–56.
Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010a) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
Maloof, A.C., Ramezani, J., Bowring, S.A., Fike, D.A., Porter, S.M., Mazouad, M. (2010b) Constraints on early Cambrian carbon cycling from the duration of the Nemakit-Daldynian-Tommotian boundary d13C shift, Morocco. Geology 38, 623–626.
Mangano, M.G., Buatois, L.A. (2014) Decoupling of body-plan diversification and ecological structuring during the Ediacaran-Cambrian transition: evolutionary and geobiological feedbacks. Proceedings of the Royal Society B. Biological Sciences 281, 20140038.
McClennan, S.M., Taylor, S.R., Kröner, A. (1983) Geochemical evolution of Archean shales from South Africa. I. The Swaziland and Pongola Supergroups. Precambrian Research 22, 93–124.
Miller, C.A., Peucker-Ehrenbrink, B., Walker, B.D., Marcantonio, F. (2011) Re-assessing the surface cycling of molybdenum and rhenium. Geochimica et Cosmochimica Acta 75, 7146–7179.
Morford, J.L., Emerson, S. (1999) The geochemistry of redox sensitive trace metals in sediments. Geochimica Et Cosmochimica Acta 63, 1735–1750.
Moulton, K.L., Berner, R.A. (1989) Quantification of the effect of plants on weathering: Studies in Iceland. Geology 26, 895–898.
Nägler, T.F., Anbar, A.D., Archer, C., Goldberg, T., Gordon, G.W., Greber, N.D., Siebert, C., Sohrin, Y., Vance, D. (2014) Geostandards and Geoanalytical Research 38, 149–151.
Noordmann, J., Weyer, S., Georg, R.B., Jons, S., Sharma, M. (2016) 238U/235U isotope ratios of crustal material, rivers and products of hydrothermal alteration: new insights on the oceanic U isotope mass balance. Isotopes in Environmental Health Studies 52, 141–163.
Och, L.M., Shields-Zhou, G.A., Poulton, S.W., Manning, C., Thirlwall, M.F., Li, D., Chen, X., Ling, H., Osborn, T., Cremonese, L. (2013) Redox changes in Early Cambrian black shales at Xiaotan section, Yunnan Province, South China. Precambrian Research 225, 166–189.
Partin, C.A., Bekker, A., Planavsky, N.J., Scott, C.T., Gill, B.C., Li, C., Podkovyrov, V., Maslov, A., Konhauser, K.O., Lalonde, S.V.,Love, G.D., Poulton, S.W., Lyons, T.W. (2013) Large-scale fluctuations in Precambrian atmospheric and oceanic oxygen levels from the record of U in shales. Earth and Planetary Science Letters 369–370, 284–293.
Quinby-Hunt, M.S., Wilde, P., Berry, W.B.N. (1989) Elementary geochemistry of black shales – statistical comparison of low-calcific shales with other shales. U.S. Geological Survey Circular 1037, 8–15.
Quirk, J., Leake, J.R., Johnson, D.A., Taylor, L.L., Saccone, L., Beerling, D.J. (2015) Constraining the role of early land plants in Palaeozoic weathering and global cooling. Proceedings of the Royal Society B. Biological Sciences 282, 20151115.
Romaniello, S. (2012) Incorporation and Preservation of Molybdenum and Uranium Isotope Variations in Modern Marine Sediments. PhD thesis, Arizona State University.
Rowland, S.M., Luchinina, V., Korovnikov, I.V., Sipin, D.P., Tarletskov, A.I., Fedoseev, A.V. (1998) Biostratigraphy of the Vendian–Cambrian Sukharikha River section, northwestern Siberian Platform. Canadian Journal of Earth Sciences 35, 339–352.
Rozanov, A., Khomentovsky, V., Shabanov, Y., Karlova, G., Valrlamov, A., Luchinina, V., Pegel, T., Demidenko, Y., Parkhaev, P., Korovnikov, I., Skorlotova, N. (2008) To the Problem of Stage Subdivision of the Lower Cambrian. Stratigraphy and Geological Correlation 16, 1–19.
Saltzman, M.R., Thomas, E. (2012) Carbon Isotope Stratigraphy. In: Gradstein, F.M., Ogg, J.G., Schmitz, M., Ogg, G. (Eds.) The Geological Time Scale. Elsevier, Boston, 207–232.
Sarmiento, J.L., Gruber, N. (2006) Ocean Biogeochemical Dynamics. Princeton university press, New Jersey, USA.
Schröder, S., Grotzinger, J.P. (2007) Evidence for anoxia at the Ediacaran–Cambrian boundary: the record of redox-sensitive trace elements and rare earth elements in Oman. Journal of the Geological Society of London 164, 175–187.
Scott, C., Lyons, T.W., Bekker, A., Shen, Y., Poulton, S.W., Chu, X., Anbar, A.D. (2008) Tracing the stepwise oxygenation of the Proterozoic ocean. Nature 452, 456–459.
Tarhan, L.G., Droser, M.L. (2014) Widespread delayed mixing in early to middle Cambrian marine shelfal settings. Palaeogeography, Palaeoclimatology, Palaeoecology 399, 310–322.
Tarhan, L.G., Droser, M.L., Planavsky, N.J., Johnston, D.T. (2015) Protracted development of bioturbation through the early Palaeozoic Era. Nature Geoscience 8, 865–869.
Tissot, F.L.H., Dauphas, N. (2015) Uranium isotopic compositions of the crust and ocean: Age corrections, U budget and global extent of modern anoxia. Geochimica et Cosmochimica Acta 167, 113–143.
Varlamov, A., Rozanov, A.Y., Khomentovsky, V., Shabanov, Y.Y., Abaimova, G., E, D.Y., Karlova, G., Korovnikov, I., Luchinina, V., Malakhovskaya, Y.E., Parkhaev, P.Y., Pegel, T., Skorlotova, N., Sundukov, V., Sukhov, S., Fedorov, A., Kipriyanova, L. (2008) The Cambrian System of the Siberian Platform. Part 1: The Aldan-Lena region. PIN-RAS, Moscow and Novosibirsk.
Wen, H., Carignan, J., Zhang, Y., Fan, H., Cloquet, C., Liu, S. (2011) Molybdenum isotopic records across the Precambrian–Cambrain boubdary. Geology 39, 775–778.
Weyer, S., Anbar, A.D., Gerdes, A., Gordon, G.W., Algeo, T.J., Boyle, E.A. (2008) Natural fractionation of 238U/235U. Geochimica et Cosmochimica Acta 72, 345–359.
Wille, M., Nägler, T.F., Lehmann, B., Schroder, S., Kramers, J.D. (2008) Hydrogen sulphide release to surface waters at the Precambrian/Cambrian boundary. Nature 453, 767–769.
Wotte, T., Shields-Zhou, G.A., Strauss, H. (2012) Carbonate-associated sulfate: Experimental comparisons of common extraction methods and recommendations toward a standard analytical protocol. Chemical Geology 326–327, 132–144.
Xu, L., Lehmann, B., Mao, J., Nägler, T.F., Neubert, N., Bottcher, M.E., Escher, P. (2012) Mo isotope and trace element patterns of Lower Cambrian black shales in South China: Multi-proxy constraints on the paleoenvironment. Chemical Geology 318–319, 45–59.
Yu, C., Peng, B., Tang, X., Xie, S., Yang, G., Yin, C., Tu, X., Liu, Q., Yang, K. (2009) Geochemical characteristics of soils derived from the lower-Cambrian black shales distributed in central hunan, China. Acta Pedologica Sinica 46, 557–570.
Zhou, C., Jiang, S.-Y. (2009) Palaeoceanographic redox environments for the lower Cambrian Hetang Formation in South China: Evidence from pyrite framboids, redox sensitive biota trace elements, and sponge occurrence. Palaeogeography, Palaeoclimatology, Palaeoecology 271, 279–286.
Figures and Tables
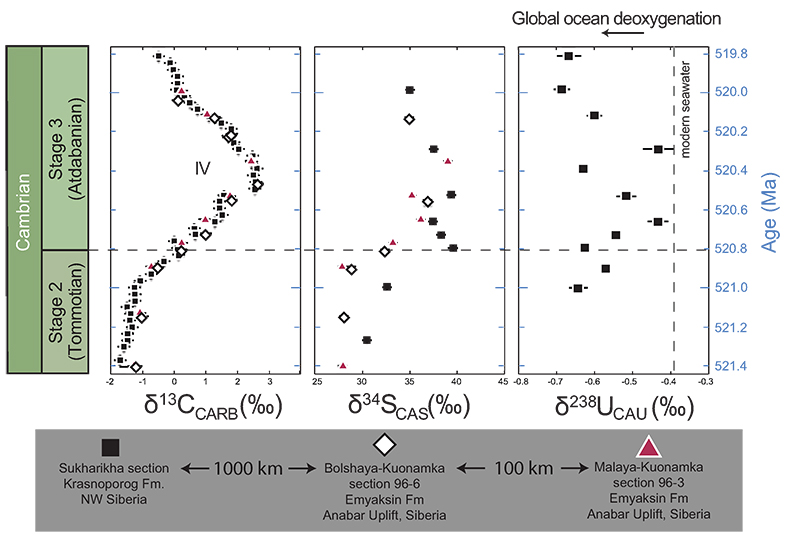
Figure 1 Isotope data from three carbonate successions straddling the Cambrian Stage 2–3 boundary (Cambrian Stage 2–3) in Siberia. Carbon isotope data from carbonate (δ13CCARB) is taken from Kouchinsky et al. (2007)
Kouchinsky, A., Bengtson, S., Pavlov, V., Runnegar, B., Torssander, P., Young, E., Ziegler, K. (2007) Carbon isotope stratigraphy of the Precambrian–Cambrian Sukharikha River section, northwestern Siberian platform. Geological Magazine 144, 1–10.
. Sulphur and uranium isotope data are from carbonate-associated sulphate (δ34SCAS) and uranium (δ238UCAU), respectively. Age assignments derived from correlations to the carbon isotope stratigraphy and the age model of Maloof et al. (2010)Maloof, A.C., Porter, S.M., Moore, J.L., Dudas, F.O., Bowring, S.A., Higgins, J.A., Fike, D.A., Eddy, M.P. (2010) The earliest Cambrian record of animals and ocean geochemical change. Geological Society of America Bulletin 122, 1731–1774.
.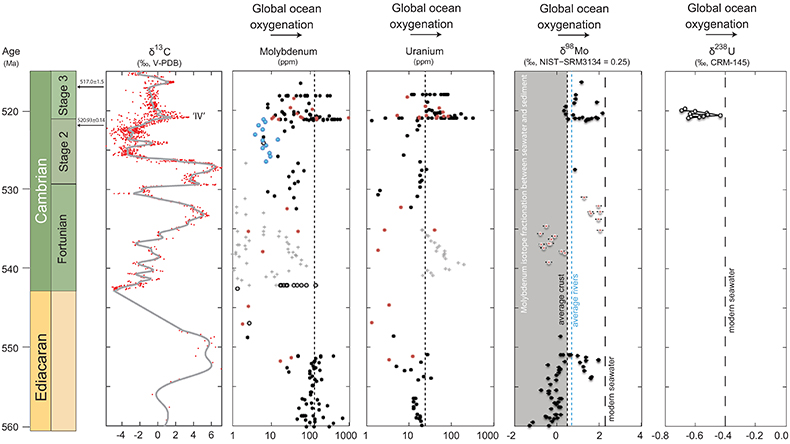
Figure 2 Summary of the redox proxy and carbon isotope data from latest Ediacaran to Early Cambrian (560–515 Myr). Redox proxy data includes the sedimentary contents and stable isotope compositions of molybdenum and uranium: Euxinic shales (black circles), Ferruginous shales (red circles), oxic shales (blue circles), shales from unknown redox environments (gray crosses), phosphorites (white diamonds), and carbonates (white circles). The grey field on the molybdenum isotope plot indicates values that are definitively fractionated from seawater, although values greater than these may be so as well. References for the data are listed in the Supplementary Information Extended Data, Table S-22.
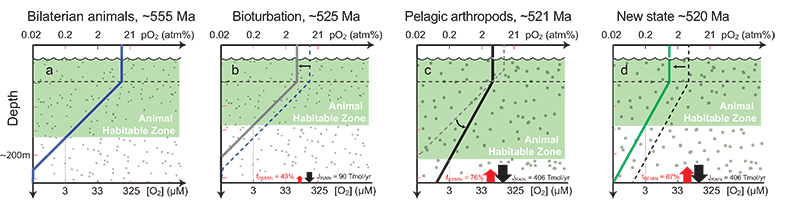
Figure 3 Conceptual model for the episodic expansion of the oxygenation zone in the oceans. The emergence of bilaterian animals (a-b) increased sediment mixing via bioturbation causing atmospheric pO2 to decline. The oxygenation zone contracts until (c) a rapid increase in the sinking rate of organic matter changes O2 consumption rates in the upper water column. (d) This accelerates organic carbon export to the sediments and delivers more food and O2 to the benthos over wider areas of the seafloor. Enhanced bioturbation promotes atmospheric pO2 decline, and re-stabilises the ocean in a more reducing state. Arrows and numbers illustrate organic export fluxes in one scenario (details in Table S-11). For simplicity, the organic C export increases in one step with the emergence of larger faecal pellets. Quantitative estimates for organic carbon export and remineralisation are derived from the coupled C and S isotope modelling (see Supplementary Information S5).
Back to article
Supplementary Figures and Tables
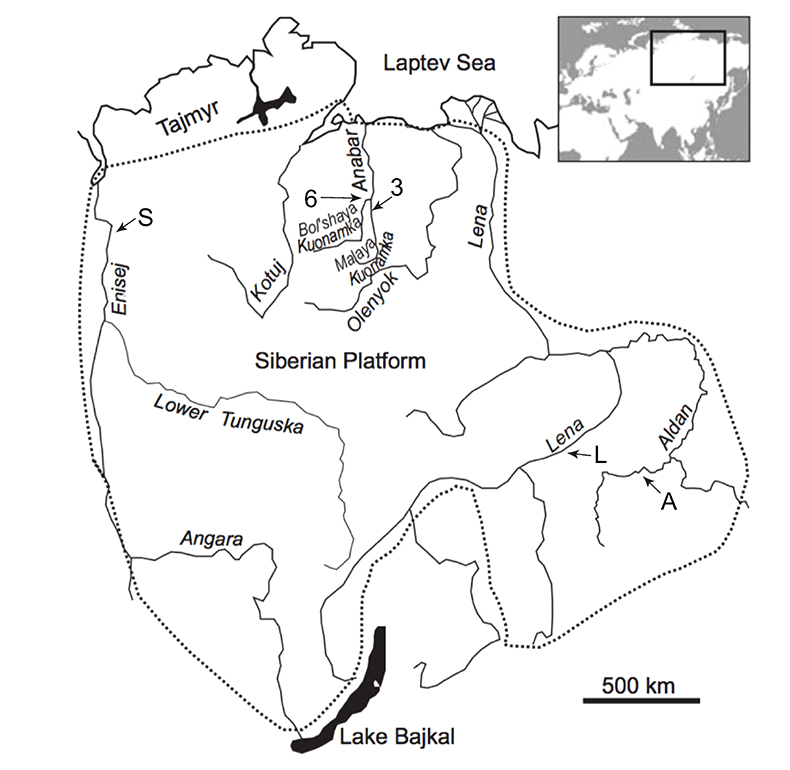
Figure S-1 Location of the studied sections Sukharikha (S), Bolshaya Kuonamka (6) and Malaya Kuonamka (3) and other sections at the Siberian platform discussed in the text (L–Middle Lena, A–Aldan Rivers).
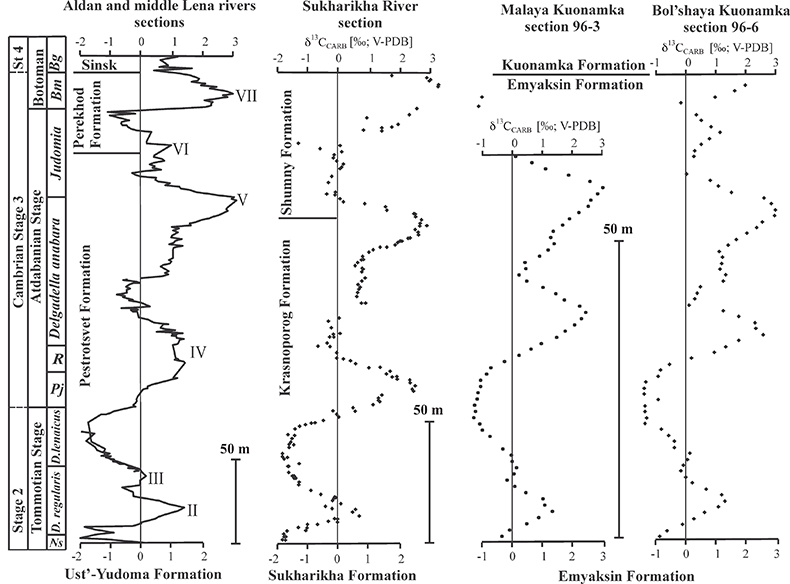
Figure S-2 Carbon isotope stratigraphy of the three studied sections and composite curve from Aldan and Middle Lena Rivers (Brasier et al., 1994; Kouchinsky et al., 2007). Zones as defined in the Lena-Aldan area: Ns – Nochoroicyathus sunnaginicus; D. regularis – Dokidocyathus regularis; D. lenaicus – Dokidocyathus lenaicus–Tumuliolynthus primigenius; Pj – Profallotaspis jakutensis; R – Repinaella; Bm – Bergeroniellus micmacciformis; Bg – Bergeroniellus gurarii.
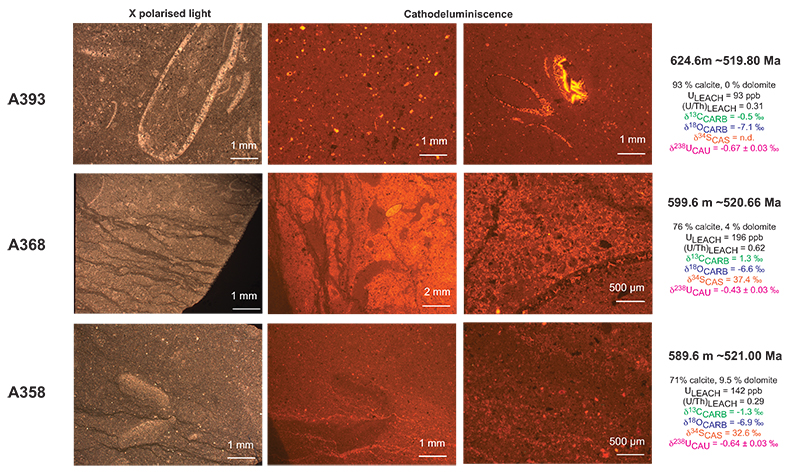
Figure S-3 Photomicrographs of samples (A358, A368 and A393) from the Sukharikha River section show microstructure and cathodoluminescent (CL) characteristics. Recrystallised shell fragments are embedded in a micrite matrix. Photographs are taken from thin section using multi-composite exposure (HDR). Selected geochemical data are summarised; n.d. – no data.
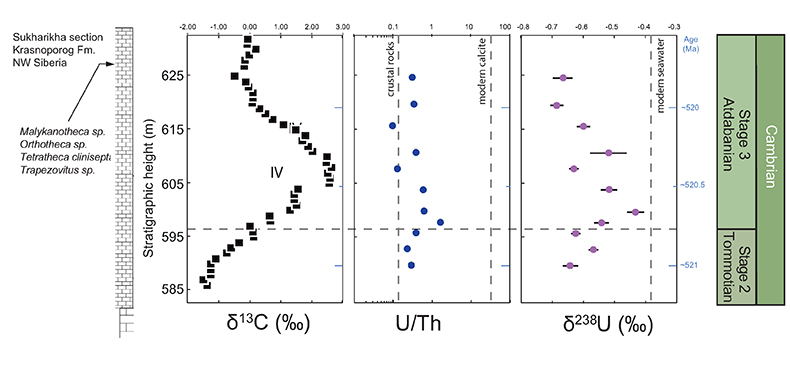
Figure S-4 Geochemical profiles from the Sukharikha River section showing δ13C, U/Th (note the logarithmic scale) and δ238U in stratigraphic context. The lithostratigraphy is adapted from Kouchinsky et al. (2007) and Rowland et al. (1998). The age assignment follows the model proposed by Maloof et al. (2010) assuming synchronicity worldwide in δ13C record tied to five absolute U/Pb age dates obtained from interbedded volcanic ashes in sections from Morocco (Maloof et al., 2010a). The uncertainty on δ13C is smaller than symbol size (2 SD reproducibility of samples from the same bed). The uncertainty of U/Th is <30 % measured on replicate leachates (see Extended Data 1). The uncertainty of δ238U is shown with error bars as 2 SE (replicate analyses of the same sample solution, see Table S-1).
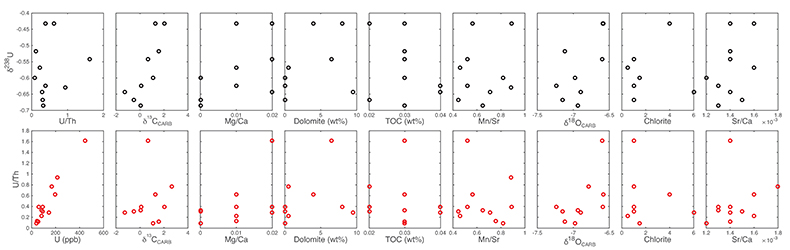
Figure S-5 Comparison of δ238U and highly reactive U to δ13C and geochemical indicators of dolomitisation (Mg/Ca, dolomite), pore water redox conditions (TOC), diagenetic alteration (Mn/Sr, δ18O), detrital input (Al/Ca, clay content), and primary carbonate mineralogy (Sr/Ca).
Table S-1 Pearson's correlation coefficients and p-values calculated to test the influence of diagenetic indicators on δ238U and U/Th. Uranium content (U) is linearly correlated to U/Th, hence the significance of the correlations between U and diagenetic indicators are similar. Statistical significant relationships are in bold (confidence interval = 5 %).
| R | p-value | |
| δ238U vs. U | 0.12 | 0.71 |
| δ238U vs. U/Th | 0.15 | 0.67 |
| U vs. U/Th | 0.96 | 8.11E-07 |
| δ238U vs. δ13C | 0.82 | 0.005 |
| δ238U vs. Mg/Ca | 0.52 | 0.15 |
| δ238U vs. TOC | -0.31 | 0.41 |
| δ238U vs. δ18O | 0.68 | 0.04 |
| δ238U vs. Mn/Sr | 0.14 | 0.69 |
| δ238U vs. Al/Ca | #N/D | #N/D |
| δ238U vs. Sr/Ca | 0.5 | 0.14 |
| δ238U vs. calcite | -0.66 | 0.07 |
| δ238U vs. quartz | 0.69 | 0.05 |
| δ238U vs. dolomite | 0.38 | 0.34 |
| δ238U vs. ankerite | -0.68 | 0.16 |
| δ238U vs. chlorite | 0.14 | 0.76 |
| δ238U vs. mica | 0.21 | 0.61 |
| δ238U vs. K-feldspar | 0.44 | 0.27 |
| U/Th vs. δ13C | 0.15 | 0.67 |
| U/Th vs. Mg/Ca | 0.49 | 0.15 |
| U/Th vs. TOC | -0.1 | 0.78 |
| U/Th vs. δ18O | 0.59 | 0.07 |
| U/Th vs. Mn/Sr | -0.13 | 0.71 |
| U/Th vs. Al/Ca | #N/D | #N/D |
| U/Th vs. Sr/Ca | 0.16 | 0.65 |
| U/Th vs. calcite | -0.13 | 0.75 |
| U/Th vs. quartz | 0.04 | 0.92 |
| U/Th vs. dolomite | 0.3 | 0.44 |
| U/Th vs. ankerite | -0.24 | 0.63 |
| U/Th vs. chlorite | 0.01 | 0.98 |
| U/Th vs. mica | -0.13 | 0.73 |
| U/Th vs. K-feldspar | 0.06 | 0.88 |
Table S-2 Uranium extracted from two reference materials with the sequential extraction procedure.
| U (ppb) | KTChalk | MCPhos |
| (100 % CaCO3) | (8.5 wt. % P2O5) | |
| 10 % acetic acid | 70 ± 4 | 440 ± 5 |
| 0.5 M HCl | 19 ± 1 | 872 ± 423 |
| 2 M HCl | 4 ± 0 | 133 ± 49 |
| HF + HNO3 | 14 ± 0 | 994 ± 8 |
| Total | 107 ± 4 | 2439 ± 426 |
Table S-3 Comparison of extraction yields for acetic acid vs. hydrochloric acid of various molarity.
| U | KTChalk | MCPhos |
| 10 % acetic acid | 75 ± 4 % | 30 ± 0 % |
| 0.5 M HCl | 20 ± 1 % | 60 ± 29 % |
| 2 M HCl | 4 ± 0 % | 9 ± 3 % |
| Total | 100 % | 100 % |
Table S-4 Repeated analyses of carbonate-associated U and δ238UCAU using the mild acetic acid extraction (with variable reaction time).
| Replicate | Reaction time | U (ppb) | δ238U (‰) |
| SRM-1d (modern argillaceous limestone) | |||
| #1 | 16 hr | 70 | –0.09 ± 0.02 |
| #2 | 16 hr | 743 | –0.08 ± 0.02 |
| #3 | 16 hr | 639 | –0.11 ± 0.02 |
| T1-13 (Cambrian limestone) | |||
| #3 | 30 min | 298 | –0.85 ± 0.02 |
| #4 | 4 hr | 292 | –0.83 ± 0.02 |
| #5 | 16 hr | 281 | –0.82 ± 0.03 |
| T1-26.5 (Cambrian limestone) | |||
| #1 | 16 hr | 102 | not determined |
| #2 | 16 hr | 155 | –0.56 ± 0.02 |
| #3 | 16 hr | 154 | –0.60 ± 0.03 |
Table S-5 Extraction yields for various mixtures of KTChalk and MCPhos.
| Acid | Chalk | 1:1† | 1:2ß | MCPhos | 1:1† | 1:2ß |
| measured | predicted | |||||
| 10 % acetic | 65 % | 35 % | 24 % | 18 % | 40 % | 33 % |
| 0.5 M HCl | 18 % | 37 % | 34 % | 36 % | 27 % | 30 % |
| 2 M HCl | 4 % | 5 % | 12 % | 5 % | 5 % | 5 % |
| HF + HNO3 | 13 % | 24 % | 3 % | 41 % | 28 % | 33 % |
†Mixing ratio 1:1 corresponds to 1.0187 g KTChalk (108 ng U) + 0.0519 g MCPhos (127 ng U).
ßMixing ratio 1:2 corresponds to 1.0993 g KTChalk (117 ng U) + 0.1138 g MCPhos (278 ng U).
Table S-6 Five parameterisations for the modern oceanic uranium isotope budget shown in Figure S-6. The models are broadly consistent with the modern ocean state.
| Case | 1 | 2 | 3 | 4 | 5 | 6 |
| Default | low δIN | hi ΔANOX | hi δIN | low ΔANOX | hi ΔOTHER | |
| δIN | –0.27 ‰ | –0.34 ‰ | –0.27 ‰ | –0.30 ‰ | –0.27 ‰ | –0.27 ‰ |
| ΔOTHER | 0.04 ‰ | 0.00 ‰ | 0.10 ‰ | 0.10 ‰ | 0.04 ‰ | 0.15 ‰ |
| ΔANOX | 0.50 ‰ | 0.50 ‰ | 0.60 ‰ | 0.60 ‰ | 0.40 ‰ | 0.40 ‰ |
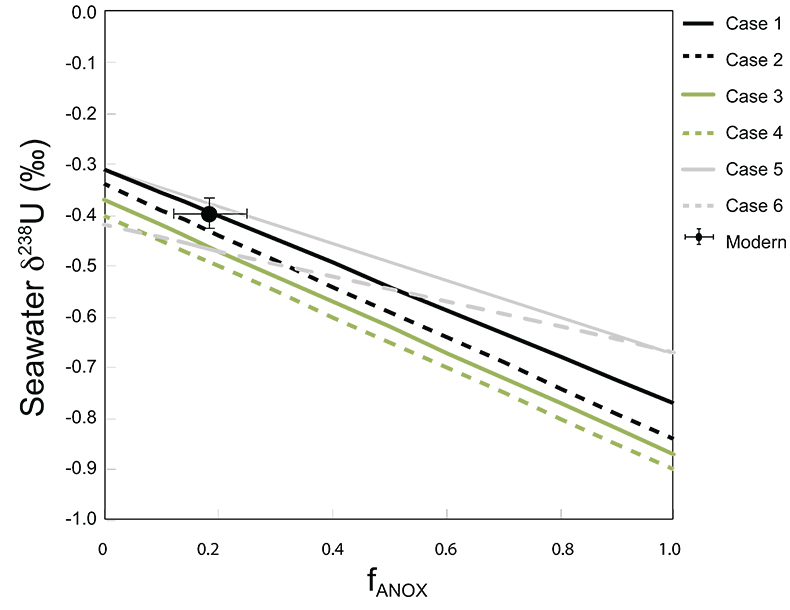
Figure S-6 Relationships between δSW and anoxic U burial fraction (fU) in the ocean are shown when the system is at steady state. The fraction of total oceanic U burial in anoxic basins (fU) is a key parameter that can shift seawater δ238U significantly below the modern value (black circle). The remaining U burial occurs in various oxygenated settings with a smaller isotopic imprint on global seawater (see text for details).
Table S-7 Parameter values used in the coupled Mo–U isotope mass balance models for today's ocean.
| Mo | U | |
| δIN | 0.7 | -0.27 |
| ΔOX | 2.8 | 0.04 |
| ΔANOX | 0.0 | 0.50 |
| ΔSAD | 1.4 | - |
| ƒOX | 30 % | 82 % |
| ƒSAD | 58 % | - |
| ƒEUX | 12 % | 18 % |
| Predicted δSW | 2.35 | -0.393 |
| Observed δSW | 2.34 ± 0.10 | -0.392 ± 0.005 |
(Note that all Δs are here defined positive, despite Mo and U isotope fractionations have opposite signs).
Back to article | Download in Excel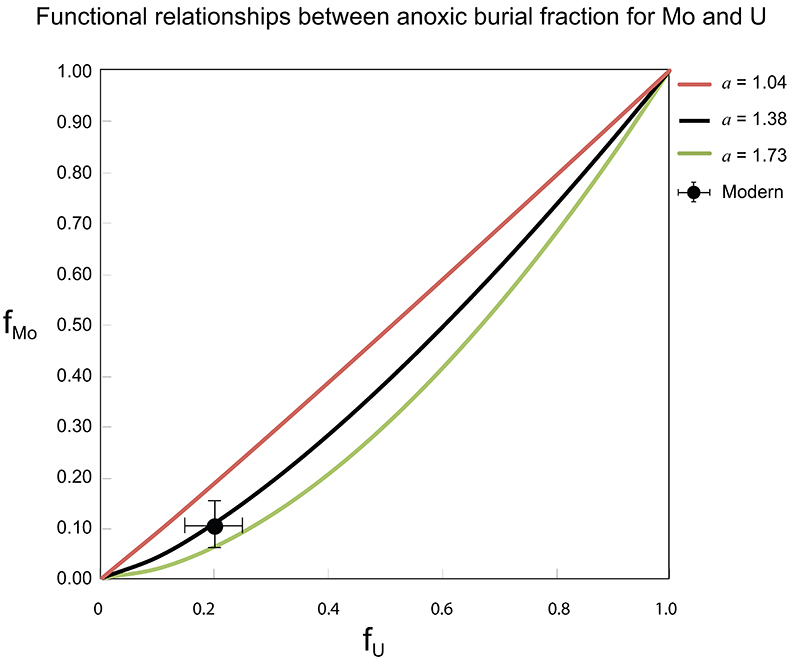
Figure S-7 Modelled functional relationships between euxinic Mo and U sinks. Modern estimates for the anoxic burial fractions (white square) suggest a is slightly larger than 1, consistent with modern oceanic budgets (Noordmann et al., 2016) where a = 1.38 ± 0.34.
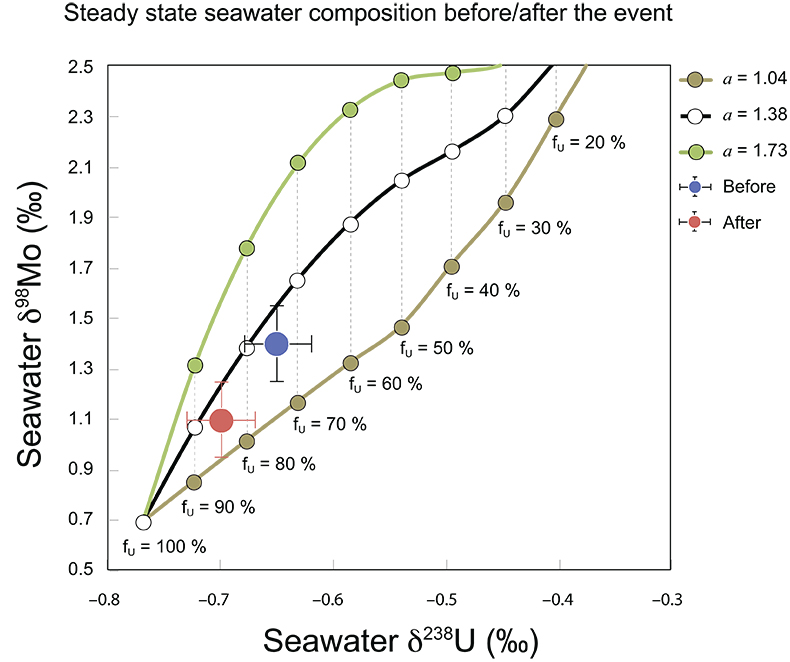
Figure S-8 Modelled seawater composition (δ238U, δ98Mo) for the early Cambrian steady states before and after the Cambrian Stage 2–3 event. The left most point represents 100 % burial in anoxic settings (fU = fMo = 1). At each step point towards the right, fU decreases 10 % (i.e. 90 %, 80 %, 70 %, etc.). The estimated composition of the δ238U and δ98Mo of early Cambrian seawater in ‰ before and after the event are (-0.65, -0.70) and (1.4, 1.1), respectively, Error bars show ±0.03 ‰ and ±0.15 for δ238U and δ98Mo, respectively.
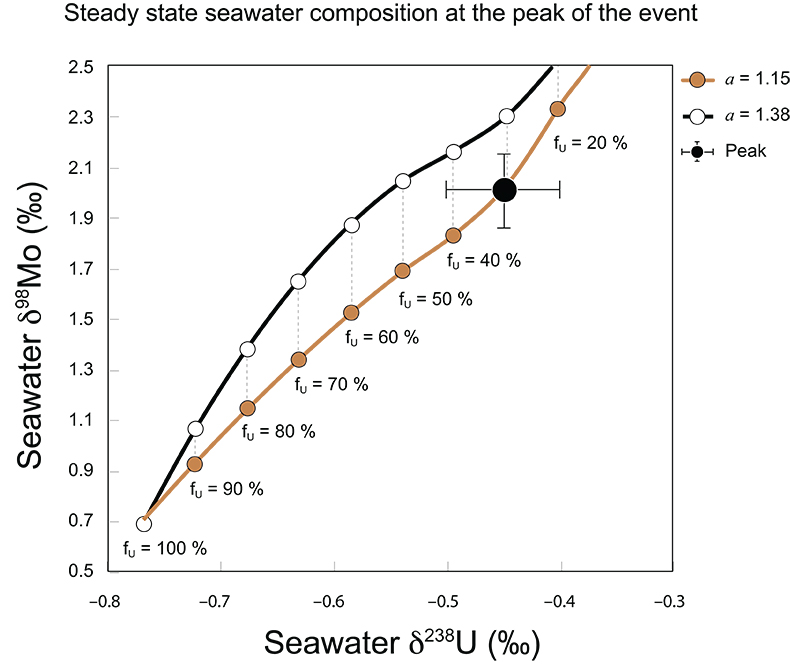
Figure S-9 The predicted composition of seawater at steady state for a = 1.15–1.38 is consistent with observations at the peak of the oxygenation event (δ238U = –0.45 ‰, δ98Mo = 2.0 ‰) with only 30 ± 10 % U removal into anoxic settings (corresponding to 25 ± 10 % and 19 ± 8 % Mo removal for a = 1.15 and 1.38, respectively).
Table S-8 Parameter values used for the C and S modelling.
| Modern alue | Explored range | Explanation | Ref | |
| α | 0.0072 | x (3-30) | Ratio of pyrite formation to organic carbon remineralisation rate | B07 |
| JRAIN | 192 · 1012 | ¥ | mol/yr. Modern organic rain rate | |
| JORG | 26 · 1012 | ¥ | mol/yr. Modern marine organic C burial rate | B07 |
| JLAND | 26 · 1012 | ß | mol/yr. Modern terrestrial organic C burial rate | |
| JEVAP | 2.1·1012 | x (0.2 - 1) | mol/yr. Cenozoic sulphate burial rate | CF09† |
| JCARB | 216·1012 | x (0.2 - 1) | mol/yr. Modern carbonate burial rate | BB12 |
| δIN.C | –5 ‰ | –5 ± 1 ‰ | δ13C of oceanic input | |
| ΔC | 26 ‰ | 24-30 ‰ | Average δ13C offset between seawater and buried organic matter | |
| δin.S | 8 ‰ | 4-16 ‰ | δ34S of oceanic input | |
| ΔS | 35 ‰ | 35-50 ‰ | Average δ34S offset between seawater and buried pyrite | |
| SR | 40 · 1012 | mol/yr. Modern organic burial rate | B07 | |
| SO42- | 28 | 2-3 | mM. Modern oceanic sulphate level | |
| JPY | 1.2 · 1012 | ¥ | mol/yr. Modern pyrite burial rate | B07 |
† The size of the modern oxidising C and S sinks were established from the isotope-derived f-constraints (Burdige, 2007; Saltzman and Thomas, 2012), suggesting ƒORG = 0.192 and ƒPY = 0.36 leads to steady state seawater values of δ13C = 0 ‰ and δ34S = 21 ‰, respectively. We assume that the modern terrestrial organic carbon burial equals that of marine organic carbon burial (Bergman et al., 2004), and neglect terrestrial pyrite burial.
¥ Model results are given in Tables S-9 to S-14
ß Terrestrial organic carbon burial (e.g., coal) is assumed equal to marine organic carbon (Bergman et al., 2004). Ref. B07 = Burdige (2007), Ref CF09 = Canfield and Farquhar (2009), Ref BB12 = Berner and Berner (2012).
Table S-9 Changes in the f-ratios during the Cambrian Stage 2–3 oxygenation episode. Uncertainties are propagated from the uncertainty of the isotope compositions of the inputs and the isotope fractionation associated with burial in reducing sinks (Table S-8)
| Before the event | At the peak | Behaviour | Modern value | |
| δC | 0 % | 3 % | increase | 0 ‰ |
| δS | 28 % | 40 % | increase | 21 ‰ |
| this leads to: | ||||
| ƒORG | 17 ± 4 % | 28 ± 5 % | increase | 20 ‰ |
| ƒPY | 40 ± 17 % | 70 ± 22 % | increase | 36 ‰ |
Table S-10 Ratios between reducing and oxidising sinks for carbon and sulphur changed during the Cambrian Stage 2–3 event.
| Before the event | At the peak | Behaviour | Modern value | |
| δ13C | 0 ‰ | 3 ‰ | increase | 0 ‰ |
| δ34S | 28 ‰ | 40 ‰ | increase | 21 ‰ |
| ƒORG /(1-ƒORG) | 0.21 ± 0.06 | 0.40 ± 0.10 | increase | 0.25 |
| ƒPY/(1-ƒPY) | 0.81 ± 0.51 | 6.21 ± 5.29 | increase | 0.56 |
Table S-11 Consequences for absolute organic carbon and pyrite sulphur flux, assuming modern-day values for JCARB, JEVAP, and α. The other constants are δIN, C = –5 ‰, δIN, S = 8 ‰, ΔS = 35 ‰, Δbio = 26 ‰. Flux unit: mol/yr.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 440·1012 | 3190·1012 | increase | 192 ·1012 |
| JORG | 52·1012 | 96·1012 | increase | 26 ·1012 |
| JPY | 2.8·1012 | 22·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.88 | 0.97 | increase | 0.87 |
Table S-12 Calculations with α = 0.070 (= 10 x modern). The higher α value leads to a solution with more modest organic load fluxes and less remineralisation, fREMIN < 0.76.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 90·1012 | 406·1012 | increase | 192 ·1012 |
| JORG | 50·1012 | 93·1012 | increase | 26 ·1012 |
| JPY | 2.8·1012 | 22·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.43 | 0.76 | increase | 0.87 |
Table S-13 Calculations with oxidative burial fluxes (JCARB, JEVAP) set at 1/4 of modern values. α set at 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 23·1012 | 100·1012 | increase | 192 ·1012 |
| JORG | 13·1012 | 24·1012 | increase | 26 ·1012 |
| JPY | 0.70·1012 | 5.6·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.43 | 0.76 | increase | 0.87 |
Table S-14 Calculations with ΔS set at 50 ‰ (as opposed to 35 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 69·1012 | 145·1012 | increase | 192 ·1012 |
| JORG | 50·1012 | 93·1012 | increase | 26 ·1012 |
| JPY | 1.4·1012 | 3.7·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.27 | 0.35 | increase | 0.87 |
Table S-15 Calculations with δIN,S set at 16 ‰ (as opposed to 8 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 67·1012 | 159 ·1012 | increase | 192 ·1012 |
| JORG | 50·1012 | 93 ·1012 | increase | 26 ·1012 |
| JPY | 1.1·1012 | 4.6 ·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.23 | 0.40 | increase | 0.87 |
Table S-16 Calculations with δIN,C set at –4 ‰ (as opposed to –5 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 71·1012 | 373·1012 | increase | 192 ·1012 |
| JORG | 31·1012 | 61·1012 | increase | 26 ·1012 |
| JPY | 2.8·1012 | 22·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.55 | 0.83 | increase | 0.87 |
Table S-17 Calculations with ΔBIO = 30 ‰ (as opposed to 26 ‰). α = 0.070.
| Before the event | At the peak | Behaviour | Modern value | |
| JRAIN | 82·1012 | 388·1012 | increase | 192 ·1012 |
| JORG | 42 ·1012 | 76 ·1012 | increase | 26 ·1012 |
| JPY | 2.8 ·1012 | 22 ·1012 | increase | 1.2 ·1012 |
| ƒREMIN | 0.47 | 0.80 | increase | 0.87 |
Table S-18 Summary of selected solutions and the increasing organic rain rate during the Cambrian Stage 2–3 event.
| Case | Example | Initial JRAIN | Increase of JRAIN | ƒREMIN |
| Modern oceans | 219·1012 | 87 % | ||
| 1 | Higher α (10-fold, α = 0.072) (Table S-12) | 90·1012 | x 4.5 | 43 to >76 % |
| 1b | Higher α (3-fold, α = 0.022) | 181·1012 | x 6.3 | 71 to >91 % |
| 1c | Higher α (30-fold, α = 0.22) | 64·1012 | x 3.1 | 20 to >52 % |
| 2 | Case 1 + smaller JCARB, JEVAP (1/5) (Table S-13) | 23·1012 | x 4.5 | 43 to >76 % |
| 3 | Case 1 + higher ΔS (50 ‰) (Table S-14) | 71·1012 | x 2.1 | 27 to >35 % |
| 4 | Case 1 + higher δIN,S (16 ‰) (Table S-15) | 67·1012 | x 2.4 | 23 to >40 % |
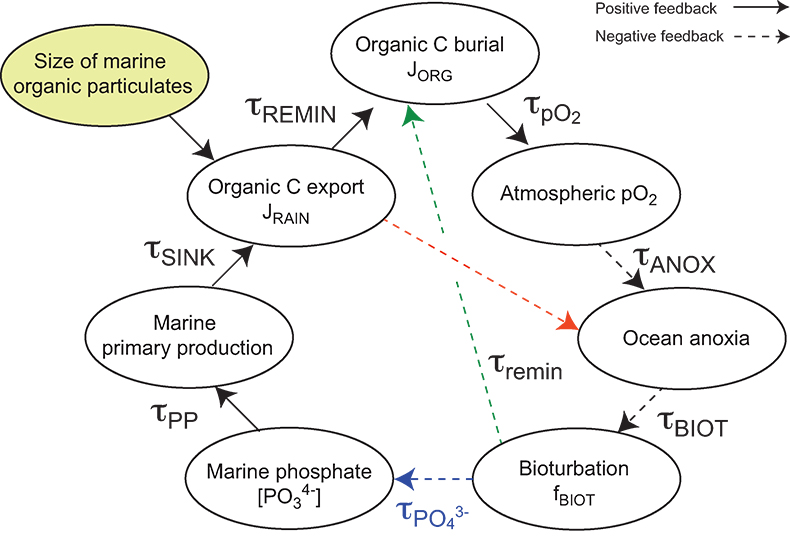
Figure S-10 Feedback diagram showing the oxygenation dynamics of the atmosphere-ocean system in response to increasing sinking rates of particulate organic matter in the oceans by larger animals with guts. See text for details.
Table S-19 Elemental and isotope data for samples from the Sukharikha River Section. Reference materials include IAPSO seawater, argillaceous limestone (SRM-1d), carbonatite (COQ-1) and Columbia River basalt (BCR-2). rpt = repeated analyses.
| Sample | Strat. height (m) | Age* (Ma) | Th (ppb) | U (ppb) | U/Th | δ238U (‰) | ± 2SE (‰) | n | U EFTh ƒ | Mg/Ca | Al/Ca | Fe/Ca | Mn/Sr | Sr/Ca |
| Sukharikha River Section (A), Krasnoporog Fm | ||||||||||||||
| A393 | 624.6 | 519.81 | 301 | 93 | 0.31 | -0.667 | 0.032 | 5 | 0.2 | 0 | 0 | 0 | 0.45 | 0.0015 |
| A388 | 619.6 | 519.98 | 249 | 83 | 0.33 | -0.686 | 0.021 | 5 | 0.3 | 0 | 0 | 0 | 0.65 | 0.0013 |
| A384 | 615.6 | 520.12 | 408 | 39 | 0.09 | -0.6 | 0.02 | 1 | -0.7 | 0 | 0 | 0 | 0.82 | 0.0012 |
| A379 | 610.6 | 520.29 | 155 | 60 | 0.39 | -0.433 | 0.043 | 5 | 0.5 | 0.02 | 0 | 0.01 | 0.89 | 0.0014 |
| A376 | 607.6 | 520.39 | 221 | 169 | 0.77 | 1.9 | 0.0018 | |||||||
| - rpt | 607.6 | 520.39 | 228 | 214 | 0.94 | -0.63 | 0.015 | 5 | 2.6 | 0.89 | ||||
| A372 | 603.6 | 520.53 | 449 | 54 | 0.12 | -0.517 | 0.026 | 3 | -0.5 | 0.0014 | ||||
| - rpt | 603.6 | 520.53 | 333 | 44 | 0.13 | -0.5 | 0.01 | 0 | 0.02 | 0.76 | ||||
| A368 | 599.6 | 520.66 | 317 | 196 | 0.62 | -0.432 | 0.027 | 5 | 1.4 | 0.01 | 0 | 0.01 | 0.56 | 0.0016 |
| A366 | 597.6 | 520.73 | 275 | 445 | 1.62 | -0.542 | 0.023 | 5 | 5.2 | 0.02 | 0 | 0.01 | 0.52 | 0.0014 |
| A364 | 595.6 | 520.8 | 231 | 90 | 0.39 | -0.625 | 0.015 | 5 | 0.5 | 0.01 | 0 | 0.01 | 0.52 | 0.0013 |
| A361 | 592.6 | 520.9 | 352 | 82 | 0.23 | -0.569 | 0.015 | 3 | -0.1 | 0.01 | 0 | 0.01 | 0.46 | 0.0016 |
| A358 | 589.6 | 521 | 487 | 142 | 0.29 | -0.643 | 0.025 | 5 | 0.1 | 0.02 | 0 | 0.02 | 0.71 | 0.0014 |
| Malaya Kuonamka River Section (K3), Emyaksin Fm | ||||||||||||||
| K3-18P | 21.5 | 521.4 | 268 | 120 | 0.45 | 0.7 | 0.03 | 0 | 0.02 | 1.52 | 0.0009 | |||
| K3-22P | 26 | 521.13 | 246 | 239 | 0.97 | 2.7 | 0.06 | 0 | 0.04 | 1.01 | 0.0014 | |||
| K3-26P | 30 | 520.89 | 456 | 54 | 0.12 | -0.5 | 0.03 | 0 | 0.02 | 2.12 | 0.0008 | |||
| K3-28P | 32 | 520.77 | 183 | 31 | 0.17 | -0.4 | 0.02 | 0 | 0.02 | 1.25 | 0.0011 | |||
| K3-30P | 34 | 520.65 | 310 | 54 | 0.17 | -0.3 | 0.05 | 0 | 0.03 | 1.38 | 0.0010 | |||
| K3-32P | 36 | 520.53 | 276 | 74 | 0.27 | 0.0 | 0.07 | 0 | 0.23 | 1.29 | 0.0014 | |||
| K3-35P | 39 | 520.35 | 418 | 49 | 0.12 | -0.6 | 0.02 | 0 | 0.02 | 0.74 | 0.0012 | |||
| K3-37P | 41 | 520.23 | 943 | 87 | 0.09 | -0.6 | 0.02 | 0 | 0.01 | 1.18 | 0.0009 | |||
| K3-39P | 43 | 520.11 | 338 | 34 | 0.10 | -0.6 | 0.02 | 0 | 0.02 | 1.29 | 0.0009 | |||
| K3-41P | 45 | 519.99 | 348 | 39 | 0.11 | -0.6 | 0.03 | 0 | 0.02 | 1.65 | 0.0010 | |||
| Bol'shaya Kuonamka (K6), Emyaksin Fm | ||||||||||||||
| K6-24 | 23 | 521.4 | 569 | 151 | 0.26 | 0.0 | 0.05 | 0 | 0.02 | 1.03 | 0.0012 | |||
| K6-27 | 26 | 521.15 | 363 | 67 | 0.19 | -0.3 | 0.04 | 0 | 0.02 | 1.44 | 0.0012 | |||
| K6-30 | 29 | 520.89 | 568 | 65 | 0.12 | -0.6 | 0.06 | 0.01 | 0.02 | 1.62 | 0.0011 | |||
| K6-31A | 30 | 520.81 | 615 | 137 | 0.22 | -0.1 | 0.02 | 0 | 0.02 | 0.98 | 0.0015 | |||
| K6-34 | 33 | 520.55 | 815 | 111 | 0.14 | -0.5 | 0.07 | 0 | 0.01 | 1.44 | 0.0013 | |||
| K6-35 | 34 | 520.47 | 475 | 72 | 0.15 | -0.4 | 0.02 | 0.01 | 0.01 | 0.97 | 0.0047 | |||
| K6-38 | 37 | 520.21 | 380 | 66 | 0.17 | -0.3 | 0.01 | 0 | 0.01 | 0.76 | 0.0009 | |||
| K6-39 | 38 | 520.13 | 312 | 46 | 0.15 | -0.4 | 0.01 | 0 | 0.02 | 1.35 | 0.0008 | |||
| K6-40 | 39 | 520.04 | 251 | 178 | 0.71 | 1.7 | 0.01 | 0 | 0 | 1.00 | 0.0009 | |||
| Reference materials | ||||||||||||||
| IAPSO seawater¬ | -0.342 | 0.022 | 5 | |||||||||||
| SRM-1d | 77 | 743 | 9.64 | -0.083 | 0.017 | 7 | 36.8 | 0.01 | 0.01 | 0.09 | ||||
| - rpt | 70 | 478 | 6.87 | -0.089 | 0.024 | 2 | 26.2 | 0 | 0 | 0 | ||||
| SRM-1d † | 5475 | 1475 | 0.27 | -0.105 | 0.017 | 7 | 1 | 0 | 0 | 0.01 | ||||
| COQ-1 † | 112 | 727 | 6.51 | -0.337 | 0.024 | 5 | 24.9 | 0.08 | 0.03 | 0.2 | ||||
| BCR-2 † | -0.274 | 0.017 | 5 | |||||||||||
| BCR-2 † | -0.255 | 0.013 | 4 | |||||||||||
| BCR-2 † | | | | | | -0.24 | 0.009 | 5 | ||||||
*Age model based on δ13C chemostratigraphy after Maloof et al. (2010a).
Samples marked with † are whole-rock analysis, all others are mild acetic leaches (see methods for details).
¬) The processing of IAPSO seawater followed the procedure of Weyer et al. (2008).
ƒ) Uranium Enrichment factor is calculated as follows: U EFTh = (U/Th) /(U/Th)UCC, where the UCC stands for upper continental crust with a U/Th = 0.26
Table S-20 Mineralogical data for samples from the Sukharikha River section.
| Sample | Calcite | Quartz | Dolomite | Ankerite | Chlorite (Clinochlore) | Mica | K-Feldspar | Haematite | sum |
| wt. % | wt. % | wt. % | wt. % | wt. % | wt. % | wt. % | wt. % | ||
| Sukharikha River Section. Igarka River. NW Siberia | |||||||||
| A393 | 93 | 2 | 0 | 1 | 1 | 3 | 100 | ||
| A388 | |||||||||
| A384 | 88 | 4 | 0 | 1.5 | 1.75 | 4.5 | 0.25 | 92 | |
| A379 | 56 | 25.5 | 8 | 0 | 2 | 8.5 | 66 | ||
| A376 | 85 | 11 | <5 | 0.5 | 1 | 0.5 | 2.5 | 97.5 | |
| A372 | |||||||||
| A368 | 76 | 7 | 4 | 2.5 | 4 | 2 | 4.5 | 95.5 | |
| A366 | 79 | 5 | 6.5 | 1.5 | 1 | 1 | 6 | 100 | |
| A364 | 90 | 5 | 0 | 1 | 0.5 | 3.5 | 96 | ||
| A361 | 90 | 2 | 0.5 | 0.5 | 0.5 | 1 | 5.5 | 94 | |
| A358 | 71 | 4 | 9.5 | 9.5 | 6 | 3 | 7.5 | 103 | |
| Bolshaya Kuonamka. Anabar Uplift. Section 96-6 | |||||||||
| K6-24 | 88 | 4 | 1.5 | 2 | 2.5 | 2 | 97.5 | ||
| K6-27 | 85 | 4 | 4 | 2.5 | 2 | 2 | 0.5 | 97 | |
| K6-30 | 80 | 4 | 8 | 3 | 2 | 2.5 | 0.5 | 97 | |
| K6-31A | 90 | 4 | 0.5 | 1 | 2 | 1.5 | 1.5 | < 0.5 | 97.5 |
| K6-31B | 86 | 4.5 | 0.5 | 1.5 | 2 | 2.5 | 2.5 | 0.5 | 90 |
| K6-34 | 76 | 5 | 3 | 6.5 | 3 | 2.5 | 3 | 1 | 97.5 |
| K6-35 | 82 | 5.5 | 3.5 | 2 | 2.5 | 2 | 2.5 | 89.5 | |
| K6-38 | 91 | 3 | 0.5 | 0.5 | 1 | 2 | 2 | 100 | |
| K6-39 | 87 | 4.5 | 1 | 1.5 | 2 | 2 | 2 | < 0.5 | 95.5 |
| K6-40 | 84 | 2 | | 0.5 | 1.5 | 1.5 | 0.5 | 86.5 | |
Table S-21 Sulphur isotope data of carbonate associated sulphate and total organic carbon content in samples from three Siberian sections (Sukharika River (A), Bolshaya Kuonamka river (K3), and Malaya Kuonamka river (K6)). Published C and O isotope data are shown for comparison (Kouchinsky et al., 2007).
| Sample | Age assigned | TOC | δ34S | δ13C | δ18O |
| Ma | wt. % | ‰ (V-CDT) | ‰ (V-PDB) | ‰ (V-PDB) | |
| Sukharikha River Section, Krasnoporog Fm | |||||
| A350 | 521.27 | 0.04 | 30.48 | -1.48 | -6.85 |
| A358 | 521 | 0.04 | 32.58 | -1.27 | -6.9 |
| A364 | 520.8 | 0.04 | 39.53 | 0.09 | -7.24 |
| A366 | 520.73 | 0.03 | 38.27 | 0.67 | -6.6 |
| A368 | 520.66 | 0.03 | 37.41 | 1.29 | -6.58 |
| A372 | 520.53 | 0.03 | 39.37 | 1.56 | -7.12 |
| A376 | 520.39 | 0.02 | 2.63 | -6.79 | |
| A379 | 520.29 | 0.02 | 37.5 | 2.03 | -6.59 |
| A384 | 520.12 | 0.03 | 1.09 | -6.98 | |
| A388 | 519.98 | 0.03 | 35.02 | 0.07 | -6.94 |
| A393 | 519.81 | 0.02 | -0.5 | -7.15 | |
| Malaya Kuonamka River Section (K3), Emyaksin Fm | |||||
| K3-18P | 521.4 | 0.033 | 27.93 | -1.29 | -6.24 |
| K3-22P | 521.13 | 0.159 | -1.1 | -5.78 | |
| K3-26P | 520.89 | 0.025 | 27.93 | -0.72 | -5.99 |
| K3-28P | 520.77 | 0.032 | 33.27 | 0.22 | -5.96 |
| K3-30P | 520.65 | 0.028 | 36.16 | 0.97 | -5.57 |
| K3-32P | 520.53 | 0.024 | 35.2 | 1.76 | -5.62 |
| K3-35P | 520.35 | 0.026 | 39.03 | 2.43 | -5.8 |
| K3-37P | 520.23 | 0.018 | 1.72 | -5.92 | |
| K3-39 | 520.11 | 0.027 | 1.03 | -5.88 | |
| K3-41 | 519.99 | 0.131 | 0.23 | -6.32 | |
| Bol'shaya Kuonamka (K6), Emyaksin Fm | |||||
| K6-24 | 521.4 | 0.046 | -1.22 | -6.01 | |
| K6-27 | 521.15 | 0.05 | 28.03 | -1.02 | -6.26 |
| K6-30 | 520.89 | 0.097 | 28.81 | -0.54 | -6.07 |
| K6-31 | 520.81 | 0.035 | 32.35 | 0.21 | -6.18 |
| K6-32 | 520.72 | 0.062 | 0.99 | -5.91 | |
| K6-34 | 520.55 | 0.041 | 36.86 | 1.8 | -5.42 |
| K6-35 | 520.47 | 0.1 | 2.63 | -5.49 | |
| K6-38 | 520.21 | 0.024 | 1.81 | -5.65 | |
| K6-39 | 520.13 | 0.095 | 34.93 | 1.27 | -5.84 |
| K6-40 | 520.04 | | | 0.11 | -5.95 |
Table S-22 Data sources for the marine redox proxy data (Mo, U, δ98Mo and δ238U) from Late Ediacaran and Cambrian sedimentary archives (modified after Boyle et al., 2014). All Mo isotope data were corrected from in-house reference materials to the NIST SRM 3136 scale (Goldberg et al., 2013; Nägler et al., 2014).
| Formation | Locality | Biozone | Lithology | Age (max) | Age (min) | Mo | U | Mo/TOC | U/TOC | δ98Mo | δ98Mo ref ‰ offset from NIST 3136 at 0.25 ‰ | References |
| Dictyonema Shales | Sweden | Shale | 482 | √ | Quinby-Hunt et al. (1989) | |||||||
| Alum Shale | Albjära, Sweden | Cambrian Series 4 | Shale | 485 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Alum Shale | Gislövhammar, Sweden | Cambrian Series 4 | Shale | 485 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Alum Shale | Cambrian Series 4 | Shale | 499 | √ | √ | Lewan and Buchardt (1989) | ||||||
| Alum Shale | Cambrian Series 4 | Shale | 499 | √ | √ | Partin et al. (2013) | ||||||
| Alum Shale | Andrarum-3, Sweden | Cambrian Series 3-4 | Shale | 500 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Alum Shale | Andrarum-3, Sweden | Cambrian Series 3-4 | Shale | 500 | √ | √ | √ | 0.08 | Gill et al. (2011) (except δ98Mo) | |||
| Alum Shale | Närke Area, Sweden | Shale | 505 | 499 | √ | √ | √ | Leventhal (1991) | ||||
| Burgess Shale | Canada | Cambrian Series 3 | Shale | 505 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Hay River | Georgina Basin, Australia | Shale | 505 | √ | √ | Donnelly et al. (1988) | ||||||
| Niutitang | Zunyi, South China | Cambrian Stage 3 | Shale | 520 | √ | √ | Jiang et al. (2006) | |||||
| Niutitang | Zhangjiajie | Cambrian Stage 3 | Shale | 520 | 520 | √ | √ | Jiang et al. (2006) | ||||
| Niutitang | Dingtai | Cambrian Stage 3 | Shale | 521 | 517 | √ | √ | √ | Xu et al. (2012) | |||
| Niutitang | Maluhe | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | Xu et al. (2012) | ||||
| Niutitang | Dazhuliushui | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | Xu et al. (2012) | ||||
| Niutitang | Sancha | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | Xu et al. (2012) | ||||
| Niutitang | Ganziping | Cambrian Stage 3 | Shale | 521 | 520 | √ | √ | √ | √ | Lehmann et al. (2007) | ||
| Niutitang | Yuanling | Cambrian Stage 3 | Shale | 521 | 520 | √ | √ | √ | √ | Lehmann et al. (2007) | ||
| Yuertushi | Xiaoerbulaki, Tarim Basin, NW China | Cambrian Stage 2 | Shale | 521 | √ | √ | √ | Yu et al. (2009) | ||||
| Yuertushi | Sugaitebulaki, Tarim Basin, NW China | Cambrian Stage 2 | Shale | 521 | √ | √ | Yu et al. (2009) | |||||
| Niutitang | Maluhe | Cambrian Stage 3 | Shale | 521 | √ | Lehmann et al. (2007) | ||||||
| Yu’anshan | Chengjiang, South China | Cambrian Stage 3 | Shale | 521 | √ | √ | √ | 0.08 | Dahl et al. (2010) | |||
| Niutitang | Ganziping | Cambrian Stage 3 | Shale | 521 | 520 | √ | Wille et al. (2008) | |||||
| Niutitang | Yuanling | Cambrian Stage 3 | Shale | 521 | 520 | √ | Wille et al. (2008) | |||||
| Yuanshan | Xiaotan, China | Cambrian Stage 3 | Shale | 521 | 518 | √ | √ | Och et al. (2013) | ||||
| Yuanshan | Dapotuo, China | Cambrian Stage 3 | Shale | 521 | 518 | √ | √ | Och et al. (2013) | ||||
| Niutitang | Zhongnan, China | Cambrian Stage 3 | Shale | 521 | 520 | √ | √ | Och et al. (2013) | ||||
| Niutitang | Dazhuliushui | Cambrian Stage 3 | Shale | 521 | √ | √ | Och et al. (2013) | |||||
| Niutitang | Maluhe | Cambrian Stage 3 | Shale | 521 | √ | √ | Och et al. (2013) | |||||
| Niutitang | Cili | Cambrian Stage 3 | Shale | 521 | √ | √ | Och et al. (2013) | |||||
| Guojiaba | Songtao section, South China | Cambrian Stage 2-3 | Shale | 524 | 508 | √ | √ | √ | √ | Guo et al. (2007) | ||
| Jiumenchong | Songtao section, South China | Cambrian Stage 2-3 | Shale | 524 | 520 | √ | √ | √ | √ | Guo et al. (2007) | ||
| Shiyantou | Meischucun, China | Cambrian Stage 2 | Shale | 524 | 522 | √ | √ | Och et al. (2013) | ||||
| Shiyantou | Dapotuo, China | Cambrian Stage 2 | Shale | 524 | 522 | √ | √ | Och et al. (2013) | ||||
| Shiyantou | Xiaotan, China | Cambrian Stage 2 | Shale | 529 | 521 | √ | √ | Och et al. (2013) | ||||
| Shiyantou | Meischucun, SYT | Cambrian Stage 2 | Shale | 529 | 521 | √ | √ | √ | Wen et al. (2011) | |||
| Hetang | Cambrian Stage 3 | Shale | 531 | √ | Zhou and Jiang (2009) | |||||||
| Ara Group | ALNR-1, Oman | Ediacaran-Cambrian | Shale | 540 | √ | √ | Wille et al. (2008) | |||||
| Ara Group | MM NW-1, Oman | Ediacaran-Cambrian | Shale | 540 | √ | √ | Wille et al. (2008) | |||||
| Ara Group | MM NW-1, Oman | Ediacaran-Cambrian | Shale | 542 | √ | Schröder and Grotzinger (2007) | ||||||
| Dengying | Ediacaran Series 2 | Shale | 545 | √ | Partin et al. (2013) | |||||||
| Dengying | Ediacaran Series 2 | Shale | 545 | √ | √ | Guo et al. (2007) | ||||||
| Liuchapo | Ediacaran Series 2 | Shale | 545 | √ | √ | Guo et al. (2007) | ||||||
| Dengying | Songtao section, South China | Shale | 545 | √ | Guo et al. (2007) | |||||||
| Nama Group | Namibia | Ediacaran Series 2 | Shale | 548 | √ | McLennan et al. (1983) | ||||||
| Doushantuo | Songtao section,South China | Shale | 551 | √ | Partin et al. (2013) | |||||||
| Doushantuo | Songtao section,South China | Shale | 551 | √ | Guo et al. (2007) | |||||||
| Isaac | Castle Creek + Cariboo Mountains, Windermere, Canada | Shale | 565 | √ | 0.08 | Dahl et al. (2010) | ||||||
| Drook | New Foundland, Canada | Shale | 565 | √ | √ | √ | 0.08 | Dahl et al. (2010) | ||||
| Doushantuo, Cycle 3 | Jiulongwan, Zhongling, Minle, Longe Nanhua Basin, South China | Shale | 565 | 555 | √ | √ | Li et al. (2010) | |||||
| Gaskiers | New Foundland, Canada | Shale | 580 | √ | √ | √ | 0.08 | Dahl et al. (2010) | ||||
| Upper Kaza | Windermere, Canada | | Shale | 580 | | √ | √ | √ | 0.08 | Dahl et al. (2010) |