Stable strontium isotopic heterogeneity in the solar system from double-spike data
Affiliations | Corresponding Author | Cite as | Funding information- Share this article





Article views:7,845Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract

Figures and Tables
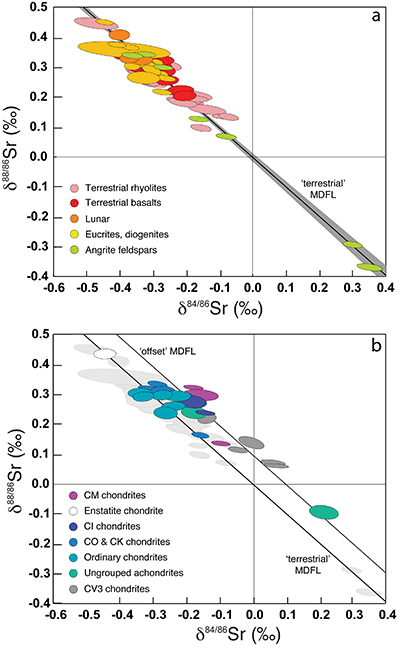 Figure 1 Three-isotope plots of all terrestrial and non-terrestrial data. (a) Plot of δ88/86Sr vs δ84/86Sr showing the data for terrestrial, lunar, eucrite, diogenite and angrite samples in this study (Supplementary Information, Table S-1). MDFL denotes the equilibrium mass-dependent fractionation line which passes through the origin (the assumed composition of NBS-987) with a slope of -0.978 (Young et al., 2002). The shaded region is the 2 s.d. error envelope around the line of best fit to the data points plotted; the line itself is analytically and visually indistinguishable from the equilibrium MDFL. Data points are represented by their 2 s.d. uncertainty envelopes calculated using the methods outlined in the Supplementary Information. (b) Plot of δ88/86Sr vs δ84/86Sr showing the data measured in this study. Data points plotted in panel a are greyed out to minimise overlap. We show two lines: a ‘terrestrial’ MDFL which is the line of best-fit to the data points shown in panel a, and an ‘offset’ MDFL calculated from ungrouped achondrites and chondrite classes CI, CV3 and CM2, together with the heavy end members of the CO and ordinary chondrite classes (see Table S-2 in Supplementary Information). | 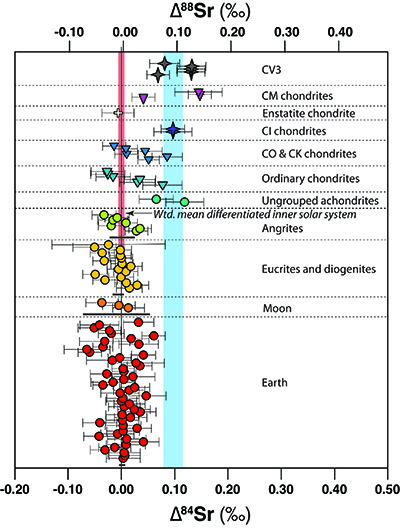 Figure 2 Plot of Δ84Sr and Δ88Sr for all samples (see Supplementary Information Table S-1 for data values). Uncertainties are 2 s.d., fully propagated (see Supplementary Information). Weighted mean values (±2 s.d.) for terrestrial, lunar, eucrite, diogenite and angrite samples are shown as horizontal grey bars for each of these data sets. The vertical pink bar extending through the ungrouped achondrite, ordinary chondrite and carbonaceous chondrite data is a weighted mean value (-0.0018 ± 0.0060, MSWD = 4.1) for the inner solar system derived from the terrestrial, lunar, eucrite, diogenite and angrite samples, and corresponds to the ‘terrestrial’ MDFL in Figure 1. The blue vertical line represents the weighted mean (±2 s.d) for the (largely undifferentiated) samples used to define the ‘offset’ MDFL (see text for details). |
| Figure 1 | Figure 2 |
Supplementary Figures and Tables
 Table S-1 Sample information and summary of Sr stable isotopic results for all samples used in this study, along with weighted means for each group of data. Details of correction for inter-batch bias, calculation of correlation coefficient and full propagation of uncertainties is given in the Supplementary Information. |  Table S-2 Sr isotopic compositions for the samples used for regression of the ‘offset’ MDFL in Figure 1b. | 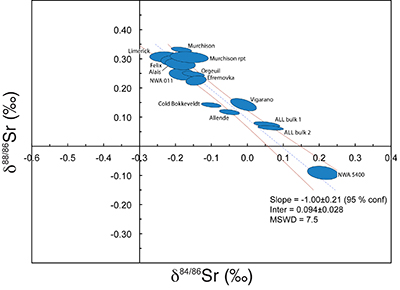 Figure S-1 Plot of δ88/86Sr vs. δ84/86Sr showing the data and best fit line and error envelope for the ‘offset’ MDFL shown in Figure 1b. |
| Table S-1 | Table S-2 | Figure S-1 |
top
Introduction
Isotopic anomalies in extraterrestrial materials hold the keys to disentangling the origins and development of the early solar system (Dauphas and Schauble, 2016
Dauphas, N., Schauble, E.A. (2016) Mass fractionation laws, mass-independent effects, and isotopic anomalies. Annual Review of Earth and Planetary Sciences 44, 709–783.
; Qin and Carlson, 2016Qin, L., Carlson, R.W. (2016) Nucleosynthetic isotope anomalies and their cosmochemical significance. Geochemical Journal 50, 43–65.
, for recent overviews). Stable strontium isotopes in particular are critical in discerning the nucleosynthetic origins of early solar system components and the timing of accretion processes. Furthermore, variations caused by high temperature mass-dependent fractionation (Young et al., 2002Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
) are also important (Patchett, 1980aPatchett, P.J. (1980a) Sr isotopic fractionation in Ca–Al inclusions from the Allende meteorite. Nature 283, 438–441.
,bPatchett, P.J. (1980b) Sr isotopic fractionation in Allende chondrules: a reflection of solar nebular processes. Earth and Planetary Science Letters 50, 181–188.
; Moynier et al., 2010Moynier, F., Agrainer, A., Hezel, D.C., Bouvier, A. (2010) Sr stable isotope composition of Earth, the Moon, Mars, Vesta and meteorites. Earth and Planetary Science Letters 300, 359–366.
; Charlier et al., 2012Charlier, B.L.A., Nowell, G.M., Parkinson, I.J., Kelley, S.P., Pearson, D.G., Burton, K.W. (2012) High temperature strontium stable isotope behaviour in the early solar system and planetary bodies. Earth and Planetary Science Letters 329–330, 31–40.
) in providing insights into nebular and accretionary processes.Disentangling strontium isotopic variations is problematic, however, through a first order analytical issue. Virtually all TIMS measurements of strontium isotopes employ a fixed 88Sr/86Sr ratio (8.375209) to correct for instrumental mass fractionation (IMF) during analysis (Papanastassiou and Wasserburg, 1969
Papanastassiou, D.A., Wasserburg, G.J. (1969) Initial strontium isotopic abundances and the resolution of small time differences in the formation of planetary bodies. Earth and Planetary Science Letters 5, 361–376.
, 1978Papanastassiou, D.A., Wasserburg, G.J. (1978) Strontium isotopic anomalies in the Allende meteorite. Geophysical Research Letters 5, 595–598.
; Moynier et al., 2010Moynier, F., Agrainer, A., Hezel, D.C., Bouvier, A. (2010) Sr stable isotope composition of Earth, the Moon, Mars, Vesta and meteorites. Earth and Planetary Science Letters 300, 359–366.
; Charlier et al., 2012Charlier, B.L.A., Nowell, G.M., Parkinson, I.J., Kelley, S.P., Pearson, D.G., Burton, K.W. (2012) High temperature strontium stable isotope behaviour in the early solar system and planetary bodies. Earth and Planetary Science Letters 329–330, 31–40.
; Hans et al., 2013Hans, U., Kleine, T., Bourdon, B. (2013) Rb–Sr chronology of volatile depletion in differentiated protoplanets: BABI, ADOR and ALL revisited. Earth and Planetary Science Letters 374, 204–214.
). However, adoption of this fixed value precludes investigation of mass-dependent variations in the stable isotopes. In comparison, MC-ICP-MS techniques using either Zr-normalisation and/or sample-standard bracketing (Moynier et al., 2010Moynier, F., Agrainer, A., Hezel, D.C., Bouvier, A. (2010) Sr stable isotope composition of Earth, the Moon, Mars, Vesta and meteorites. Earth and Planetary Science Letters 300, 359–366.
; Charlier et al., 2012Charlier, B.L.A., Nowell, G.M., Parkinson, I.J., Kelley, S.P., Pearson, D.G., Burton, K.W. (2012) High temperature strontium stable isotope behaviour in the early solar system and planetary bodies. Earth and Planetary Science Letters 329–330, 31–40.
) can yield 88Sr/86Sr and 87Sr/86Sr ratios to examine mass-dependent fractionation effects, but cannot accurately measure 84Sr/86Sr due to 84Kr interference. Most published Sr isotopic data are collectively hamstrung by one or other of these issues.Here we present TIMS data obtained using a double-spike methodology (Rudge et al., 2009
Rudge, J.F., Reynolds, B.C., Bourdon, B. (2009) The double spike toolbox. Chemical Geology 265, 420–431.
) that, in contrast, recovers the abundance of the four Sr isotopes, free from any normalisation assumption (see Supplementary Information). We have measured Sr isotopes in a suite of terrestrial, lunar, and undifferentiated and differentiated meteorite samples (Table S-1). We undertook two determinations on each sample: an unspiked measurement that is IMF-corrected and a spiked measurement which, in combination with the unspiked analysis, permits us to deconvolve the absolute ratios of 84Sr/86Sr, 88Sr/86Sr and 87Sr/86Sr, independent of any fixed IMF correction (Neymark et al., 2014Neymark, L.A., Premo, W.R., Mel’nikov, N.N., Emsbo, P. (2014) Precise determination of δ88Sr in rocks minerals and waters by double-spike TIMS: a powerful tool in the study of geological, hydrological and biological processes. Journal of Analytical Atomic Spectrometry 29, 65–75.
). Because the uncertainties associated with the values used to derive the isotopic ratios are highly correlated, we have also considered the individual errors associated with each measurement and propagated these to derive robust error estimates (Supplementary Information).top
Results and Discussion
Sr isotopic results from double spike data. We present our data in three-isotope plots (δ84/86Sr versus δ88/86Sr where δ represents ‰ deviation relative to NBS-987). Terrestrial samples (Fig. 1a) form a linear array that lies within error of the calculated equilibrium mass-dependent fractionation line (MDFL) produced by high temperature mass fractionation (Young et al., 2002
Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
), and cluster around the bulk silicate Earth value for δ88/86Sr of ~+0.29 ‰ (Moynier et al., 2010Moynier, F., Agrainer, A., Hezel, D.C., Bouvier, A. (2010) Sr stable isotope composition of Earth, the Moon, Mars, Vesta and meteorites. Earth and Planetary Science Letters 300, 359–366.
; Charlier et al., 2012Charlier, B.L.A., Nowell, G.M., Parkinson, I.J., Kelley, S.P., Pearson, D.G., Burton, K.W. (2012) High temperature strontium stable isotope behaviour in the early solar system and planetary bodies. Earth and Planetary Science Letters 329–330, 31–40.
). Linear regression on our data from all terrestrial, lunar, eucrite, diogenite, and angrite samples yields a line with a slope of -0.981 ± 0.047 (Mean Square of Weighted Deviation; MSWD = 4.1) that is identical within error to the theoretical equilibrium MDFL (slope = -0.978: Young et al., 2002Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
). Our regression line (here labelled the ‘terrestrial’ MDFL) passes within error of the origin, indicating that these samples and their parent bodies have a nucleosynthetic Sr isotopic composition in common with Earth (and the NBS987 standard, by definition), albeit modified by high temperature mass-dependent fractionation processes (see below). Other meteorite samples show contrasting behaviour, with variations in δ88/86Sr and/or δ84/86Sr, driving the data points away from the ‘terrestrial’ MDFL towards heavier values (Fig. 1b). Ungrouped achondrites and carbonaceous chondrites (classes CI, CV3, CM) lie significantly to the right of the ‘terrestrial’ MDFL. There can be defined an apparent second MDFL from the data for the ungrouped achondrites and chondrite classes CI, CV3 and CM, together with the heavy end members of the CO and CK classes (see Table S-1 for the samples used). This second line (labelled the ‘offset’ MDFL) has a slope of -1.00 ± 0.21; MSWD = 7.5. This ‘offset’ MDFL is displaced by 94 ± 28 ppm heavier in δ84/86Sr or δ88/86Sr from the ‘terrestrial’ MDFL (Fig. 1b). There is a spread in the data for the ordinary chondrites and CO and CK undifferentiated samples between the two MDFLs: these data are plotted in Figure 1b, but not used to define the offset MDFL.
Figure 1 Three-isotope plots of all terrestrial and non-terrestrial data. (a) Plot of δ88/86Sr vs δ84/86Sr showing the data for terrestrial, lunar, eucrite, diogenite and angrite samples in this study (Supplementary Information, Table S-1). MDFL denotes the equilibrium mass-dependent fractionation line which passes through the origin (the assumed composition of NBS-987) with a slope of -0.978 (Young et al., 2002
Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
). The shaded region is the 2 s.d. error envelope around the line of best fit to the data points plotted; the line itself is analytically and visually indistinguishable from the equilibrium MDFL. Data points are represented by their 2 s.d. uncertainty envelopes calculated using the methods outlined in the Supplementary Information. (b) Plot of δ88/86Sr vs δ84/86Sr showing the data measured in this study. Data points plotted in panel a are greyed out to minimise overlap. We show two lines: a ‘terrestrial’ MDFL which is the line of best-fit to the data points shown in panel a, and an ‘offset’ MDFL calculated from ungrouped achondrites and chondrite classes CI, CV3 and CM2, together with the heavy end members of the CO and ordinary chondrite classes (see Table S-2 in Supplementary Information).In general, the ‘terrestrial’ and ‘offset’ MDFLs are defined by differentiated versus undifferentiated materials, respectively. However, there are three exceptions to this generalisation. First, the enstatite chondrite (Abee) lies exactly on the ‘terrestrial’ line, despite its undifferentiated nature. Second, and in contrast, the two anomalous achondrites (NWA 011, NWA 5400) both lie within error of the ‘offset’ MDFL despite their differentiated nature. NWA 011 similarly plots within the ‘carbonaceous chondrite’ field in Cr-Ti isotopic space (see Warren, 2011
Warren, P.H. (2011) Stable-isotopic anomalies and the accretionary assemblage of the Earth and mars: a subordinate role for carbonaceous chondrites. Earth and Planetary Science Letters 311, 93–100.
). Third, the diversity seen in the ordinary chondrites and CO and CK undifferentiated samples we infer reflects the mixing within individual samples between components that have been through some kind of processing (falling on the ‘terrestrial’ MDFL) versus those not processed (falling on the ‘offset’ MDFL). Analysis of individual, physically separated components from these meteorites would be needed to test this inference.Mass-dependent fractionation processes. From our work we can evaluate unambiguously the extent of mass-dependent Sr isotopic fractionation within the various reservoirs contributing to planetary materials. This can only be achieved through use of the double-spike technique. Equilibrium or kinetic fractionation effects (e.g., Blanchard et al., 2017
Blanchard, M., Balan, E., Schauble, E.A. (2017) Equilibrium fractionation of non-traditional stable isotopes: a molecular modeling perspective. Reviews in Mineralogy and Geochemistry 82, 27–63.
; Watkins et al., 2017Watkins, J.M., DePaolo, D.J., Watson, E.B. (2017) Kinetic fractionation of non-traditional stable isotopes by diffusion and crystal growth reactions. Reviews in Mineralogy and Geochemistry 82, 85–125.
) in the data presented here can be related to two different realms of processes. First, the fractionation that occurred during the development of the components that were assembled to produce the meteorites (regardless of their degree of differentiation). Second, magmatic processes leading to differentiation in newly forming and present-day planetary objects. The influence of ‘normal’ magmatic processes is seen in the spread in values along the MDFL shown by our terrestrial samples where they cover a range about half that of the entire sample suite.Mass-independent anomalies. To allow for mass-dependent fractionation and highlight the anomalies due to either p-process 84Sr or r-process-influenced 88Sr, we recast our data as ∆ values, i.e. the difference between the true value and the corresponding value along the equilibrium MDFL calculated using the true value for the other isotopic ratio (Fig. 2). If the anomalies are due solely to 84Sr, the departure from the MDFL is horizontal in Figure 1, whereas if the anomaly is solely in 88Sr, the offset is vertical. In practice, the numerical values for ∆84Sr and ∆88Sr so calculated are virtually identical because the MDFL slope is so close to 45º and the line is effectively straight across the range of values reported here. Comparison of our results with published data shows several features. The weighted mean ∆84Sr of our terrestrial samples (assuming that any variation is in 84Sr alone) is -0.0002 ± 0.0083 ‰ 2 s.d. (MSWD = 4.3, n = 51), and that of the terrestrial, lunar, eucrite, diogenite and angrite feldspar samples combined is -0.0018 ± 0.0060 ‰ 2 s.d. (MSWD = 4.1, n = 78), demonstrating that the NBS-987 84Sr/86Sr composition is not at all anomalous (cf. Moynier et al., 2012
Moynier, F., Day, J.M.D., Okui, W., Yokoyama, T., Bouvier, A., Walker, R.J., Podosek, F.A. (2012) Planetary-scale strontium isotopic heterogeneity and the age of volatile depletion of early solar system materials. Astrophysical Journal 758, 45.
). Additionally, differences in 84Sr/86Sr proposed between Earth, Moon and enstatite chondrites versus eucrites and ordinary chondrites (Moynier et al., 2012Moynier, F., Day, J.M.D., Okui, W., Yokoyama, T., Bouvier, A., Walker, R.J., Podosek, F.A. (2012) Planetary-scale strontium isotopic heterogeneity and the age of volatile depletion of early solar system materials. Astrophysical Journal 758, 45.
) are not seen in our results. It is not clear how such discrepancies have arisen.If the non-mass-dependent anomalies that we report are considered as reflecting p-process variations in 84Sr, then several conclusions can be drawn. The elevated apparent ∆84Sr values we obtain from bulk samples in CI, CV and CM chondrites (Fig. 2) cannot reflect incomplete dissolution of refractory pre-solar SiC grains, with their highly depleted 84Sr (Nicolussi et al., 1998
Nicolussi, G.K., Pellin, M.J., Lewis, R.S., Davis, A.M., Clayton, R.N., Amari, S. (1998) Strontium isotopic composition in individual circumstellar silicon carbide grains: a record of s-process nucleosynthesis. Physical Review Letters 81, 3583–3586.
; Podosek et al., 2004Podosek, F., Prombo, C., Amari, S., Lewis, R. (2004) s-process Sr isotopic compositions in presolar SiC from the Murchison meteorite. Astrophysical Journal 605, 960–965.
; Paton et al., 2013Paton, C., Schiller, M., Bizzarro, M. (2013) Identification of an 84Sr-depleted carrier in primitive meteorites and implications for thermal processing in the solar protoplanetary disk. Astrophysical Journal Letters 763, L40.
), as such grains are not present in concentrations that would significantly affect the bulk meteorite composition (Moynier et al., 2012Moynier, F., Day, J.M.D., Okui, W., Yokoyama, T., Bouvier, A., Walker, R.J., Podosek, F.A. (2012) Planetary-scale strontium isotopic heterogeneity and the age of volatile depletion of early solar system materials. Astrophysical Journal 758, 45.
; Paton et al., 2013Paton, C., Schiller, M., Bizzarro, M. (2013) Identification of an 84Sr-depleted carrier in primitive meteorites and implications for thermal processing in the solar protoplanetary disk. Astrophysical Journal Letters 763, L40.
). CV3 chondrites contain less SiC than CM chondrites (Huss et al., 2003Huss, G.R., Meshik, A.P., Smith, J.B., Hohenberg, C.M. (2003) Presolar diamond, silicon carbide, and graphite in carbonaceous chondrites: implications for thermal processing in the solar nebula. Geochimica et Cosmochimica Acta 67, 4823–4848.
), yet we record a similar range in elevated apparent ∆84Sr values. Two dissolutions of Murchison from separate chips of this stone also yield apparent ∆84Sr values that are in close agreement. Moreover, the elevated apparent ∆84Sr values in two ungrouped achondrite samples (Fig. 1b; Supplementary Information, Table S-1) reflect the bulk composition since these differentiated stones are unlikely to contain any surviving pre-solar material (Dauphas and Schauble, 2016Dauphas, N., Schauble, E.A. (2016) Mass fractionation laws, mass-independent effects, and isotopic anomalies. Annual Review of Earth and Planetary Sciences 44, 709–783.
).
Figure 2 Plot of Δ84Sr and Δ88Sr for all samples (see Supplementary Information Table S-1 for data values). Uncertainties are 2 s.d., fully propagated (see Supplementary Information). Weighted mean values (±2 s.d.) for terrestrial, lunar, eucrite, diogenite and angrite samples are shown as horizontal grey bars for each of these data sets. The vertical pink bar extending through the ungrouped achondrite, ordinary chondrite and carbonaceous chondrite data is a weighted mean value (-0.0018 ± 0.0060, MSWD = 4.1) for the inner solar system derived from the terrestrial, lunar, eucrite, diogenite and angrite samples, and corresponds to the ‘terrestrial’ MDFL in Figure 1. The blue vertical line represents the weighted mean (±2 s.d) for the (largely undifferentiated) samples used to define the ‘offset’ MDFL (see text for details).
84Sr or 88Sr anomalies?: testing for p- versus r-process anomalies in Sr. As an inescapable consequence of the number of isotopes available, there are two contrasting (but not mutually exclusive) possibilities for the origins of the non-mass-dependent behaviour in Sr: anomalies in p-process 84Sr (e.g., Moynier et al., 2012
Moynier, F., Day, J.M.D., Okui, W., Yokoyama, T., Bouvier, A., Walker, R.J., Podosek, F.A. (2012) Planetary-scale strontium isotopic heterogeneity and the age of volatile depletion of early solar system materials. Astrophysical Journal 758, 45.
) and/or in r-(plus s-)process 88Sr (e.g., Qin and Carlson, 2016Qin, L., Carlson, R.W. (2016) Nucleosynthetic isotope anomalies and their cosmochemical significance. Geochemical Journal 50, 43–65.
). If the radiogenic contribution to 87Sr can be accurately determined, then three-isotope plots of (87Sr/86Sr)i versus δ84/86Sr and δ88/86Sr should show in their deviations from a single MDFL which of the isotopes is anomalous, since the 87Sr/86Sr ratio generated by double-spike techniques will also reflect mass-dependent fractionation processes (Neymark et al., 2014Neymark, L.A., Premo, W.R., Mel’nikov, N.N., Emsbo, P. (2014) Precise determination of δ88Sr in rocks minerals and waters by double-spike TIMS: a powerful tool in the study of geological, hydrological and biological processes. Journal of Analytical Atomic Spectrometry 29, 65–75.
). The key to resolving the source of the anomalies therefore lies in determining the initial 87Sr/86Sr characteristics of the relevant materials, both without the effects of radiogenic ingrowth and accounting for mass-dependent effects. The data need to be acquired using TIMS double-spike techniques because of the requirement that the δ84/86Sr ratio also needs to be accurately known in order to constrain the mass-dependent fractionation for all the Sr isotope ratios. Additionally, what is required is a suite of materials where the initial 87Rb/86Sr ratio was extremely low through formation from volatile element depleted materials (either during the initial condensation, or crystallisation from a volatile depleted melt), and any Rb present has remained undisturbed by further processing or secondary alteration. In addition, the discrimination between p- and r-process anomalies could be addressed through consideration of other isotope systems, such as Mo, Ba or Sm (e.g., Brennecka et al., 2013Brennecka, G.A., Borg, L.E., Wadhwa, M. (2013) Evidence for supernova injection into the solar nebula and the decoupling of r-process nucleosynthesis. Proceedings of the National Academy of Science, USA 110, 17241–17246.
). However, the relevant data must be obtained from an aliquot of the same dissolution as that used for the Sr isotopic analysis to avoid issues with sample heterogeneity.The two part nature of the early solar system. Our data are consistent with previous proposals for a primary division between the materials represented by almost entirely undifferentiated, carbonaceous meteorites from the outer solar system, versus (almost invariably) differentiated, non-carbonaceous materials from the inner solar system (Warren, 2011
Warren, P.H. (2011) Stable-isotopic anomalies and the accretionary assemblage of the Earth and mars: a subordinate role for carbonaceous chondrites. Earth and Planetary Science Letters 311, 93–100.
; Kruijer et al., 2017Kruijer, T.S., Burkhardt, C., Budde, G., Kleine, T. (2017) Age of Jupiter inferred from the distinct genetics and formation times of meteorites. Proceedings of the National Academy of Science, USA 114, 6712–6716.
). This division is shown, for example, in Cr and Ti (e.g., Trinquier et al., 2009Trinquier A., Elliott, T., Ulfbeck, D., Coath, C., Krot, A.N., Bizzarro, M. (2009) Origin of nucleosynthetic isotope heterogeneity in the solar protoplanetary disc. Science 324, 374–376.
) and Mo and W (e.g., Burkhardt et al., 2012Burkhardt, C., Kleine, T., Dauphas, N, Weiler, R. (2012) Origin of isotopic heterogeneity in the solar nebula by thermal processing and mixing of nebular dust. Earth and Planetary Science Letters 357–358, 298–307.
) and in our data is represented by our dual, effectively parallel MDFLs (Fig. 1a,b). Note, however, that some differentiated meteorites isotopically group with the other undifferentiated samples (Tables S-1 and S-2, Figure S-1), such as NWA011 (Warren, 2011Warren, P.H. (2011) Stable-isotopic anomalies and the accretionary assemblage of the Earth and mars: a subordinate role for carbonaceous chondrites. Earth and Planetary Science Letters 311, 93–100.
) and NWA 5400 (Burkhardt et al., 2017Burkhardt, C., Dauphas, N., Tang, H., Fischer-Godde, M., Qin, L., Chen, J., Rout, S., Pack, A., Heck, P., Papanastassiou, D. (2017) In search of the Earth-forming reservoir: Mineralogical, chemical, and isotopic characterizations of the ungrouped achondrite NWA 5363/NWA 5400 and selected chondrites. Meteoritics and Planetary Science 52, 807–826.
). In turn, our enstatite chondrite sample, although undifferentiated, falls along the terrestrial MDFL as do the lighter end members of the ordinary, CO and CM chondrites (Fig. 1a,b). Kruijer et al. (2017)Kruijer, T.S., Burkhardt, C., Budde, G., Kleine, T. (2017) Age of Jupiter inferred from the distinct genetics and formation times of meteorites. Proceedings of the National Academy of Science, USA 114, 6712–6716.
in their proposal for a distinct contrast between inner and outer solar system domains for early-formed objects point out that differentiation sufficient to start the processes of metal separation and core formation occurred also in the outer domain. It is thus not surprising that some differentiated meteorites plot in their isotopic characteristics with the typical undifferentiated suite of materials.The data variations that can be attributed to mass-dependent processes (i.e. the elongation of the data along the MDFL: Fig. 1) in turn have important implications for two aspects of early solar system history. First, our data indicate that high temperature processes have produced resolvable mass-dependent fractionation in materials that have gone to form many of the meteorite classes (both differentiated and undifferentiated) as well as within the terrestrial and lunar materials (cf. Simon and DePaolo, 2010
Simon, J.I., DePaolo, D.J. (2010) Stable calcium isotopic composition of meteorites and rocky planets. Earth and Planetary Science Letters 289, 457–466.
). Second, contrasting interpretations (e.g., Papanastassiou and Wasserburg, 1969Papanastassiou, D.A., Wasserburg, G.J. (1969) Initial strontium isotopic abundances and the resolution of small time differences in the formation of planetary bodies. Earth and Planetary Science Letters 5, 361–376.
; Halliday and Porcelli, 2001Halliday, A.N., Porcelli, D. (2001) In search of lost planets – the paleocosmochemistry of the inner solar system. Earth and Planetary Science Letters 192, 545–559.
; Hans et al., 2013Hans, U., Kleine, T., Bourdon, B. (2013) Rb–Sr chronology of volatile depletion in differentiated protoplanets: BABI, ADOR and ALL revisited. Earth and Planetary Science Letters 374, 204–214.
) of the disparities in initial 87Sr/86Sr ratios in BABI, Angra dos Reis and Allende should be reconsidered. We suggest that fractionation processes (both mass-dependent and mass-independent) prior to radiogenic 87Sr ingrowth must be considered as possible contributors to these disparities, rather than them simply reflecting age differences related to the timing of volatile element depletion. Also, if there is any r-process anomaly in 88Sr, then the initial 87Sr/86Sr value is subject to the inaccuracy in any internally normalised data that employs a fixed 88Sr/86Sr ratio for IMF corrections.Adoption of double-spike techniques is thus central to unlocking accurate, precise measurements and modelling of early solar system processes using Sr isotopes. The unique insights given by double-spike data open up new perspectives on the links between early solar system bodies, illuminating the different contributions to Sr isotopic variability from nucleosynthetic and variably coupled mass-dependent fractionation processes.
top
Acknowledgements
The CEPSAR isotope laboratories were supported by The Open University and NERC. We thank Sam Hammond and Manuela Fehr for help in the geochemistry laboratories, Caroline Smith (NHM, London) for samples and two anonymous reviewers for their helpful comments. Graphical abstract image credit: Victoria University of Wellington.
Editor: Bruce Watson
top
References
Blanchard, M., Balan, E., Schauble, E.A. (2017) Equilibrium fractionation of non-traditional stable isotopes: a molecular modeling perspective. Reviews in Mineralogy and Geochemistry 82, 27–63.
 Show in context
Show in context Equilibrium or kinetic fractionation effects (e.g., Blanchard et al., 2017; Watkins et al., 2017) in the data presented here can be related to two different realms of processes.
View in article
Brennecka, G.A., Borg, L.E., Wadhwa, M. (2013) Evidence for supernova injection into the solar nebula and the decoupling of r-process nucleosynthesis. Proceedings of the National Academy of Science, USA 110, 17241–17246.
 Show in context
Show in context In addition, the discrimination between p- and r-process anomalies could be addressed through consideration of other isotope systems, such as Mo, Ba or Sm (e.g., Brennecka et al., 2013).
View in article
Burkhardt, C., Kleine, T., Dauphas, N, Weiler, R. (2012) Origin of isotopic heterogeneity in the solar nebula by thermal processing and mixing of nebular dust. Earth and Planetary Science Letters 357–358, 298–307.
 Show in context
Show in context This division is shown, for example, in Cr and Ti (e.g., Trinquier et al., 2009) and Mo and W (e.g., Burkhardt et al., 2012) and in our data is represented by our dual, effectively parallel MDFLs (Fig. 1a,b).
View in article
Burkhardt, C., Dauphas, N., Tang, H., Fischer-Godde, M., Qin, L., Chen, J., Rout, S., Pack, A., Heck, P., Papanastassiou, D. (2017) In search of the Earth-forming reservoir: Mineralogical, chemical, and isotopic characterizations of the ungrouped achondrite NWA 5363/NWA 5400 and selected chondrites. Meteoritics and Planetary Science 52, 807–826.
 Show in context
Show in context Note, however, that some differentiated meteorites isotopically group with the other undifferentiated samples (Tables S-1 and S-2, Figure S-1), such as NWA011 (Warren, 2011) and NWA 5400 (Burkhardt et al., 2017).
View in article
Charlier, B.L.A., Nowell, G.M., Parkinson, I.J., Kelley, S.P., Pearson, D.G., Burton, K.W. (2012) High temperature strontium stable isotope behaviour in the early solar system and planetary bodies. Earth and Planetary Science Letters 329–330, 31–40.
 Show in context
Show in contextFurthermore, variations caused by high temperature mass-dependent fractionation (Young et al., 2002) are also important (Patchett, 1980a,b; Moynier et al., 2010; Charlier et al., 2012) in providing insights into nebular and accretionary processes.
View in article
Virtually all TIMS measurements of strontium isotopes employ a fixed 88Sr/86Sr ratio (8.375209) to correct for instrumental mass fractionation (IMF) during analysis (Papanastassiou and Wasserburg, 1969, 1978; Moynier et al., 2010; Charlier et al., 2012; Hans et al., 2013).
View in article
In comparison, MC-ICP-MS techniques using either Zr-normalisation and/or sample-standard bracketing (Moynier et al., 2010; Charlier et al., 2012) can yield 88Sr/86Sr and 87Sr/86Sr ratios to examine mass-dependent fractionation effects, but cannot accurately measure 84Sr/86Sr due to 84Kr interference.
View in article
Terrestrial samples (Fig. 1a) form a linear array that lies within error of the calculated equilibrium mass-dependent fractionation line (MDFL) produced by high temperature mass fractionation (Young et al., 2002), and cluster around the bulk silicate Earth value for δ88/86Sr of ~+0.29 ‰ (Moynier et al., 2010; Charlier et al., 2012).
View in article
Dauphas, N., Schauble, E.A. (2016) Mass fractionation laws, mass-independent effects, and isotopic anomalies. Annual Review of Earth and Planetary Sciences 44, 709–783.
 Show in context
Show in context Isotopic anomalies in extraterrestrial materials hold the keys to disentangling the origins and development of the early solar system (Dauphas and Schauble, 2016; Qin and Carlson, 2016, for recent overviews).
View in article
Moreover, the elevated apparent ∆84Sr values in two ungrouped achondrite samples (Fig. 1b; Supplementary Information, Table S-1) reflect the bulk composition since these differentiated stones are unlikely to contain any surviving pre-solar material (Dauphas and Schauble, 2016).
View in article
Halliday, A.N., Porcelli, D. (2001) In search of lost planets – the paleocosmochemistry of the inner solar system. Earth and Planetary Science Letters 192, 545–559.
 Show in context
Show in context Second, contrasting interpretations (e.g., Papanastassiou and Wasserburg, 1969; Halliday and Porcelli, 2001; Hans et al., 2013) of the disparities in initial 87Sr/86Sr ratios in BABI, Angra dos Reis and Allende should be reconsidered.
View in article
Hans, U., Kleine, T., Bourdon, B. (2013) Rb–Sr chronology of volatile depletion in differentiated protoplanets: BABI, ADOR and ALL revisited. Earth and Planetary Science Letters 374, 204–214.
 Show in context
Show in context Virtually all TIMS measurements of strontium isotopes employ a fixed 88Sr/86Sr ratio (8.375209) to correct for instrumental mass fractionation (IMF) during analysis (Papanastassiou and Wasserburg, 1969, 1978; Moynier et al., 2010; Charlier et al., 2012; Hans et al., 2013).
View in article
Second, contrasting interpretations (e.g., Papanastassiou and Wasserburg, 1969; Halliday and Porcelli, 2001; Hans et al., 2013) of the disparities in initial 87Sr/86Sr ratios in BABI, Angra dos Reis and Allende should be reconsidered.
View in article
Huss, G.R., Meshik, A.P., Smith, J.B., Hohenberg, C.M. (2003) Presolar diamond, silicon carbide, and graphite in carbonaceous chondrites: implications for thermal processing in the solar nebula. Geochimica et Cosmochimica Acta 67, 4823–4848.
 Show in context
Show in context CV3 chondrites contain less SiC than CM chondrites (Huss et al., 2003), yet we record a similar range in elevated apparent ∆84Sr values.
View in article
Kruijer, T.S., Burkhardt, C., Budde, G., Kleine, T. (2017) Age of Jupiter inferred from the distinct genetics and formation times of meteorites. Proceedings of the National Academy of Science, USA 114, 6712–6716.
 Show in context
Show in context Our data are consistent with previous proposals for a primary division between the materials represented by almost entirely undifferentiated, carbonaceous meteorites from the outer solar system, versus (almost invariably) differentiated, non-carbonaceous materials from the inner solar system (Warren, 2011; Kruijer et al., 2017).
View in article
Kruijer et al. (2017) in their proposal for a distinct contrast between inner and outer solar system domains for early-formed objects point out that differentiation sufficient to start the processes of metal separation and core formation occurred also in the outer domain.
View in article
Moynier, F., Agrainer, A., Hezel, D.C., Bouvier, A. (2010) Sr stable isotope composition of Earth, the Moon, Mars, Vesta and meteorites. Earth and Planetary Science Letters 300, 359–366.
 Show in context
Show in context Furthermore, variations caused by high temperature mass-dependent fractionation (Young et al., 2002) are also important (Patchett, 1980a,b; Moynier et al., 2010; Charlier et al., 2012) in providing insights into nebular and accretionary processes.
View in article
Virtually all TIMS measurements of strontium isotopes employ a fixed 88Sr/86Sr ratio (8.375209) to correct for instrumental mass fractionation (IMF) during analysis (Papanastassiou and Wasserburg, 1969, 1978; Moynier et al., 2010; Charlier et al., 2012; Hans et al., 2013).
View in article
In comparison, MC-ICP-MS techniques using either Zr-normalisation and/or sample-standard bracketing (Moynier et al., 2010; Charlier et al., 2012) can yield 88Sr/86Sr and 87Sr/86Sr ratios to examine mass-dependent fractionation effects, but cannot accurately measure 84Sr/86Sr due to 84Kr interference.
View in article
Terrestrial samples (Fig. 1a) form a linear array that lies within error of the calculated equilibrium mass-dependent fractionation line (MDFL) produced by high temperature mass fractionation (Young et al., 2002), and cluster around the bulk silicate Earth value for δ88/86Sr of ~+0.29 ‰ (Moynier et al., 2010; Charlier et al., 2012).
View in article
Moynier, F., Day, J.M.D., Okui, W., Yokoyama, T., Bouvier, A., Walker, R.J., Podosek, F.A. (2012) Planetary-scale strontium isotopic heterogeneity and the age of volatile depletion of early solar system materials. Astrophysical Journal 758, 45.
 Show in context
Show in contextThe weighted mean ∆84Sr of our terrestrial samples (assuming that any variation is in 84Sr alone) is -0.0002 ± 0.0083 ‰ 2 s.d. (MSWD = 4.3, n = 51), and that of the terrestrial, lunar, eucrite, diogenite and angrite feldspar samples combined is -0.0018 ± 0.0060 ‰ 2 s.d. (MSWD = 4.1, n = 78), demonstrating that the NBS-987 84Sr/86Sr composition is not at all anomalous (c.f. Moynier et al., 2012).
View in article
Additionally, differences in 84Sr/86Sr proposed between Earth, Moon and enstatite chondrites versus eucrites and ordinary chondrites (Moynier et al., 2012) are not seen in our results.
View in article
The elevated apparent ∆84Sr values we obtain from bulk samples in CI, CV and CM chondrites (Fig. 2) cannot reflect incomplete dissolution of refractory pre-solar SiC grains, with their highly depleted 84Sr (Nicolussi et al., 1998; Podosek et al., 2004; Paton et al., 2013), as such grains are not present in concentrations that would significantly affect the bulk meteorite composition (Moynier et al., 2012; Paton et al., 2013).
View in article
As an inescapable consequence of the number of isotopes available, there are two contrasting (but not mutually exclusive) possibilities for the origins of the non-mass-dependent behaviour in Sr: anomalies in p-process 84Sr (e.g., Moynier et al., 2012) and/or in r-(plus s-)process 88Sr (e.g., Qin and Carlson, 2016).
View in article
Neymark, L.A., Premo, W.R., Mel’nikov, N.N., Emsbo, P. (2014) Precise determination of δ88Sr in rocks minerals and waters by double-spike TIMS: a powerful tool in the study of geological, hydrological and biological processes. Journal of Analytical Atomic Spectrometry 29, 65–75.
 Show in context
Show in context We undertook two determinations on each sample: an unspiked measurement that is IMF-corrected and a spiked measurement which, in combination with the unspiked analysis, permits us to deconvolve the absolute ratios of 84Sr/86Sr, 88Sr/86Sr and 87Sr/86Sr, independent of any fixed IMF correction (Neymark et al., 2014).
View in article
If the radiogenic contribution to 87Sr can be accurately determined, then three-isotope plots of (87Sr/86Sr)i versus δ84/86Sr and δ88/86Sr should show in their deviations from a single MDFL which of the isotopes is anomalous, since the 87Sr/86Sr ratio generated by double-spike techniques will also reflect mass-dependent fractionation processes (Neymark et al., 2014).
View in article
Nicolussi, G.K., Pellin, M.J., Lewis, R.S., Davis, A.M., Clayton, R.N., Amari, S. (1998) Strontium isotopic composition in individual circumstellar silicon carbide grains: a record of s-process nucleosynthesis. Physical Review Letters 81, 3583–3586.
 Show in context
Show in context The elevated apparent ∆84Sr values we obtain from bulk samples in CI, CV and CM chondrites (Fig. 2) cannot reflect incomplete dissolution of refractory pre-solar SiC grains, with their highly depleted 84Sr (Nicolussi et al., 1998; Podosek et al., 2004; Paton et al., 2013), as such grains are not present in concentrations that would significantly affect the bulk meteorite composition (Moynier et al., 2012; Paton et al., 2013).
View in article
Papanastassiou, D.A., Wasserburg, G.J. (1969) Initial strontium isotopic abundances and the resolution of small time differences in the formation of planetary bodies. Earth and Planetary Science Letters 5, 361–376.
 Show in context
Show in context Virtually all TIMS measurements of strontium isotopes employ a fixed 88Sr/86Sr ratio (8.375209) to correct for instrumental mass fractionation (IMF) during analysis (Papanastassiou and Wasserburg, 1969, 1978; Moynier et al., 2010; Charlier et al., 2012; Hans et al., 2013).
View in article
Second, contrasting interpretations (e.g., Papanastassiou and Wasserburg, 1969; Halliday and Porcelli, 2001; Hans et al., 2013) of the disparities in initial 87Sr/86Sr ratios in BABI, Angra dos Reis and Allende should be reconsidered.
View in article
Papanastassiou, D.A., Wasserburg, G.J. (1978) Strontium isotopic anomalies in the Allende meteorite. Geophysical Research Letters 5, 595–598.
 Show in context
Show in context Virtually all TIMS measurements of strontium isotopes employ a fixed 88Sr/86Sr ratio (8.375209) to correct for instrumental mass fractionation (IMF) during analysis (Papanastassiou and Wasserburg, 1969, 1978; Moynier et al., 2010; Charlier et al., 2012; Hans et al., 2013).
View in article
Patchett, P.J. (1980a) Sr isotopic fractionation in Ca–Al inclusions from the Allende meteorite. Nature 283, 438–441.
 Show in context
Show in context Furthermore, variations caused by high temperature mass-dependent fractionation (Young et al., 2002) are also important (Patchett, 1980a,b; Moynier et al., 2010; Charlier et al., 2012) in providing insights into nebular and accretionary processes.
View in article
Patchett, P.J. (1980b) Sr isotopic fractionation in Allende chondrules: a reflection of solar nebular processes. Earth and Planetary Science Letters 50, 181–188.
 Show in context
Show in context Furthermore, variations caused by high temperature mass-dependent fractionation (Young et al., 2002) are also important (Patchett, 1980a,b; Moynier et al., 2010; Charlier et al., 2012) in providing insights into nebular and accretionary processes.
View in article
Paton, C., Schiller, M., Bizzarro, M. (2013) Identification of an 84Sr-depleted carrier in primitive meteorites and implications for thermal processing in the solar protoplanetary disk. Astrophysical Journal Letters 763, L40.
 Show in context
Show in context The elevated apparent ∆84Sr values we obtain from bulk samples in CI, CV and CM chondrites (Fig. 2) cannot reflect incomplete dissolution of refractory pre-solar SiC grains, with their highly depleted 84Sr (Nicolussi et al., 1998; Podosek et al., 2004; Paton et al., 2013), as such grains are not present in concentrations that would significantly affect the bulk meteorite composition (Moynier et al., 2012; Paton et al., 2013).
View in article
Podosek, F., Prombo, C., Amari, S., Lewis, R. (2004) s-process Sr isotopic compositions in presolar SiC from the Murchison meteorite. Astrophysical Journal 605, 960–965.
 Show in context
Show in context The elevated apparent ∆84Sr values we obtain from bulk samples in CI, CV and CM chondrites (Fig. 2) cannot reflect incomplete dissolution of refractory pre-solar SiC grains, with their highly depleted 84Sr (Nicolussi et al., 1998; Podosek et al., 2004; Paton et al., 2013), as such grains are not present in concentrations that would significantly affect the bulk meteorite composition (Moynier et al., 2012; Paton et al., 2013).
View in article
Qin, L., Carlson, R.W. (2016) Nucleosynthetic isotope anomalies and their cosmochemical significance. Geochemical Journal 50, 43–65.
 Show in context
Show in context Isotopic anomalies in extraterrestrial materials hold the keys to disentangling the origins and development of the early solar system (Dauphas and Schauble, 2016; Qin and Carlson, 2016, for recent overviews).
View in article
As an inescapable consequence of the number of isotopes available, there are two contrasting (but not mutually exclusive) possibilities for the origins of the non-mass-dependent behaviour in Sr: anomalies in p-process 84Sr (e.g., Moynier et al., 2012) and/or in r-(plus s-)process 88Sr (e.g., Qin and Carlson, 2016).
View in article
Rudge, J.F., Reynolds, B.C., Bourdon, B. (2009) The double spike toolbox. Chemical Geology 265, 420–431.
 Show in context
Show in contextHere we present TIMS data obtained using a double-spike methodology (Rudge et al., 2009) that, in contrast, recovers the abundance of the four Sr isotopes, free from any normalisation assumption (see Supplementary Information).
View in article
Simon, J.I., DePaolo, D.J. (2010) Stable calcium isotopic composition of meteorites and rocky planets. Earth and Planetary Science Letters 289, 457–466.
 Show in context
Show in context First, our data indicate that high temperature processes have produced resolvable mass-dependent fractionation in materials that have gone to form many of the meteorite classes (both differentiated and undifferentiated) as well as within the terrestrial and lunar materials (c.f. Simon and DePaolo, 2010).
View in article
Trinquier A., Elliott, T., Ulfbeck, D., Coath, C., Krot, A.N., Bizzarro, M. (2009) Origin of nucleosynthetic isotope heterogeneity in the solar protoplanetary disc. Science 324, 374–376.
 Show in context
Show in context This division is shown, for example, in Cr and Ti (e.g., Trinquier et al., 2009) and Mo and W (e.g., Burkhardt et al., 2012) and in our data is represented by our dual, effectively parallel MDFLs (Fig. 1a,b).
View in article
Warren, P.H. (2011) Stable-isotopic anomalies and the accretionary assemblage of the Earth and mars: a subordinate role for carbonaceous chondrites. Earth and Planetary Science Letters 311, 93–100.
 Show in context
Show in context NWA 011 similarly plots within the ‘carbonaceous chondrite’ field in Cr-Ti isotopic space (see Warren, 2011).
View in article
Our data are consistent with previous proposals for a primary division between the materials represented by almost entirely undifferentiated, carbonaceous meteorites from the outer solar system, versus (almost invariably) differentiated, non-carbonaceous materials from the inner solar system (Warren, 2011; Kruijer et al., 2017).
View in article
Note, however, that some differentiated meteorites isotopically group with the other undifferentiated samples (Tables S-1 and S-2, Figure S-1), such as NWA011 (Warren, 2011) and NWA 5400 (Burkhardt et al., 2017).
View in article
Watkins, J.M., DePaolo, D.J., Watson, E.B. (2017) Kinetic fractionation of non-traditional stable isotopes by diffusion and crystal growth reactions. Reviews in Mineralogy and Geochemistry 82, 85–125.
 Show in context
Show in context Equilibrium or kinetic fractionation effects (e.g., Blanchard et al., 2017; Watkins et al., 2017) in the data presented here can be related to two different realms of processes.
View in article
Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
 Show in context
Show in context Furthermore, variations caused by high temperature mass-dependent fractionation (Young et al., 2002) are also important (Patchett, 1980a,b; Moynier et al., 2010; Charlier et al., 2012) in providing insights into nebular and accretionary processes.
View in article
Terrestrial samples (Fig. 1a) form a linear array that lies within error of the calculated equilibrium mass-dependent fractionation line (MDFL) produced by high temperature mass fractionation (Young et al., 2002), and cluster around the bulk silicate Earth value for δ88/86Sr of ~+0.29 ‰ (Moynier et al., 2010; Charlier et al., 2012).
View in article
Linear regression on our data from all terrestrial, lunar, eucrite, diogenite, and angrite samples yields a line with a slope of -0.981 ± 0.047 (Mean Square of Weighted Deviation; MSWD = 4.1) that is identical within error to the theoretical equilibrium MDFL (slope = -0.978: Young et al., 2002).
View in article
Figure 1 [...] MDFL denotes the equilibrium mass-dependent fractionation line which passes through the origin (the assumed composition of NBS-987) with a slope of -0.978 (Young et al., 2002).
View in article
top
Supplementary Information
Sample Preparation, Dissolution and Chemical Separation
All bulk meteorite samples, with the exception of the Smithsonian Museum Allende Reference Sample, were crushed from interior chips by hand in a new agate mortar in a class 100 clean air environment at the Open University facilities. Analytical techniques used in this study follow those established by Charlier et al. (2006) with an emphasis on minimising possible terrestrial contamination and optimal chemical separation techniques. Feldspar separates from the NWA angrites, and the ungrouped achondrite bulk powders, were leached in warm ~2 M HCl for 20 minutes, rinsed in 18 Ωm MilliQ water and then dried in an oven. The leaching process was carried out in order to remove the possibility of terrestrial contamination for these ‘find’ samples. All other bulk powders were prepared from ‘falls’ and were not leached. Measured sample sizes ranged from 4.64 mg for lunar sample NWA 032 to 333.1 mg for the enstatite chondrite Abee. Samples were dissolved in a 3:1 mixture of concentrated HF–HNO3 at 130 °C on a hotplate (all reagents used were twice sub-boiling distilled in Teflon). Samples were then almost dried down before addition of aqua regia, then completely dried down before addition of 6M HCl.
Terrestrial samples were aliquots from bulk powders used for other analytical projects. All were milled in an agate Tema mill. All samples were dissolved as for the non-terrestrial samples, detailed above.
A ca. 10 % portion of the bulk dissolution was aliquotted for Rb and Sr concentration determination by isotope dilution (these data will be presented elsewhere). The remaining ~90 % of the bulk dissolution was then converted to nitrate form and finally equilibrated in 8 M HNO3. This aliquot was then further divided into two equal portions, one of which was optimally spiked with our 84Sr-87Sr double-spike (DS), the other left unspiked. The DS and natural aliquots were then dealt with completely independently, where all further manipulations and separations were carried out in separate laminar flow cabinets and only using beakers and columns specifically designated for use with spiked and natural samples, respectively. However, the number and type of manipulations for each of the spiked and unspiked aliquots were kept identical in order to remove the possibility of differential blank issues. We also chose to spike our samples prior to column separation in order to circumvent the possible problem of column-induced fractionation. Sr was separated from both aliquots using identical protocols involving sorbing the Sr onto the resin and eluting matrix elements in 8 M HNO3, followed by recovery of Sr in 0.05 M HNO3. For the SiO2-rich terrestrial samples an initial Sr pre-concentration step using Biorad columns containing 2 ml AG50W-X8 resin in 2.5 M HCl was carried out.
Samples were processed in batches of 12, alongside a total procedural blank for each batch. Strontium blanks (determined by isotope dilution using a dilute 84Sr single spike) never exceeded 18 pg. For all the Sr samples analysed throughout this study, no blank correction was applied since the analyte amount taken for mass spectrometry was of the order of hundreds of ng (usually ca. 1 µg) for both DS and natural aliquots.
Mass Spectrometry
All mass spectrometric measurements were performed using a Thermo-Finnigan Triton TIMS (thermal ionisation mass spectrometer) instrument at the Open University. The instrument is of standard configuration having 9 Faraday collectors connected to 1011 Ω feedback resistors. TIMS analysis for stable Sr consisted of two separate Sr isotope ratio measurements; a natural and spiked run, both made on outgassed zone-refined single Re filaments. A Ta2F5 activator was used to maximise ionisation efficiency and natural and spiked measurements were made on separate magazines with a clean ion source extraction plate for each magazine.
Because of the relatively small abundances of three of the Sr isotopes; 84Sr (0.56 %), 86Sr (9.86 %), 87Sr (7.00 %), it was necessary to collect a large number of ions in order to obtain high precision Sr isotope measurements. This was met by a combination of long counting times and relatively large beam intensities such that background effects are reduced on the 84Sr, 86Sr and 87Sr. Runs were carried out using an 88Sr beam intensity of 8 to 10V for 54 cycles of 10 block ratio measurements with a 16.2 second integration time.
Identical protocols were used for both the natural and spiked runs. Measurements were carried out in static mode using six amplifiers in rotation. Baselines were measured by source deflection for 2 min after each step in the amplifier rotation, with a pre-baseline wait time of 30 seconds. Two cup configurations were used during the course of this study (88Sr on H2, and 88Sr on H1) and the amplifiers were cycled through a ‘dummy’ mass (set at mass ~88.5) in both cases during the measurement routine to allow the amplifier used for 88Sr to fully discharge before then being connected to the Faraday cup measuring the smaller 84Sr beam. Without this additional step in the rotation sequence we found that our 84Sr/86Sr data were systematically shifted to higher values. Correction for any 87Rb interference at mass 87 was carried out using the beam intensity measured on 85Rb and 87Rb/85Rb = 0.385707.
Natural runs were corrected for mass fractionation in the conventional way using 86Sr/88Sr = 0.1194. All samples were run in the course of thirteen sessions, in total spaced out over several years, with the instrument being used for other isotopic systems in between. For this reason, we report our natural and double-spike data from within the individual sessions. Analysis of 77 natural NBS 987 standards over the entire course of this study (42 months) yield a long term 87Sr/86Sr mean of 0.710241 (2 s.d. = 50 ppm), but the reproducibility of standard measurements within individual sessions (run within 7–10 day periods) varies between 6 and 24 ppm. Stable Sr isotope ratios were calculated using a routine similar to that detailed by Neymark et al. (2014) where a Newton-Raphson iteration technique implemented in MatLab was used to solve the ‘true’ isotope composition in 87Sr denominator space for each of the ratios. Uncertainties were calculated using a 500 iteration Monte-Carlo simulation.
Our Sr double spike was prepared from enriched 84Sr and 87Sr spikes supplied by Oak Ridge Laboratories, resulting in an isotopic composition of 84Sr = 41.94 %, 86Sr = 2.28 %, 87Sr = 45.53 %, 88Sr = 10.26 % which was calibrated in a similar fashion to that proposed by Neymark et al. (2014). This double-spike composition is close to the optimal value suggested in the ‘cocktail list’ given by Rudge et al. (2009) and permits deconvolution of the ‘true’ isotope composition with very low error magnification over a wide range of spike-sample ratios.
Double-spike data are presented in the standard delta notation with deviations in 88Sr/86Sr and 84Sr/86Sr in per mille (‰) relative to the NBS-987 standard:
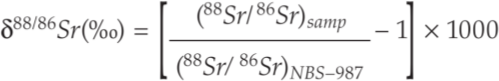
and
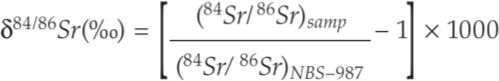
where 88Sr/86SrNBS-987 = 8.375209, and 84Sr/86SrNBS-987 = 0.056491.
An overall variability of thirteen separate analytical sessions of 0.132 ‰ in δ88/86Sr ratios, and 0.087 ‰ in δ84/86Sr ratios was observed over a period spanning 42 months. Thus, in order to account for these individual batch offsets the average of all standard measurements made in each session were normalised to δ88/86Sr and δ84/86Sr = 0, given the values above for NBS 987, and the resulting correction factor applied to all samples and standards analysed in that batch. For each batch taken individually, the external δ84/86Sr reproducibilities (2 s.d.) varied between 0.018 ‰ and 0.065 ‰, and the external δ88/86Sr reproducibilities (2 s.d.) varied between 0.0096 ‰ and 0.028 ‰.
Uncertainties and Standard Data
An aspect that is often neglected is that in the three-isotope plot such as used here the uncertainties are correlated because of a common denominator isotope, in this case 86Sr. For this study, we fully propagate the within-run Monte Carlo-derived uncertainties for individual samples, along with the external reproducibility of the deconvolved standards for that individual session. We also calculate a correlation coefficient and apply this to generate an error ellipse. This approach is needed because the shifts in isotopic composition we have measured are small, and we require fully propagated uncertainties to have confidence in our interpretations of the data, in particular the possible non-mass-dependent behaviour of 84Sr and/or 88Sr.
In conventional, internally normalised Sr isotope analysis, repeated single analyses of the NBS-987 standard are used to determine the long term external reproducibility. However, with the double-spike (DS) technique this is not as straightforward. For each batch of samples, two independent measurements are required, where measurements of the natural isotopic composition are deconvolved against DS measurements made in separate analytical sessions, as described above. With each separate magazine of natural and DS samples we measure four or five standards, respectively, with the spiked standard being a stock solution of an optimised mixture of our double spike and the NBS-987 standard. Rather than arbitrarily choosing an individual natural-standard combination for standard data deconvolution, we have deconvolved every possible permutation for the natural and spiked runs for each individual analysis period. Thus, for four or five natural, then DS standards run on consecutive magazines, we arrive at 16 or 25 possible ways, respectively, in which the double-spike deconvolution can be performed. We then determined a weighted mean and 2 s.d. uncertainty for this group of standards, which we then added quadratically to the individual uncertainties determined from the Monte Carlo-derived uncertainties for our unknowns in that particular batch. This method was chosen for two reasons. First, deconvolving data across disparate, non-sequential analytical sessions raises the possibility of biases due to small changes in cup efficiencies that arise over prolonged periods of time (since the TIMS instrument was used for other isotope systems). Second, it provides a robust and conservative estimate of the true external reproducibilities for our unknowns in a particular batch. Equivalence of data between disparate batches can then achieved by normalisation of the average standard value in a particular batch to the standard values (by definition δ88Sr and δ84Sr = 0 ‰; see below) which were used in the calibration of the double spike. In this fashion, we have both confidence in the true uncertainties and accuracy of our data, as well as equivalence of data over the course of this study.
Interpretation of Standard Data
The δ88/86Sr versus δ84/86Sr values obtained from the multiple double-spike deconvolutions of the standards have the following properties. First, the deconvolved standard values for each batch lie close to a line (intrinsic to the measurement techniques used and the instrument behaviour) in δ88/86Sr versus δ84/86Sr space. Each of the lines has a near-constant slope, across all batches and natural samples within a batch, with a combined value of -44.369º (±0.214º, 1 σ; 78 slope values). Second, the ‘along-strike’ spread of the δ88/86Sr versus δ84/86Sr values is constant within a batch.
These observations yield the following implications:
- The position of the bivariate mean of δ88/86Sr versus δ84/86Sr values depends specifically on the choice of spikes for the deconvolution.
- Because of the effectively constant slope of the MDFL over the range of δ88/86Sr versus δ84/86Sr values experienced in this work, the position of the lineation of double-spike values in the direction at right angles to the lineation is extremely well determined, within the measurement uncertainties of the double-spike values.
- Similarly, because of the effectively constant slope, the distance perpendicular to the lineation will be the same irrespective of the number of double-spike values, so it has just one degree of freedom.
Calculation of Uncertainties (Confidence Ellipses) for Standard-corrected δ88/86Sr and δ84/86Sr Data
Confidence regions for the double-spike derived strontium ratios for standards
Uncertainties in double-spike method determinations of strontium ratios are typically obtained by 500 Monte Carlo simulations assuming Gaussian statistics (Neymark et al., 2014). The correlation coefficient for δ88/86Sr/δ84/86Sr can thus be directly calculated from the 500 simulations. These correlation coefficients are very similar across all of the batches: -0.564 ± 0.072 (2 σ). The negatively signed error correlation means that confidence regions for the double-spike strontium ratios are ellipses that are slightly oblique to the MDFL.
Confidence regions for the strontium ratios of the samples
The full (Gaussian) variance matrix is calculated for each standard-corrected strontium isotopic ratio, as follows.
- A full variance matrix for the sample data point is calculated from the formal 2 σ uncertainties of the δ84/86Sr and δ88/86Sr data values, assuming the same (constant) correlation coefficient as the standards.
- Data for the standards, unknowns and their variances are rotated into the coordinate space parallel and perpendicular to the MDFL, so that the offset of the relevant (session by session) standard value in the perpendicular direction can be subtracted from that of the sample in the corresponding session. As the sample data and the standard data are independent, the variance matrices of the corrected data are the sum of the sample and standard data (in the rotated coordinate system).
- The corrected data and their variance matrices are then rotated back into standard, δ84/86Sr versus δ88/86Sr The resulting 95 % confidence regions are ellipses which are again oblique to the MDFL (Figs 1a, b and c in the main paper).
Uncertainties in the ∆84Sr and ∆88Sr values are calculated by Monte Carlo (MC) simulation using the full variance matrix for the data uncertainties, using the equations:
∆84Sr (MC) = δ84/86Sr (MC) – 1/tan θ δ88/86Sr (MC)
or
∆88Sr (MC) = δ88/86Sr (MC) – 1/tan θ δ84/86Sr (MC)
where θ is the slope of the terrestrial MDFL.
Supplementary Tables and Figures
Table S-1 Sample information and summary of Sr stable isotopic results for all samples used in this study, along with weighted means for each group of data. Details of correction for inter-batch bias, calculation of correlation coefficient and full propagation of uncertainties is given in the Supplementary Information.
| Sample | Sample type | Sample weight (mg) | Batch no. | δ84/86Sr | 2 s.d. | δ88/86Sr | 2 s.d. | correlation coefficient | Δ84Sr | 2 s.d. | MSWD | n |
| BHVO-1 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.298 | 0.028 | 0.295 | 0.014 | 0.059 | 0.003 | 0.032 | ||
| BHVO-2 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.305 | 0.024 | 0.305 | 0.013 | 0.163 | 0.006 | 0.029 | ||
| BHVO-3 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.312 | 0.025 | 0.311 | 0.013 | 0.125 | 0.005 | 0.030 | ||
| BHVO-4 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.353 | 0.022 | 0.315 | 0.013 | 0.222 | -0.031 | 0.028 | ||
| BCR-2 | Terrestrial basalt | 7.98 | 9 | -0.328 | 0.026 | 0.308 | 0.013 | 0.132 | -0.012 | 0.030 | ||
| BIR-2 | Terrestrial basalt | 19.92 | 9 | -0.297 | 0.033 | 0.298 | 0.013 | 0.063 | 0.008 | 0.037 | ||
| B | Terrestrial gabbro | 16.55 | 9 | -0.286 | 0.024 | 0.320 | 0.013 | 0.211 | 0.041 | 0.029 | ||
| C | Terrestrial gabbro | 14.32 | 9 | -0.216 | 0.033 | 0.221 | 0.013 | 0.047 | 0.010 | 0.036 | ||
| D | Terrestrial gabbro | 13.68 | 9 | -0.346 | 0.024 | 0.298 | 0.014 | 0.102 | -0.042 | 0.029 | ||
| E | Terrestrial gabbro | 15.43 | 9 | -0.344 | 0.025 | 0.329 | 0.013 | 0.180 | -0.007 | 0.031 | ||
| F | Terrestrial gabbro | 24.03 | 9 | -0.344 | 0.025 | 0.339 | 0.013 | 0.128 | 0.003 | 0.031 | ||
| G | Terrestrial gabbro | 14.36 | 9 | -0.275 | 0.023 | 0.298 | 0.013 | 0.252 | 0.029 | 0.027 | ||
| H | Terrestrial gabbro | 15.73 | 9 | -0.204 | 0.029 | 0.203 | 0.013 | 0.090 | 0.003 | 0.033 | ||
| EW93 | Terrestrial basalt | 16.41 | 9 | -0.384 | 0.027 | 0.336 | 0.013 | 0.115 | -0.041 | 0.032 | ||
| MD37 | Terrestrial basalt | 19.55 | 9 | -0.256 | 0.026 | 0.252 | 0.013 | 0.166 | 0.002 | 0.031 | ||
| YR289 | Terrestrial rhyolite | 38.45 | 11 | -0.320 | 0.027 | 0.329 | 0.013 | -0.010 | 0.017 | 0.030 | ||
| YR291 | Terrestrial rhyolite | 95.28 | 11 | -0.303 | 0.027 | 0.298 | 0.013 | 0.017 | 0.001 | 0.031 | ||
| YR292 | Terrestrial rhyolite | 38.08 | 11 | -0.298 | 0.027 | 0.326 | 0.013 | 0.007 | 0.035 | 0.029 | ||
| YR294 | Terrestrial rhyolite | 22.75 | 11 | -0.280 | 0.028 | 0.297 | 0.013 | -0.005 | 0.024 | 0.030 | ||
| YR296 | Terrestrial rhyolite | 50.2 | 11 | -0.302 | 0.026 | 0.300 | 0.013 | 0.037 | 0.005 | 0.030 | ||
| YR297 | Terrestrial rhyolite | 60.11 | 11 | -0.306 | 0.024 | 0.314 | 0.013 | 0.051 | 0.015 | 0.029 | ||
| YR300 | Terrestrial rhyolite | 35.78 | 11 | -0.297 | 0.027 | 0.290 | 0.013 | -0.013 | 0.000 | 0.029 | ||
| YR302 | Terrestrial rhyolite | 50.55 | 11 | -0.319 | 0.027 | 0.314 | 0.013 | 0.001 | 0.003 | 0.031 | ||
| YR303 | Terrestrial rhyolite | 41.61 | 11 | -0.282 | 0.036 | 0.321 | 0.013 | -0.098 | 0.047 | 0.037 | ||
| YR304 | Terrestrial rhyolite | 21.92 | 11 | -0.332 | 0.035 | 0.322 | 0.014 | -0.104 | -0.003 | 0.036 | ||
| YR305 | Terrestrial rhyolite | 26.21 | 11 | -0.306 | 0.026 | 0.314 | 0.014 | -0.010 | 0.015 | 0.029 | ||
| YR307 | Terrestrial rhyolite | 90.02 | 11 | -0.264 | 0.025 | 0.282 | 0.013 | 0.063 | 0.025 | 0.028 | ||
| YP126 | Terrestrial rhyolite | 13.8 | 1 | -0.356 | 0.021 | 0.314 | 0.007 | -0.341 | -0.035 | 0.019 | ||
| YP127 | Terrestrial rhyolite | 36.46 | 1 | -0.207 | 0.046 | 0.187 | 0.012 | -0.500 | -0.016 | 0.041 | ||
| YP045 | Terrestrial rhyolite | 35.74 | 1 | -0.186 | 0.024 | 0.187 | 0.008 | -0.381 | 0.005 | 0.022 | ||
| YP049 | Terrestrial rhyolite | 37.56 | 1 | -0.140 | 0.046 | 0.158 | 0.014 | -0.512 | 0.022 | 0.041 | ||
| YP053 | Terrestrial rhyolite | 25.56 | 1 | -0.214 | 0.035 | 0.182 | 0.013 | -0.493 | -0.027 | 0.031 | ||
| YP059 | Terrestrial rhyolite | 21.55 | 1 | -0.274 | 0.024 | 0.273 | 0.007 | -0.368 | 0.005 | 0.022 | ||
| YP060 | Terrestrial rhyolite | 27.85 | 1 | -0.278 | 0.023 | 0.274 | 0.008 | -0.380 | 0.003 | 0.021 | ||
| YP061 | Terrestrial rhyolite | 25.77 | 1 | -0.323 | 0.025 | 0.349 | 0.007 | -0.353 | 0.035 | 0.023 | ||
| YP067 | Terrestrial rhyolite | 25.82 | 1 | -0.290 | 0.060 | 0.311 | 0.019 | -0.536 | 0.028 | 0.052 | ||
| YP074 | Terrestrial rhyolite | 15.21 | 1 | -0.473 | 0.054 | 0.446 | 0.016 | -0.526 | -0.017 | 0.048 | ||
| YP079 | Terrestrial rhyolite | 38.41 | 1 | -0.315 | 0.024 | 0.305 | 0.008 | -0.398 | -0.003 | 0.022 | ||
| YP081 | Terrestrial rhyolite | 45 | 1 | -0.097 | 0.024 | 0.135 | 0.007 | -0.331 | 0.041 | 0.023 | ||
| YP083FPG | Terrestrial rhyolite | 40.23 | 4 | -0.159 | 0.025 | 0.097 | 0.010 | -0.440 | -0.060 | 0.022 | ||
| YP084 | Terrestrial rhyolite | 16.29 | 1 | -0.431 | 0.050 | 0.358 | 0.019 | -0.533 | -0.065 | 0.043 | ||
| YP131 | Terrestrial rhyolite | 51.57 | 1 | -0.255 | 0.021 | 0.215 | 0.008 | -0.367 | -0.035 | 0.019 | ||
| YP132 | Terrestrial rhyolite | 29.12 | 1 | -0.177 | 0.043 | 0.205 | 0.014 | -0.507 | 0.033 | 0.037 | ||
| YP137 | Terrestrial rhyolite | 23.8 | 1 | -0.319 | 0.054 | 0.281 | 0.018 | -0.532 | -0.031 | 0.047 | ||
| YP134 | Terrestrial rhyolite | 29.05 | 1 | -0.182 | 0.037 | 0.196 | 0.009 | -0.453 | 0.018 | 0.034 | ||
| YP136 | Terrestrial rhyolite | 54.76 | 1 | -0.076 | 0.024 | 0.134 | 0.010 | -0.433 | 0.061 | 0.022 | ||
| YP142 | Terrestrial rhyolite | 21.5 | 1 | -0.289 | 0.026 | 0.264 | 0.008 | -0.402 | -0.019 | 0.024 | ||
| YP143 | Terrestrial rhyolite | 36.96 | 1 | -0.281 | 0.023 | 0.253 | 0.007 | -0.353 | -0.022 | 0.021 | ||
| YP083SCORIA | Terrestrial basalt | 6.24 | 1 | -0.303 | 0.034 | 0.246 | 0.012 | -0.484 | -0.051 | 0.030 | ||
| YP079SC1 | Terrestrial basalt | 12.3 | 3 | -0.329 | 0.043 | 0.281 | 0.036 | -0.554 | -0.041 | 0.037 | ||
| YP079SC2 | Terrestrial basalt | 20.38 | 3 | -0.292 | 0.033 | 0.317 | 0.025 | -0.543 | 0.032 | 0.029 | ||
| Wtd mean terrestrial | 0.000 | 0.008 | 4.3 | 51 | ||||||||
| NWA 032 | Lunar | 4.64 | 12 | -0.404 | 0.026 | 0.407 | 0.015 | -0.002 | 0.013 | 0.030 | ||
| 15555 | Lunar | 27.91 | 12 | -0.336 | 0.027 | 0.324 | 0.013 | 0.084 | -0.005 | 0.031 | ||
| 67955 | Lunar | 17.92 | 12 | -0.373 | 0.024 | 0.329 | 0.014 | 0.106 | -0.036 | 0.031 | ||
| Wtd mean lunar | -0.009 | 0.063 | 2.8 | 3 | ||||||||
| Talampaya | Eucrite | 40.14 | 2 | -0.332 | 0.021 | 0.339 | 0.010 | -0.030 | 0.015 | 0.024 | ||
| Sioux County | Eucrite | 41.47 | 2 | -0.294 | 0.019 | 0.316 | 0.010 | -0.034 | 0.030 | 0.021 | ||
| Milliebillillie | Eucrite | 28.79 | 2 | -0.279 | 0.021 | 0.281 | 0.011 | -0.088 | 0.009 | 0.022 | ||
| Serra de Mage | Eucrite | 12.24 | 2 | -0.368 | 0.022 | 0.329 | 0.010 | -0.043 | -0.031 | 0.023 | ||
| Juvinas | Eucrite | 27.01 | 2 | -0.320 | 0.022 | 0.312 | 0.009 | -0.014 | 0.000 | 0.023 | ||
| Jonzac | Eucrite | 38.43 | 2 | -0.365 | 0.021 | 0.309 | 0.010 | -0.043 | -0.049 | 0.023 | ||
| Ibitera | Eucrite | 24.14 | 2 | -0.304 | 0.019 | 0.305 | 0.010 | -0.002 | 0.008 | 0.022 | ||
| Camel Donga | Eucrite | 29.63 | 2 | -0.352 | 0.018 | 0.338 | 0.009 | 0.045 | -0.006 | 0.021 | ||
| Agoult | Eucrite | 37.59 | 3 | -0.260 | 0.024 | 0.272 | 0.008 | -0.435 | 0.018 | 0.021 | ||
| Bereba | Eucrite | 33.34 | 3 | -0.371 | 0.023 | 0.363 | 0.007 | -0.413 | 0.001 | 0.021 | ||
| Emmaville | Eucrite | 33.56 | 3 | -0.412 | 0.023 | 0.371 | 0.007 | -0.408 | -0.032 | 0.021 | ||
| Lakangaon | Eucrite | 36.99 | 3 | -0.324 | 0.023 | 0.316 | 0.012 | -0.495 | 0.000 | 0.021 | ||
| Moore County | Eucrite | 32.4 | 3 | -0.451 | 0.022 | 0.438 | 0.007 | -0.408 | -0.002 | 0.021 | ||
| Stannern | Eucrite | 35.21 | 6 | -0.273 | 0.024 | 0.231 | 0.008 | -0.431 | -0.036 | 0.022 | ||
| Pasamonte | Eucrite | 34.19 | 6 | -0.305 | 0.024 | 0.296 | 0.012 | -0.494 | -0.002 | 0.021 | ||
| Johnstown | Diogenite | 153.5 | 10 | -0.330 | 0.041 | 0.273 | 0.015 | -0.138 | -0.050 | 0.041 | ||
| Shalka | Diogenite | 231.71 | 10 | -0.388 | 0.114 | 0.356 | 0.023 | -0.438 | -0.024 | 0.107 | ||
| Wtd mean HEDs | -0.006 | 0.011 | 3.8 | 17 | ||||||||
| 99555 fsp | Angrite | 7.89 | 5 | -0.321 | 0.023 | 0.342 | 0.007 | -0.361 | 0.028 | 0.021 | ||
| D'Orbigny Fsp1 | Angrite | 4.91 | 5 | -0.270 | 0.024 | 0.298 | 0.008 | -0.372 | 0.035 | 0.021 | ||
| D'Orbigny Fsp2 | Angrite | 12.94 | 5 | -0.364 | 0.027 | 0.337 | 0.008 | -0.399 | -0.019 | 0.024 | ||
| NWA 4590 fsp1 | Angrite | 16.92 | 5 | 0.300 | 0.024 | -0.285 | 0.009 | -0.413 | 0.008 | 0.022 | ||
| NWA 4590 fsp2 | Angrite | 18.26 | 5 | 0.352 | 0.032 | -0.360 | 0.010 | -0.459 | -0.016 | 0.028 | ||
| NWA 4801 fsp1 | Angrite | 23.77 | 5 | -0.080 | 0.025 | 0.071 | 0.008 | -0.396 | -0.008 | 0.023 | ||
| NWA 4801 fsp2 | Angrite | 19.34 | 5 | -0.164 | 0.024 | 0.128 | 0.008 | -0.388 | -0.032 | 0.022 | ||
| Wtd mean angrite feldspars | 0.002 | 0.024 | 5.1 | 7 | ||||||||
| Wtd mean 'differentiated' | -0.002 | 0.006 | 4.1 | 78 | ||||||||
| NWA5400 | Ungrouped achondrite | 17.86 | 12 | 0.210 | 0.035 | -0.090 | 0.020 | -0.254 | 0.119 | 0.036 | ||
| NWA011 | Ungrouped achondrite | 36.82 | 12 | -0.182 | 0.031 | 0.242 | 0.017 | -0.165 | 0.065 | 0.032 | ||
| Limerick | Ordinary chondrite H5 | 210.4 | 10 | -0.230 | 0.034 | 0.300 | 0.014 | -0.050 | 0.077 | 0.037 | ||
| Alfianello | Ordinary chondrite L6 | 205.34 | 10 | -0.241 | 0.029 | 0.265 | 0.013 | 0.089 | 0.030 | 0.033 | ||
| Harleton | Ordinary chondrite L6 | 189.76 | 10 | -0.275 | 0.025 | 0.302 | 0.013 | 0.136 | 0.035 | 0.029 | ||
| Appley Bridge | Ordinary chondrite LL6 | 207.35 | 10 | -0.264 | 0.029 | 0.243 | 0.017 | -0.108 | -0.015 | 0.032 | ||
| Dhurmsala | Ordinary chondrite LL6 | 152.55 | 10 | -0.343 | 0.028 | 0.310 | 0.014 | 0.062 | -0.026 | 0.032 | ||
| Salles | Ordinary chondrite L5 | 205.58 | 10 | -0.331 | 0.026 | 0.297 | 0.013 | 0.140 | -0.027 | 0.031 | ||
| Wtd mean ordinary chondrites | 0.009 | 0.042 | 6.1 | 6 | ||||||||
| Abee | Enstatite chondrite | 333.1 | 8 | -0.450 | 0.027 | 0.434 | 0.013 | 0.009 | -0.006 | 0.030 | ||
| Kainsaz | CO3.2 | 180.34 | 6 | -0.291 | 0.024 | 0.335 | 0.009 | -0.460 | 0.051 | 0.021 | ||
| Felix | CO3.3 | 112.16 | 8 | -0.209 | 0.024 | 0.289 | 0.014 | 0.035 | 0.086 | 0.029 | ||
| Ornans | CO3.4 | 103.89 | 6 | -0.318 | 0.025 | 0.320 | 0.007 | -0.429 | 0.010 | 0.022 | ||
| Moss | CO3.6 | 131.05 | 8 | -0.274 | 0.030 | 0.311 | 0.014 | -0.057 | 0.044 | 0.032 | ||
| Wtd mean CO chondrites | 0.044 | 0.049 | 6.3 | 4 | ||||||||
| Karoonda | CK4 | 177.77 | 6 | -0.161 | 0.023 | 0.166 | 0.008 | -0.440 | 0.009 | 0.021 | ||
| Alais | CI | 108.01 | 8 | -0.185 | 0.035 | 0.276 | 0.016 | -0.207 | 0.097 | 0.036 | ||
| Orgeuil | CI | 13.78 | 6 | -0.149 | 0.024 | 0.241 | 0.008 | -0.430 | 0.097 | 0.022 | ||
| Wtd mean CI chondrites | 0.097 | 0.018 | - | 2 | ||||||||
| Cold Bokkeveldt | CM2 | 119.33 | 6 | -0.100 | 0.023 | 0.138 | 0.007 | -0.420 | 0.041 | 0.022 | ||
| Murchison | CM2 | 101.1 | 6 | -0.183 | 0.024 | 0.323 | 0.007 | -0.424 | 0.148 | 0.022 | ||
| Murchison rpt | CM2 | 87.42 | 8 | -0.161 | 0.044 | 0.299 | 0.015 | -0.216 | 0.145 | 0.044 | ||
| Wtd mean CM2 chondrites | 0.100 | 0.160 | 26 | 3 | ||||||||
| Allende (OU) | CV3 | 152.18 | 6 | -0.049 | 0.023 | 0.116 | 0.008 | -0.432 | 0.069 | 0.021 | ||
| ALL bulk 1 (Smithsonian) | CV3 | 128.37 | 7 | 0.055 | 0.030 | 0.074 | 0.008 | -0.498 | 0.131 | 0.026 | ||
| ALL bulk 2 (Smithsonian) | CV3 | 115.28 | 7 | 0.067 | 0.029 | 0.062 | 0.006 | -0.467 | 0.131 | 0.027 | ||
| Viagarano bulk | CV3 | 203.2 | 7 | -0.010 | 0.031 | 0.139 | 0.017 | -0.542 | 0.132 | 0.026 | ||
| Efremovka | CV3 | 100.33 | 10 | -0.143 | 0.023 | 0.219 | 0.013 | 0.216 | 0.081 | 0.028 | ||
| Wtd mean CV3 chondrites | 0.106 | 0.040 | 6.6 | 5 | ||||||||
| n total | 112 |
Table S-2 Sr isotopic compositions for the samples used for regression of the ‘offset’ MDFL in Figure 1b.
| Batch no. | δ84/86Sr | 2 s.d. | δ88/86Sr | 2 s.d. | correlation coefficient | ||
| NWA5400 | Ach ung | 12 | 0.2105 | 0.0348 | -0.0896 | 0.0196 | -0.2543 |
| NWA011 | Ach ung | 12 | -0.1817 | 0.0310 | 0.2415 | 0.0172 | -0.1648 |
| Limerick | H5 chondrite | 10 | -0.2296 | 0.0337 | 0.2997 | 0.0144 | -0.0505 |
| Felix | CO3.3 | 8 | -0.2092 | 0.0243 | 0.2885 | 0.0136 | 0.0350 |
| Alais | CI1 | 8 | -0.1852 | 0.0354 | 0.2756 | 0.0163 | -0.2067 |
| Orgeuil | CI1 | 6 | -0.1494 | 0.0244 | 0.2405 | 0.0075 | -0.4301 |
| Cold Bokkeveldt | CM2 | 6 | -0.0997 | 0.0227 | 0.1379 | 0.0074 | -0.4198 |
| Murchison | CM2 | 6 | -0.1834 | 0.0238 | 0.3235 | 0.0074 | -0.4238 |
| Murchison rpt | CM2 | 8 | -0.1610 | 0.0438 | 0.2990 | 0.0152 | -0.2158 |
| Allende | CV3 | 6 | -0.0495 | 0.0232 | 0.1157 | 0.0077 | -0.4316 |
| ALL bulk 1 | CV3 | 7 | 0.0554 | 0.0297 | 0.0737 | 0.0082 | -0.4978 |
| ALL bulk 2 | CV3 | 7 | 0.0671 | 0.0293 | 0.0622 | 0.0065 | -0.4675 |
| Viagarano bulk | CV3 | 7 | -0.0100 | 0.0308 | 0.1392 | 0.0175 | -0.5422 |
| Efremovka | CV3 | 10 | -0.1429 | 0.0230 | 0.2192 | 0.0130 | 0.2156 |

Figure S-1 Plot of δ88/86Sr vs. δ84/86Sr showing the data and best fit line and error envelope for the ‘offset’ MDFL shown in Figure 1b.
Supplementary Information References
Neymark, L.A., Premo, W.R., Mel’nikov, N.N., Emsbo, P. (2014) Precise determination of δ88Sr in rocks minerals and waters by double-spike TIMS: a powerful tool in the study of geological, hydrological and biological processes. Journal of Analytical Atomic Spectrometry 29, 65–75.
Rudge, J.F., Reynolds, B.C., Bourdon, B. (2009) The double spike toolbox. Chemical Geology 265, 420–431.
Figures and Tables

Figure 1 Three-isotope plots of all terrestrial and non-terrestrial data. (a) Plot of δ88/86Sr vs δ84/86Sr showing the data for terrestrial, lunar, eucrite, diogenite and angrite samples in this study (Supplementary Information, Table S-1). MDFL denotes the equilibrium mass-dependent fractionation line which passes through the origin (the assumed composition of NBS-987) with a slope of -0.978 (Young et al., 2002
Young, E.D., Galy, A., Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
). The shaded region is the 2 s.d. error envelope around the line of best fit to the data points plotted; the line itself is analytically and visually indistinguishable from the equilibrium MDFL. Data points are represented by their 2 s.d. uncertainty envelopes calculated using the methods outlined in the Supplementary Information. (b) Plot of δ88/86Sr vs δ84/86Sr showing the data measured in this study. Data points plotted in panel a are greyed out to minimise overlap. We show two lines: a ‘terrestrial’ MDFL which is the line of best-fit to the data points shown in panel a, and an ‘offset’ MDFL calculated from ungrouped achondrites and chondrite classes CI, CV3 and CM2, together with the heavy end members of the CO and ordinary chondrite classes (see Table S-2 in Supplementary Information).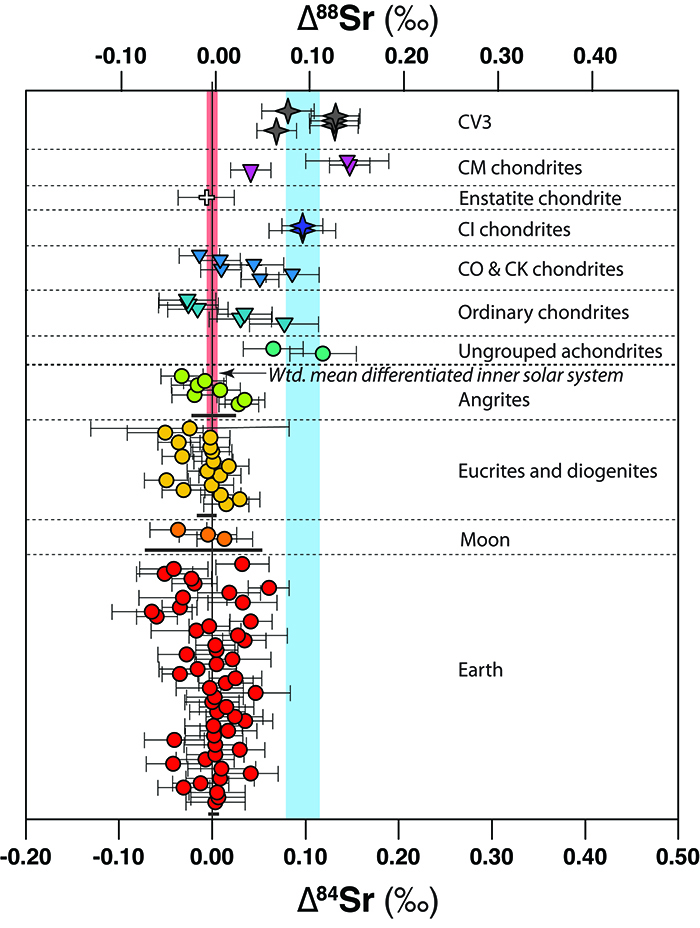
Figure 2 Plot of Δ84Sr and Δ88Sr for all samples (see Supplementary Information Table S-1 for data values). Uncertainties are 2 s.d., fully propagated (see Supplementary Information). Weighted mean values (±2 s.d.) for terrestrial, lunar, eucrite, diogenite and angrite samples are shown as horizontal grey bars for each of these data sets. The vertical pink bar extending through the ungrouped achondrite, ordinary chondrite and carbonaceous chondrite data is a weighted mean value (-0.0018 ± 0.0060, MSWD = 4.1) for the inner solar system derived from the terrestrial, lunar, eucrite, diogenite and angrite samples, and corresponds to the ‘terrestrial’ MDFL in Figure 1. The blue vertical line represents the weighted mean (±2 s.d) for the (largely undifferentiated) samples used to define the ‘offset’ MDFL (see text for details).
Back to article
Supplementary Figures and Tables
Table S-1 Sample information and summary of Sr stable isotopic results for all samples used in this study, along with weighted means for each group of data. Details of correction for inter-batch bias, calculation of correlation coefficient and full propagation of uncertainties is given in the Supplementary Information.
| Sample | Sample type | Sample weight (mg) | Batch no. | δ84/86Sr | 2 s.d. | δ88/86Sr | 2 s.d. | correlation coefficient | Δ84Sr | 2 s.d. | MSWD | n |
| BHVO-1 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.298 | 0.028 | 0.295 | 0.014 | 0.059 | 0.003 | 0.032 | ||
| BHVO-2 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.305 | 0.024 | 0.305 | 0.013 | 0.163 | 0.006 | 0.029 | ||
| BHVO-3 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.312 | 0.025 | 0.311 | 0.013 | 0.125 | 0.005 | 0.030 | ||
| BHVO-4 | Terrestrial basalt | 1/4 of 35.53 | 9 | -0.353 | 0.022 | 0.315 | 0.013 | 0.222 | -0.031 | 0.028 | ||
| BCR-2 | Terrestrial basalt | 7.98 | 9 | -0.328 | 0.026 | 0.308 | 0.013 | 0.132 | -0.012 | 0.030 | ||
| BIR-2 | Terrestrial basalt | 19.92 | 9 | -0.297 | 0.033 | 0.298 | 0.013 | 0.063 | 0.008 | 0.037 | ||
| B | Terrestrial gabbro | 16.55 | 9 | -0.286 | 0.024 | 0.320 | 0.013 | 0.211 | 0.041 | 0.029 | ||
| C | Terrestrial gabbro | 14.32 | 9 | -0.216 | 0.033 | 0.221 | 0.013 | 0.047 | 0.010 | 0.036 | ||
| D | Terrestrial gabbro | 13.68 | 9 | -0.346 | 0.024 | 0.298 | 0.014 | 0.102 | -0.042 | 0.029 | ||
| E | Terrestrial gabbro | 15.43 | 9 | -0.344 | 0.025 | 0.329 | 0.013 | 0.180 | -0.007 | 0.031 | ||
| F | Terrestrial gabbro | 24.03 | 9 | -0.344 | 0.025 | 0.339 | 0.013 | 0.128 | 0.003 | 0.031 | ||
| G | Terrestrial gabbro | 14.36 | 9 | -0.275 | 0.023 | 0.298 | 0.013 | 0.252 | 0.029 | 0.027 | ||
| H | Terrestrial gabbro | 15.73 | 9 | -0.204 | 0.029 | 0.203 | 0.013 | 0.090 | 0.003 | 0.033 | ||
| EW93 | Terrestrial basalt | 16.41 | 9 | -0.384 | 0.027 | 0.336 | 0.013 | 0.115 | -0.041 | 0.032 | ||
| MD37 | Terrestrial basalt | 19.55 | 9 | -0.256 | 0.026 | 0.252 | 0.013 | 0.166 | 0.002 | 0.031 | ||
| YR289 | Terrestrial rhyolite | 38.45 | 11 | -0.320 | 0.027 | 0.329 | 0.013 | -0.010 | 0.017 | 0.030 | ||
| YR291 | Terrestrial rhyolite | 95.28 | 11 | -0.303 | 0.027 | 0.298 | 0.013 | 0.017 | 0.001 | 0.031 | ||
| YR292 | Terrestrial rhyolite | 38.08 | 11 | -0.298 | 0.027 | 0.326 | 0.013 | 0.007 | 0.035 | 0.029 | ||
| YR294 | Terrestrial rhyolite | 22.75 | 11 | -0.280 | 0.028 | 0.297 | 0.013 | -0.005 | 0.024 | 0.030 | ||
| YR296 | Terrestrial rhyolite | 50.2 | 11 | -0.302 | 0.026 | 0.300 | 0.013 | 0.037 | 0.005 | 0.030 | ||
| YR297 | Terrestrial rhyolite | 60.11 | 11 | -0.306 | 0.024 | 0.314 | 0.013 | 0.051 | 0.015 | 0.029 | ||
| YR300 | Terrestrial rhyolite | 35.78 | 11 | -0.297 | 0.027 | 0.290 | 0.013 | -0.013 | 0.000 | 0.029 | ||
| YR302 | Terrestrial rhyolite | 50.55 | 11 | -0.319 | 0.027 | 0.314 | 0.013 | 0.001 | 0.003 | 0.031 | ||
| YR303 | Terrestrial rhyolite | 41.61 | 11 | -0.282 | 0.036 | 0.321 | 0.013 | -0.098 | 0.047 | 0.037 | ||
| YR304 | Terrestrial rhyolite | 21.92 | 11 | -0.332 | 0.035 | 0.322 | 0.014 | -0.104 | -0.003 | 0.036 | ||
| YR305 | Terrestrial rhyolite | 26.21 | 11 | -0.306 | 0.026 | 0.314 | 0.014 | -0.010 | 0.015 | 0.029 | ||
| YR307 | Terrestrial rhyolite | 90.02 | 11 | -0.264 | 0.025 | 0.282 | 0.013 | 0.063 | 0.025 | 0.028 | ||
| YP126 | Terrestrial rhyolite | 13.8 | 1 | -0.356 | 0.021 | 0.314 | 0.007 | -0.341 | -0.035 | 0.019 | ||
| YP127 | Terrestrial rhyolite | 36.46 | 1 | -0.207 | 0.046 | 0.187 | 0.012 | -0.500 | -0.016 | 0.041 | ||
| YP045 | Terrestrial rhyolite | 35.74 | 1 | -0.186 | 0.024 | 0.187 | 0.008 | -0.381 | 0.005 | 0.022 | ||
| YP049 | Terrestrial rhyolite | 37.56 | 1 | -0.140 | 0.046 | 0.158 | 0.014 | -0.512 | 0.022 | 0.041 | ||
| YP053 | Terrestrial rhyolite | 25.56 | 1 | -0.214 | 0.035 | 0.182 | 0.013 | -0.493 | -0.027 | 0.031 | ||
| YP059 | Terrestrial rhyolite | 21.55 | 1 | -0.274 | 0.024 | 0.273 | 0.007 | -0.368 | 0.005 | 0.022 | ||
| YP060 | Terrestrial rhyolite | 27.85 | 1 | -0.278 | 0.023 | 0.274 | 0.008 | -0.380 | 0.003 | 0.021 | ||
| YP061 | Terrestrial rhyolite | 25.77 | 1 | -0.323 | 0.025 | 0.349 | 0.007 | -0.353 | 0.035 | 0.023 | ||
| YP067 | Terrestrial rhyolite | 25.82 | 1 | -0.290 | 0.060 | 0.311 | 0.019 | -0.536 | 0.028 | 0.052 | ||
| YP074 | Terrestrial rhyolite | 15.21 | 1 | -0.473 | 0.054 | 0.446 | 0.016 | -0.526 | -0.017 | 0.048 | ||
| YP079 | Terrestrial rhyolite | 38.41 | 1 | -0.315 | 0.024 | 0.305 | 0.008 | -0.398 | -0.003 | 0.022 | ||
| YP081 | Terrestrial rhyolite | 45 | 1 | -0.097 | 0.024 | 0.135 | 0.007 | -0.331 | 0.041 | 0.023 | ||
| YP083FPG | Terrestrial rhyolite | 40.23 | 4 | -0.159 | 0.025 | 0.097 | 0.010 | -0.440 | -0.060 | 0.022 | ||
| YP084 | Terrestrial rhyolite | 16.29 | 1 | -0.431 | 0.050 | 0.358 | 0.019 | -0.533 | -0.065 | 0.043 | ||
| YP131 | Terrestrial rhyolite | 51.57 | 1 | -0.255 | 0.021 | 0.215 | 0.008 | -0.367 | -0.035 | 0.019 | ||
| YP132 | Terrestrial rhyolite | 29.12 | 1 | -0.177 | 0.043 | 0.205 | 0.014 | -0.507 | 0.033 | 0.037 | ||
| YP137 | Terrestrial rhyolite | 23.8 | 1 | -0.319 | 0.054 | 0.281 | 0.018 | -0.532 | -0.031 | 0.047 | ||
| YP134 | Terrestrial rhyolite | 29.05 | 1 | -0.182 | 0.037 | 0.196 | 0.009 | -0.453 | 0.018 | 0.034 | ||
| YP136 | Terrestrial rhyolite | 54.76 | 1 | -0.076 | 0.024 | 0.134 | 0.010 | -0.433 | 0.061 | 0.022 | ||
| YP142 | Terrestrial rhyolite | 21.5 | 1 | -0.289 | 0.026 | 0.264 | 0.008 | -0.402 | -0.019 | 0.024 | ||
| YP143 | Terrestrial rhyolite | 36.96 | 1 | -0.281 | 0.023 | 0.253 | 0.007 | -0.353 | -0.022 | 0.021 | ||
| YP083SCORIA | Terrestrial basalt | 6.24 | 1 | -0.303 | 0.034 | 0.246 | 0.012 | -0.484 | -0.051 | 0.030 | ||
| YP079SC1 | Terrestrial basalt | 12.3 | 3 | -0.329 | 0.043 | 0.281 | 0.036 | -0.554 | -0.041 | 0.037 | ||
| YP079SC2 | Terrestrial basalt | 20.38 | 3 | -0.292 | 0.033 | 0.317 | 0.025 | -0.543 | 0.032 | 0.029 | ||
| Wtd mean terrestrial | 0.000 | 0.008 | 4.3 | 51 | ||||||||
| NWA 032 | Lunar | 4.64 | 12 | -0.404 | 0.026 | 0.407 | 0.015 | -0.002 | 0.013 | 0.030 | ||
| 15555 | Lunar | 27.91 | 12 | -0.336 | 0.027 | 0.324 | 0.013 | 0.084 | -0.005 | 0.031 | ||
| 67955 | Lunar | 17.92 | 12 | -0.373 | 0.024 | 0.329 | 0.014 | 0.106 | -0.036 | 0.031 | ||
| Wtd mean lunar | -0.009 | 0.063 | 2.8 | 3 | ||||||||
| Talampaya | Eucrite | 40.14 | 2 | -0.332 | 0.021 | 0.339 | 0.010 | -0.030 | 0.015 | 0.024 | ||
| Sioux County | Eucrite | 41.47 | 2 | -0.294 | 0.019 | 0.316 | 0.010 | -0.034 | 0.030 | 0.021 | ||
| Milliebillillie | Eucrite | 28.79 | 2 | -0.279 | 0.021 | 0.281 | 0.011 | -0.088 | 0.009 | 0.022 | ||
| Serra de Mage | Eucrite | 12.24 | 2 | -0.368 | 0.022 | 0.329 | 0.010 | -0.043 | -0.031 | 0.023 | ||
| Juvinas | Eucrite | 27.01 | 2 | -0.320 | 0.022 | 0.312 | 0.009 | -0.014 | 0.000 | 0.023 | ||
| Jonzac | Eucrite | 38.43 | 2 | -0.365 | 0.021 | 0.309 | 0.010 | -0.043 | -0.049 | 0.023 | ||
| Ibitera | Eucrite | 24.14 | 2 | -0.304 | 0.019 | 0.305 | 0.010 | -0.002 | 0.008 | 0.022 | ||
| Camel Donga | Eucrite | 29.63 | 2 | -0.352 | 0.018 | 0.338 | 0.009 | 0.045 | -0.006 | 0.021 | ||
| Agoult | Eucrite | 37.59 | 3 | -0.260 | 0.024 | 0.272 | 0.008 | -0.435 | 0.018 | 0.021 | ||
| Bereba | Eucrite | 33.34 | 3 | -0.371 | 0.023 | 0.363 | 0.007 | -0.413 | 0.001 | 0.021 | ||
| Emmaville | Eucrite | 33.56 | 3 | -0.412 | 0.023 | 0.371 | 0.007 | -0.408 | -0.032 | 0.021 | ||
| Lakangaon | Eucrite | 36.99 | 3 | -0.324 | 0.023 | 0.316 | 0.012 | -0.495 | 0.000 | 0.021 | ||
| Moore County | Eucrite | 32.4 | 3 | -0.451 | 0.022 | 0.438 | 0.007 | -0.408 | -0.002 | 0.021 | ||
| Stannern | Eucrite | 35.21 | 6 | -0.273 | 0.024 | 0.231 | 0.008 | -0.431 | -0.036 | 0.022 | ||
| Pasamonte | Eucrite | 34.19 | 6 | -0.305 | 0.024 | 0.296 | 0.012 | -0.494 | -0.002 | 0.021 | ||
| Johnstown | Diogenite | 153.5 | 10 | -0.330 | 0.041 | 0.273 | 0.015 | -0.138 | -0.050 | 0.041 | ||
| Shalka | Diogenite | 231.71 | 10 | -0.388 | 0.114 | 0.356 | 0.023 | -0.438 | -0.024 | 0.107 | ||
| Wtd mean HEDs | -0.006 | 0.011 | 3.8 | 17 | ||||||||
| 99555 fsp | Angrite | 7.89 | 5 | -0.321 | 0.023 | 0.342 | 0.007 | -0.361 | 0.028 | 0.021 | ||
| D'Orbigny Fsp1 | Angrite | 4.91 | 5 | -0.270 | 0.024 | 0.298 | 0.008 | -0.372 | 0.035 | 0.021 | ||
| D'Orbigny Fsp2 | Angrite | 12.94 | 5 | -0.364 | 0.027 | 0.337 | 0.008 | -0.399 | -0.019 | 0.024 | ||
| NWA 4590 fsp1 | Angrite | 16.92 | 5 | 0.300 | 0.024 | -0.285 | 0.009 | -0.413 | 0.008 | 0.022 | ||
| NWA 4590 fsp2 | Angrite | 18.26 | 5 | 0.352 | 0.032 | -0.360 | 0.010 | -0.459 | -0.016 | 0.028 | ||
| NWA 4801 fsp1 | Angrite | 23.77 | 5 | -0.080 | 0.025 | 0.071 | 0.008 | -0.396 | -0.008 | 0.023 | ||
| NWA 4801 fsp2 | Angrite | 19.34 | 5 | -0.164 | 0.024 | 0.128 | 0.008 | -0.388 | -0.032 | 0.022 | ||
| Wtd mean angrite feldspars | 0.002 | 0.024 | 5.1 | 7 | ||||||||
| Wtd mean 'differentiated' | -0.002 | 0.006 | 4.1 | 78 | ||||||||
| NWA5400 | Ungrouped achondrite | 17.86 | 12 | 0.210 | 0.035 | -0.090 | 0.020 | -0.254 | 0.119 | 0.036 | ||
| NWA011 | Ungrouped achondrite | 36.82 | 12 | -0.182 | 0.031 | 0.242 | 0.017 | -0.165 | 0.065 | 0.032 | ||
| Limerick | Ordinary chondrite H5 | 210.4 | 10 | -0.230 | 0.034 | 0.300 | 0.014 | -0.050 | 0.077 | 0.037 | ||
| Alfianello | Ordinary chondrite L6 | 205.34 | 10 | -0.241 | 0.029 | 0.265 | 0.013 | 0.089 | 0.030 | 0.033 | ||
| Harleton | Ordinary chondrite L6 | 189.76 | 10 | -0.275 | 0.025 | 0.302 | 0.013 | 0.136 | 0.035 | 0.029 | ||
| Appley Bridge | Ordinary chondrite LL6 | 207.35 | 10 | -0.264 | 0.029 | 0.243 | 0.017 | -0.108 | -0.015 | 0.032 | ||
| Dhurmsala | Ordinary chondrite LL6 | 152.55 | 10 | -0.343 | 0.028 | 0.310 | 0.014 | 0.062 | -0.026 | 0.032 | ||
| Salles | Ordinary chondrite L5 | 205.58 | 10 | -0.331 | 0.026 | 0.297 | 0.013 | 0.140 | -0.027 | 0.031 | ||
| Wtd mean ordinary chondrites | 0.009 | 0.042 | 6.1 | 6 | ||||||||
| Abee | Enstatite chondrite | 333.1 | 8 | -0.450 | 0.027 | 0.434 | 0.013 | 0.009 | -0.006 | 0.030 | ||
| Kainsaz | CO3.2 | 180.34 | 6 | -0.291 | 0.024 | 0.335 | 0.009 | -0.460 | 0.051 | 0.021 | ||
| Felix | CO3.3 | 112.16 | 8 | -0.209 | 0.024 | 0.289 | 0.014 | 0.035 | 0.086 | 0.029 | ||
| Ornans | CO3.4 | 103.89 | 6 | -0.318 | 0.025 | 0.320 | 0.007 | -0.429 | 0.010 | 0.022 | ||
| Moss | CO3.6 | 131.05 | 8 | -0.274 | 0.030 | 0.311 | 0.014 | -0.057 | 0.044 | 0.032 | ||
| Wtd mean CO chondrites | 0.044 | 0.049 | 6.3 | 4 | ||||||||
| Karoonda | CK4 | 177.77 | 6 | -0.161 | 0.023 | 0.166 | 0.008 | -0.440 | 0.009 | 0.021 | ||
| Alais | CI | 108.01 | 8 | -0.185 | 0.035 | 0.276 | 0.016 | -0.207 | 0.097 | 0.036 | ||
| Orgeuil | CI | 13.78 | 6 | -0.149 | 0.024 | 0.241 | 0.008 | -0.430 | 0.097 | 0.022 | ||
| Wtd mean CI chondrites | 0.097 | 0.018 | - | 2 | ||||||||
| Cold Bokkeveldt | CM2 | 119.33 | 6 | -0.100 | 0.023 | 0.138 | 0.007 | -0.420 | 0.041 | 0.022 | ||
| Murchison | CM2 | 101.1 | 6 | -0.183 | 0.024 | 0.323 | 0.007 | -0.424 | 0.148 | 0.022 | ||
| Murchison rpt | CM2 | 87.42 | 8 | -0.161 | 0.044 | 0.299 | 0.015 | -0.216 | 0.145 | 0.044 | ||
| Wtd mean CM2 chondrites | 0.100 | 0.160 | 26 | 3 | ||||||||
| Allende (OU) | CV3 | 152.18 | 6 | -0.049 | 0.023 | 0.116 | 0.008 | -0.432 | 0.069 | 0.021 | ||
| ALL bulk 1 (Smithsonian) | CV3 | 128.37 | 7 | 0.055 | 0.030 | 0.074 | 0.008 | -0.498 | 0.131 | 0.026 | ||
| ALL bulk 2 (Smithsonian) | CV3 | 115.28 | 7 | 0.067 | 0.029 | 0.062 | 0.006 | -0.467 | 0.131 | 0.027 | ||
| Viagarano bulk | CV3 | 203.2 | 7 | -0.010 | 0.031 | 0.139 | 0.017 | -0.542 | 0.132 | 0.026 | ||
| Efremovka | CV3 | 100.33 | 10 | -0.143 | 0.023 | 0.219 | 0.013 | 0.216 | 0.081 | 0.028 | ||
| Wtd mean CV3 chondrites | 0.106 | 0.040 | 6.6 | 5 | ||||||||
| n total | 112 |
Table S-2 Sr isotopic compositions for the samples used for regression of the ‘offset’ MDFL in Figure 1b.
| Batch no. | δ84/86Sr | 2 s.d. | δ88/86Sr | 2 s.d. | correlation coefficient | ||
| NWA5400 | Ach ung | 12 | 0.2105 | 0.0348 | -0.0896 | 0.0196 | -0.2543 |
| NWA011 | Ach ung | 12 | -0.1817 | 0.0310 | 0.2415 | 0.0172 | -0.1648 |
| Limerick | H5 chondrite | 10 | -0.2296 | 0.0337 | 0.2997 | 0.0144 | -0.0505 |
| Felix | CO3.3 | 8 | -0.2092 | 0.0243 | 0.2885 | 0.0136 | 0.0350 |
| Alais | CI1 | 8 | -0.1852 | 0.0354 | 0.2756 | 0.0163 | -0.2067 |
| Orgeuil | CI1 | 6 | -0.1494 | 0.0244 | 0.2405 | 0.0075 | -0.4301 |
| Cold Bokkeveldt | CM2 | 6 | -0.0997 | 0.0227 | 0.1379 | 0.0074 | -0.4198 |
| Murchison | CM2 | 6 | -0.1834 | 0.0238 | 0.3235 | 0.0074 | -0.4238 |
| Murchison rpt | CM2 | 8 | -0.1610 | 0.0438 | 0.2990 | 0.0152 | -0.2158 |
| Allende | CV3 | 6 | -0.0495 | 0.0232 | 0.1157 | 0.0077 | -0.4316 |
| ALL bulk 1 | CV3 | 7 | 0.0554 | 0.0297 | 0.0737 | 0.0082 | -0.4978 |
| ALL bulk 2 | CV3 | 7 | 0.0671 | 0.0293 | 0.0622 | 0.0065 | -0.4675 |
| Viagarano bulk | CV3 | 7 | -0.0100 | 0.0308 | 0.1392 | 0.0175 | -0.5422 |
| Efremovka | CV3 | 10 | -0.1429 | 0.0230 | 0.2192 | 0.0130 | 0.2156 |
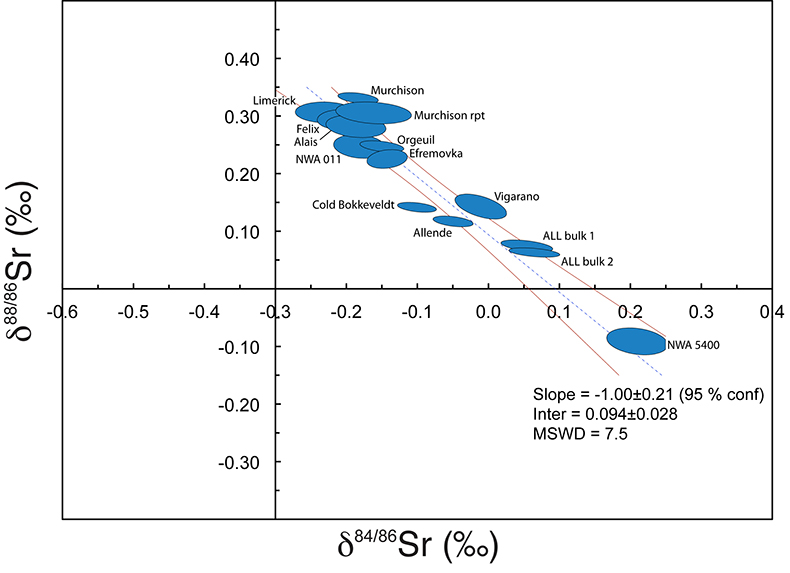
Figure S-1 Plot of δ88/86Sr vs. δ84/86Sr showing the data and best fit line and error envelope for the ‘offset’ MDFL shown in Figure 1b.