The solubility of heat-producing elements in Earth’s core
Affiliations | Corresponding Author | Cite as | Funding informationKeywords: core formation, heat sources, metal-silicate partitioning experiments, potassium, uranium
- Share this article
Article views:9,343Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract
Figures and Tables
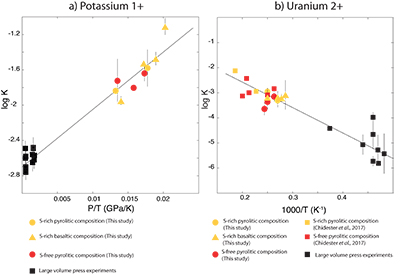 Figure 1 Thermodynamic models of K and U partitioning between metal and silicate. (a) Equilibrium constant for potassium metal-silicate partitioning (Eq. 1) as a function of P/T. The line corresponds to the least squares fit (R2 = 0.94) of the thermodynamic model (Eq. 3) with a = -2.7 ± 0.03 and c = 65 ± 2.5. (b) Equilibrium constant of uranium metal-silicate partitioning (Eq. 2) as a function of the reciprocal temperature. The line corresponds to the least squares fit (R2 = 0.91) of the thermodynamic model (Eq. 4) with a = -0.55 ± 0.21, b = -10133 ± 642 and εUO = -31. |  Table 1 Coefficients from Eqs. 4, 5 (and S-3, S-4) obtained by least squares linear regression of the experimental data, along with their associated (1 sigma) uncertainties. Details of the calculation are given in the Supplementary Information. | Figure 2 Concentration of K and U in the core from continuous core-formation models, assuming two magma ocean geotherms: cool (A1,2,3) and warm (B1,2,3). The top panel is the abundance of 238U and 235U as a function of time, the middle panel corresponds to that of 40K as a function of time, and the bottom panel is the total power produced in the core by the radioactive decay of these three radionuclides over time. |
| Figure 1 | Table 1 | Figure 2 |
Supplementary Figures and Tables
| Table S-1 Composition of starting materials. The basalt and Met 1 have been measured by EPMA, whereas the pyrolite has been measured using EDX. Fe is Alfa Aesar spherical iron powder (stock number 00170). N stands for the number of analyses that have been carried. | Table S-2 Experimental conditions. Pressure has been corrected for thermal pressure following Siebert et al. (2012). Oxygen fugacity of each run has been calculated relative to the IW buffer using an ideal model assuming the activity of iron in metal and silicate is 1. The estimated uncertainties for temperatures and pressures are ±150 K and ±5 GPa respectively (e.g., Fiquet et al., 2010; Siebert et al., 2012). | Table S-3 Composition of the metallic phases. *Totals include Cu, Zn, Mn and Pb which are not reported here. N stands for the number of analyses that have been performed. | Table S-4 Composition of the metallic phase given as mol. %. N stands for the number of analyses that have been performed. | Table S-5 Compositions of silicate phases. N stands for the number of analyses that have been performed. |
| Table S-1 | Table S-2 | Table S-3 | Table S-4 | Table S-5 |
| Table S-6 Literature data that have been used along with our data to perform thermodynamic regression. | 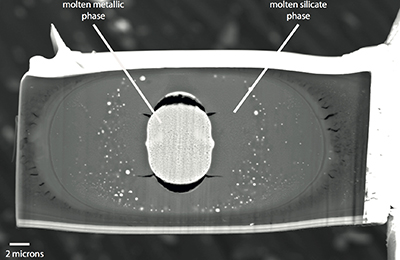 Figure S-1 Backscattered scanning electron microscopy (FEG-SEM) image of a typical recovered sample. Samples are excavated from the melted region, thinned down to a thickness of ~3 microns, and welded to a TEM grid using a FIB instrument. The metal and silicate phases are analysed by electron microprobe analysis. | 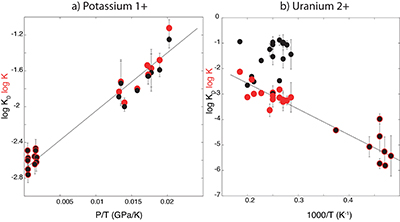 Figure S-2 Comparison of equilibrium constant (log K) and the exchange coefficient (log KD) for potassium (a) and uranium (b) metal-silicate exchange reactions. The difference between log(K) and log(KD) is the activity coefficient ratio |
| Table S-6 | Figure S-1 | Figure S-2 |
. While activities are limited for potassium (a), because all interaction parameters are 0, they are obvious in uranium (b) because of a large interaction parameter between U and O in the metal.top
Introduction
The long term thermal evolution of the core plays a fundamental role in the potential of a terrestrial planet to sustain life. Indeed, the existence of a magnetic field is one of the tenets of planetary habitability, which is generated by a geodynamo operating in the planet’s convective liquid core. The present day geodynamo is mainly driven by compositional buoyancy, due to light element release by the crystallisation of the inner core. A core with large thermal conductivity (e.g., Pozzo et al., 2012
Pozzo, M., Davies, C., Gubbins, D., Alfè, D. (2012) Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358.
; Ohta et al., 2016Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., Ohishi, Y. (2016) Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature 534, 95–98.
) yields a young age (less than 1 Gyr) for the inner core (Labrosse, 2015Labrosse, S. (2015) Thermal evolution of the core with a high thermal conductivity. Physics of the Earth and Planetary Interiors, 247, 36–55.
; Nimmo, 2015aNimmo, F. (2015a) Energetics of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 27–55.
), which is in apparent contradiction with palaeomagnetic evidence for an old geodynamo dating back to at least 3.5 Ga (Tarduno et al., 2010Tarduno, J.A., Cottrell, R.D., Watkeys, M.K., Hofmann, A., Doubrovine, P.V., Mamajek, E.E., Liu, D., Sibeck, D.G., Neukirch, L.P., Usui, Y. (2010) Geodynamo, solar wind, and magnetopause 3.4 to 3.45 billion years ago. Science 327, 1238–1240.
). Even with a low core thermal conductivity (Konôpková et al., 2016Konôpková, Z., McWilliams, R.S., Gómez-Pérez, N., Goncharov, A.F. (2016) Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 534, 99–101.
), the problem is partially mitigated, in that a dynamo can be sustained for 3.5 Gyr (e.g., Labrosse, 2003Labrosse, S. (2003) Thermal and magnetic evolution of the Earth’s core. Physics of the Earth and Planetary Interiors 140, 127–143.
; Nimmo, 2015aNimmo, F. (2015a) Energetics of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 27–55.
), but initial core temperatures are very high, above 7000 K, which implies a fully molten Earth for extended periods of time.Recently, MgO exsolution (Badro et al., 2016
Badro, J., Siebert, J., Nimmo, F. (2016) An early geodynamo driven by exsolution of mantle components from Earth’s core. Nature 536, 326–328.
) and SiO2 crystallisation (Hirose et al., 2017Hirose, K., Morard, G., Sinmyo, R., Umemoto, K., Hernlund, J., Helffrich, G., Labrosse, S. (2017) Crystallization of silicon dioxide and compositional evolution of the Earth’s core. Nature 543, 99–102.
) have been proposed as an alternative source of chemical buoyancy to drive a dynamo prior to inner core growth. These are potent sources of energy and dissipation, and while they both eradicate the need for a hot initial core, their effect is not predicted to kick in until 1 to 2 Gyr after Earth’s formation for MgO, and even later for SiO2, leaving the Earth devoid of a geodynamo, assuming a young inner core age.One possible mechanism to drive a very early dynamo, in the first billion years of Earth’s history, is the dissolution of radioactive heat-producing elements in the core during formation (Gubbins et al., 2003
Gubbins, D., Alfe, D., Masters, G., Price, G.D. Gillan, M.J. (2003) Can the Earth’s dynamo run on heat alone? Geophysical Journal International 155, 609–622.
). Because radionuclide abundance decreases with time, the process is dominant very early in Earth’s history and vanishes with time. Potassium and uranium are the main sources of heat in the Earth, and their incorporation in the core has been thoroughly examined through the years (e.g., Buffett, 2002Buffett, B.A. (2002) Estimates of heat flow in the deep mantle based on the power requirements for the geodynamo. Geophysical Research Letters 29, 7.1–7.4.
; Gubbins et al., 2003Gubbins, D., Alfe, D., Masters, G., Price, G.D. Gillan, M.J. (2003) Can the Earth’s dynamo run on heat alone? Geophysical Journal International 155, 609–622.
; Labrosse, 2003Labrosse, S. (2003) Thermal and magnetic evolution of the Earth’s core. Physics of the Earth and Planetary Interiors 140, 127–143.
, 2015Labrosse, S. (2015) Thermal evolution of the core with a high thermal conductivity. Physics of the Earth and Planetary Interiors, 247, 36–55.
; Nimmo et al., 2004Nimmo, F., Price, G.D., Brodholt, J., Gubbins, D. (2004) The influence of potassium on core and geodynamo evolution. Geophysical Journal International 156, 363–376.
), and it was shown that the incorporation of ~100s of ppm K in the core would mitigate the young inner core/early geodynamo/hot initial core conundrum.Both K and U are nominally lithophile elements, with no predisposition to fractionate in the metallic phase during metal-silicate equilibration. Bukowinski (1976)
Bukowinski, M.S.T. (1976) The effect of pressure on the physics and chemistry of potassium. Geophysical Research Letters 3, 491–494.
proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996)Parker, L.J., Atou, T., Badding, J.V. (1996) Transition element-like chemistry for potassium under pressure. Science 273, 95–96.
, which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002Gessmann, C.K., Wood, B.J. (2002) Potassium in the Earth’s core? Earth and Planetary Science Letters 200, 63–78.
; Murthy et al., 2003Murthy, V.R., Van Westrenen, W., Fei, Y. (2003) Experimental evidence that potassium is a substantial radioactive heat source in planetary cores. Nature 423, 163–165.
; Bouhifd et al., 2007Bouhifd, M.A., Gautron, L., Bolfan-Casanova, N., Malavergne, V., Hammouda, T., Andrault, D., Jephcoat, A.P. (2007) Potassium partitioning into molten iron alloys at high-pressure: Implications for Earth's core. Physics of the Earth and Planetary Interiors 160, 22–33.
; Corgne et al., 2007Corgne, A., Keshav, S., Fei, Y., McDonough, W.F. (2007) How much potassium is in the Earth's core? New insights from partitioning experiments? Earth and Planetary Science Letters 256, 567–576.
).Similarly, uranium partitioning studies (LVP) have shown a limited solubility in the metal, recently confirmed by a study of U partitioning in the laser-heated diamond anvil cell (LH-DAC). U was shown to become more siderophile with: (i) increasing sulphur content in the metal (Wheeler et al., 2006
Wheeler, K.T., Walker, D., Fei, Y., Minarik, W.G., McDonough, W.F. (2006) Experimental partitioning of uranium between liquid iron sulfide and liquid silicate: Implications for radioactivity in the Earth’s core. Geochimica et Cosmochimica Acta 70, 1537–1547.
; Malavergne et al., 2007Malavergne, V., Tarrida, M., Combes, R., Bureau, H., Jones, J., Schwandt, C. (2007) New high-pressure and high-temperature metal/silicate partitioning of U and Pb: Implications for the cores of the Earth and Mars. Geochimica et Cosmochimica Acta 71, 2637–2655.
; Bouhifd et al., 2013Bouhifd, M.A., Andrault, D., Bolfan-Casanova, N., Hammouda, T., Devidal, J.L. (2013) Metal–silicate partitioning of Pb and U: Effects of metal composition and oxygen fugacity. Geochimica et Cosmochimica Acta 114, 13–28.
; Chidester et al., 2017Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
), (ii) high temperatures (Chidester et al., 2017Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
), and (iii) low SiO2 concentration in the silicate (Chidester et al., 2017Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
). However, even in the most favourable conditions, including an unrealistically high sulphur content of the core (8 wt. %), no more than 3.5 ppb U could be dissolved in the core (Chidester et al., 2017Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
), providing no more than 2.4 TW as early as 4.5 Gyr ago, which is insufficient to have any effect on an early geodynamo.The solubility of thorium, the other major radioactive element in the Earth, in metal was not addressed in the present work as LH-DAC experiments from Chidester et al., 2017
Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
showed no measurable Th in the metallic phases.top
Experiments and Results
Here we investigated the metal-silicate partitioning of both U and K at the relevant P-T conditions of core formation, through LH-DAC experiments. Two silicate compositions were used (pyrolitic and basaltic) to examine the effect of silicate composition on partitioning; similarly, several metal compositions (with various amount of S, Si and O dissolved) were used to examine the effect of metal composition on that same partitioning (see Supplementary Information and Table S-1). The samples were compressed to 41 to 81 GPa and laser-heated to 3600 to 4100 K (Table S-2), achieving conditions above the liquidus of both metal and silicate and efficiently melting the sample. Thin sections were recovered from the centre of the laser-heated area using a focused ion beam (Fig. S-1) and analysed using an electron probe (Tables S-3 and S-5).
K and U partitioning between metal and silicate are driven by an exchange reaction involving Fe in the metal and FeO in the silicate, and are written as:
Eq. 2
Fe + UO ↔ U + FeO
The equilibrium constants K of reactions (1) and (2) are a function of P, T, and can be expressed as a function of the reaction’s exchange coefficient (D) and activity coefficients (γ):
Eq. 3
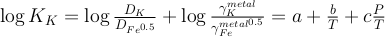
Eq. 4
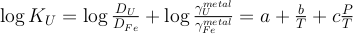
Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
) and combined our data with values from the literature (see Table S-6) to perform a least squares linear fit (details of the fitting procedure are in the Supplementary Information) for all the parameters of the equilibrium constant (Eq. 3 and Eq. 4).The data and the fitted regressions are plotted in Figure 1, and the parameters resulting from the fit are listed in Table 1. We find that potassium has no measurable interaction with O, Si, or S in the metal. Its partitioning in the metal shows a strong pressure dependence (c = 65 ± 2.5 K/GPa) but no intrinsic temperature dependence (b = 0 K), as can be seen from the excellent linear fit to the data (R2 = 0.94). Uranium, on the other hand, has a very strong interaction parameter with oxygen in the metal, as illustrated from our fitted value of εUO = -31, which signals that oxygen dissolved in the metal enhances the siderophile behaviour of uranium. No measurable effect of Si and S on U partitioning was found. Lastly, a strong temperature dependence (b = -10133 ± 642 K) and no pressure dependence (c = 0 K/GPa) were found, as can be seen once again by the excellent linear fit (R2 = 0.91). A detailed discussion and comparison of these results with previous estimates is provided in Supplementary Information.
Figure 1 Thermodynamic models of K and U partitioning between metal and silicate. (a) Equilibrium constant for potassium metal-silicate partitioning (Eq. 1) as a function of P/T. The line corresponds to the least squares fit (R2 = 0.94) of the thermodynamic model (Eq. 3) with a = -2.7 ± 0.03 and c = 65 ± 2.5. (b) Equilibrium constant of uranium metal-silicate partitioning (Eq. 2) as a function of the reciprocal temperature. The line corresponds to the least squares fit (R2 = 0.91) of the thermodynamic model (Eq. 4) with a = -0.55 ± 0.21, b = -10133 ± 642 and εUO = -31.
Table 1 Coefficients from Eqs. 3, 4 (and S-3, S-4) obtained by least squares linear regression of the experimental data, along with their associated (1 sigma) uncertainties. Details of the calculation are given in the Supplementary Information.
| Element i | a | b (K) | c (K/GPa) | εOi (1873 K) | εSi (1873 K) | εSii (1873 K) |
| Potassium | –2.7 (0.03) | 0 | 65 (2.5) | 0 | 0 | 0 |
| Uranium | –0.55 (0.21) | –10133 (642) | 0 | –31 | 0 | 0 |
top
Discussion
Our results were incorporated in a continuous core formation model (Badro et al., 2015
Badro, J., Brodholt, J.P., Piet, H., Siebert, J., Ryerson, F.J. (2015) Core formation and core composition from coupled geochemical and geophysical constraints. Proceedings of the National Academy of Sciences 112, 12310–12314.
), using two different magma ocean geotherms: cool (Andrault et al., 2011Andrault, D., Bolfan-Casanova, N., Nigro, G.L., Bouhifd, M.A., Garbarino, G., Mezouar, M. (2011) Solidus and liquidus profiles of chondritic mantle: Implication for melting of the Earth across its history. Earth and Planetary Science Letters 304, 251–259.
) and warm (Fiquet et al., 2010Fiquet, G., Auzende, A.L., Siebert, J., Corgne, A., Bureau, H., Ozawa, H., Garbarino, G. (2010) Melting of peridotite to 140 gigapascals. Science 329, 1516–1518.
) liquidus, and calculated the concentration of U and K in the core (see Supplementary Information for details). Along a cool geotherm, up to 26 ppm K (corresponding to 40 ppb 40K) can be dissolved in the core (Fig. 2), with less than 0.3 ppm U 4.5 Gyr ago. This produces at most 7.5 TW of radiogenic power after core formation, and decreases to 4 TW after 1 Gyr. Along a warm geotherm (Fig. 2), more uranium (2.5 ppb) can be dissolved in the core, owing its steep partitioning temperature dependence, along with less potassium (13 ppm K — corresponding to 20 ppb 40K) owing to its partitioning increasing with P/T, therefore decreasing in a hotter magma ocean. Since K is a significantly more efficient heat production element than U, the total power produced is surprisingly smaller in a warm than in a cool geotherm: the maximum power generated is 6 TW after core formation and decreases to 3 TW after 1 Gyr.In either case, the heat production is lower than the minimum heat flow of 15 TW proposed by Nimmo (2015b)
Nimmo, F. (2015b) Thermal and Compositional Evolution of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 201–209.
to drive a geodynamo. Similarly, Labrosse (2015)Labrosse, S. (2015) Thermal evolution of the core with a high thermal conductivity. Physics of the Earth and Planetary Interiors, 247, 36–55.
showed that the contribution of K in the total dissipation (required to drive a dynamo) is low, even with a core containing 200 ppm K (an order of magnitude higher than our estimates). Our results therefore confirm that heat-producing elements dissolved in the core cannot sustain an early geodynamo.With a core containing 26 ppm potassium, the initial temperature of the core is virtually unchanged compared to a core containing no K (Labrosse, 2015
Labrosse, S. (2015) Thermal evolution of the core with a high thermal conductivity. Physics of the Earth and Planetary Interiors, 247, 36–55.
; Nimmo, 2015bNimmo, F. (2015b) Thermal and Compositional Evolution of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 201–209.
). Therefore, core-mantle boundary temperatures lie above the silicate solidus for an extended period of time (Labrosse, 2015Labrosse, S. (2015) Thermal evolution of the core with a high thermal conductivity. Physics of the Earth and Planetary Interiors, 247, 36–55.
), supporting the existence of a basal magma ocean (Labrosse et al., 2007Labrosse, S., Hernlund, J.W., Coltice, N. (2007) A crystallizing dense magma ocean at the base of the Earth's mantle. Nature 450, 866–869.
). The influence of a limited concentration of heat-producing elements in the core on the age of the inner core is negligible. Finally, the heat flow coming from the core nowadays is estimated to be of 12 ± 5 TW (Nimmo, 2015bNimmo, F. (2015b) Thermal and Compositional Evolution of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 201–209.
). We show here that potassium and uranium together contribute at most 1 TW of the overall heat production of the core today.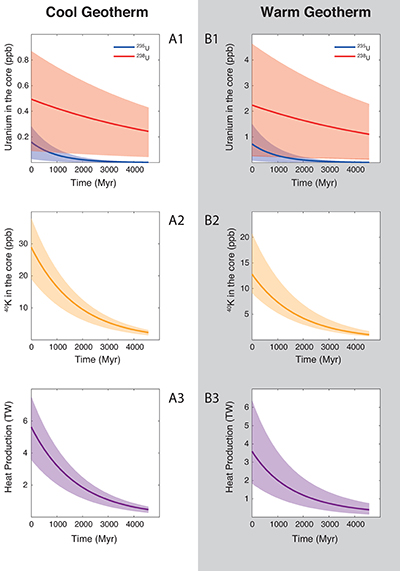
Figure 2 Concentration of K and U in the core from continuous core-formation models, assuming two magma ocean geotherms: cool (A1,2,3) and warm (B1,2,3). The top panel is the abundance of 238U and 235U as a function of time, the middle panel corresponds to that of 40K as a function of time, and the bottom panel is the total power produced in the core by the radioactive decay of these three radionuclides over time.
top
Conclusions
We measured the simultaneous metal-silicate partitioning of potassium and uranium at the putative high pressure and high temperature conditions of core formation, using laser-heated diamond anvil cell experiments. Potassium solubility in the core increases with pressure and decreases with temperature, whereas uranium solubility in the core increases with temperature and with the oxygen concentration in the core. Despite a higher solubility of those elements in liquid metal compared to low pressure-temperature experiments, the amount dissolved in the core during core formation is too low to have an effect on an early dynamo, the initial temperature of the core or the age or the inner core.
top
Acknowledgements
This manuscript benefitted from the reviews of two anonymous reviewers that are thanked for their constructive comments. We would like to thank Michel Fialin for his help with EPMA measurements, and Brandon Mahan for his aid in preparing the starting materials. We acknowledge the financial support of the UnivEarthS Labex program at Sorbonne Paris Cité (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02). This work was supported by IPGP multidisciplinary program PARI, and by Paris-IdF SESAME Grant no. 12015908. This work has been written while IB was in BGI, supported by DFG Projekt RU 1323/10-1. JB acknowledges funding from the PNP research program at INSU/CNRS, and the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement n° 207467 (DECore). JS acknowledges funding from the PNP research program at INSU/CNRS and the French National Research Agency (ANR project VolTerre, grant no. ANR-14-CE33-0017-01).
Editor: Wendy Mao
top
References
Andrault, D., Bolfan-Casanova, N., Nigro, G.L., Bouhifd, M.A., Garbarino, G., Mezouar, M. (2011) Solidus and liquidus profiles of chondritic mantle: Implication for melting of the Earth across its history. Earth and Planetary Science Letters 304, 251–259.
Show in context Our results were incorporated in a continuous core formation model (Badro et al., 2015), using two different magma ocean geotherms: cool (Andrault et al., 2011) and warm (Fiquet et al., 2010) liquidus, and calculated the concentration of U and K in the core (see Supplementary Information for details).
View in article
Badro, J., Brodholt, J.P., Piet, H., Siebert, J., Ryerson, F.J. (2015) Core formation and core composition from coupled geochemical and geophysical constraints. Proceedings of the National Academy of Sciences 112, 12310–12314.
Show in context Our results were incorporated in a continuous core formation model (Badro et al., 2015), using two different magma ocean geotherms: cool (Andrault et al., 2011) and warm (Fiquet et al., 2010) liquidus, and calculated the concentration of U and K in the core (see Supplementary Information for details).
View in article
Badro, J., Siebert, J., Nimmo, F. (2016) An early geodynamo driven by exsolution of mantle components from Earth’s core. Nature 536, 326–328.
Show in context Recently, MgO exsolution (Badro et al., 2016) and SiO2 crystallisation (Hirose et al., 2017) have been proposed as an alternative source of chemical buoyancy to drive a dynamo prior to inner core growth.
View in article
Bouhifd, M.A., Gautron, L., Bolfan-Casanova, N., Malavergne, V., Hammouda, T., Andrault, D., Jephcoat, A.P. (2007) Potassium partitioning into molten iron alloys at high-pressure: Implications for Earth's core. Physics of the Earth and Planetary Interiors 160, 22–33.
Show in context Bukowinski (1976) proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996), which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007; Corgne et al., 2007).
View in article
Bouhifd, M.A., Andrault, D., Bolfan-Casanova, N., Hammouda, T., Devidal, J.L. (2013) Metal–silicate partitioning of Pb and U: Effects of metal composition and oxygen fugacity. Geochimica et Cosmochimica Acta 114, 13–28.
Show in context U was shown to become more siderophile with: (i) increasing sulphur content in the metal (Wheeler et al., 2006; Malavergne et al., 2007; Bouhifd et al., 2013; Chidester et al., 2017), (ii) high temperatures (Chidester et al., 2017), and (iii) low SiO2 concentration in the silicate (Chidester et al., 2017).
View in article
Buffett, B.A. (2002) Estimates of heat flow in the deep mantle based on the power requirements for the geodynamo. Geophysical Research Letters 29, 7.1–7.4.
Show in context Potassium and uranium are the main sources of heat in the Earth, and their incorporation in the core has been thoroughly examined through the years (e.g., Buffett, 2002; Gubbins et al., 2003; Labrosse, 2003, 2015; Nimmo et al., 2004), and it was shown that the incorporation of ~100s of ppm K in the core would mitigate the young inner core/early geodynamo/hot initial core conundrum.
View in article
Bukowinski, M.S.T. (1976) The effect of pressure on the physics and chemistry of potassium. Geophysical Research Letters 3, 491–494.
Show in context Bukowinski (1976) proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996), which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007; Corgne et al., 2007).
View in article
Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
Show in context U was shown to become more siderophile with: (i) increasing sulphur content in the metal (Wheeler et al., 2006; Malavergne et al., 2007; Bouhifd et al., 2013; Chidester et al., 2017), (ii) high temperatures (Chidester et al., 2017), and (iii) low SiO2 concentration in the silicate (Chidester et al., 2017).
View in article
However, even in the most favourable conditions, including an unrealistically high sulphur content of the core (8 wt. %), no more than 3.5 ppb U could be dissolved in the core (Chidester et al., 2017), providing no more than 2.4 TW as early as 4.5 Gyr ago, which is insufficient to have any effect on an early geodynamo.
View in article
The solubility of thorium, the other major radioactive element in the Earth, in metal was not addressed in the present work as LH-DAC experiments from Chidester et al. (2017) showed no measurable Th in the metallic phases.
View in article
We used a valence of +1 for potassium, and +2 for uranium (as proposed by Chidester et al., 2017) and combined our data with values from the literature (see Table S-6) to perform a least squares linear fit (details of the fitting procedure are in the Supplementary Information) for all the parameters of the equilibrium constant (Eq. 3 and Eq. 4).
View in article
Corgne, A., Keshav, S., Fei, Y., McDonough, W.F. (2007) How much potassium is in the Earth's core? New insights from partitioning experiments? Earth and Planetary Science Letters 256, 567–576.
Show in context Bukowinski (1976) proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996), which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007; Corgne et al., 2007).
View in article
Fiquet, G., Auzende, A.L., Siebert, J., Corgne, A., Bureau, H., Ozawa, H., Garbarino, G. (2010) Melting of peridotite to 140 gigapascals. Science 329, 1516–1518.
Show in context Our results were incorporated in a continuous core formation model (Badro et al., 2015), using two different magma ocean geotherms: cool (Andrault et al., 2011) and warm (Fiquet et al., 2010) liquidus, and calculated the concentration of U and K in the core (see Supplementary Information for details).
View in article
Gessmann, C.K., Wood, B.J. (2002) Potassium in the Earth’s core? Earth and Planetary Science Letters 200, 63–78.
Show in context Bukowinski (1976) proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996), which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007; Corgne et al., 2007).
View in article
Gubbins, D., Alfe, D., Masters, G., Price, G.D. Gillan, M.J. (2003) Can the Earth’s dynamo run on heat alone? Geophysical Journal International 155, 609–622.
Show in context One possible mechanism to drive a very early dynamo, in the first billion years of Earth’s history, is the dissolution of radioactive heat-producing elements in the core during formation (Gubbins et al., 2003).
View in article
Potassium and uranium are the main sources of heat in the Earth, and their incorporation in the core has been thoroughly examined through the years (e.g., Buffett, 2002; Gubbins et al., 2003; Labrosse, 2003, 2015; Nimmo et al., 2004), and it was shown that the incorporation of ~100s of ppm K in the core would mitigate the young inner core/early geodynamo/hot initial core conundrum.
View in article
Hirose, K., Morard, G., Sinmyo, R., Umemoto, K., Hernlund, J., Helffrich, G., Labrosse, S. (2017) Crystallization of silicon dioxide and compositional evolution of the Earth’s core. Nature 543, 99–102.
Show in context Recently, MgO exsolution (Badro et al., 2016) and SiO2 crystallisation (Hirose et al., 2017) have been proposed as an alternative source of chemical buoyancy to drive a dynamo prior to inner core growth.
View in article
Konôpková, Z., McWilliams, R.S., Gómez-Pérez, N., Goncharov, A.F. (2016) Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 534, 99–101.
Show in context Even with a low core thermal conductivity (Konôpková et al., 2016), the problem is partially mitigated, in that a dynamo can be sustained for 3.5 Gyr (e.g., Labrosse, 2003; Nimmo, 2015a), but initial core temperatures are very high, above 7000 K, which implies a fully molten Earth for extended periods of time.
View in article
Labrosse, S. (2003) Thermal and magnetic evolution of the Earth’s core. Physics of the Earth and Planetary Interiors 140, 127–143.
Show in context Potassium and uranium are the main sources of heat in the Earth, and their incorporation in the core has been thoroughly examined through the years (e.g., Buffett, 2002; Gubbins et al., 2003; Labrosse, 2003, 2015; Nimmo et al., 2004), and it was shown that the incorporation of ~100s of ppm K in the core would mitigate the young inner core/early geodynamo/hot initial core conundrum.
View in article
Even with a low core thermal conductivity (Konôpková et al., 2016), the problem is partially mitigated, in that a dynamo can be sustained for 3.5 Gyr (e.g., Labrosse, 2003; Nimmo, 2015a), but initial core temperatures are very high, above 7000 K, which implies a fully molten Earth for extended periods of time.
View in article
Labrosse, S. (2015) Thermal evolution of the core with a high thermal conductivity. Physics of the Earth and Planetary Interiors, 247, 36–55.
Show in context A core with large thermal conductivity (e.g., Pozzo et al., 2012; Ohta et al., 2016) yields a young age (less than 1 Gyr) for the inner core (Labrosse, 2015; Nimmo, 2015a), which is in apparent contradiction with palaeomagnetic evidence for an old geodynamo dating back to at least 3.5 Ga (Tarduno et al., 2010).
View in article
Potassium and uranium are the main sources of heat in the Earth, and their incorporation in the core has been thoroughly examined through the years (e.g., Buffett, 2002; Gubbins et al., 2003; Labrosse, 2003, 2015; Nimmo et al., 2004), and it was shown that the incorporation of ~100s of ppm K in the core would mitigate the young inner core/early geodynamo/hot initial core conundrum.
View in article
Similarly, Labrosse (2015) showed that the contribution of K in the total dissipation (required to drive a dynamo) is low, even with a core containing 200 ppm K (an order of magnitude higher than our estimates).
View in article
With a core containing 26 ppm potassium, the initial temperature of the core is virtually unchanged compared to a core containing no K (Labrosse, 2015; Nimmo, 2015b).
View in article
Therefore, core-mantle boundary temperatures lie above the silicate solidus for an extended period of time (Labrosse, 2015), supporting the existence of a basal magma ocean (Labrosse et al., 2007).
View in article
Labrosse, S., Hernlund, J.W., Coltice, N. (2007) A crystallizing dense magma ocean at the base of the Earth's mantle. Nature 450, 866–869.
Show in context Therefore, core-mantle boundary temperatures lie above the silicate solidus for an extended period of time (Labrosse, 2015), supporting the existence of a basal magma ocean (Labrosse et al., 2007).
View in article
Malavergne, V., Tarrida, M., Combes, R., Bureau, H., Jones, J., Schwandt, C. (2007) New high-pressure and high-temperature metal/silicate partitioning of U and Pb: Implications for the cores of the Earth and Mars. Geochimica et Cosmochimica Acta 71, 2637–2655.
Show in context U was shown to become more siderophile with: (i) increasing sulphur content in the metal (Wheeler et al., 2006; Malavergne et al., 2007; Bouhifd et al., 2013; Chidester et al., 2017), (ii) high temperatures (Chidester et al., 2017), and (iii) low SiO2 concentration in the silicate (Chidester et al., 2017).
View in article
Murthy, V.R., Van Westrenen, W., Fei, Y. (2003) Experimental evidence that potassium is a substantial radioactive heat source in planetary cores. Nature 423, 163–165.
Show in context Bukowinski (1976) proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996), which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007; Corgne et al., 2007).
View in article
Nimmo, F. (2015a) Energetics of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 27–55.
Show in context A core with large thermal conductivity (e.g., Pozzo et al., 2012; Ohta et al., 2016) yields a young age (less than 1 Gyr) for the inner core (Labrosse, 2015; Nimmo, 2015a), which is in apparent contradiction with palaeomagnetic evidence for an old geodynamo dating back to at least 3.5 Ga (Tarduno et al., 2010).
View in article
Even with a low core thermal conductivity (Konôpková et al., 2016), the problem is partially mitigated, in that a dynamo can be sustained for 3.5 Gyr (e.g., Labrosse, 2003; Nimmo, 2015a), but initial core temperatures are very high, above 7000 K, which implies a fully molten Earth for extended periods of time.
View in article
Nimmo, F. (2015b) Thermal and Compositional Evolution of the Core. In: Schubert, G. (Ed.) Treatise on Geophysics. Second Edition. Elsevier, Amsterdam, Oxford, Burlington, 201–209.
Show in context In either case, the heat production is lower than the minimum heat flow of 15 TW proposed by Nimmo (2015b) to drive a geodynamo.
View in article
With a core containing 26 ppm potassium, the initial temperature of the core is virtually unchanged compared to a core containing no K (Labrosse, 2015; Nimmo, 2015b).
View in article
Finally, the heat flow coming from the core nowadays is estimated to be of 12 ± 5 TW (Nimmo, 2015b).
View in article
Nimmo, F., Price, G.D., Brodholt, J., Gubbins, D. (2004) The influence of potassium on core and geodynamo evolution. Geophysical Journal International 156, 363–376.
Show in context Potassium and uranium are the main sources of heat in the Earth, and their incorporation in the core has been thoroughly examined through the years (e.g., Buffett, 2002; Gubbins et al., 2003; Labrosse, 2003, 2015; Nimmo et al., 2004), and it was shown that the incorporation of ~100s of ppm K in the core would mitigate the young inner core/early geodynamo/hot initial core conundrum.
View in article
Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., Ohishi, Y. (2016) Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature 534, 95–98.
Show in context A core with large thermal conductivity (e.g., Pozzo et al., 2012; Ohta et al., 2016) yields a young age (less than 1 Gyr) for the inner core (Labrosse, 2015; Nimmo, 2015a), which is in apparent contradiction with palaeomagnetic evidence for an old geodynamo dating back to at least 3.5 Ga (Tarduno et al., 2010).
View in article
Parker, L.J., Atou, T., Badding, J.V. (1996) Transition element-like chemistry for potassium under pressure. Science 273, 95–96.
Show in context Bukowinski (1976) proposed that potassium might become a transition metal at high pressure, with the ability to dissolve easily in core-forming metal, later confirmed experimentally by Parker et al. (1996), which motivated a suite of metal-silicate experiments (performed below 25 GPa in large-volume presses - LVP) to address and quantify the partitioning of potassium between metal and silicate during Earth’s differentiation (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007; Corgne et al., 2007).
View in article
Pozzo, M., Davies, C., Gubbins, D., Alfè, D. (2012) Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358.
Show in context A core with large thermal conductivity (e.g., Pozzo et al., 2012; Ohta et al., 2016) yields a young age (less than 1 Gyr) for the inner core (Labrosse, 2015; Nimmo, 2015a), which is in apparent contradiction with palaeomagnetic evidence for an old geodynamo dating back to at least 3.5 Ga (Tarduno et al., 2010).
View in article
Tarduno, J.A., Cottrell, R.D., Watkeys, M.K., Hofmann, A., Doubrovine, P.V., Mamajek, E.E., Liu, D., Sibeck, D.G., Neukirch, L.P., Usui, Y. (2010) Geodynamo, solar wind, and magnetopause 3.4 to 3.45 billion years ago. Science 327, 1238–1240.
Show in context A core with large thermal conductivity (e.g., Pozzo et al., 2012; Ohta et al., 2016) yields a young age (less than 1 Gyr) for the inner core (Labrosse, 2015; Nimmo, 2015a), which is in apparent contradiction with palaeomagnetic evidence for an old geodynamo dating back to at least 3.5 Ga (Tarduno et al., 2010).
View in article
Wheeler, K.T., Walker, D., Fei, Y., Minarik, W.G., McDonough, W.F. (2006) Experimental partitioning of uranium between liquid iron sulfide and liquid silicate: Implications for radioactivity in the Earth’s core. Geochimica et Cosmochimica Acta 70, 1537–1547.
Show in context U was shown to become more siderophile with: (i) increasing sulphur content in the metal (Wheeler et al., 2006; Malavergne et al., 2007; Bouhifd et al., 2013; Chidester et al., 2017), (ii) high temperatures (Chidester et al., 2017), and (iii) low SiO2 concentration in the silicate (Chidester et al., 2017).
View in article
top
Supplementary Information
Methods
Starting material
Recent studies have suggested that metal and silicate composition influences potassium and uranium metal-silicate partitioning (Gessmann and Wood, 2002; Bouhifd et al., 2007, 2013; Corgne et al., 2007; Malavergne et al., 2007; Chidester et al., 2017). In order to separate those effects, we experimented with various compositions: pyrolite and basaltic starting compositions for the silicates, and metals with various amounts of sulphur, silicon and oxygen.
Our basaltic composition was obtained by grinding and mixing natural MORB with uranium and potassium oxide (decarbonated potassium carbonate). Then, we fully melted and equilibrated this basalt with a S-rich metal in a 150 ton end-loaded piston cylinder press (IPGP). This experiment was performed at 1400 °C and 1.5 GPa, and lasted 30 minutes in polycrystalline MgO capsule. This has been proved to be sufficient to approach chemical equilibrium (Thibault and Walter, 1995). We recovered both the metal and the basaltic glass to serve in our LH-DAC experiments as starting materials.
We used a synthetic composition for pyrolite. High purity oxides and carbonates were ground and mixed in an agate mortar. Subsequently, the samples were decarbonated, fused, equilibrated and quenched in an aerodynamic levitation laser furnace (IPGP) in an oxygen-rich flux (Auzende et al., 2011) to produce glass beads of 1–2 mm in diameter.
The starting materials were recovered and analysed using EPMA at Camparis, and their compositions are reported in Table S-1. The two silicates (basalt and pyrolite glasses) were then hand polished down to a double-parallel wafer about 20 microns thick, and then machined using a picosecond laser micromachining instrument (IPGP) to cut small discs of 60 and 120 microns in diameter to be loaded in the DAC. As for the S-bearing metal synthesised in the piston cylinder press, it was crushed and ground to a fine-grained powder. During high P-T equilibration with the silicate, the metal was enriched in various amounts of Si and O hence providing a suite of S–Si–O bearing metals.
Diamond anvil cell experiments
We used a diamond anvil cell equipped with culets of 200 and 300 microns in diameter. We first calibrated the Raman shift of the diamonds with pressure, in order to avoid using a ruby chip during our runs (Akahama and Kawamura, 2004). Rhenium gaskets of 250 micron thickness were indented to 40–50 microns. A hole, slightly larger than the sample disks, was laser-drilled in the centre of the indentation. A silicate disk was first placed in the sample chamber, then a small amount of metal (either S-rich or S-poor) powder was deposited in the middle of the silicate disk, and last another silicate disk of the same composition added on the top of it.
Samples were first pressurised to target pressure and then heated from both sides using infrared fibre lasers. Temperatures were continuously measured by a spectro-radiometric technique (Benedetti and Loubeyre, 2004). Temperature targets were quickly attained and maintained for 15 to 45 seconds before quenching the run by electronically switching off the laser power, providing extremely high cooling rates, and pressure was released slowly to ambient. At those extremely high temperatures, runs are fully molten, as indicated by reaching a plateau in temperature vs. laser power. Pressure was corrected for thermal pressure following ∆? = 2.7 MPa/K as proposed by Siebert et al. (2012) in accordance with estimates from Fiquet et al. (2010) and Andrault et al. (2011). Table S-2 summarises our run conditions.
Recovery of samples and analytical procedure
A focused ion beam instrument (FIB) coupled with a field emission scanning electron microscope (FE-SEM) was used (IPGP) to recover the samples. The laser-heated spot was clearly visible on secondary electron images, creating a small bump on the surface of each sample. We first deposited about one micron of platinum strip on the laser-heated area to protect the sample from further ion bombardment. Small thin sections of samples (3 microns thickness) were cut in the compressional axis using the ion beam along all sample widths. An in situ micromanipulator was used to remove the sample from the rhenium gasket and to weld it with a platinum deposit to a TEM grid. A SEM image of a recovered run is displayed in Figure S-1.
We analysed the samples using EDX spectroscopy on the FE-SEM and EPMA Cameca SX-five at IPGP (Camparis, Université Pierre et Marie Curie/IPGP). We used a beam current of 20 nA and 20 keV on both phases with a focused beam. Standards used in these analyses are diopside for Mg, Ca; orthopyroxene for Si, K and Al; Fe2O3 for iron; albite for Na, apatite for P, FeS2 for sulphur, MnTi for Ti and Mn, and UO2 for uranium. Counting time was 20–10 s on the peak and background for major elements, and 40–20 s for uranium. Composition of metallic and silicate phases are reported in Tables S-3 and S-5. Occasionally, small metallic droplets (about ~500 nm to 2 μm diameter) were trapped in the silicate upon quench, before coalescing with the main central molten iron blob. These particles were carefully avoided during analysis. Analytical transects were also performed in the silicate to assess the effect of secondary fluorescence on our measurements. We found that the silicate showed no contamination from the main metallic blob until distances below 1 µm which could be certainly resolved analytically.
Carbon contamination is difficult to address in these experiments due to the relatively high detection limit of carbon with the WDX technique (~1 wt. %). However, as with other superliquidus experiments carried out in DAC (e.g., Siebert et al., 2012, 2013), the molten region is well isolated thermally and chemically from the diamonds by a surrounding layer of unreacted MORB glass (Fig. S-1). Carbon contents of these previous experiments were measured below the detection limit (i.e. less than 1 wt. %). Additionally, we carried qualitative analyses with EDX comparing the peak intensity of C in metal (the phase that would likely incorporate carbon in case of carbon diffusion from the diamonds) and in the silicate and found similar intensities, which is an additional indication that no carbon (or a negligible amount) is present in our runs. Other DAC metal-silicate partitioning work (Fischer et al., 2015) tried to investigate the carbon contamination in metal by TEM-EELS technique and found similar low degrees of contamination. In the light of these previous works where similar experimental protocols were used, we believe that it is safe to assume that carbon contamination was limited to below 1 wt. %.
Thermodynamics
Metal-silicate partitioning of a siderophile element M of valence n can be modelled as an exchange reaction such as:
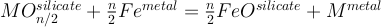
The metal-silicate partitioning coefficient of such an element (
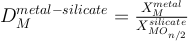, with X the molar fraction of the elementM) is a function of temperature (T), pressure (P), oxygen fugacity (fO2) and metal and silicate composition. To get rid of oxygen fugacity dependency, one can use the exchange coefficient such as
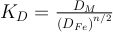.The equilibrium constant related to Eq. S-1 is directly related to so that:
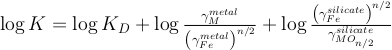
The activity coefficients (γ) in the silicate are taken constant at 1 in our runs and the ones in the metal are calculated following the work of Ma (2001). This approach allows us to describe quantitatively the thermodynamics of multicomponent metallic solutions for both dilute and concentrated levels, using interaction parameters. The activity coefficient of iron and the N-1 solutes i in a metallic solution containing N components are expressed as:
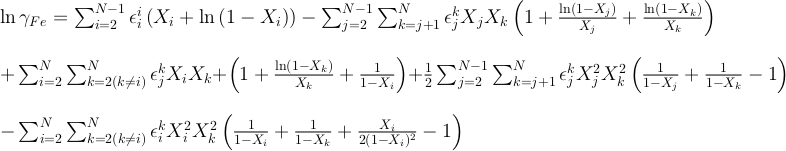
and
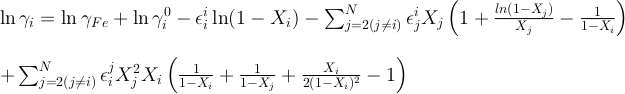
Values of εji scale with temperature following:
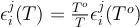
To our knowledge, there is currently no existing values of ln γOK, ln γOU, εKK or εUU in the literature. As previously assumed for other elements in such cases (e.g., Cr, Ge, Ga, W, Mo; Siebert et al., 2011), we considered ideal the activity of K and U infinitely diluted in liquid iron (i.e. γOU and γOK equal to 1) and neglected the εKK and εUU interaction parameters. We report the calculated values for all the parameters in the main text.
The oxygen fugacity in each run was measured and expressed relative to the iron-wüstite buffer according to:
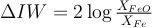
with XFeO and XFe the molar fraction of FeO in the silicate and Fe in the metal, respectively. As previously observed in experiments using basaltic or pyrolitic compositions (Siebert et al., 2012; Fischer et al., 2015), all our data fall within a narrow range of oxygen fugacity comprising between IW-0.5 and IW-1.
Literature data and current dataset
The currently published dataset consists of: Chabot and Drake (1999); Gessmann and Wood (2002); Murthy et al. (2003); Wheeler et al. (2006); Bouhifd et al. (2007); Corgne et al. (2007); Malavergne et al. (2007); Bouhifd et al. (2013); Watanabe et al. (2014); Chidester et al. (2017).
The presence of sulphur in the metal phase is known to result in the incorporation of oxygen, even at low P-T, in large volume press experiments (e.g., Gessmann and Wood, 2002; Kiseeva and Wood, 2013; Blanchard et al., 2015). Since both O and S are known to influence metal-silicate partitioning of elements, we dismissed all low P-T literature data where metal contained sulphur and where oxygen concentration wasn’t measured.
Moreover, we ruled out data involving liquid-metal, solid-silicate equilibrium, irrelevant to magma ocean conditions; and only considered data involving liquid-metal, liquid-silicate partitioning.
Large volume press experiments showed that DK increases with decreasing degree of silicate melt polymerisation (Gessmann and Wood, 2002; Murthy et al., 2003). Therefore, we only used LVP data for which the composition is either close to basalt or pyrolite. We excluded runs containing K-rich silicate (Watanabe et al., 2014) or the ones that contain very large amounts of Al2O3 or SiO2 (Gessmann and Wood, 2002; Bouhifd et al., 2007) and only considered data from Corgne et al. (2007).
Table S-6 lists all the data from the literature that have been used in this study, and combined with our data.
Metal-silicate partitioning
The results of this work draw a new picture of the partitioning of potassium and uranium between metal and silicate.
Previous studies of uranium partitioning have proposed a strong interaction with sulphur dissolved in the metal (Wheeler et al., 2006; Malavergne et al., 2007; Bouhifd et al., 2013; Chidester et al., 2017), which is not found here. Instead, we find a strong interaction with oxygen. Sulphur is known to entrain large amounts of oxygen in the metal phase, even at low pressures where oxygen doesn’t dissolve in the metal on its own (e.g., Gessmann and Wood, 2002; Kiseeva and Wood, 2013; Blanchard et al., 2015). It is thus difficult to disentangle the effects of O and S on the partitioning of elements in low pressure experiments (Blanchard et al., 2015). The LH-DAC dataset is unique in the sense that experiments can be carried out with large amounts of oxygen in the metal, due to its enhanced solubility at very high temperature, without any sulphur. This allows us to determine unambiguously the effect of O on partitioning. Add to that a number of LH-DAC experiments with S-bearing metal, and both effects can be discriminated and fitted with virtually no cross-correlation.
The work of Chidester et al. (2017) proposed that the SiO2 content of the silicate has a measurable effect on the partitioning of uranium, despite the fact that their experiments were performed with a pyrolite composition with a very narrow range of SiO2 concentrations. When comparing our basalt data with the pyrolite data of Chidester et al. (2017), we observe that samples with similar oxygen contents in the metal have very close KD values, despite a huge difference in silicate composition. Moreover, our two series of experiments with basalt and pyrolite span a large compositional range (29 to 41 wt. % SiO2), and show no dependence on SiO2 content, or even on the degree of polymerisation of the silicate framework. As noted already in Chidester et al. (2017), uranium in the silicate at those P-T and redox conditions has a +2 valence. Our observation is an indirect confirmation of this observation, as no silicate compositional effects are expected on the metal-silicate partitioning of +2 cations (Siebert et al., 2011).
In the case of potassium, most LVP studies involved S-rich metal (Gessmann and Wood, 2002; Murthy et al., 2003; Bouhifd et al., 2007), which as previously mentioned, also increases the O concentration in the metal. Unfortunately, these O concentrations weren’t measured and were assumed to be zero, which biases the thermodynamic models and attributes all the interaction effects of O to S. Moreover, the data by Watanabe et al. (2014) involved a subsolidus equilibrium between metal and orthoclase, which seems irrelevant for core formation both compositionally and structurally. Therefore, we only combined our data with that of Corgne et al. (2007) which has S-free metal, hence avoiding any artefacts due to S-O interactions.
Calculation of coefficients from equations 3, 4 and S-3, S-4
We carried out a stepwise regression where at first all the parameters were fitted simultaneously. Then the interaction parameters (εji) that were found to be statistically insignificant were set to 0, and the remaining parameters were regressed a second time. Then, the epsilon values were fixed at their nominal fitted value, and a, b, and c were fitted a third time. The b parameter was found to be statistically irrelevant for K, also the c parameter for U. These were fixed to 0, and the remaining two thermodynamic parameters were regressed one last time. The final results below are fully consistent with the initial simultaneous fit of all the parameters, but the uncertainties are propagated differently and are more statistically meaningful with the procedure used here.
Radiogenic heating
Potassium and uranium are the main sources of heat in the Earth, with 40K, 235U and 238U having a half-life of 1.24 Gyr, 703 Myr and 4.47 Gyr, respectively. Nowadays, 40K represents 0.0117 % of all potassium, but its isotopic abundance 4.56 Gyr ago represented 0.13 % of K. Similarly, uranium 238U and 235U isotopic abundances were calculated from their present value to that 4.56 Gyr ago, with 235U representing 8.5 % of total uranium. The heat production of these elements is: 29.7, 95, and 568 µW/kg for 40K, 238U and 235U, respectively (Dye, 2012).
Core formation modelling
Concentrations of both potassium and uranium in the mantle and the core were calculated following the model of Badro et al. (2015). Core formation was modelled as a multi-stage process occurring during accretion, in a terrestrial magma ocean. The Earth, which is covered by a magma ocean, grows by accretion, during which the molten metal of the accretionary material separates from the molten silicate. The metal sinks to the base of the magma ocean, acquires a particular composition by equilibrating with the surrounding magma ocean, and is then transported to the core through the solid mantle with no (or little) further equilibration. At the end of accretion, the core and mantle have acquired a certain composition, which is the integral of this process.
The multi-stage model was discretised in 1000 steps, each bringing an additional 0.1 % total Earth mass influx to the proto-Earth. At each step, the Earth grows larger, the magma ocean grows deeper, and its pressure and temperature increase, and its composition changes because of the mass influx. All these parameters are used to calculate metal-silicate partition coefficients, in turn used to calculate element concentrations in the metal and silicate. These are then used to calculate the integral path and the final composition of the core and mantle. The concentration of Ni, Co, V and Cr are used to constrain the range of core formation conditions that satisfy mantle abundance in those elements. Oxygen concentrations in the core were also calculated and used to compute the activity of uranium which strongly depends on it.
We explored all possible magma ocean depths (from 0 to 100 % of the mantle), all possible geotherms relevant to the base of that magma ocean (temperatures between the mantle solidus and liquidus), and magma ocean compositions spanning 4 orders of magnitudes in oxygen fugacity and covering the entire range of the cosmochemically observed compositional range for planetary building blocks (ordinary, carbonaceous, and enstatite chondrites).
The concentration of potassium and uranium in the bulk silicate Earth was fixed at 240 ppm and 20 ppb, respectively (McDonough and Sun, 1995).
Table S-1 Composition of starting materials. The basalt and Met 1 have been measured by EPMA, whereas the pyrolite has been measured using EDX. Fe is Alfa Aesar spherical iron powder (stock number 00170). N stands for the number of analyses that have been carried.
| Starting material | Basalt | Pyrolite | Met 1 | Fe | ||
| wt. % | N = 17 | N = 12 | N = 15 | |||
| Na2O | 2.34 (0.01) | - | Fe | 64.44 (0.81) | > 99.9 | |
| SiO2 | 35.62 (0.05) | 44.22 (0.1) | S | 15.63 (0.38) | - | |
| MgO | 10.26 (0.09) | 35.38 (0.11) | O | 1.55 (0.19) | - | |
| Al2O3 | 12.31 (0.03) | 4.33 (0.02) | ||||
| P2O5 | 0.13 (0.01) | - | ||||
| SO2 | 0.69 (0.01) | - | ||||
| K2O | 5.68 (0.03) | 4.05 (0.03) | ||||
| TiO2 | 1.32 (0.01) | - | ||||
| FeO | 17.78 (0.06) | 6.85 (0.16) | ||||
| UO2 | 2.22 (0.11) | 0.76 (0.05) | ||||
| CaO | 7.44 (0.02) | 3.14 (0.03) | ||||
| Total | 98.84 (0.08) | 100 | | | 95.83 (0.19) | 100 |
Table S-2 Experimental conditions. Pressure has been corrected for thermal pressure following Siebert et al. (2012). Oxygen fugacity of each run has been calculated relative to the IW buffer using an ideal model assuming the activity of iron in metal and silicate is 1. The estimated uncertainties for temperatures and pressures are ±150 K and ±5 GPa respectively (e.g., Fiquet et al., 2010; Siebert et al., 2012).
| Run # | T (K) | P (GPa) | ΔIW | Starting composition |
| BAS K 52 | 3600 | 62 | -0.586 | Basalt + Met 1 |
| BAS K Fe 40 | 3500 | 49 | -0.861 | Basalt + Fe |
| BAS K Fe 60 | 3700 | 70 | -0.633 | Basalt + Fe |
| BAS K Fe 70 | 4000 | 81 | -0.711 | Basalt + Fe |
| PYR K FeS 40 | 3700 | 49 | -0.82 | Pyrolite + Met 1 |
| PYR K FeS 60 | 4000 | 71 | -0.95 | Pyrolite + Met 1 |
| PYR K Fe 40 | 4000 | 54 | -1.01 | Pyrolite + Fe |
| PYR K Fe 50 | 3800 | 60 | -0.923 | Pyrolite + Fe |
| PYR K Fe 60 | 4100 | 71 | -0.75 | Pyrolite + Fe |
Table S-3 Composition of the metallic phases. *Totals include Cu, Zn, Mn and Pb which are not reported here. N stands for the number of analyses that have been performed.
| Run # | BAS K 52 | BAS K Fe 40 | BAS K Fe 60 | BAS K Fe 70 | PYR K Fe 40 | PYR K FeS 60 | PYR K FeS 40 | PYR K Fe 50 | PYR K Fe 60 |
| EPMA (wt. %) | N = 3 | N = 8 | N = 3 | N = 2 | N = 5 | N = 3 | N = 4 | N = 2 | N = 4 |
| O | 10.17 (0.11) | 6.79 (0.55) | 10.41 (0.06) | 12.11 (0.02) | 9.14 (0.51) | 9.20 (0.56) | 7.73 (0.57) | 10.54 (0.39) | 12.38 (0.25) |
| Mg | 0.34 (0.01) | 0.24 (0.01) | 0.29 (0.02) | 0.82 (0.06) | 1.18 (0.06) | 0.78 (0.43) | 0.56 (0.08) | 1.13 (0.42) | 1.03 (0.03) |
| Al | 0.26 (0.01) | 0.15 (0.02) | 0.28 (0.01) | 1.16 (0.17) | 0.16 (0.02) | 0.08 (0.03) | 0.07 (0.02) | 0.17 (0.04) | 0.13 (0.01) |
| Si | 1.43 (0.02) | 1.10 (0.16) | 1.23 (0.001) | 2.71 (0.23) | 5.78 (0.54) | 1.60 (0.09) | 1.74 (0.35) | 3.12 (0.14) | 3.45 (0.06) |
| P | 0.43 (0.01) | 0.60 (0.03) | 0.19 (0.02) | 0.17 (0.02) | - | - | - | - | - |
| S | 8.76 (0.09) | 4.13 (0.13) | 8.08 (0.04) | 10.39 (0.03) | - | 4.12 (0.05) | 5.19 (0.07) | - | - |
| K | 0.211 (0.001) | 0.10 (0.003) | 0.24 (0.01) | 0.67 (0.04) | 0.21 (0.11) | 0.47 (0.23) | 0.14 (0.01) | 0.24 (0.01) | 0.31 (0.01) |
| Ca | 0.107 (0.001) | 0.06 (0.01) | 0.07 (0.003) | 0.26 (0.01) | - | - | - | - | - |
| Ti | 0.34 (0.03) | 0.14 (0.03) | 0.24 (0.02) | 0.27 (0.07) | - | - | - | - | - |
| Fe | 71.09 (0.82) | 77.19 (0.89) | 70.11 (0.65) | 66.87 (0.46) | 77.76 (1.99) | 73.87 (0.40) | 73.61 (1.10) | 75.74 (0.01) | 76.29 (0.26) |
| U | 0.05 (0.01) | 0.03 (0.01) | 0.05 (0.004) | 0.07 (0.01) | 0.20 (0.04) | 0.31 (0.03) | 0.13 (0.04) | 0.41 (0.01) | 0.57 (0.01) |
| Total* | 96.61 (1.03) | 93.37 (0.35) | 94.07 (0.44) | 98.09 (0.39) | 97.80 (1.32) | 98.45 (1.57) | 96.54 (0.58) | 97.53 (0.93) | 99.39 (0.35) |
Table S-4 Composition of the metallic phase given as mol. %. N stands for the number of analyses that have been performed.
| Run # | BAS K 52 | BAS K Fe 40 | BAS K Fe 60 | BAS K Fe 70 | PYR K Fe 40 | PYR K FeS 60 | PYR K FeS 40 | PYR K Fe 50 | PYR K Fe 60 |
| Mol. % | N = 3 | N = 8 | N = 3 | N=2 | N = 5 | N = 3 | N = 4 | N = 2 | N = 4 |
| K | 0.23 | 0.12 | 0.27 | 0.68 | 0.23 | 0.53 | 0.17 | 0.26 | 0.33 |
| Fe | 54.73 | 67.42 | 55.03 | 47.53 | 60.99 | 58.9 | 61.17 | 59.39 | 56.85 |
| U | 0.009 | 0.007 | 0.008 | 0.012 | 0.037 | 0.059 | 0.025 | 0.075 | 0.099 |
| O | 27.31 | 20.71 | 28.52 | 30.03 | 25.02 | 25.59 | 22.42 | 28.85 | 32.19 |
| S | 11.75 | 6.29 | 11.04 | 12.86 | 0 | 5.72 | 7.51 | 0 | 0 |
| Si | 2.18 | 1.91 | 1.91 | 3.83 | 9.01 | 2.54 | 2.88 | 4.87 | 5.11 |
Table S-5 Compositions of silicate phases. N stands for the number of analyses that have been performed.
| Run # | BAS K 52 | BAS K Fe 40 | BAS K Fe 60 | BAS K Fe 70 | PYR K Fe 40 | PYR K FeS 60 | PYR K FeS 40 | PYR K Fe 50 | PYR K Fe 60 |
| EPMA (wt. %) | N = 3 | N = 3 | N = 3 | N = 3 | N = 6 | N = 6 | N = 5 | N = 4 | N = 5 |
| Na2O | 2.03 (0.03) | 3.06 (0.13) | 2.18 (0.04) | 2.25 (0.14) | - | - | - | - | - |
| SiO2 | 29.65 (0.28) | 33.26 (1.09) | 30.14 (0.28) | 33.08 (0.70) | 40.81 (2.78) | 31.64 (0.71) | 34.13 (0.74) | 32.78 (0.55) | 33.67 (2.38) |
| MgO | 7.03 (0.08) | 8.59 (0.37) | 6.53 (0.10) | 7.06 (0.13) | 27.78 (2.36) | 21.02 (0.46) | 20.75 (0.39) | 21.57 (0.67) | 21.71 (2.31) |
| Al2O3 | 9.24 (0.15) | 10.07 (0.42) | 10.75 (0.16) | 12.31 (0.28) | 4.45 (0.46) | 3.43 (0.13) | 3.29 (0.04) | 4.01 (0.14) | 3.31 (0.42) |
| P2O5 | 0.21 (0.05) | 0.21 (0.11) | 0.19 (0.07) | 0.19 (0.04) | - | - | - | - | - |
| SO2 | 1.44 (0.12) | 0.26 (0.16) | 1.10 (0.09) | 1.13 (0.16) | - | 0.24 (0.04) | 0.60 (0.27) | - | - |
| K2O | 5.57 (0.14) | 6.17 (0.16) | 6.35 (0.06) | 6.32 (0.12) | 6.54 (0.86) | 10.66 (1.66) | 6.52 (0.12) | 8.51 (0.26) | 8.00 (1.64) |
| TiO2 | 1.58 (0.04) | 1.40 (0.05) | 1.39 (0.05) | 1.44 (0.01) | - | - | - | - | - |
| FeO | 33.12 (0.54) | 29.29 (1.23) | 32.94 (0.59) | 28.59 (1.13) | 25.79 (7.05) | 24 78 (1.09) | 28.17 (1.72) | 25.88 (1.32) | 28.65 (5.27) |
| CuO | 0.70 (0.11) | 0.56 (0.13) | 1.14 (0.26) | 0.81 (0.19) | 1.42 (0.21) | 3.19 (0.22) | 2.53 (0.28) | 2.53 (0.13) | 2.50 (0.43) |
| ZnO | 2.85 (0.07) | 3.04 (0.10) | 2.78 (0.05) | 2.85 (0.05) | 0.36 (0.06) | 0.67 (0.08) | 0.48 (0.04) | 0.46 (0.06) | 0.55 (0.06) |
| UO2 | 0.25 (0.02) | 0.31 (0.04) | 0.19 (0.02) | 0.25 (0.05) | 0.97 (0.06) | 1.10 (0.10) | 1.10 (0.07) | 0.96 (0.09) | 1.99 (0.17) |
| PbO | 0.57 (0.04) | 0.40 (0.05) | 0.49 (0.03) | 0.40 (0.04) | - | - | - | - | - |
| CaO | 2.67 (0.06) | 3.13 (0.07) | 1.90 (0.01) | 2.52 (0.07) | 2.59 (0.28) | 2.64 (0.05) | 3.03 (0.10) | 2.87 (0.10) | 3.16 (0.28) |
| MnO | 0.23 (0.06) | 0.17 (0.03) | 0.21 (0.04) | 0.19 (0.03) | - | - | - | - | - |
| Total | 97.92 (0.96) | 99.94 (0.58) | 98.29 (0.25) | 99.40 (0.24) | 110.75 (1.17) | 99.66 (1.62) | 101.10 (0.99) | 99.62 (1.04) | 103.62 (0.28) |
Table S-6 Literature data that have been used along with our data to perform thermodynamic regression.
| Reference | Run# | Reference | Run# | |
| Potassium | Uranium | |||
| Corgne et al., 2007 | PC509 | Wheeler et al., 2006 | PC408 | |
| Corgne et al., 2007 | PC504 | Malavergne et al., 2007 | #2309 | |
| Corgne et al., 2007 | PC508 | Malavergne et al., 2007 | #414 | |
| Corgne et al., 2007 | PC514 | Bouhifd et al., 2013 | 969 | |
| Corgne et al., 2007 | PC515 | Bouhifd et al., 2013 | 975 | |
| Corgne et al., 2007 | PR380 | Bouhifd et al., 2013 | 1027 | |
| Corgne et al., 2007 | PR381 | Bouhifd et al., 2013 | 1022 | |
| Corgne et al., 2007 | PR382 | Bouhifd et al., 2013 | 986 | |
| Corgne et al., 2007 | PR390 | Chidester et al., 2017 | B22 | |
| Corgne et al., 2007 | PR394 | Chidester et al., 2017 | B23 | |
| Corgne et al., 2007 | PR395 | Chidester et al., 2017 | B42 | |
| Chidester et al., 2017 | B56 | |||
| Chidester et al., 2017 | B50 | |||
| Chidester et al., 2017 | B66 | |||
| | | | Chidester et al., 2017 | B49 |
Figure S-1 Backscattered scanning electron microscopy (FEG-SEM) image of a typical recovered sample. Samples are excavated from the melted region, thinned down to a thickness of ~3 microns, and welded to a TEM grid using a FIB instrument. The metal and silicate phases are analysed by electron microprobe analysis.
Figure S-2 Comparison of equilibrium constant (log K) and the exchange coefficient (log KD) for potassium (a) and uranium (b) metal-silicate exchange reactions. The difference between log(K) and log(KD) is the activity coefficient ratio
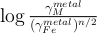. While activities are limited for potassium (a), because all interaction parameters are 0, they are obvious in uranium (b) because of a large interaction parameter between U and O in the metal.Supplementary Information References
Andrault, D., Bolfan-Casanova, N., Nigro, G.L., Bouhifd, M.A., Garbarino, G., Mezouar, M. (2011) Solidus and liquidus profiles of chondritic mantle: Implication for melting of the Earth across its history. Earth and Planetary Science Letters 304, 251–259.
Auzende, A.L., Gillot, J., Coquet, A., Hennet, L., Ona-Nguema, G., Bonnin, D., Esteve, I., Roskosz, M., Fiquet, G. (2011) Synthesis of amorphous MgO-rich peridotitic starting material for laser-heated diamond anvil cell experiments–application to iron partitioning in the mantle. High Pressure Research 31, 199–213.
Badro, J., Brodholt, J.P., Piet, H., Siebert, J., Ryerson, F.J. (2015) Core formation and core composition from coupled geochemical and geophysical constraints. Proceedings of the National Academy of Sciences 112, 12310–12314.
Benedetti, L.R., Loubeyre, P. (2004) Temperature gradients, wavelength-dependent emissivity, and accuracy of high and very-high temperatures measured in the laser-heated diamond cell. High Pressure Research 24, 423–445.
Bouhifd, M.A., Gautron, L., Bolfan-Casanova, N., Malavergne, V., Hammouda, T., Andrault, D., Jephcoat, A.P. (2007) Potassium partitioning into molten iron alloys at high-pressure: Implications for Earth's core. Physics of the Earth and Planetary Interiors 160, 22–33.
Bouhifd, M.A., Andrault, D., Bolfan-Casanova, N., Hammouda, T., Devidal, J.L. (2013) Metal–silicate partitioning of Pb and U: Effects of metal composition and oxygen fugacity. Geochimica et Cosmochimica Acta 114, 13–28.
Blanchard, I., Badro, J., Siebert, J., Ryerson, F.J. (2015) Composition of the core from gallium metal–silicate partitioning experiments. Earth and Planetary Science Letters 427, 191–201.
Chabot, N.L., Drake, M.J. (1999) Potassium solubility in metal: the effects of composition at 15 kbar and 1900 C on partitioning between iron alloys and silicate melts. Earth and Planetary Science Letters 172, 323–335.
Corgne, A., Keshav, S., Fei, Y., McDonough, W.F. (2007) How much potassium is in the Earth's core? New insights from partitioning experiments? Earth and Planetary Science Letters 256, 567–576.
Chidester, B.A., Rahman, Z., Righter, K., Campbell, A.J. (2017) Metal–silicate partitioning of U: Implications for the heat budget of the core and evidence for reduced U in the mantle. Geochimica et Cosmochimica Acta 199, 1–12.
Dye, S.T. (2012) Geoneutrinos and the radioactive power of the Earth. Reviews of Geophysics 50, RG3007, doi: 10.1029/2012RG000400.
Fischer, R.A., Nakajima, Y., Campbell, A.J., Frost, D.J., Harries, D., Langenhorst, F., Miyajima, N., Pollok, K., Rubie, D.C. (2015) High pressure metal–silicate partitioning of Ni, Co, V, Cr, Si, and O. Geochimica et Cosmochimica Acta 167, 177–194.
Fiquet, G., Auzende, A.L., Siebert, J., Corgne, A., Bureau, H., Ozawa, H., Garbarino, G. (2010) Melting of peridotite to 140 gigapascals. Science 329, 1516–1518.
Gessmann, C.K., Wood, B.J. (2002) Potassium in the Earth’s core? Earth and Planetary Science Letters 200, 63–78.
Kiseeva, E.S., Wood, B.J. (2013) A simple model for chalcophile element partitioning between sulphide and silicate liquids with geochemical applications. Earth and Planetary Science Letters 383, 68–81.
Ma, Z. (2001) Thermodynamic description for concentrated metallic solutions using interaction parameters. Metallurgical and Materials Transactions B 32, 87–103.
McDonough, W.F., Sun, S.S. (1995) The composition of the Earth. Chemical Geology 120, 223–253.
Murthy, V.R., Van Westrenen, W., Fei, Y. (2003) Experimental evidence that potassium is a substantial radioactive heat source in planetary cores. Nature 423, 163–165.
Malavergne, V., Tarrida, M., Combes, R., Bureau, H., Jones, J., Schwandt, C. (2007) New high-pressure and high-temperature metal/silicate partitioning of U and Pb: Implications for the cores of the Earth and Mars. Geochimica et Cosmochimica Acta 71, 2637–2655.
Siebert, J., Corgne, A., Ryerson, F.J. (2011) Systematics of metal–silicate partitioning for many siderophile elements applied to Earth’s core formation. Geochimica et Cosmochimica Acta 75, 1451–1489.
Siebert, J., Badro, J., Antonangeli, D., Ryerson, F.J. (2012) Metal–silicate partitioning of Ni and Co in a deep magma ocean. Earth and Planetary Science Letters 321, 189–197.
Siebert, J., Badro, J., Antonangeli, D., Ryerson, F.J. (2013) Terrestrial accretion under oxidizing conditions. Science 339, 1194–1197.
Thibault, Y., Walter, M.J. (1995) The influence of pressure and temperature on the metal-silicate partition coefficients of nickel and cobalt in a model C1 chondrite and implications for metal segregation in a deep magma ocean. Geochimica et Cosmochimica Acta 59, 991–1002.
Wheeler, K.T., Walker, D., Fei, Y., Minarik, W.G., McDonough, W.F. (2006) Experimental partitioning of uranium between liquid iron sulfide and liquid silicate: Implications for radioactivity in the Earth’s core. Geochimica et Cosmochimica Acta 70, 1537–1547.
Watanabe, K., Ohtani, E., Kamada, S., Sakamaki, T., Miyahara, M., Ito, Y. (2014) The abundance of potassium in the Earth’s core. Physics of the Earth and Planetary Interiors 237, 65–72.
Figures and Tables
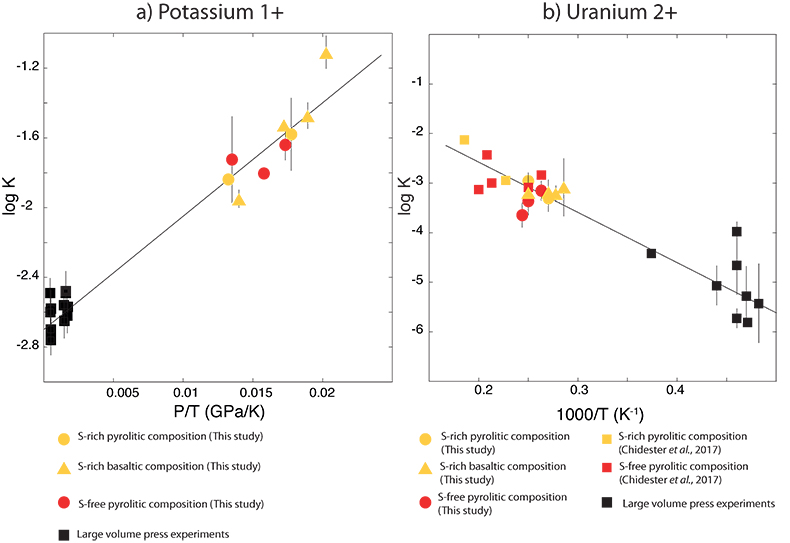
Figure 1 Thermodynamic models of K and U partitioning between metal and silicate. (a) Equilibrium constant for potassium metal-silicate partitioning (Eq. 1) as a function of P/T. The line corresponds to the least squares fit (R2 = 0.94) of the thermodynamic model (Eq. 3) with a = -2.7 ± 0.03 and c = 65 ± 2.5. (b) Equilibrium constant of uranium metal-silicate partitioning (Eq. 2) as a function of the reciprocal temperature. The line corresponds to the least squares fit (R2 = 0.91) of the thermodynamic model (Eq. 4) with a = -0.55 ± 0.21, b = -10133 ± 642 and εUO = -31.
Table 1 Coefficients from Eqs. 3, 4 (and S-3, S-4) obtained by least squares linear regression of the experimental data, along with their associated (1 sigma) uncertainties. Details of the calculation are given in the Supplementary Information.
| Element i | a | b (K) | c (K/GPa) | εOi (1873 K) | εSi (1873 K) | εSii (1873 K) |
| Potassium | –2.7 (0.03) | 0 | 65 (2.5) | 0 | 0 | 0 |
| Uranium | –0.55 (0.21) | –10133 (642) | 0 | –31 | 0 | 0 |
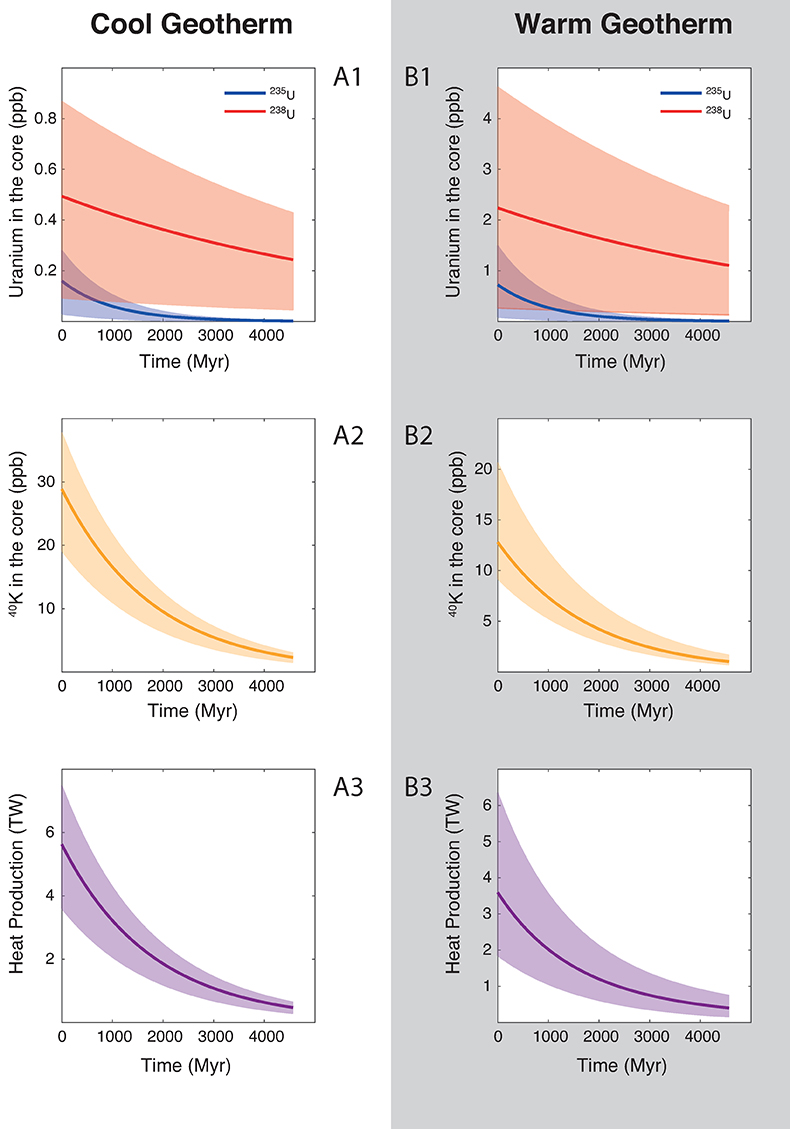
Figure 2 Concentration of K and U in the core from continuous core-formation models, assuming two magma ocean geotherms: cool (A1,2,3) and warm (B1,2,3). The top panel is the abundance of 238U and 235U as a function of time, the middle panel corresponds to that of 40K as a function of time, and the bottom panel is the total power produced in the core by the radioactive decay of these three radionuclides over time.
Back to article
Supplementary Figures and Tables
Table S-1 Composition of starting materials. The basalt and Met 1 have been measured by EPMA, whereas the pyrolite has been measured using EDX. Fe is Alfa Aesar spherical iron powder (stock number 00170). N stands for the number of analyses that have been carried.
| Starting material | Basalt | Pyrolite | Met 1 | Fe | ||
| wt. % | N = 17 | N = 12 | N = 15 | |||
| Na2O | 2.34 (0.01) | - | Fe | 64.44 (0.81) | > 99.9 | |
| SiO2 | 35.62 (0.05) | 44.22 (0.1) | S | 15.63 (0.38) | - | |
| MgO | 10.26 (0.09) | 35.38 (0.11) | O | 1.55 (0.19) | - | |
| Al2O3 | 12.31 (0.03) | 4.33 (0.02) | ||||
| P2O5 | 0.13 (0.01) | - | ||||
| SO2 | 0.69 (0.01) | - | ||||
| K2O | 5.68 (0.03) | 4.05 (0.03) | ||||
| TiO2 | 1.32 (0.01) | - | ||||
| FeO | 17.78 (0.06) | 6.85 (0.16) | ||||
| UO2 | 2.22 (0.11) | 0.76 (0.05) | ||||
| CaO | 7.44 (0.02) | 3.14 (0.03) | ||||
| Total | 98.84 (0.08) | 100 | | | 95.83 (0.19) | 100 |
Table S-2 Experimental conditions. Pressure has been corrected for thermal pressure following Siebert et al. (2012). Oxygen fugacity of each run has been calculated relative to the IW buffer using an ideal model assuming the activity of iron in metal and silicate is 1. The estimated uncertainties for temperatures and pressures are ±150 K and ±5 GPa respectively (e.g., Fiquet et al., 2010; Siebert et al., 2012).
| Run # | T (K) | P (GPa) | ΔIW | Starting composition |
| BAS K 52 | 3600 | 62 | -0.586 | Basalt + Met 1 |
| BAS K Fe 40 | 3500 | 49 | -0.861 | Basalt + Fe |
| BAS K Fe 60 | 3700 | 70 | -0.633 | Basalt + Fe |
| BAS K Fe 70 | 4000 | 81 | -0.711 | Basalt + Fe |
| PYR K FeS 40 | 3700 | 49 | -0.82 | Pyrolite + Met 1 |
| PYR K FeS 60 | 4000 | 71 | -0.95 | Pyrolite + Met 1 |
| PYR K Fe 40 | 4000 | 54 | -1.01 | Pyrolite + Fe |
| PYR K Fe 50 | 3800 | 60 | -0.923 | Pyrolite + Fe |
| PYR K Fe 60 | 4100 | 71 | -0.75 | Pyrolite + Fe |
Table S-3 Composition of the metallic phases. *Totals include Cu, Zn, Mn and Pb which are not reported here. N stands for the number of analyses that have been performed.
| Run # | BAS K 52 | BAS K Fe 40 | BAS K Fe 60 | BAS K Fe 70 | PYR K Fe 40 | PYR K FeS 60 | PYR K FeS 40 | PYR K Fe 50 | PYR K Fe 60 |
| EPMA (wt. %) | N = 3 | N = 8 | N = 3 | N = 2 | N = 5 | N = 3 | N = 4 | N = 2 | N = 4 |
| O | 10.17 (0.11) | 6.79 (0.55) | 10.41 (0.06) | 12.11 (0.02) | 9.14 (0.51) | 9.20 (0.56) | 7.73 (0.57) | 10.54 (0.39) | 12.38 (0.25) |
| Mg | 0.34 (0.01) | 0.24 (0.01) | 0.29 (0.02) | 0.82 (0.06) | 1.18 (0.06) | 0.78 (0.43) | 0.56 (0.08) | 1.13 (0.42) | 1.03 (0.03) |
| Al | 0.26 (0.01) | 0.15 (0.02) | 0.28 (0.01) | 1.16 (0.17) | 0.16 (0.02) | 0.08 (0.03) | 0.07 (0.02) | 0.17 (0.04) | 0.13 (0.01) |
| Si | 1.43 (0.02) | 1.10 (0.16) | 1.23 (0.001) | 2.71 (0.23) | 5.78 (0.54) | 1.60 (0.09) | 1.74 (0.35) | 3.12 (0.14) | 3.45 (0.06) |
| P | 0.43 (0.01) | 0.60 (0.03) | 0.19 (0.02) | 0.17 (0.02) | - | - | - | - | - |
| S | 8.76 (0.09) | 4.13 (0.13) | 8.08 (0.04) | 10.39 (0.03) | - | 4.12 (0.05) | 5.19 (0.07) | - | - |
| K | 0.211 (0.001) | 0.10 (0.003) | 0.24 (0.01) | 0.67 (0.04) | 0.21 (0.11) | 0.47 (0.23) | 0.14 (0.01) | 0.24 (0.01) | 0.31 (0.01) |
| Ca | 0.107 (0.001) | 0.06 (0.01) | 0.07 (0.003) | 0.26 (0.01) | - | - | - | - | - |
| Ti | 0.34 (0.03) | 0.14 (0.03) | 0.24 (0.02) | 0.27 (0.07) | - | - | - | - | - |
| Fe | 71.09 (0.82) | 77.19 (0.89) | 70.11 (0.65) | 66.87 (0.46) | 77.76 (1.99) | 73.87 (0.40) | 73.61 (1.10) | 75.74 (0.01) | 76.29 (0.26) |
| U | 0.05 (0.01) | 0.03 (0.01) | 0.05 (0.004) | 0.07 (0.01) | 0.20 (0.04) | 0.31 (0.03) | 0.13 (0.04) | 0.41 (0.01) | 0.57 (0.01) |
| Total* | 96.61 (1.03) | 93.37 (0.35) | 94.07 (0.44) | 98.09 (0.39) | 97.80 (1.32) | 98.45 (1.57) | 96.54 (0.58) | 97.53 (0.93) | 99.39 (0.35) |
Table S-4 Composition of the metallic phase given as mol. %. N stands for the number of analyses that have been performed.
| Run # | BAS K 52 | BAS K Fe 40 | BAS K Fe 60 | BAS K Fe 70 | PYR K Fe 40 | PYR K FeS 60 | PYR K FeS 40 | PYR K Fe 50 | PYR K Fe 60 |
| Mol. % | N = 3 | N = 8 | N = 3 | N=2 | N = 5 | N = 3 | N = 4 | N = 2 | N = 4 |
| K | 0.23 | 0.12 | 0.27 | 0.68 | 0.23 | 0.53 | 0.17 | 0.26 | 0.33 |
| Fe | 54.73 | 67.42 | 55.03 | 47.53 | 60.99 | 58.9 | 61.17 | 59.39 | 56.85 |
| U | 0.009 | 0.007 | 0.008 | 0.012 | 0.037 | 0.059 | 0.025 | 0.075 | 0.099 |
| O | 27.31 | 20.71 | 28.52 | 30.03 | 25.02 | 25.59 | 22.42 | 28.85 | 32.19 |
| S | 11.75 | 6.29 | 11.04 | 12.86 | 0 | 5.72 | 7.51 | 0 | 0 |
| Si | 2.18 | 1.91 | 1.91 | 3.83 | 9.01 | 2.54 | 2.88 | 4.87 | 5.11 |
Table S-5 Compositions of silicate phases. N stands for the number of analyses that have been performed.
| Run # | BAS K 52 | BAS K Fe 40 | BAS K Fe 60 | BAS K Fe 70 | PYR K Fe 40 | PYR K FeS 60 | PYR K FeS 40 | PYR K Fe 50 | PYR K Fe 60 |
| EPMA (wt. %) | N = 3 | N = 3 | N = 3 | N = 3 | N = 6 | N = 6 | N = 5 | N = 4 | N = 5 |
| Na2O | 2.03 (0.03) | 3.06 (0.13) | 2.18 (0.04) | 2.25 (0.14) | - | - | - | - | - |
| SiO2 | 29.65 (0.28) | 33.26 (1.09) | 30.14 (0.28) | 33.08 (0.70) | 40.81 (2.78) | 31.64 (0.71) | 34.13 (0.74) | 32.78 (0.55) | 33.67 (2.38) |
| MgO | 7.03 (0.08) | 8.59 (0.37) | 6.53 (0.10) | 7.06 (0.13) | 27.78 (2.36) | 21.02 (0.46) | 20.75 (0.39) | 21.57 (0.67) | 21.71 (2.31) |
| Al2O3 | 9.24 (0.15) | 10.07 (0.42) | 10.75 (0.16) | 12.31 (0.28) | 4.45 (0.46) | 3.43 (0.13) | 3.29 (0.04) | 4.01 (0.14) | 3.31 (0.42) |
| P2O5 | 0.21 (0.05) | 0.21 (0.11) | 0.19 (0.07) | 0.19 (0.04) | - | - | - | - | - |
| SO2 | 1.44 (0.12) | 0.26 (0.16) | 1.10 (0.09) | 1.13 (0.16) | - | 0.24 (0.04) | 0.60 (0.27) | - | - |
| K2O | 5.57 (0.14) | 6.17 (0.16) | 6.35 (0.06) | 6.32 (0.12) | 6.54 (0.86) | 10.66 (1.66) | 6.52 (0.12) | 8.51 (0.26) | 8.00 (1.64) |
| TiO2 | 1.58 (0.04) | 1.40 (0.05) | 1.39 (0.05) | 1.44 (0.01) | - | - | - | - | - |
| FeO | 33.12 (0.54) | 29.29 (1.23) | 32.94 (0.59) | 28.59 (1.13) | 25.79 (7.05) | 24 78 (1.09) | 28.17 (1.72) | 25.88 (1.32) | 28.65 (5.27) |
| CuO | 0.70 (0.11) | 0.56 (0.13) | 1.14 (0.26) | 0.81 (0.19) | 1.42 (0.21) | 3.19 (0.22) | 2.53 (0.28) | 2.53 (0.13) | 2.50 (0.43) |
| ZnO | 2.85 (0.07) | 3.04 (0.10) | 2.78 (0.05) | 2.85 (0.05) | 0.36 (0.06) | 0.67 (0.08) | 0.48 (0.04) | 0.46 (0.06) | 0.55 (0.06) |
| UO2 | 0.25 (0.02) | 0.31 (0.04) | 0.19 (0.02) | 0.25 (0.05) | 0.97 (0.06) | 1.10 (0.10) | 1.10 (0.07) | 0.96 (0.09) | 1.99 (0.17) |
| PbO | 0.57 (0.04) | 0.40 (0.05) | 0.49 (0.03) | 0.40 (0.04) | - | - | - | - | - |
| CaO | 2.67 (0.06) | 3.13 (0.07) | 1.90 (0.01) | 2.52 (0.07) | 2.59 (0.28) | 2.64 (0.05) | 3.03 (0.10) | 2.87 (0.10) | 3.16 (0.28) |
| MnO | 0.23 (0.06) | 0.17 (0.03) | 0.21 (0.04) | 0.19 (0.03) | - | - | - | - | - |
| Total | 97.92 (0.96) | 99.94 (0.58) | 98.29 (0.25) | 99.40 (0.24) | 110.75 (1.17) | 99.66 (1.62) | 101.10 (0.99) | 99.62 (1.04) | 103.62 (0.28) |
Table S-6 Literature data that have been used along with our data to perform thermodynamic regression.
| Reference | Run# | Reference | Run# | |
| Potassium | Uranium | |||
| Corgne et al., 2007 | PC509 | Wheeler et al., 2006 | PC408 | |
| Corgne et al., 2007 | PC504 | Malavergne et al., 2007 | #2309 | |
| Corgne et al., 2007 | PC508 | Malavergne et al., 2007 | #414 | |
| Corgne et al., 2007 | PC514 | Bouhifd et al., 2013 | 969 | |
| Corgne et al., 2007 | PC515 | Bouhifd et al., 2013 | 975 | |
| Corgne et al., 2007 | PR380 | Bouhifd et al., 2013 | 1027 | |
| Corgne et al., 2007 | PR381 | Bouhifd et al., 2013 | 1022 | |
| Corgne et al., 2007 | PR382 | Bouhifd et al., 2013 | 986 | |
| Corgne et al., 2007 | PR390 | Chidester et al., 2017 | B22 | |
| Corgne et al., 2007 | PR394 | Chidester et al., 2017 | B23 | |
| Corgne et al., 2007 | PR395 | Chidester et al., 2017 | B42 | |
| Chidester et al., 2017 | B56 | |||
| Chidester et al., 2017 | B50 | |||
| Chidester et al., 2017 | B66 | |||
| | | | Chidester et al., 2017 | B49 |
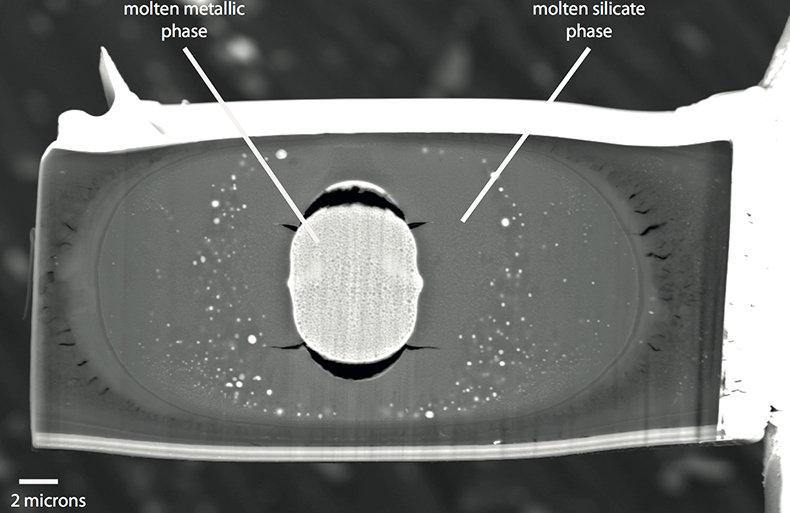
Figure S-1 Backscattered scanning electron microscopy (FEG-SEM) image of a typical recovered sample. Samples are excavated from the melted region, thinned down to a thickness of ~3 microns, and welded to a TEM grid using a FIB instrument. The metal and silicate phases are analysed by electron microprobe analysis.
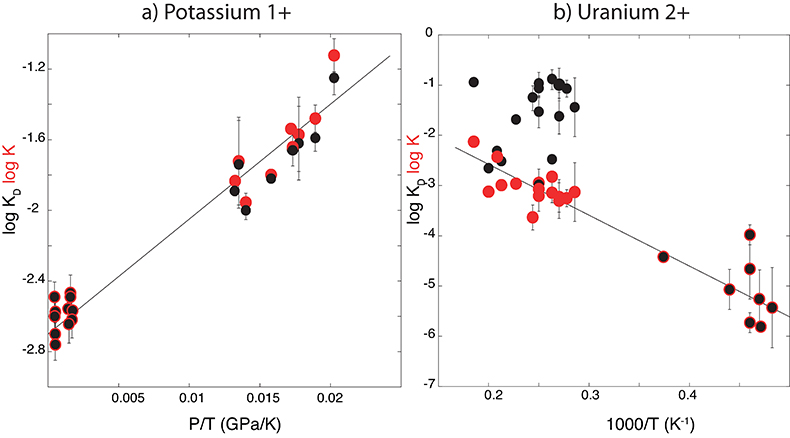
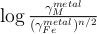Figure S-2 Comparison of equilibrium constant (log K) and the exchange coefficient (log KD) for potassium (a) and uranium (b) metal-silicate exchange reactions. The difference between log(K) and log(KD) is the activity coefficient ratio EQUATION . While activities are limited for potassium (a), because all interaction parameters are 0, they are obvious in uranium (b) because of a large interaction parameter between U and O in the metal.