Thermodynamic controls on redox-driven kinetic stable isotope fractionation
Affiliations | Corresponding Author | Cite as | Funding information
Published by the European Association of Geochemistry
under Creative Commons License CC BY-NC-ND 4.0
Keywords: isotopes, isotope fractionation, chromium, redox reactions
- Share this article
Article views:4,391Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Figures and Tables
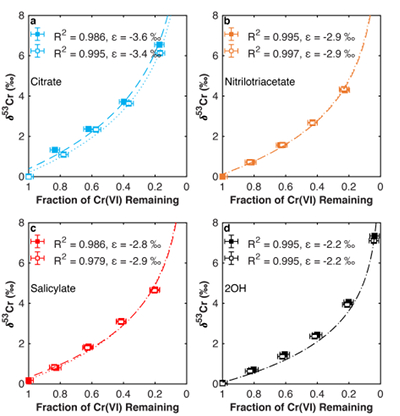 Figure 1 Isotope fractionation during Cr(VI) reduction by various aqueous Fe(II) species. Filled and open symbols in each plot show duplicate reactors. Rayleigh curves based on linear best fits are plotted as dashed lines (filled symbols) and dotted lines (open symbols). Vertical error bars (2 s.d.) are smaller than the symbols. | 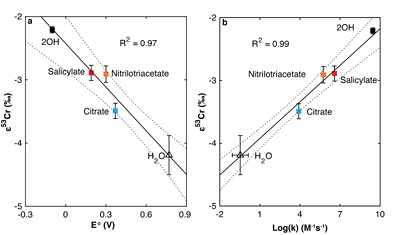 Figure 2 Linear relationships of kinetic isotope fractionation factor for Cr(VI) reduction with (a) the Fe(II)-Fe(III) standard reduction potential and (b) rate constants. Solid line shows weighted linear regression, and dotted lines show 95 % confidence interval. Each symbol shows the average fractionation factor calculated for replicate experiments. Error bars are 2 s.d. The fractionation factor for Cr(VI) reduction by Fe(H2O)62+ is taken from Kitchen et al. (2012), and the rate constants are taken from Buerge and Hug (1997, 1998). | 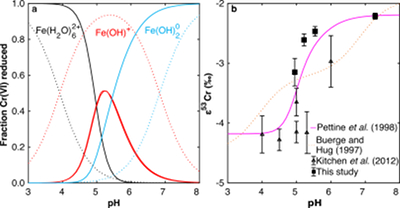 Figure 3 Effects of pH on the kinetics and isotope fractionation of Cr(VI) reduction by aqueous Fe(II). In both parts, solid lines show the model based on the rate law of Pettine et al. (1998); dashed lines show the model based on the rate law of Buerge and Hug (1997). (a) The fraction of Cr(VI) reduced by each Fe(II) species is contingent on pH-dependent Fe(II) speciation and the rate law of Cr(VI) reduction. (b) The effective fractionation factor is the weighted average of the fractionation factors for Cr(VI) reduction by each Fe(II) species. Error bars on the symbols in (b) are 2 s.d. | 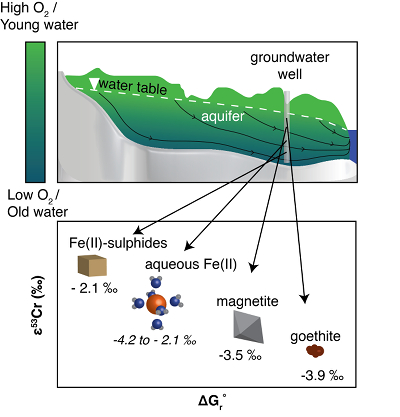 Figure 4 Schematic of Cr(VI) reduction and variations in εkin with depth, groundwater age, and oxygen levels. The dominant reductants are ordered according to their relative locations on the redox tower. Kinetic fractionation factors are taken from this study; aqueous Fe(II); Kitchen et al. (2012), aqueous Fe(II); Basu and Johnson (2012), Fe(II)-doped goethite and Fe(II) sulphide, and Ellis et al. (2002), magnetite. |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
top
Introduction
Stable isotope fractionation is used to examine Earth processes ranging from the evolution of redox conditions in ancient oceans (Frei et al., 2009
Frei, R., Gaucher, C., Poulton, S.W., Canfield, D.E. (2009) Fluctuations in Precambrian atmospheric oxygenation recorded by chromium isotopes. Nature 461, 250–253.
) to the fate of modern contaminant plumes (Ellis et al., 2002Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
). Interpreting the isotopic signatures observed in these systems requires frameworks to link fractionation to environmental variables. For instance, fractionation during precipitation can be modelled as a function of solvation energies and the composition of ions in solution or the balance between forward and backward reaction rates (Fantle and DePaolo, 2007Fantle, M.S., DePaolo, D.J. (2007) Ca isotopes in carbonate sediment and pore fluid from ODP Site 807A: The Ca2+(aq)–calcite equilibrium fractionation factor and calcite recrystallization rates in Pleistocene sediments. Geochimica et Cosmochimica Acta 71, 2524–2546.
; DePaolo, 2011DePaolo, D.J. (2011) Surface kinetic model for isotopic and trace element fractionation during precipitation of calcite from aqueous solutions. Geochimica et Cosmochimica Acta 75, 1039–1056.
; Hofmann et al., 2012Hofmann, A.E., Bourg, I.C., DePaolo, D.J. (2012) Ion desolvation as a mechanism for kinetic isotope fractionation in aqueous systems. Proceedings of the National Academy of Sciences 109, 18689–18694.
; Nielsen et al., 2012Nielsen, L.C., DePaolo, D.J., De Yoreo, J.J. (2012) Self-consistent ion-by-ion growth model for kinetic isotopic fractionation during calcite precipitation. Geochimica et Cosmochimica Acta 86, 166–181.
). Similarly, Kavner and colleagues have shown that kinetic fractionation during metal electroplating scales linearly with the standard electrode potential (E°) (Kavner et al., 2005Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
, 2008Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
). However, if the standard electrode potential is taken to be analogous to the free energy of reaction (ΔGr°) in natural soils and sediments, this relationship has not yet been demonstrated for non-electrochemical reactions.Knowledge of the thermodynamic controls on kinetic fractionation could be used to interpret redox-driven isotope fractionation in natural systems. The relationship between thermodynamic parameters (E° or ΔGr°) and the kinetics of electron transfer can be formalised via Marcus theory (Marcus, 1964
Marcus, R.A. (1964) Chemical and electrochemical electron-transfer theory. Annual Review of Physical Chemistry 15, 155–196.
, 1965Marcus, R.A. (1965) On the Theory of Electron‐Transfer Reactions. VI. Unified Treatment for Homogeneous and Electrode Reactions. The Journal of Chemical Physics 43, 679–701.
, 1993Marcus, R.A. (1993) Electron transfer reactions in chemistry. Theory and experiment. Reviews of Modern Physics 65, 599–610.
). Unlike other models that link changes in observed fractionation with shifts between kinetic and equilibrium fractionation (DePaolo, 2011DePaolo, D.J. (2011) Surface kinetic model for isotopic and trace element fractionation during precipitation of calcite from aqueous solutions. Geochimica et Cosmochimica Acta 75, 1039–1056.
), Marcus theory predicts changes in the kinetic fractionation factor itself. For most electron transfer reactions, Marcus theory predicts that the rate constant (k) should increase log-linearly as ΔGr° decreases, such that a reaction that is more thermodynamically favourable in the standard state is faster. Kavner and colleagues have shown that Marcus theory also describes kinetic isotope fractionation during redox reactions (Kavner et al., 2005Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
, 2008Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
). Specifically, Marcus theory predicts that the kinetic fractionation factor (εkin) follows a linear free energy relationship for redox reactions with similar reaction mechanisms and equilibrium fractionation factors. A reaction with a lower ΔGr° has a lower activation energy, and the difference between the activation energies of different isotopologues is also smaller. Thus, a redox reaction that is more thermodynamically favourable in the standard state is not only faster but also exhibits less kinetic fractionation.For isotope fractionation in natural systems, the combination of electron donor and acceptor determines ΔGr°. For example, as an oxidant such as Cr(VI) enters an aquifer and travels along a flow path characterised by decreasing O2 and Eh, Cr(VI) also encounters a changing series of abiotic reductants, e.g., from trace Fe(II) sorbed onto goethite to aqueous Fe(II) to Fe(II) sulphides, in broad accordance with the redox ladder (Champ et al., 1979
Champ, D.R., Gulens, J., Jackson, R.E. (1979) Oxidation–reduction sequences in ground water flow systems. Canadian Journal of Earth Sciences 16, 12–23.
). This sequence of reductants results in a shifting ΔGr° for the reduction of Cr(VI). If ΔGr° also influences k and εkin, we would expect kinetic isotope fractionation during Cr(VI) reduction to change along the flow path in a predictable fashion, consistent with electrochemical experiments. To date, the expected linear relationship between εkin and ΔGr° has not been demonstrated in natural systems.To test for a thermodynamic control on kinetic fractionation, we examined a model system, Cr(VI) reduction by aqueous Fe(II). Chromium(VI) reduction was chosen because it consistently results in kinetic isotope fractionation (Wang et al., 2015
Wang, X., Johnson, T.M., Ellis, A.S. (2015) Equilibrium isotopic fractionation and isotopic exchange kinetics between Cr(III) and Cr(VI). Geochimica et Cosmochimica Acta 153, 72–90.
) and is actively cycled in aquifers and marine sediments, even though the multi-electron reduction is more difficult to model explicitly. Chromium naturally occurs as Cr(VI), which is generally soluble and toxic, and as Cr(III), which is both far less soluble and environmentally benign (Ball and Nordstrom, 1998Ball, J.W., Nordstrom, D.K. (1998) Critical Evaluation and Selection of Standard State Thermodynamic Properties for Chromium Metal and Its Aqueous Ions, Hydrolysis Species, Oxides, and Hydroxides. Journal of Chemical & Engineering Data 43, 895–918.
). Fractionation during Cr(VI) reduction induces kinetic fractionation that enriches the remaining Cr(VI) in the heavier isotopes (Ellis et al., 2002Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
). This fractionation may be documented as positive isotopic excursions in the rock record (Ellis et al., 2002Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
; Frei et al., 2009Frei, R., Gaucher, C., Poulton, S.W., Canfield, D.E. (2009) Fluctuations in Precambrian atmospheric oxygenation recorded by chromium isotopes. Nature 461, 250–253.
). In modern environments, Cr(VI) isotope signatures may fingerprint reduction of Cr(VI) pollution (Berna et al., 2010Berna, E.C., Johnson, T.M., Makdisi, R.S., Basu, A. (2010) Cr Stable Isotopes As Indicators of Cr(VI) Reduction in Groundwater: A Detailed Time-Series Study of a Point-Source Plume. Environmental Science & Technology 44, 1043–1048.
).The unexplained variability in εkin for Cr(VI) reduction, which ranges from -0.2 ‰ to -5 ‰, poses a barrier to interpretation of Cr isotope signatures (Qin and Wang, 2017
Qin, L., Wang, X. (2017) Chromium Isotope Geochemistry. Reviews in Mineralogy and Geochemistry 82, 379–414.
). Although faster reduction often causes less fractionation of Cr(VI) (Sikora et al., 2008Sikora, E.R., Johnson, T.M., Bullen, T.D. (2008) Microbial mass-dependent fractionation of chromium isotopes. Geochimica et Cosmochimica Acta 72, 3631–3641.
; Basu and Johnson, 2012Basu, A., Johnson, T.M. (2012) Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environmental Science & Technology 46, 5353–5360.
; Jamieson-Hanes et al., 2014Jamieson-Hanes, J.H., Lentz, A.M., Amos, R.T., Ptacek, C.J., Blowes, D.W. (2014) Examination of Cr(VI) treatment by zero-valent iron using in situ, real-time X-ray absorption spectroscopy and Cr isotope measurements. Geochimica et Cosmochimica Acta 142, 299–313.
), the origin of this effect has not been established. In accordance with predictions from electrochemical experiments, we demonstrate a log-linear relationship between εkin and k for Cr(VI) reduction by aqueous Fe(II) that arises from the dependence of both εkin and k on ΔGr°. Aqueous Fe(II) is one of the fastest naturally occurring reductants of Cr(VI) at circumneutral pH (Fendorf et al., 2000Fendorf, S., Wielinga, B.W., Hansel, C.M. (2000) Chromium Transformations in Natural Environments: The Role of Biological and Abiological Processes in Chromium(VI) Reduction. International Geology Review 42, 691–701.
), but hydrolysis and organic ligation of Fe(II) alter its standard reduction potential (E°) such that the rate constant of Cr(VI) reduction varies by orders of magnitude, depending on the speciation of Fe(II) (Buerge and Hug, 1997Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
, 1998Buerge, I.J., Hug, S.J. (1998) Influence of Organic Ligands on Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 32, 2092–2099.
). It has not been established whether changes in εkin are associated with these changes in k because fractionation during Cr(VI) reduction by aqueous Fe(II) has only been explored in a narrow pH range (Kitchen et al., 2012Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
). By changing the ligation of Fe(II), we show experimentally and theoretically that the variation in the Cr kinetic fractionation factor can be explained in terms of a linear free energy relationship.top
Results
Isotope fractionation of Cr(VI) was measured during the stepwise batch reduction of Cr(VI) by Fe(II)-citrate, Fe(II)-nitrilotriacetate, and Fe(II)-salicylate at pH 5.5 and by aqueous Fe(II) at pH values ranging from 5.0 to 7.3, following the method of Kitchen et al. (2012)
Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
. Experimental details are available in the Supplementary Information (Methods section and Table S-1). The remaining Cr(VI) was progressively enriched in heavier isotopes for all experiments. Both organic ligation of Fe(II) (Table S-2) and pH (Table S-3) affect the extent of fractionation. The observed Cr isotope fractionation can be described using a Rayleigh distillation model with a single fractionation factor (ε = α – 1, expressed in per mille) for each experiment (Figs. 1, S-1). Every experiment was carried out in duplicate, and no duplicates show major differences from each other.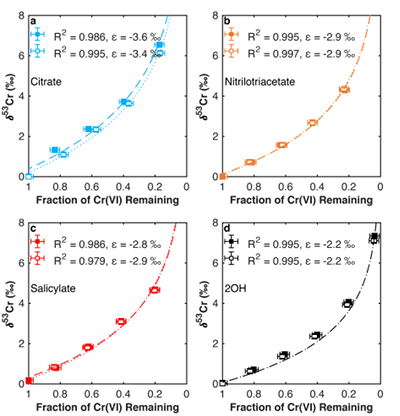
Figure 1 Isotope fractionation during Cr(VI) reduction by various aqueous Fe(II) species. Filled and open symbols in each plot show duplicate reactors. Rayleigh curves based on linear best fits are plotted as dashed lines (filled symbols) and dotted lines (open symbols). Vertical error bars (2 s.d.) are smaller than the symbols.
Jamieson-Hanes, J.H., Lentz, A.M., Amos, R.T., Ptacek, C.J., Blowes, D.W. (2014) Examination of Cr(VI) treatment by zero-valent iron using in situ, real-time X-ray absorption spectroscopy and Cr isotope measurements. Geochimica et Cosmochimica Acta 142, 299–313.
). All fractionation factors are smaller than equilibrium fractionation between inorganic Cr(VI) and Cr(III) species (-6 to -7 ‰), which is unlikely to have been approached within the experimental timescale (Schauble et al., 2004Schauble, E., Rossman, G.R., Taylor Jr., H.P. (2004) Theoretical estimates of equilibrium chromium-isotope fractionations. Chemical Geology 205, 99–114.
; Wang et al., 2015Wang, X., Johnson, T.M., Ellis, A.S. (2015) Equilibrium isotopic fractionation and isotopic exchange kinetics between Cr(III) and Cr(VI). Geochimica et Cosmochimica Acta 153, 72–90.
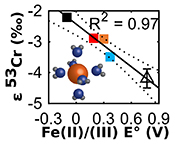
), as discussed further in the Supplementary Information. All fractionation is therefore assumed to be kinetic.Fractionation factors for Cr(VI) reduction are strongly correlated with E° of the Fe(II)-Fe(III) half -reaction, which is a proxy for ΔGr° of the electron transfers between Fe(II) and Cr(VI) (Fig. 2a). For Cr(VI) reduction by an Fe(II) species with a low E°, for which the oxidation of Fe(II) and concomitant reduction of Cr(VI) are thermodynamically favourable, the magnitude of ε is small. Furthermore, ε is also linearly correlated with log(k), whereby a faster reaction induces less fractionation (Fig. 2b). This correlation, which is consistent with previous qualitative observations (Sikora et al., 2008
Sikora, E.R., Johnson, T.M., Bullen, T.D. (2008) Microbial mass-dependent fractionation of chromium isotopes. Geochimica et Cosmochimica Acta 72, 3631–3641.
; Basu and Johnson, 2012Basu, A., Johnson, T.M. (2012) Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environmental Science & Technology 46, 5353–5360.
; Jamieson-Hanes et al., 2014Jamieson-Hanes, J.H., Lentz, A.M., Amos, R.T., Ptacek, C.J., Blowes, D.W. (2014) Examination of Cr(VI) treatment by zero-valent iron using in situ, real-time X-ray absorption spectroscopy and Cr isotope measurements. Geochimica et Cosmochimica Acta 142, 299–313.
), is unlikely to be caused by transport limitations in the vigorously stirred reactors (see Supplementary Information). Instead, the correlation between ε and log(k) is likely a by-product of the dependence of both variables on E° of the Fe(II)-Fe(III) half-reaction (Buerge and Hug, 1997Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
, 1998Buerge, I.J., Hug, S.J. (1998) Influence of Organic Ligands on Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 32, 2092–2099.
). The correlations between ε, log(k), and E° are consistent with Marcus theory and previous electrochemical observations (Kavner et al., 2005Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
, 2008Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
).
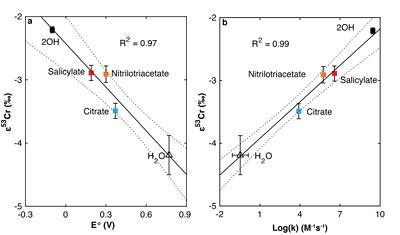
Figure 2 Linear relationships of kinetic isotope fractionation factor for Cr(VI) reduction with (a) the Fe(II)-Fe(III) standard reduction potential and (b) rate constants. Solid line shows weighted linear regression, and dotted lines show 95 % confidence interval. Each symbol shows the average fractionation factor calculated for replicate experiments. Error bars are 2 s.d. The fractionation factor for Cr(VI) reduction by Fe(H2O)62+ is taken from Kitchen et al. (2012)
Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
, and the rate constants are taken from Buerge and Hug (1997Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
, 1998Buerge, I.J., Hug, S.J. (1998) Influence of Organic Ligands on Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 32, 2092–2099.
).Jansen, B., Nierop, K.G.J., Verstraten, J.M. (2003) Mobility of Fe(II), Fe(III) and Al in acidic forest soils mediated by dissolved organic matter: influence of solution pH and metal/organic carbon ratios. Geoderma 113, 323–340.
; Morel and Price, 2003Morel, F.M.M., Price, N.M. (2003) The Biogeochemical Cycles of Trace Metals in the Oceans. Science 300, 944–947.
). Our results show that organic ligation of Fe(II) strongly affects isotope fractionation during reduction of Cr(VI) and potentially other redox partners. Similarly, fractionation during Cr(VI) reduction by aqueous inorganic Fe(II) depends on pH. Expanding the pH range of a previous study, we find that the effective fractionation factor (εeff) for Cr(VI) reduction by Fe(II) decreases in magnitude from –4.2 ‰ at pH 4.0 (Kitchen et al., 2012Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
) to -2.2 ‰ at pH 7.3 (Figs. 1, S-1; Table S-3).The pH dependence of εeff is caused by the shift in the effective reductant of Cr(VI) with pH. Three Fe(II) species reduce Cr(VI) under the reaction conditions: Fe(H2O)62+, FeOH+, and Fe(OH)20. Although the vast majority of Fe(II) is present as Fe(H2O)62+ for all tested pH values, the concentrations of the two hydrolysed species increase as pH increases. Because hydrolysis lowers E° of the Fe(II)-Fe(III) half-reaction, making Fe(II) more susceptible to oxidation, FeOH+ and Fe(OH)20 are more thermodynamically favourable and hence faster reductants of Cr(VI) (Buerge and Hug, 1997
Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
; Pettine et al., 1998Pettine, M., D’Ottone, L., Campanella, L., Millero, F.J., Passino, R. (1998) The reduction of chromium (VI) by iron (II) in aqueous solutions. Geochimica et Cosmochimica Acta 62, 1509–1519.
). Thus, as pH increases, FeOH+ and Fe(OH)20 become the dominant reductants of Cr(VI) in turn (Fig. 3a). The fraction of Cr(VI) reduced by each species in the environmentally relevant pH range of 4-7 was quantified using two species-specific rate laws from Pettine et al. (1998)Pettine, M., D’Ottone, L., Campanella, L., Millero, F.J., Passino, R. (1998) The reduction of chromium (VI) by iron (II) in aqueous solutions. Geochimica et Cosmochimica Acta 62, 1509–1519.
and Buerge and Hug (1997)Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
. Although the overall rates predicted by these models are broadly consistent, the contribution of each Fe(II) species differs.We modelled the pH dependence of εeff using the linear free energy relationship described above by conceptualising εeff as the average of the fractionation factors for Cr(VI) reduction by each Fe(II) species (i.e. Fe(H2O)62+, FeOH+, and Fe(OH)20), weighted by the fraction of Cr(VI) reduced by each species. The linear free energy relationship allows the fractionation factor for FeOH+ to be interpolated (εOH = -3.2 ‰), and interpolated fractionation factors for Fe(H2O)62+ and Fe(OH)20) are indistinguishable from the measured values. Because the two rate laws predict different contributions of each Fe(II) species to the overall reduction of Cr(VI) within the studied pH range, the models also predict different trends in εeff (Fig. 3b). Although neither model fits the data exactly, the model based on the rate law of Pettine et al. (1998)
Pettine, M., D’Ottone, L., Campanella, L., Millero, F.J., Passino, R. (1998) The reduction of chromium (VI) by iron (II) in aqueous solutions. Geochimica et Cosmochimica Acta 62, 1509–1519.
reproduces the general shape and trend of the data far better. Discrepancies are likely due to the uncertainties for the species-specific rate constants (Fig. S-2). Isotope fractionation thus offers a second axis on which to evaluate otherwise indistinguishable rate laws and improve modelling of aqueous reduction kinetics.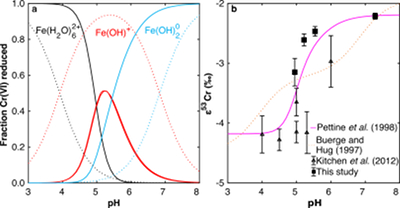
Figure 3 Effects of pH on the kinetics and isotope fractionation of Cr(VI) reduction by aqueous Fe(II). In both parts, solid lines show the model based on the rate law of Pettine et al. (1998)
Pettine, M., D’Ottone, L., Campanella, L., Millero, F.J., Passino, R. (1998) The reduction of chromium (VI) by iron (II) in aqueous solutions. Geochimica et Cosmochimica Acta 62, 1509–1519.
; dashed lines show the model based on the rate law of Buerge and Hug (1997)Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
. (a) The fraction of Cr(VI) reduced by each Fe(II) species is contingent on pH-dependent Fe(II) speciation and the rate law of Cr(VI) reduction. (b) The effective fractionation factor is the weighted average of the fractionation factors for Cr(VI) reduction by each Fe(II) species. Error bars on the symbols in (b) are 2 s.d.Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
; Basu and Johnson, 2012Basu, A., Johnson, T.M. (2012) Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environmental Science & Technology 46, 5353–5360.
; Kitchen et al., 2012Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
). Thermodynamically driven kinetic isotope effects thus explain part of the scatter in observed fractionation factors. Ultimately, predictable changes in Cr kinetic fractionation along redox gradients may help to distinguish between anoxic and euxinic palaeo-redox conditions and allow first order estimates of Cr(VI) fractionation in natural settings.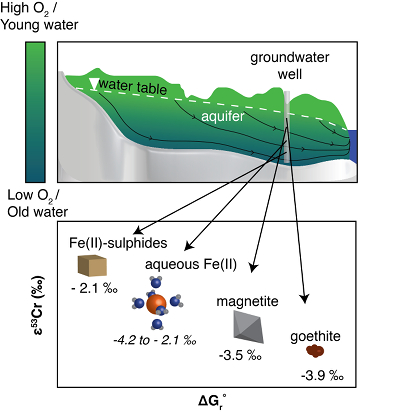
Figure 4 Schematic of Cr(VI) reduction and variations in εkin with depth, groundwater age, and oxygen levels. The dominant reductants are ordered according to their relative locations on the redox tower. Kinetic fractionation factors are taken from this study; aqueous Fe(II); Kitchen et al. (2012)
Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
, aqueous Fe(II); Basu and Johnson (2012)Basu, A., Johnson, T.M. (2012) Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environmental Science & Technology 46, 5353–5360.
, Fe(II)-doped goethite and Fe(II) sulphide, and Ellis et al. (2002)Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
, magnetite.Qin, L., Wang, X. (2017) Chromium Isotope Geochemistry. Reviews in Mineralogy and Geochemistry 82, 379–414.
), so the predicted linear free energy relationship observed herein is unambiguous. In other redox-driven systems that approach isotopic equilibrium, the relationship between observed fractionation and ΔGr° is likely more complicated. Predicting observed fractionation in these cases may require combining Marcus theory with a model that predicts the shift between kinetic and equilibrium fractionation such as that in DePaolo (2011)DePaolo, D.J. (2011) Surface kinetic model for isotopic and trace element fractionation during precipitation of calcite from aqueous solutions. Geochimica et Cosmochimica Acta 75, 1039–1056.
. Combining Marcus theory with other models would also be necessary if a significant component of fractionation is not redox-driven. Nevertheless, similar trends should exist for other redox-sensitive elements; metals such as U exhibit significant fractionation upon reduction (Brown et al., 2018Brown, S.T., Basu, A., Ding, X., Christensen, J.N., DePaolo, D.J. (2018) Uranium isotope fractionation by abiotic reductive precipitation. Proceedings of the National Academy of Sciences 201805234.
), and traditional light stable isotope systems also may be described by linear free energy relationships (Gorski et al., 2010Gorski, C.A., Nurmi, J.T., Tratnyek, P.G., Hofstetter, T.B., Scherer, M.M. (2010) Redox Behavior of Magnetite: Implications for Contaminant Reduction. Environmental Science & Technology 44, 55–60.
). By permitting more precise interpretations of redox-driven isotope fractionation, the framework presented here is poised to improve our understanding of redox dynamics.top
Acknowledgements
This work was supported by a National Science Foundation Career Award (EAR-1254156) to KM. CJ.-W was funded by the United States Department of Defense through a National Defense Science & Engineering Graduate Fellowship and by a Stanford Graduate Fellowship. STB. was funded by the U.S. Department of Energy, Office of Basic Energy Sciences (DE-AC02-05CH11231).
Editor: Liane G. Benning
top
References
Ball, J.W., Nordstrom, D.K. (1998) Critical Evaluation and Selection of Standard State Thermodynamic Properties for Chromium Metal and Its Aqueous Ions, Hydrolysis Species, Oxides, and Hydroxides. Journal of Chemical & Engineering Data 43, 895–918.
Show in context Chromium naturally occurs as Cr(VI), which is generally soluble and toxic, and as Cr(III), which is both far less soluble and environmentally benign (Ball and Nordstrom, 1998)
View in article
Basu, A., Johnson, T.M. (2012) Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environmental Science & Technology 46, 5353–5360.
Show in contextAlthough faster reduction often causes less fractionation of Cr(VI) (Sikora et al., 2008; Basu and Johnson, 2012; Jamieson-Hanes et al., 2014), the origin of this effect has not been established.
View in article
This correlation, which is consistent with previous qualitative observations (Sikora et al., 2008; Basu and Johnson, 2012; Jamieson-Hanes et al., 2014), is unlikely to be caused by transport limitations in the vigorously stirred reactors (see Supplementary Information).
View in article
We observed this quantitatively for Cr(VI) reduction by aqueous Fe(II) species (Fig. 2) and show here that the values for a more diverse set of representative reductants are broadly consistent with the predicted trend (Ellis et al., 2002; Basu and Johnson, 2012; Kitchen et al., 2012).
View in article
Figure 4 [...] Kinetic fractionation factors are taken from this study; aqueous Fe(II); Kitchen et al. (2012), aqueous Fe(II); Basu and Johnson (2012), Fe(II)-doped goethite and Fe(II) sulphide, and Ellis et al. (2002), magnetite.
View in article
Berna, E.C., Johnson, T.M., Makdisi, R.S., Basu, A. (2010) Cr Stable Isotopes As Indicators of Cr(VI) Reduction in Groundwater: A Detailed Time-Series Study of a Point-Source Plume. Environmental Science & Technology 44, 1043–1048.
Show in context In modern environments, Cr(VI) isotope signatures may fingerprint reduction of Cr(VI) pollution (Berna et al., 2010).
View in article
Brown, S.T., Basu, A., Ding, X., Christensen, J.N., DePaolo, D.J. (2018) Uranium isotope fractionation by abiotic reductive precipitation. Proceedings of the National Academy of Sciences 201805234.
Show in contextNevertheless, similar trends should exist for other redox-sensitive elements; metals such as U exhibit significant fractionation upon reduction (Brown et al., 2018), and traditional light stable isotope systems also may be described by linear free energy relationships (Gorski et al., 2010).
View in article
Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
Show in context Aqueous Fe(II) is one of the fastest naturally occurring reductants of Cr(VI) at circumneutral pH (Fendorf et al., 2000), but hydrolysis and organic ligation of Fe(II) alter its standard reduction potential (E°) such that the rate constant of Cr(VI) reduction varies by orders of magnitude, depending on the speciation of Fe(II) (Buerge and Hug, 1997, 1998).
View in article
Instead, the correlation between ε and log(k) is likely a by-product of the dependence of both variables on E° of the Fe(II)-Fe(III) half-reaction (Buerge and Hug, 1997, 1998).
View in article
Figure 2 [...] The fractionation factor for Cr(VI) reduction by Fe(H2O)62+ is taken from Kitchen et al. (2012), and the rate constants are taken from Buerge and Hug (1997, 1998).
View in article
Because hydrolysis lowers E° of the Fe(II)-Fe(III) half-reaction, making Fe(II) more susceptible to oxidation, FeOH+ and Fe(OH)20 are more thermodynamically favourable and hence faster reductants of Cr(VI) (Buerge and Hug, 1997; Pettine et al., 1998).
View in article
The fraction of Cr(VI) reduced by each species in the environmentally relevant pH range of 4-7 was quantified using two species-specific rate laws from Pettine et al. (1998) and Buerge and Hug (1997).
View in article
Figure 3 [...] In both parts, solid lines show the model based on the rate law of Pettine et al. (1998); dashed lines show the model based on the rate law of Buerge and Hug (1997)
View in article
Buerge, I.J., Hug, S.J. (1998) Influence of Organic Ligands on Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 32, 2092–2099.
Show in context Aqueous Fe(II) is one of the fastest naturally occurring reductants of Cr(VI) at circumneutral pH (Fendorf et al., 2000), but hydrolysis and organic ligation of Fe(II) alter its standard reduction potential (E°) such that the rate constant of Cr(VI) reduction varies by orders of magnitude, depending on the speciation of Fe(II) (Buerge and Hug, 1997, 1998).
View in article
Instead, the correlation between ε and log(k) is likely a by-product of the dependence of both variables on E° of the Fe(II)-Fe(III) half-reaction (Buerge and Hug, 1997, 1998).
View in article
Figure 2 [...] The fractionation factor for Cr(VI) reduction by Fe(H2O)62+ is taken from Kitchen et al. (2012), and the rate constants are taken from Buerge and Hug (1997, 1998).
View in article
Champ, D.R., Gulens, J., Jackson, R.E. (1979) Oxidation–reduction sequences in ground water flow systems. Canadian Journal of Earth Sciences 16, 12–23.
Show in contextFor example, as an oxidant such as Cr(VI) enters an aquifer and travels along a flow path characterised by decreasing O2 and Eh, Cr(VI) also encounters a changing series of abiotic reductants, e.g., from trace Fe(II) sorbed onto goethite to aqueous Fe(II) to Fe(II) sulphides, in broad accordance with the redox ladder (Champ et al., 1979).
View in article
DePaolo, D.J. (2011) Surface kinetic model for isotopic and trace element fractionation during precipitation of calcite from aqueous solutions. Geochimica et Cosmochimica Acta 75, 1039–1056.
Show in context For instance, fractionation during precipitation can be modelled as a function of solvation energies and the composition of ions in solution or the balance between forward and backward reaction rates (Fantle and DePaolo, 2007; DePaolo, 2011; Hofmann et al., 2012; Nielsen et al., 2012).
View in article
Unlike other models that link changes in observed fractionation with shifts between kinetic and equilibrium fractionation (DePaolo, 2011), Marcus theory predicts changes in the kinetic fractionation factor itself.
View in article
Predicting observed fractionation in these cases may require combining Marcus theory with a model that predicts the shift between kinetic and equilibrium fractionation such as that in DePaolo (2011).
View in article
Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
Show in context Stable isotope fractionation is used to examine Earth processes ranging from the evolution of redox conditions in ancient oceans (Frei et al., 2009) to the fate of modern contaminant plumes (Ellis et al., 2002).
View in article
Fractionation during Cr(VI) reduction induces kinetic fractionation that enriches the remaining Cr(VI) in the heavier isotopes (Ellis et al., 2002).
View in article
This fractionation may be documented as positive isotopic excursions in the rock record (Ellis et al., 2002; Frei et al., 2009).
View in article
We observed this quantitatively for Cr(VI) reduction by aqueous Fe(II) species (Fig. 2) and show here that the values for a more diverse set of representative reductants are broadly consistent with the predicted trend (Ellis et al., 2002; Basu and Johnson, 2012; Kitchen et al., 2012).
View in article
Figure 4 [...] Kinetic fractionation factors are taken from this study; aqueous Fe(II); Kitchen et al. (2012), aqueous Fe(II); Basu and Johnson (2012), Fe(II)-doped goethite and Fe(II) sulphide, and Ellis et al. (2002), magnetite.
View in article
Fantle, M.S., DePaolo, D.J. (2007) Ca isotopes in carbonate sediment and pore fluid from ODP Site 807A: The Ca2+(aq)–calcite equilibrium fractionation factor and calcite recrystallization rates in Pleistocene sediments. Geochimica et Cosmochimica Acta 71, 2524–2546.
Show in context For instance, fractionation during precipitation can be modelled as a function of solvation energies and the composition of ions in solution or the balance between forward and backward reaction rates (Fantle and DePaolo, 2007; DePaolo, 2011; Hofmann et al., 2012; Nielsen et al., 2012).
View in article
Fendorf, S., Wielinga, B.W., Hansel, C.M. (2000) Chromium Transformations in Natural Environments: The Role of Biological and Abiological Processes in Chromium(VI) Reduction. International Geology Review 42, 691–701.
Show in context Aqueous Fe(II) is one of the fastest naturally occurring reductants of Cr(VI) at circumneutral pH (Fendorf et al., 2000), but hydrolysis and organic ligation of Fe(II) alter its standard reduction potential (E°) such that the rate constant of Cr(VI) reduction varies by orders of magnitude, depending on the speciation of Fe(II) (Buerge and Hug, 1997, 1998).
View in article
Frei, R., Gaucher, C., Poulton, S.W., Canfield, D.E. (2009) Fluctuations in Precambrian atmospheric oxygenation recorded by chromium isotopes. Nature 461, 250–253.
Show in contextStable isotope fractionation is used to examine Earth processes ranging from the evolution of redox conditions in ancient oceans (Frei et al., 2009) to the fate of modern contaminant plumes (Ellis et al., 2002).
View in article
This fractionation may be documented as positive isotopic excursions in the rock record (Ellis et al., 2002; Frei et al., 2009).
View in article
Gorski, C.A., Nurmi, J.T., Tratnyek, P.G., Hofstetter, T.B., Scherer, M.M. (2010) Redox Behavior of Magnetite: Implications for Contaminant Reduction. Environmental Science & Technology 44, 55–60.
Show in context Nevertheless, similar trends should exist for other redox-sensitive elements; metals such as U exhibit significant fractionation upon reduction (Brown et al., 2018), and traditional light stable isotope systems also may be described by linear free energy relationships (Gorski et al., 2010).
View in article
Hofmann, A.E., Bourg, I.C., DePaolo, D.J. (2012) Ion desolvation as a mechanism for kinetic isotope fractionation in aqueous systems. Proceedings of the National Academy of Sciences 109, 18689–18694.
Show in context For instance, fractionation during precipitation can be modelled as a function of solvation energies and the composition of ions in solution or the balance between forward and backward reaction rates (Fantle and DePaolo, 2007; DePaolo, 2011; Hofmann et al., 2012; Nielsen et al., 2012).
View in article
Jamieson-Hanes, J.H., Lentz, A.M., Amos, R.T., Ptacek, C.J., Blowes, D.W. (2014) Examination of Cr(VI) treatment by zero-valent iron using in situ, real-time X-ray absorption spectroscopy and Cr isotope measurements. Geochimica et Cosmochimica Acta 142, 299–313.
Show in context Although faster reduction often causes less fractionation of Cr(VI) (Sikora et al., 2008; Basu and Johnson, 2012; Jamieson-Hanes et al., 2014), the origin of this effect has not been established.
View in article
The 2 ‰ range nearly spans the range of all reported fractionation factors for naturally occurring abiotic reductants of Cr(VI) (Jamieson-Hanes et al., 2014).
View in article
This correlation, which is consistent with previous qualitative observations (Sikora et al., 2008; Basu and Johnson, 2012; Jamieson-Hanes et al., 2014), is unlikely to be caused by transport limitations in the vigorously stirred reactors (see Supplementary Information).
View in article
Jansen, B., Nierop, K.G.J., Verstraten, J.M. (2003) Mobility of Fe(II), Fe(III) and Al in acidic forest soils mediated by dissolved organic matter: influence of solution pH and metal/organic carbon ratios. Geoderma 113, 323–340.
Show in context For example, organic ligation of aqueous Fe(II) is significant in marine systems and many subsurface environments (Jansen et al., 2003; Morel and Price, 2003).
View in article
Kavner, A., Bonet, F., Shahar, A., Simon, J., Young, E. (2005) The isotopic effects of electron transfer: An explanation for Fe isotope fractionation in nature. Geochimica et Cosmochimica Acta 69, 2971–2979.
Show in context Similarly, Kavner and colleagues have shown that kinetic fractionation during metal electroplating scales linearly with the standard electrode potential (E°) (Kavner et al., 2005, 2008).
View in article
Kavner and colleagues have shown that Marcus theory also describes kinetic isotope fractionation during redox reactions (Kavner et al., 2005, 2008).
View in article
The correlations between ε, log(k), and E° are consistent with Marcus theory and previous electrochemical observations (Kavner et al., 2005, 2008).
View in article
Kavner, A., John, S.G., Sass, S., Boyle, E.A. (2008) Redox-driven stable isotope fractionation in transition metals: Application to Zn electroplating. Geochimica et Cosmochimica Acta 72, 1731–1741.
Show in context Similarly, Kavner and colleagues have shown that kinetic fractionation during metal electroplating scales linearly with the standard electrode potential (E°) (Kavner et al., 2005, 2008).
View in article
Kavner and colleagues have shown that Marcus theory also describes kinetic isotope fractionation during redox reactions (Kavner et al., 2005, 2008).
View in article
The correlations between ε, log(k), and E° are consistent with Marcus theory and previous electrochemical observations (Kavner et al., 2005, 2008).
View in article
Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
Show in context It has not been established whether changes in εkin are associated with these changes in k because fractionation during Cr(VI) reduction by aqueous Fe(II) has only been explored in a narrow pH range (Kitchen et al., 2012).
View in article
Isotope fractionation of Cr(VI) was measured during the stepwise batch reduction of Cr(VI) by Fe(II)-citrate, Fe(II)-nitrilotriacetate, and Fe(II)-salicylate at pH 5.5 and by aqueous Fe(II) at pH values ranging from 5.0 to 7.3, following the method of Kitchen et al. (2012).
View in article
Figure 2 [...] The fractionation factor for Cr(VI) reduction by Fe(H2O)62+ is taken from Kitchen et al. (2012), and the rate constants are taken from Buerge and Hug (1997, 1998).
View in article
Expanding the pH range of a previous study, we find that the effective fractionation factor (εeff) for Cr(VI) reduction by Fe(II) decreases in magnitude from –4.2 ‰ at pH 4.0 (Kitchen et al., 2012) to -2.2 ‰ at pH 7.3 (Figs. 1, S-1; Table S-3).
View in article
We observed this quantitatively for Cr(VI) reduction by aqueous Fe(II) species (Fig. 2) and show here that the values for a more diverse set of representative reductants are broadly consistent with the predicted trend (Ellis et al., 2002; Basu and Johnson, 2012; Kitchen et al., 2012).
View in article
Figure 4 [...] Kinetic fractionation factors are taken from this study; aqueous Fe(II); Kitchen et al. (2012), aqueous Fe(II); Basu and Johnson (2012), Fe(II)-doped goethite and Fe(II) sulphide, and Ellis et al. (2002), magnetite.
View in article
Marcus, R.A. (1964) Chemical and electrochemical electron-transfer theory. Annual Review of Physical Chemistry 15, 155–196.
Show in context The relationship between thermodynamic parameters (E° or ΔGr°) and the kinetics of electron transfer can be formalised via Marcus theory (Marcus, 1964, 1965, 1993).
View in article
Marcus, R.A. (1965) On the Theory of Electron‐Transfer Reactions. VI. Unified Treatment for Homogeneous and Electrode Reactions. The Journal of Chemical Physics 43, 679–701.
Show in context The relationship between thermodynamic parameters (E° or ΔGr°) and the kinetics of electron transfer can be formalised via Marcus theory (Marcus, 1964, 1965, 1993).
View in article
Marcus, R.A. (1993) Electron transfer reactions in chemistry. Theory and experiment. Reviews of Modern Physics 65, 599–610.
Show in context The relationship between thermodynamic parameters (E° or ΔGr°) and the kinetics of electron transfer can be formalised via Marcus theory (Marcus, 1964, 1965, 1993).
View in article
Morel, F.M.M., Price, N.M. (2003) The Biogeochemical Cycles of Trace Metals in the Oceans. Science 300, 944–947.
Show in context For example, organic ligation of aqueous Fe(II) is significant in marine systems and many subsurface environments (Jansen et al., 2003; Morel and Price, 2003).
View in article
Nielsen, L.C., DePaolo, D.J., De Yoreo, J.J. (2012) Self-consistent ion-by-ion growth model for kinetic isotopic fractionation during calcite precipitation. Geochimica et Cosmochimica Acta 86, 166–181.
Show in contextFor instance, fractionation during precipitation can be modelled as a function of solvation energies and the composition of ions in solution or the balance between forward and backward reaction rates (Fantle and DePaolo, 2007; DePaolo, 2011; Hofmann et al., 2012; Nielsen et al., 2012).
View in article
Pettine, M., D’Ottone, L., Campanella, L., Millero, F.J., Passino, R. (1998) The reduction of chromium (VI) by iron (II) in aqueous solutions. Geochimica et Cosmochimica Acta 62, 1509–1519.
Show in contextBecause hydrolysis lowers E° of the Fe(II)-Fe(III) half-reaction, making Fe(II) more susceptible to oxidation, FeOH+ and Fe(OH)20 are more thermodynamically favourable and hence faster reductants of Cr(VI) (Buerge and Hug, 1997; Pettine et al., 1998).
View in article
The fraction of Cr(VI) reduced by each species in the environmentally relevant pH range of 4-7 was quantified using two species-specific rate laws from Pettine et al. (1998) and Buerge and Hug (1997).
View in article
Although neither model fits the data exactly, the model based on the rate law of Pettine et al. (1998) reproduces the general shape and trend of the data far better.
View in article
Figure 3 [...] In both parts, solid lines show the model based on the rate law of Pettine et al. (1998); dashed lines show the model based on the rate law of Buerge and Hug (1997)
View in article
Qin, L., Wang, X. (2017) Chromium Isotope Geochemistry. Reviews in Mineralogy and Geochemistry 82, 379–414.
Show in context The unexplained variability in εkin for Cr(VI) reduction, which ranges from -0.2 ‰ to -5 ‰, poses a barrier to interpretation of Cr isotope signatures (Qin and Wang, 2017).
View in article
Fractionation during Cr(VI) reduction is generally solely kinetic (Qin and Wang, 2017), so the predicted linear free energy relationship observed herein is unambiguous.
View in article
Schauble, E., Rossman, G.R., Taylor Jr., H.P. (2004) Theoretical estimates of equilibrium chromium-isotope fractionations. Chemical Geology 205, 99–114.
Show in context All fractionation factors are smaller than equilibrium fractionation between inorganic Cr(VI) and Cr(III) species (-6 to -7 ‰), which is unlikely to have been approached within the experimental timescale (Schauble et al., 2004; Wang et al., 2015), as discussed further in the Supplementary Information.
View in article
Sikora, E.R., Johnson, T.M., Bullen, T.D. (2008) Microbial mass-dependent fractionation of chromium isotopes. Geochimica et Cosmochimica Acta 72, 3631–3641.
Show in contextAlthough faster reduction often causes less fractionation of Cr(VI) (Sikora et al., 2008; Basu and Johnson, 2012; Jamieson-Hanes et al., 2014), the origin of this effect has not been established.
View in article
This correlation, which is consistent with previous qualitative observations (Sikora et al., 2008; Basu and Johnson, 2012; Jamieson-Hanes et al., 2014), is unlikely to be caused by transport limitations in the vigorously stirred reactors (see Supplementary Information).
View in article
Wang, X., Johnson, T.M., Ellis, A.S. (2015) Equilibrium isotopic fractionation and isotopic exchange kinetics between Cr(III) and Cr(VI). Geochimica et Cosmochimica Acta 153, 72–90.
Show in context Chromium(VI) reduction was chosen because it consistently results in kinetic isotope fractionation (Wang et al., 2015) and is actively cycled in aquifers and marine sediments, even though the multi-electron reduction is more difficult to model explicitly.
View in article
All fractionation factors are smaller than equilibrium fractionation between inorganic Cr(VI) and Cr(III) species (-6 to -7 ‰), which is unlikely to have been approached within the experimental timescale (Schauble et al., 2004; Wang et al., 2015), as discussed further in the Supplementary Information.
View in article
top
Supplementary Information
The Supplementary Information includes:
- Methods
- Kinetic Fractionation
- Tables S-1 to S-4
- Figures S-1 and S-2
- Supplementary Information References
Kitchen et al. (2012)
</a><br><br><div style=width:100%;text-align:right;> <a href=#top>top</a><br></div></div> <a name=fullimgs></a><div class=fullresolution id=fullimgs><h2>Figures and Tables</h2> <a name=Fig1-full></a><figure> <img class=edito src=http://www.geochemicalperspectivesletters.org/wp-content/uploads/2020/04/GPL1909_Fig1_790.jpg align=middle><figcaption> <br><b>Figure 1</b> Isotope fractionation during Cr(VI) reduction by various aqueous Fe(II) species. Filled and open symbols in each plot show duplicate reactors. Rayleigh curves based on linear best fits are plotted as dashed lines (filled symbols) and dotted lines (open symbols). Vertical error bars (2 s.d.) are smaller than the symbols.</figcaption><a href=../article1909#Fig1>Back to article</a> | <a href=../documents/GPL1909_Fig1.pptx>Download in Powerpoint</a></figure> <br><a name=Fig2-full></a><figure> <img class=edito src=http://www.geochemicalperspectivesletters.org/wp-content/uploads/2020/04/GPL1909_Fig2_790.jpg align=middle><figcaption> <br><b>Figure 2</b> Linear relationships of kinetic isotope fractionation factor for Cr(VI) reduction with <strong>(a) </strong>the Fe(II)-Fe(III) standard reduction potential and <strong>(b)</strong> rate constants. Solid line shows weighted linear regression, and dotted lines show 95 % confidence interval. Each symbol shows the average fractionation factor calculated for replicate experiments. Error bars are 2 s.d. The fractionation factor for Cr(VI) reduction by Fe(H<sub>2</sub>O)<sub>6</sub><sup>2+</sup> is taken from <span class=anchorBulle onclick=){kind=link}
Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
, and the rate constants are taken from Buerge and Hug (1997Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
, 1998Buerge, I.J., Hug, S.J. (1998) Influence of Organic Ligands on Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 32, 2092–2099.
).Back to article | Download in Powerpoint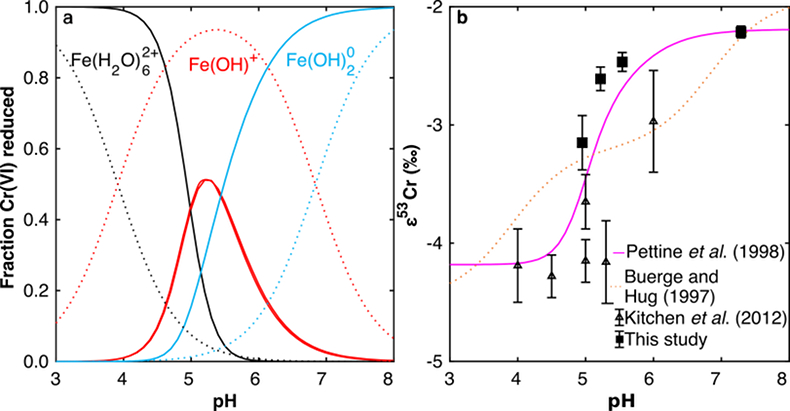
Figure 3 Effects of pH on the kinetics and isotope fractionation of Cr(VI) reduction by aqueous Fe(II). In both parts, solid lines show the model based on the rate law of Pettine et al. (1998)
Pettine, M., D’Ottone, L., Campanella, L., Millero, F.J., Passino, R. (1998) The reduction of chromium (VI) by iron (II) in aqueous solutions. Geochimica et Cosmochimica Acta 62, 1509–1519.
; dashed lines show the model based on the rate law of Buerge and Hug (1997)Buerge, I.J., Hug, S.J. (1997) Kinetics and pH Dependence of Chromium(VI) Reduction by Iron(II). Environmental Science & Technology 31, 1426–1432.
. (a) The fraction of Cr(VI) reduced by each Fe(II) species is contingent on pH-dependent Fe(II) speciation and the rate law of Cr(VI) reduction. (b) The effective fractionation factor is the weighted average of the fractionation factors for Cr(VI) reduction by each Fe(II) species. Error bars on the symbols in (b) are 2 s.d.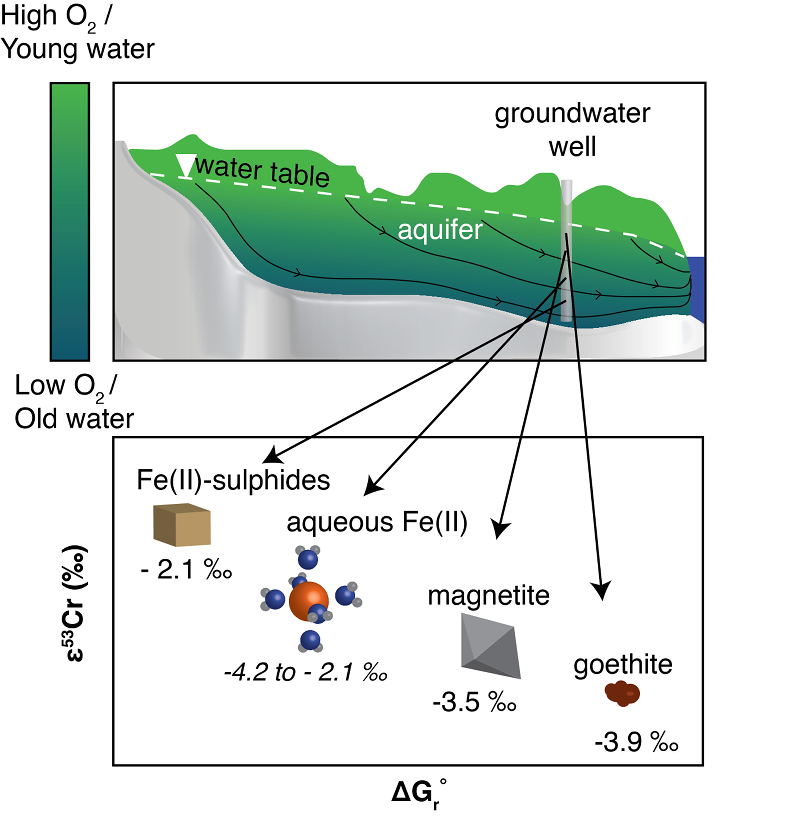
Figure 4 Schematic of Cr(VI) reduction and variations in εkin with depth, groundwater age, and oxygen levels. The dominant reductants are ordered according to their relative locations on the redox tower. Kinetic fractionation factors are taken from this study; aqueous Fe(II); Kitchen et al. (2012)
Kitchen, J.W., Johnson, T.M., Bullen, T.D., Zhu, J., Raddatz, A. (2012) Chromium isotope fractionation factors for reduction of Cr(VI) by aqueous Fe(II) and organic molecules. Geochimica et Cosmochimica Acta 89, 190–201.
, aqueous Fe(II); Basu and Johnson (2012)Basu, A., Johnson, T.M. (2012) Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environmental Science & Technology 46, 5353–5360.
, Fe(II)-doped goethite and Fe(II) sulphide, and Ellis et al. (2002)Ellis, A.S., Johnson, T.M., Bullen, T.D. (2002) Chromium Isotopes and the Fate of Hexavalent Chromium in the Environment. Science 295, 2060–2062.
, magnetite.