Triple oxygen isotopes of meteoric hydrothermal systems – implications for palaeoaltimetry
Affiliations | Corresponding Author | Cite as | Funding information- Share this article





-
Article views:555Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
. In doing so we: 1) test whether meteoric water values estimated from previous δ18O and δD analyses on quartz, feldspar and biotite are robust and 2) determine the palaeoelevation of the Eocene highlands that are presently constrained primarily by the δ18O and δD of paired muscovite and quartz from core complexes and altered granites.Our calculated δ18O values of meteoric water are higher than estimates that use combined feldspar δ18O and biotite δD measurements in these hydrothermally altered granites and δD values from muscovite from nearby core complexes (Mulch et al., 2004
Mulch, A., Teyssier, C., Cosca, M.A., Vanderhaeghe, O., Vennemann, T. (2004) Reconstructing paleoelevation in eroded orogens. Geology 32, 525–528.
). Both methods are consistent with a high elevation (∼3.1 to 4.7 km) Eocene highland in the northwestern U.S. Cordillera.Figures
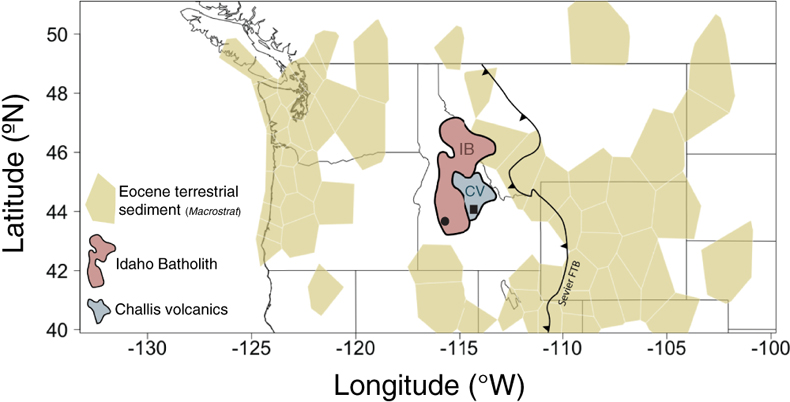
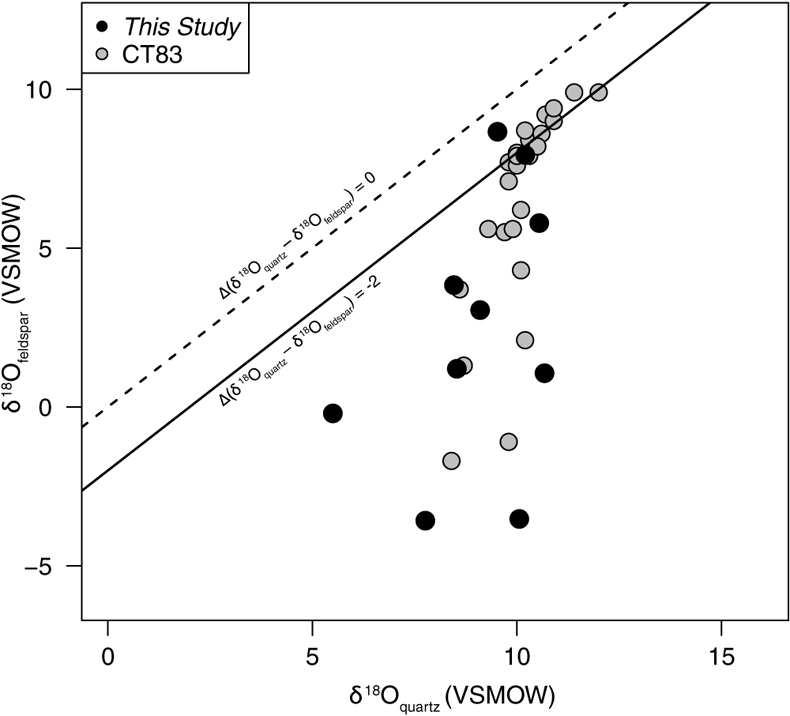
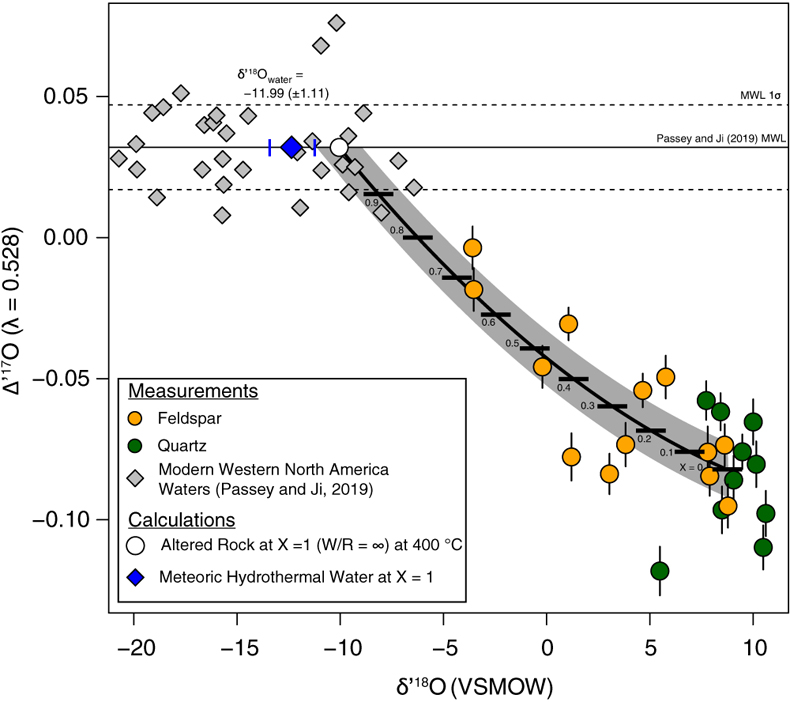
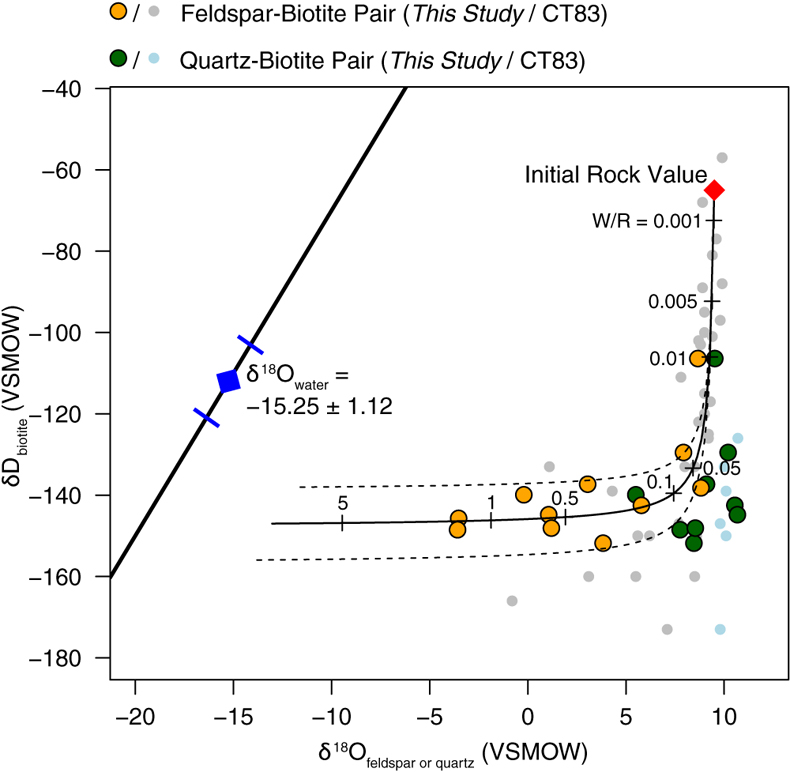
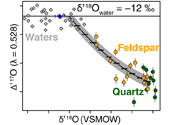
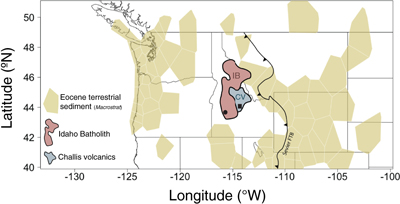 Figure 1 Map of Idaho batholith and surrounding Eocene basins. Symbols represent the study area (dot), and the Pioneer core complex (square). | 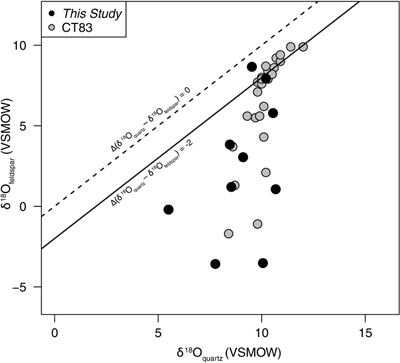 Figure 2 δ18Oquartz versus δ18Oplagioclase for coexisiting mineral pairs. Black dots are this study and gray dots those of Criss and Taylor (1983). Shown are the Δqtz-plag for 0 and 2.0 ‰. 2.0 ‰ is the equilibrium fractionation between quartz and feldpsar for granitic rocks (O’Neil and Taylor, 1967). | 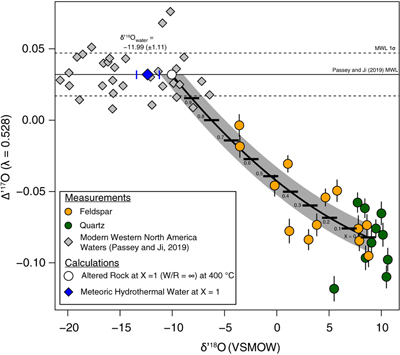 Figure 3 The δ′18O –Δ′17O alteration relationship of feldspar used to derive meteoric water. Meteoric water lines and compiled modern water data are from Passey and Ji (2019). Given are the 1 s.e. bars for the measurements. The black line is the alteration array between unaltered rock and rock in equilibrium with the metoric water fit to the feldspar data for fractional mixing (Taylor, 1978). | 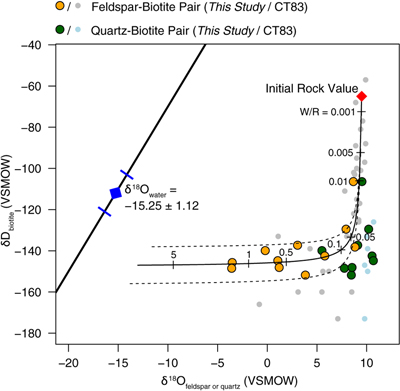 Figure 4 The δ18O–δD array for feldspar-biotite (this study; Criss and Taylor, 1983) with water/rock (W/R) values of the molar fraction of oxygen given the best fit meteoric water value. W/R values assume fractionation factors of feldspar-H2O = +2 ‰ for δ18O and biotite-H2O = −35 ‰ for δD (Taylor, 1977). Quartz values were not used for calculations. |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
top
Introduction
With the advent of stable isotope palaeoaltimetry it has been possible to determine the past elevations of the worlds major mountain belts by exploiting the relationship between δ18O and δD of meteoric waters and elevation as described by Rayleigh distillation over orography (Poage and Chamberlain, 2001
Poage, M.A., Chamberlain, C.P. (2001) Empirical relationships between elevation and the stable isotope composition of precipitation and surface waters: Considerations for studies of paleoelevation change. American Journal of Science 301, 1–15.
; Rowley et al., 2001Rowley, D.B., Pierrehumbert, R.T., Currie, B.S. (2001) A new approach to stable isotope-based paleoaltimetry: implications for paleoaltimetry and paleohypsometry of the High Himalaya since the Late Miocene. Earth and Planetary Science Letters 188, 253–268.
). Multiple proxies for the isotopic composition of meteoric waters have been used for these elevation reconstructions. These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010Hren, M.T., Pagani, M., Erwin, D.M., Brandon, M. (2010) Biomarker reconstruction of the early Eocene paleotopography and paleoclimate of the northern Sierra Nevada. Geology 38, 7–10.
), hydrated volcanic glasses (Mulch et al., 2008Mulch, A., Sarna-Wojcicki, A.M., Perkins, M.E., Chamberlain, C.P. (2008) A Miocene to Pleistocene climate and elevation record of the Sierra Nevada (California). Proceedings of the National Academy of Sciences of the United States of America 105, 6819–6824.
), pedogenic clays (Chamberlain et al., 1999Chamberlain, C.P., Poage, M., Craw, D., Reynolds, R. (1999) Topographic development of the Southern Alps recorded by the isotopic composition of authigenic clay minerals, South Island, New Zealand. Chemical Geology 155, 279–294.
), hydrothermal micas (Mulch et al., 2004Mulch, A., Teyssier, C., Cosca, M.A., Vanderhaeghe, O., Vennemann, T. (2004) Reconstructing paleoelevation in eroded orogens. Geology 32, 525–528.
), fluid inclusions of quartz veins (Sharp et al., 2005Sharp, Z.D., Masson, H., Lucchini, R. (2005) Stable isotope geochemistry and formation mechanisms of quartz veins: extreme paleoaltitudes of the central Alps in the Neogene. American Journal of Science 305, 187–219.
); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007Quade, J., Garzione, C., Eiler, J. (2007) Paleoelevation reconstruction using pedogenic carbonates. In: Kohn, M. (Ed.) Reviews in Mineralogy and Geochemistry 66, 53–87.
), lacustrine chert (Davis et al., 2009Davis, S.J., Mulch, A., Caroll, A.R., Horton, T.W., Chamberlain, C.P. (2009) Paleogene landscape evolution of the central North American Cordillera: Developing topography and hydrology in the Laramide foreland. Geological Society of America Bulletin 121, 100–116.
), and pedogenic clays (Mix and Chamberlain, 2014Mix, H.T., Chamberlain, C.P. (2014) Stable isotopic records of hydrologic change and paleotemperature from smectite in Cenozoic Western North America. Geochimica et Cosmochimica Acta 141, 532–546.
). While these proxies are excellent predictors of the isotopic composition of meteoric waters they are limited by their geographic location as many occur only in the sedimentary basins that flank the crystalline cores of mountain belts. Nowhere is this more prevalent than in the North American Cordillera where almost all palaeolevation estimates come from intermontane basins that are adjacent to crystalline uplifts (Chamberlain et al., 2012Chamberlain, C.P., Mix, H.T., Mulch, A., Hren, M.T., Kent-Corson, M.L., Davis, S.J., Horton, T.W., Graham, S.A. (2012) The Cenozoic climatic and topographic evolution of the western North American Cordillera. American Journal of Science 312, 213–262.
; Fig. 1).
Figure 1 Map of Idaho batholith and surrounding Eocene basins. Symbols represent the study area (dot), and the Pioneer core complex (square).
Most determinations of the isotopic composition of meteoric waters using crystalline rocks rely on the δD of micas from hydrothermally altered rocks within fault zones (Mulch et al., 2004
Mulch, A., Teyssier, C., Cosca, M.A., Vanderhaeghe, O., Vennemann, T. (2004) Reconstructing paleoelevation in eroded orogens. Geology 32, 525–528.
) or altered granites (Criss and Taylor, 1983Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
). A potential problem with this approach is that hydrogen isotopes of phyllosilicates may continue to exchange well after crystallisation. For example, O’Neil and Kharaka (1976)O’Neil, J.R., Kharaka, Y.K. (1976) Hydrogen and oxygen isotope exchange reactions between clay minerals and water. Geochimica et Cosmochimica Acta 40, 241–246.
showed that exchange of hydrogen, but not oxygen, occurred in clay minerals at temperatures above 100 °C. It is also possible that micas may be exchanging H rather than OH groups and that this exchange occurs at temperatures typical of cooling crystalline rocks. If this is the case, then the oxygen and hydrogen isotope values of micas may be decoupled and cooling rate dependent (Graham et al., 1987Graham, C.M., Viglino, J.A., Harmon, R.S. (1987) Experimental study of hydrogen-isotope exchange between aluminous chlorite and water and of hydrogen diffusion in chlorite. American Mineralogist 72, 566–579.
). Hence, the motivation of this study is to use triple oxygen isotopes to determine the isotopic composition of meteoric waters. Unlike the H-O system, the 17O/16O and 18O/16O systems are not decoupled, and should change in concert during alteration.To estimate the isotopic compositon of meteoric water in a hydrothermal system, we modify the approach of Herwartz et al. (2015)
Herwartz, D., Pack, A., Krylov, D., Xiao, Y., Muehlenbachs, K., Sengupta, S., Di Rocco, T. (2015) Revealing the climate of snowball Earth from Δ17O systematics of hydrothermal rocks. Proceedings of the National Academy of Sciences 112, 5337–5341.
who used arrays of triple oxygen isotopes on a suite of rocks to determine the δ18O of alteration waters during a Snowball Earth event (see also Zakharov et al., 2017Zakharov, D.O., Bindeman, I.N., Slabunov, A.I., Ovtcharova, M., Coble, M.A., Serebryakov, N.S., Schaltegger, U. (2017) Dating the Paleoproterozoic snowball Earth glaciations using contemporaneous subglacial hydrothermal systems. Geology 45, 667–670.
). Here, we use mixing equations (Taylor, 1978Taylor, H.P. Jr. (1978) Oxygen and hydrogen isotope systematics of plutonic granitic rocks. Earth and Planetary Science Letters 38, 177–210.
) modified for 17O to determine the palaeoelevation of Eocene hydrothermally altered rocks of the Idaho batholith (Criss and Taylor, 1983Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
). We show that triple oxygen isotopes correspond to Eocene meteoric water values that are higher than those determined by hydrogen isotope analysis, suggesting that retrograde hydrogen, but not oxygen, isotope exchange has occurred between micas and fluids.top
Geologic Setting
The Idaho batholith (∼25 000 km2) lies within the crystalline core of the North American Cordillera. It is flanked on both the west and east by Cenozoic intermontane basins that contain debri eroded from the batholith and surrounding rocks (Fig. 1). The batholith is Cretaceous to Eocene in age and consists of granites and granodiorites (Gaschnig et al., 2010
Gaschnig, R.M., Vervoort, J.D., Lewis, R.S., McClelland, W.C. (2010) Migrating magmatism in the northern US Cordillera: in situ U-Pb geochronology of the Idaho batholith. Contributions to Mineralogy and Petrology 159, 863–883.
). The batholith was hydrothermally altered during the emplacment of the Eocene plutons and eruption of the Challis volcanics. Using hydrogen and oxygen isotopes of minerals from these Eocene granites, Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
demonstrated that the hydrothermal systems consisted of meteoric waters within flow systems centred on the Eocene plutons. The hydrothermal centre targeted here, the Rocky Bar complex, lies in the southwest corner of the Idaho Batholith.The Rocky Bar complex was emplaced (∼48 Ma; Gaschnig et al., 2010
Gaschnig, R.M., Vervoort, J.D., Lewis, R.S., McClelland, W.C. (2010) Migrating magmatism in the northern US Cordillera: in situ U-Pb geochronology of the Idaho batholith. Contributions to Mineralogy and Petrology 159, 863–883.
) and hydrothermally altered (∼45 to 37 Ma; Criss et al., 1982Criss, R.E., Lanphere, M.A., Taylor, H.P. Jr. (1982) Effects of regional uplift, deformation and meteoric-hydrothermal metamorphism on K-Ar ages of biotites in the southern half of the Idaho Batholith. Journal of Geophysical Research 87, 7026–7046.
) during the Eocene. The alteration of the pluton and wallrocks is evidenced by low δ18O values of plagioclase (down to −2.5 ‰), with the lowest values occuring near the core of the pluton and along the faults that ring the complex. Guided by the results of Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
, we collected granites from the Rocky Bar complex exposed along Highway 21 that transects the complex (Table S-1).top
Results
Our analysis of δ18O, δ17O of plagioclase and quartz, and δD of biotite give three results, which are:
First, the δ18O of plagioclase has larger variations than that of quartz. The δ18O of plagioclase ranges from −3.6 to 8.8 ‰; quartz δ18O values range from 5.5 to 10.7 ‰ (Table S-1). Moreover, the δ18O of coexisiting mineral pairs form disequilibrium arrays (Fig. 2) similar to those discovered by Criss and Taylor (1983)
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
. Second, the Δ′17O (δ′17O –0.528 × δ′18O) of plagioclase, like the δ18O values, show a wider range than that of quartz. Δ′17O of plagioclase ranges from −0.004 to −0.095, and Δ′17O of quartz ranges from −0.058 to −0.118. Third, the δ18O of feldspar and δD values of biotite also form a water-rock mixing array (Fig. 4, Table S-1).
Figure 2 δ18Oquartz versus δ18Oplagioclase for coexisiting mineral pairs. Black dots are this study and gray dots those of Criss and Taylor (1983)
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
. Shown are the Δqtz-plag for 0 and 2.0 ‰. 2.0 ‰ is the equilibrium fractionation between quartz and feldpsar for granitic rocks (O’Neil and Taylor, 1967O’Neil, J.R., Taylor, H.P. Jr. (1967) The oxygen isotope and cation exchange chemistry of feldspars. American Mineralogist 52, 1414–1437.
).top
Interpretation
Our results agree with the interpretation that the oxygen and hydrogen isotopes reflect a high temperature hydrothermal system during emplacment of the Eocene plutons (Criss and Taylor, 1983
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
). Disequilibrium arrays of the oxygen isotopes of paired quartz and plagioclase (Fig. 2) result from differential exchange between fluids and quartz/feldspar during hydrothermal activity, with feldspar exchanging more rapidly than quartz. These kinetic controls are also reflected in the Δ′17O values.The kinetic effects are evidenced by the wide range of λquartz-feldspar values. Note that, following Pack and Herwartz (2014)
Pack, A., Herwartz, D. (2014). The triple oxygen isotope composition of the Earth mantle and understanding ΔO17 variations in terrestrial rocks and minerals. Earth and Planetary Science Letters 390, 138–145.
and Sharp et al. (2018)Sharp, Z.D., Wostbrock, J.A.G., Pack, A. (2018) Mass-dependent triple oxygen isotope variations in terrestrial materials. Geochemical Perspectives Letters 7, 27–31.
, we use θ to represent the theoretical slope, whereas λ is used to represent the empirical slope using data. As stated above our λquartz-feldspar values range from 0.5152 to 0.5305 (Table S-1). The theoretical high temperature slope is θ = 0.5305 (Young et al., 2002Young, E.D., Galy, A. Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
). Given the wide range of λquartz-feldspar values (Table S-1) and the narrow temperature range experienced by these granites and high temperature fluids it is highly unlikely that these minerals are in isotopic equilibrium. Thus, our results are consistent with the interpretation of Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
, but with the added constraint that we can calculate the meteoric water composition using oxygen isotopes alone.To determine the oxygen isotopic composition of meteoric water we used the array of δ′18O and Δ′17O (Fig. 3) values for plagioclase. A fit through this array (see Supplementary Information) using the water-rock equations of Taylor (1978)
Taylor, H.P. Jr. (1978) Oxygen and hydrogen isotope systematics of plutonic granitic rocks. Earth and Planetary Science Letters 38, 177–210.
assuming a 400 °C alteration temperature, gives a value of δ18O of meteoric water of −11.99 ‰ (±1.11, 1σ). Propagating the unceratiny around the meteoric water line of Passey and Ji (2019)Passey, B. H., Ji, H. (2019) Triple oxygen isotope signatures of evaporation in lake waters and carbonates: A case study from the western United States. Earth and Planetary Science Letters 518, 1–12.
(dashed lines in Fig. 3) and the best fit regression shown in Figure 3, produces a field spanning −10 to −15 ‰ (see Table S-2). Additionally, if the feldspar-H2O interaction is set to a colder temperature, such as 250 °C, rather than the maximum 400 °C assumed by Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
, we calculate a δ18O of meteoric water of −15 ‰ (Fig. S-1). However, this lower temperature is probably unreasonable given that it is below the closure temperature of the dated hydrothermal micas (Criss and Taylor, 1983Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
). Regardless, it is clear that the Eocene meteoric water has a low δ18O value. However, our δ18O value is higher than that determined previously (approximately −16 ‰) by Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
who use both δ18O and δD values. Our δ18O-δD data give results similar to Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
with a best fit to the data of δ18O = −15.25 ‰ (±1.12, 1σ; Fig. 4).
Figure 3 The δ′18O –Δ′17O alteration relationship of feldspar used to derive meteoric water. Meteoric water lines and compiled modern water data are from Passey and Ji (2019)
Passey, B. H., Ji, H. (2019) Triple oxygen isotope signatures of evaporation in lake waters and carbonates: A case study from the western United States. Earth and Planetary Science Letters 518, 1–12.
. Given are the 1 s.e. bars for the measurements. The black line is the alteration array between unaltered rock and rock in equilibrium with the metoric water fit to the feldspar data for fractional mixing (Taylor, 1978Taylor, H.P. Jr. (1978) Oxygen and hydrogen isotope systematics of plutonic granitic rocks. Earth and Planetary Science Letters 38, 177–210.
).
Figure 4 The δ18O–δD array for feldspar-biotite (this study; Criss and Taylor, 1983
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
) with water/rock (W/R) values of the molar fraction of oxygen given the best fit meteoric water value. W/R values assume fractionation factors of feldspar-H2O = +2 ‰ for δ18O and biotite-H2O = −35 ‰ for δD (Taylor, 1977Taylor, H.P. Jr. (1977) Water/rock interactions and the origin of H2O in granitic batholiths. Journal Geological Society of London 133, 509–558.
). Quartz values were not used for calculations.top
Discussion and Conclusions
Most estimates of the isotopic composition of meteoric waters that interacted with crystalline rocks rely on the hydrogen isotope composition of the altered rocks. The isotopic composition of these waters is either calculated directly from δD values of hydrous minerals and using temperatures from oxygen isotope thermometry (Mulch et al., 2004
Mulch, A., Teyssier, C., Cosca, M.A., Vanderhaeghe, O., Vennemann, T. (2004) Reconstructing paleoelevation in eroded orogens. Geology 32, 525–528.
) or from combined oxygen and hydrogen isotope analyses of rocks and their hydrothermally altered end members and the mixing relationships between them (Criss and Taylor, 1983Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
). Because of the possibility of exchange of hydrogen between minerals and later fluids it is a concern that estimates of the original composition of the meteoric water in these hydrothermal systems is compromised. This difference in calculated meteoric water compositons is measurable and can lead to error in estimates of the isotopic composition of meteoric waters during hydrothermal activity. The error then translates directly to error in palaeoelevation estimates, particularly at low elevations.For example, we demonstrate that based on the extrapolated mixing relationships in triple oxygen isotope space using feldspar analyses give calculated meteoric water values, assuming 400 °C, that are ∼2.7 to 3.9 ‰ (Table S-2) higher than those determined using combined oxygen and hydrogen isotopes. We note that this difference in calculated meteoric water values is dependent upon the assumed temperature of the hydrothermal system and the choice of the meteoric water lines in δ′18O and Δ′17O space (Table S-1). If we take the maximum temperature of the hydrothermal system of 400 °C (Criss and Taylor, 1983
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
) will this isotopic difference translate into an elevation difference that is significant? To test this we use the data presented here, with that published on nearby Eocene (38 to 37 Ma) Pioneer core complexes (McFadden et al., 2015McFadden, R.R., Mulch, A., Teyssier, C., Heizker, M. (2015) Extension and meteoric fluid flow in the Wildhorse detachment, Pioneer metamorphic core complex, Idaho. Lithosphere 7, 355–366.
) and the Idaho batholith (Criss and Taylor, 1983Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
) (Fig. 1). These three studies all differ in their calculation of the isotopic composition of meteoric waters. Ours is based on triple oxygen and the others rely on hydrogen isotopes. McFadden et al. (2015)McFadden, R.R., Mulch, A., Teyssier, C., Heizker, M. (2015) Extension and meteoric fluid flow in the Wildhorse detachment, Pioneer metamorphic core complex, Idaho. Lithosphere 7, 355–366.
use the δD values of micas from detachment faults active in the late Eocene and assumed temperature of formation of these detachments and calculate a δ18O of meteoric water of −16.0 ± 1.5 ‰. Criss and Taylor (1983)Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
use δD of biotites and muscovite and the δ18O of feldspar and vein quartz and arrive at the same δ18O of meteoric water of −16 ‰. Using the equations for Eocene lapse rates of Rowley et al. (2001)Rowley, D.B., Pierrehumbert, R.T., Currie, B.S. (2001) A new approach to stable isotope-based paleoaltimetry: implications for paleoaltimetry and paleohypsometry of the High Himalaya since the Late Miocene. Earth and Planetary Science Letters 188, 253–268.
, the Eocene elevation of the Idaho batholith was 4.74 km (+0.64/−0.49, 1σ of the Rowley model) based on hydrogen isotopes. Using the best fit of meteoric water at 400 °C alteration temperature (−11.92 ‰) we estimate a lower Eocene elevation of 3.11 km +0.31/−0.38 (1σ), based on triple oxygen isotopes. At 1σ and even at 2σ these values do not overlap, though they do overlap at 2σ using other meteoric water lines (Table S-2). Nonetheless, we suggest that later hydrogen exchange, at least in this case, results in inaccurate palaeoelevation estimates.top
Acknowledgements
This research was funded by NSF EAR-1322084 and Heising Simons grants to CPC. DEI was supported by Miller Research Institute and UC President’s Postdoctoral Fellowships. MKL was supported by the Agouron Institute Geobiology Fellowship. We thank Daniel Herwartz and Andreas Pack for reviews.
Editor: Eric H. Oelkers
top
References
Chamberlain, C.P., Poage, M., Craw, D., Reynolds, R. (1999) Topographic development of the Southern Alps recorded by the isotopic composition of authigenic clay minerals, South Island, New Zealand. Chemical Geology 155, 279–294.
 Show in context
Show in contextThese include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
Chamberlain, C.P., Mix, H.T., Mulch, A., Hren, M.T., Kent-Corson, M.L., Davis, S.J., Horton, T.W., Graham, S.A. (2012) The Cenozoic climatic and topographic evolution of the western North American Cordillera. American Journal of Science 312, 213–262.
 Show in context
Show in contextNowhere is this more prevalent than in the North American Cordillera where almost all palaeolevation estimates come from intermontane basins that are adjacent to crystalline uplifts (Chamberlain et al., 2012; Fig. 1).
View in article
Criss, R.R., Taylor, H.P. Jr. (1983) An 18O/16O and D/H study of Tertiary hydrothermal system in the southern half of the Idaho batholith. Geological Society of America Bulletin 94, 640–663.
 Show in context
Show in contextWe use triple oxygen isotopes of altered granitic rocks to determine the isotope composition of meteoric waters in a fossil hydrothermal system, the low δ18O Eocene Idaho Batholith, originally studied by Criss and Taylor (1983).
View in article
Most determinations of the isotopic composition of meteoric waters using crystalline rocks rely on the δD of micas from hydrothermally altered rocks within fault zones (Mulch et al., 2004) or altered granites (Criss and Taylor, 1983).
View in article
Here, we use mixing equations (Taylor, 1978) modified for 17O to determine the palaeoelevation of Eocene hydrothermally altered rocks of the Idaho batholith (Criss and Taylor, 1983).
View in article
Using hydrogen and oxygen isotopes of minerals from these Eocene granites, Criss and Taylor (1983) demonstrated that the hydrothermal systems consisted of meteoric waters within flow systems centred on the Eocene plutons
View in article
Guided by the results of Criss and Taylor (1983), we collected granites from the Rocky Bar complex exposed along Highway 21 that transects the complex (Table S-1)
View in article
Moreover, the δ18O of coexisiting mineral pairs form disequilibrium arrays (Fig. 2) similar to those discovered by Criss and Taylor (1983).
View in article
Black dots are this study and gray dots those of Criss and Taylor (1983).
View in article
Our results agree with the interpretation that the oxygen and hydrogen isotopes reflect a high temperature hydrothermal system during emplacment of the Eocene plutons (Criss and Taylor, 1983).
View in article
Thus, our results are consistent with the interpretation of Criss and Taylor (1983), but with the added constraint that we can calculate the meteoric water composition using oxygen isotopes alone.
View in article
Additionally, if the feldspar-H2O interaction is set to a colder temperature, such as 250 °C, rather than the maximum 400 °C assumed by Criss and Taylor (1983), we calculate a δ18O of meteoric water of −15 ‰ (Fig. S-1).
View in article
However, this lower temperature is probably unreasonable given that it is below the closure temperature of the dated hydrothermal micas (Criss and Taylor, 1983).
View in article
However, our δ18O value is higher than that determined previously (approximately −16 ‰) by Criss and Taylor (1983) who use both δ18O and δD values.
View in article
Our δ18O-δD data give results similar to Criss and Taylor (1983) with a best fit to the data of δ18O = −15.25 ‰ (±1.12, 1σ;
View in article
The δ18O–δD array for feldspar-biotite (this study; Criss and Taylor, 1983) with water/rock (W/R) values of the molar fraction of oxygen given the best fit meteoric water value.
View in article
The isotopic composition of these waters is either calculated directly from δD values of hydrous minerals and using temperatures from oxygen isotope thermometry (Mulch et al., 2004) or from combined oxygen and hydrogen isotope analyses of rocks and their hydrothermally altered end members and the mixing relationships between them (Criss and Taylor, 1983).
View in article
If we take the maximum temperature of the hydrothermal system of 400 °C (Criss and Taylor, 1983) will this isotopic difference translate into an elevation difference that is significant?
View in article
To test this we use the data presented here, with that published on nearby Eocene (38 to 37 Ma) Pioneer core complexes (McFadden et al., 2015) and the Idaho batholith (Criss and Taylor, 1983) (
View in article
Criss, R.E., Lanphere, M.A., Taylor, H.P. Jr. (1982) Effects of regional uplift, deformation and meteoric-hydrothermal metamorphism on K-Ar ages of biotites in the southern half of the Idaho Batholith. Journal of Geophysical Research 87, 7026–7046.
 Show in context
Show in context The Rocky Bar complex was emplaced (∼48 Ma; Gaschnig et al., 2010) and hydrothermally altered (∼45 to 37 Ma; Criss et al., 1982) during the Eocene.
View in article
Davis, S.J., Mulch, A., Caroll, A.R., Horton, T.W., Chamberlain, C.P. (2009) Paleogene landscape evolution of the central North American Cordillera: Developing topography and hydrology in the Laramide foreland. Geological Society of America Bulletin 121, 100–116.
 Show in context
Show in context These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
Gaschnig, R.M., Vervoort, J.D., Lewis, R.S., McClelland, W.C. (2010) Migrating magmatism in the northern US Cordillera: in situ U-Pb geochronology of the Idaho batholith. Contributions to Mineralogy and Petrology 159, 863–883.
 Show in context
Show in context The batholith is Cretaceous to Eocene in age and consists of granites and granodiorites (Gaschnig et al., 2010).
View in article
The Rocky Bar complex was emplaced (∼48 Ma; Gaschnig et al., 2010) and hydrothermally altered (∼45 to 37 Ma; Criss et al., 1982) during the Eocene.
View in article
Graham, C.M., Viglino, J.A., Harmon, R.S. (1987) Experimental study of hydrogen-isotope exchange between aluminous chlorite and water and of hydrogen diffusion in chlorite. American Mineralogist 72, 566–579.
 Show in context
Show in context If this is the case, then the oxygen and hydrogen isotope values of micas may be decoupled and cooling rate dependent (Graham et al., 1987).
View in article
Herwartz, D., Pack, A., Krylov, D., Xiao, Y., Muehlenbachs, K., Sengupta, S., Di Rocco, T. (2015) Revealing the climate of snowball Earth from Δ17O systematics of hydrothermal rocks. Proceedings of the National Academy of Sciences 112, 5337–5341.
 Show in context
Show in context To estimate the isotopic compositon of meteoric water in a hydrothermal system, we modify the approach of Herwartz et al. (2015) who used arrays of triple oxygen isotopes on a suite of rocks to determine the δ18O of alteration waters during a Snowball Earth event (see also Zakharov et al., 2017).
View in article
Hren, M.T., Pagani, M., Erwin, D.M., Brandon, M. (2010) Biomarker reconstruction of the early Eocene paleotopography and paleoclimate of the northern Sierra Nevada. Geology 38, 7–10.
 Show in context
Show in context These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
McFadden, R.R., Mulch, A., Teyssier, C., Heizker, M. (2015) Extension and meteoric fluid flow in the Wildhorse detachment, Pioneer metamorphic core complex, Idaho. Lithosphere 7, 355–366.
 Show in context
Show in context To test this we use the data presented here, with that published on nearby Eocene (38 to 37 Ma) Pioneer core complexes (McFadden et al., 2015) and the Idaho batholith (Criss and Taylor, 1983) (
View in article
McFadden et al. (2015) use the δD values of micas from detachment faults active in the late Eocene and assumed temperature of formation of these detachments and calculate a δ18O of meteoric water of −16.0 ± 1.5 ‰.
View in article
Mix, H.T., Chamberlain, C.P. (2014) Stable isotopic records of hydrologic change and paleotemperature from smectite in Cenozoic Western North America. Geochimica et Cosmochimica Acta 141, 532–546.
 Show in context
Show in context These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
Mulch, A., Teyssier, C., Cosca, M.A., Vanderhaeghe, O., Vennemann, T. (2004) Reconstructing paleoelevation in eroded orogens. Geology 32, 525–528.
 Show in context
Show in context Our calculated δ18O values of meteoric water are higher than estimates that use combined feldspar δ18O and biotite δD measurements in these hydrothermally altered granites and δD values from muscovite from nearby core complexes (
View in article
These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
Most determinations of the isotopic composition of meteoric waters using crystalline rocks rely on the δD of micas from hydrothermally altered rocks within fault zones (Mulch et al., 2004) or altered granites (Criss and Taylor, 1983).
View in article
Mulch, A., Sarna-Wojcicki, A.M., Perkins, M.E., Chamberlain, C.P. (2008) A Miocene to Pleistocene climate and elevation record of the Sierra Nevada (California). Proceedings of the National Academy of Sciences of the United States of America 105, 6819–6824.
 Show in context
Show in context These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
O’Neil, J.R., Taylor, H.P. Jr. (1967) The oxygen isotope and cation exchange chemistry of feldspars. American Mineralogist 52, 1414–1437.
 Show in context
Show in context 2.0 ‰ is the equilibrium fractionation between quartz and feldpsar for granitic rocks (O’Neil and Taylor, 1967).
View in article
O’Neil, J.R., Kharaka, Y.K. (1976) Hydrogen and oxygen isotope exchange reactions between clay minerals and water. Geochimica et Cosmochimica Acta 40, 241–246.
 Show in context
Show in context A potential problem with this approach is that hydrogen isotopes of phyllosilicates may continue to exchange well after crystallisation. For example, O’Neil and Kharaka (1976) showed that exchange of hydrogen, but not oxygen, occurred in clay minerals at temperatures above 100 °C.
View in article
Pack, A., Herwartz, D. (2014). The triple oxygen isotope composition of the Earth mantle and understanding ΔO17 variations in terrestrial rocks and minerals. Earth and Planetary Science Letters 390, 138–145.
 Show in context
Show in context Note that, following Pack and Herwartz (2014) and Sharp et al. (2018), we use θ to represent the theoretical slope, whereas λ is used to represent the empirical slope using data.
View in article
Passey, B. H., Ji, H. (2019) Triple oxygen isotope signatures of evaporation in lake waters and carbonates: A case study from the western United States. Earth and Planetary Science Letters 518, 1–12.
 Show in context
Show in context Propagating the unceratiny around the meteoric water line of Passey and Ji (2019) (dashed lines in
View in article
Meteoric water lines and compiled modern water data are from Passey and Ji (2019).
View in article
Poage, M.A., Chamberlain, C.P. (2001) Empirical relationships between elevation and the stable isotope composition of precipitation and surface waters: Considerations for studies of paleoelevation change. American Journal of Science 301, 1–15.
 Show in context
Show in context With the advent of stable isotope palaeoaltimetry it has been possible to determine the past elevations of the worlds major mountain belts by exploiting the relationship between δ18O and δD of meteoric waters and elevation as described by Rayleigh distillation over orography (Poage and Chamberlain, 2001; Rowley et al., 2001).
View in article
Quade, J., Garzione, C., Eiler, J. (2007) Paleoelevation reconstruction using pedogenic carbonates. In: Kohn, M. (Ed.) Reviews in Mineralogy and Geochemistry 66, 53–87.
 Show in context
Show in context These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
Rowley, D.B., Pierrehumbert, R.T., Currie, B.S. (2001) A new approach to stable isotope-based paleoaltimetry: implications for paleoaltimetry and paleohypsometry of the High Himalaya since the Late Miocene. Earth and Planetary Science Letters 188, 253–268.
 Show in context
Show in context With the advent of stable isotope palaeoaltimetry it has been possible to determine the past elevations of the worlds major mountain belts by exploiting the relationship between δ18O and δD of meteoric waters and elevation as described by Rayleigh distillation over orography (Poage and Chamberlain, 2001; Rowley et al., 2001).
View in article
Using the equations for Eocene lapse rates of Rowley et al. (2001), the Eocene elevation of the Idaho batholith was 4.74 km (+0.64/−0.49, 1σ of the Rowley model) based on hydrogen isotopes.
View in article
Sharp, Z.D., Masson, H., Lucchini, R. (2005) Stable isotope geochemistry and formation mechanisms of quartz veins: extreme paleoaltitudes of the central Alps in the Neogene. American Journal of Science 305, 187–219.
 Show in context
Show in context These include the δD of 1) organic molecules from fossilised leafs (Hren et al., 2010), hydrated volcanic glasses (Mulch et al., 2008), pedogenic clays (Chamberlain et al., 1999), hydrothermal micas (Mulch et al., 2004), fluid inclusions of quartz veins (Sharp et al., 2005); and the δ18O of 2) pedogenic and lacustrine carbonate (Quade et al., 2007), lacustrine chert (Davis et al., 2009), and pedogenic clays (Mix and Chamberlain, 2014).
View in article
Sharp, Z.D., Wostbrock, J.A.G., Pack, A. (2018) Mass-dependent triple oxygen isotope variations in terrestrial materials. Geochemical Perspectives Letters 7, 27–31.
 Show in context
Show in context Note that, following Pack and Herwartz (2014) and Sharp et al. (2018), we use θ to represent the theoretical slope, whereas λ is used to represent the empirical slope using data.
View in article
Taylor, H.P. Jr. (1977) Water/rock interactions and the origin of H2O in granitic batholiths. Journal Geological Society of London 133, 509–558.
 Show in context
Show in context W/R values assume fractionation factors of feldspar-H2O = +2 ‰ for δ18O and biotite-H2O = −35 ‰ for δD (Taylor, 1977).
View in article
Taylor, H.P. Jr. (1978) Oxygen and hydrogen isotope systematics of plutonic granitic rocks. Earth and Planetary Science Letters 38, 177–210.
 Show in context
Show in context Here, we use mixing equations (Taylor, 1978) modified for 17O to determine the palaeoelevation of Eocene hydrothermally altered rocks of the Idaho batholith (Criss and Taylor, 1983).
View in article
A fit through this array (see Supplementary Information) using the water-rock equations of Taylor (1978) assuming a 400 °C alteration temperature, gives a value of δ18O of meteoric water of −11.99 ‰ (±1.11, 1σ).
View in article
The black line is the alteration array between unaltered rock and rock in equilibrium with the metoric water fit to the feldspar data for fractional mixing (Taylor, 1978).
View in article
Young, E.D., Galy, A. Nagahara, H. (2002) Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochimica et Cosmochimica Acta 66, 1095–1104.
 Show in context
Show in context The theoretical high temperature slope is θ = 0.5305 (Young et al., 2002).
View in article
Zakharov, D.O., Bindeman, I.N., Slabunov, A.I., Ovtcharova, M., Coble, M.A., Serebryakov, N.S., Schaltegger, U. (2017) Dating the Paleoproterozoic snowball Earth glaciations using contemporaneous subglacial hydrothermal systems. Geology 45, 667–670.
 Show in context
Show in context To estimate the isotopic compositon of meteoric water in a hydrothermal system, we modify the approach of Herwartz et al. (2015) who used arrays of triple oxygen isotopes on a suite of rocks to determine the δ18O of alteration waters during a Snowball Earth event (see also Zakharov et al., 2017).
View in article
top
Supplementary Information
The Supplementary Information includes:
- Supplementary Methods
- Supplementary Equations
- Tables S-1 and S-2
- Figure S-1
- Supplementary Information References
Download the Supplementary Information (PDF).
Figures