A genetic classification of the tholeiitic and calc-alkaline magma series
Affiliations | Corresponding Author | Cite as | Funding information- Share this article





-
Article views:1,372Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Figures
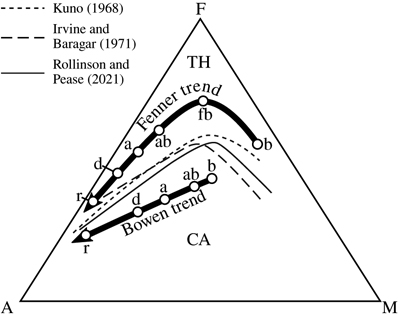 Figure 1 A–F–M diagram with three decision boundaries between the tholeiitic (TH, following the Fenner trend) and calc-alkaline (CA, following the Bowen trend) igneous suites. b = basalt, fb = ferro-basalt, ab = andesite-basalt, a = andesite, d = dacite and r = rhyolite. | 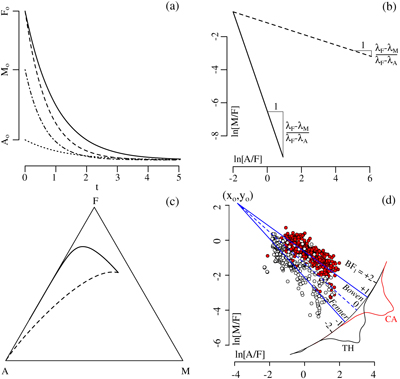 Figure 2 Exponential decay processes of compositional data become linear trends in log ratio space. (a) Temporal evolution of a magma according to Equation 2, with decay constants λF = 0.5 (solid line), λF = 0.7 (dashed line), λM = 0.8 (dash-dot line) and λA = 0.4 (dotted line), (b) removing the time dimension by plotting ln(M/F) against ln(A/F) produces two compositional trends (Eq. 4) for λF = 0.5 (solid line) and λF = 0.7 (dashed line), (c) mapping these trends to the ternary diagram yields two curved trajectories that resemble the Fenner and Bowen trends of Figure 1, (d) model fit to igneous rock compositions from Iceland (white) and the Cascade Mountains (red). Projecting the individual rock compositions onto a radial scale gives rise to the Bowen-Fenner (BF1) Index, which is shown as kernel density estimates (KDEs) for the tholeiitic (TH, black) and calc-alkaline (CA, red) samples, respectively. | 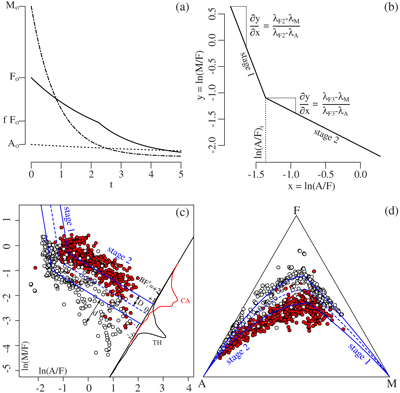 Figure 3 (a) The temporal evolution of a two stage magma evolution model (Eq. 7) for F (solid line), A (dotted line) and M (dashed-dotted line), (b) a log ratio plot of the two stage model reproduces the characteristic dog-leg in the tholeiitic magma evolution trend (Eq. 8), (c) two stage model fit to the data of Figure 2d. Solid blue lines mark the best fit of Equation 11. Dashed blue lines mark the decision boundary of Equation 12. d and D are the two distances that are needed to compute the | 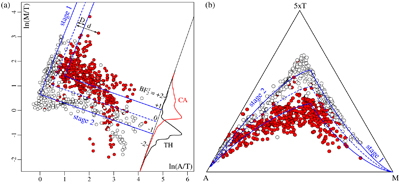 Figure 4 The two stage magma evolution model of Figure 3 and Equation 8, fitted to the A–T–M data compilation (where T = TiO2) of Rollinson and Pease (2021), shown (a) in log ratio space and (b) transformed back to the ternary diagram. Solid blue lines mark the best fit of Equation 14. Dashed blue lines mark the decision boundary of Equation 15. The frequency distributions of these |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
top
Introduction
Much petrological nomenclature predates plate tectonic theory. Without an overarching theoretical paradigm to understand petrogenesis, early 20th century geologists relied on empirical trends to classify rocks. But despite this lack of theoretical understanding, several of these empirical models survived the plate tectonic revolution and fitted neatly into a plate tectonic context.
A case in point is the division of sub-alkaline igneous rocks into tholeiitic and calc-alkaline suites. This classification has its roots in the 1920’s (Bowen, 1928
Bowen, N.L. (1928) The Evolution of the Igneous Rocks. Princeton University Press, Princeton.
; Fenner, 1929Fenner, C.N. (1929) The crystallization of basalts. American Journal of Science 105, 225–253.
; Kennedy, 1933Kennedy, W.Q. (1933) Trends of differentiation in basaltic magmas. American Journal of Science 147, 239–256.
; Tilley, 1950Tilley, C. (1950) Some aspects of magmatic evolution. Quarterly Journal of the Geological Society 106, 37–61.
) and is based on the empirical observation that, when plotting igneous rocks on an A–F–M diagram (where A = Na2O + K2O, F = FeOT, M = MgO, and A + F + M = 1), magmatic differentiation can produce a ‘Fenner trend’ (the F/M ratio increases with increasing A) or a ‘Bowen trend’ (the F/M ratio remains more constant). The Fenner and Bowen trends characterise the tholeiitic and calc-alkaline suites, respectively.The difference between tholeiitic and calc-alkaline magma sources is quite evidently related to their oxygen fugacity (Osborn, 1959
Osborn, E.F. (1959) Role of oxygen pressure in the crystallization and differentiation of basaltic magma. American Journal of Science 257, 609–647.
). In reduced magmas, Fe is removed slowly by crystallisation of Mg-rich ferrous minerals such as olivine and pyroxene. This results in an increase of the Fe/Mg ratio during the initial stages of magma evolution, producing the tholeiitic suite of rocks. Oxidising conditions in a parent magma promote the crystallisation of ferric iron-bearing magnetite, which removes Fe more efficiently, producing the calc-alkaline trend.The division of igneous rocks into tholeiitic and calc-alkaline suites makes sense in a plate tectonic context. Tholeiitic rocks are found at mid-ocean ridges, where decompression melting of the upper mantle produces primitive magmas without crustal contamination. Calc-alkaline rocks are found at subduction zones, where dehydration of the down going slab interacts with the mantle wedge and the overriding plate, resulting in a mixing of different magma sources, thus providing ample opportunity for the introduction of oxidised chemical species into the system (Kelley and Cottrell, 2009
Kelley, K.A., Cottrell, E. (2009) Water and the oxidation state of subduction zone magmas. Science 325, 605–607.
).The historical distinction between the tholeiitic and calc-alkaline magma series is descriptive, with the boundary between the two fields inferred by eye and multiple boundaries in use today (e.g., Kuno, 1968
Kuno, H. (1968) Differentiation of basalt magmas. In: Hess, H.H., Poldervaart, A. (Eds.) Basalts: The Poldervaart treatise on rocks of basaltic composition. Interscience Publishers, New York, 623–688.
; Irvine and Baragar, 1971Irvine, T.N., Baragar, W. (1971) A guide to the chemical classification of the common volcanic rocks. Canadian Journal of Earth Sciences 8, 523–548.
; Rollinson and Pease, 2021Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
). This has naturally resulted in efforts i) to disambiguate chemical descriptors from genetic implications, e.g., the high, medium, and low Fe suites of Arculus (2003)Arculus, R.J. (2003) Use and abuse of the terms calcalkaline and calcalkalic. Journal of Petrology 44, 929–935.
or MgO vs. FeO* in the modified approach of Pearce and Robinson (2010)Pearce, J.A., Robinson, P. (2010) The Troodos ophiolitic complex probably formed in a subduction initiation, slab edge setting. Gondwana Research 18, 60–81.
, and ii) to quantify the affinity of these magma series for understanding their petrogenetic evolution (the Tholeiitic Index of Zimmer et al., 2010Zimmer, M.M., Plank, T., Hauri, E.H., Yogodzinski, G.M., Stelling, P., Larsen, J., Singer, B., Jicha, B., Mandeville, C., Nye, C.J. (2010) The role of water in generating the calc-alkaline trend: new volatile data for Aleutian magmas and a new tholeiitic index. Journal of Petrology 51, 2411–2444.
). However, this work is predominantly based on mafic to intermediate compositions associated with modern volcanic systems; even Irvine and Baragar (1971)Irvine, T.N., Baragar, W. (1971) A guide to the chemical classification of the common volcanic rocks. Canadian Journal of Earth Sciences 8, 523–548.
noted the difficulty of distinguishing between the felsic compositions of the tholeiitic and calc-alkaline series on the A–F–M diagram, a result of the dominance of alkalis (Na2O + K2O) associated with the more siliceous compositions in triangular space.We use a simple theoretical model to reproduce the Fenner and Bowen trends, thereby providing a mathematical basis for the differentiation between tholeiitic and calc-alkaline rocks regardless of composition. We apply this model to TiO2 and find an acceptable alternative for discriminating between tholeiitic and calc-alkaline rocks using an A–T–M diagram. Our new classifications offer two significant advantages over the previous decision boundaries. First, they go beyond simple binary decisions and quantify the extent to which an igneous rock belongs to either suite. Second, they clarify the distinction between the two series at the dacitic–rhyolitic end of the magma series, where the Fenner and Bowen trends converge on the ternary diagram (Fig. 1).

Figure 1 A–F–M diagram with three decision boundaries between the tholeiitic (TH, following the Fenner trend) and calc-alkaline (CA, following the Bowen trend) igneous suites. b = basalt, fb = ferro-basalt, ab = andesite-basalt, a = andesite, d = dacite and r = rhyolite.
top
Log Ratio Processes in Igneous Petrology
Consider a magma containing A mass units of Na2O + K2O, F mass units of FeOT, and M mass units of MgO. Suppose that, as the magma cools, it loses components A, F and M at rates that are proportional to the amounts of A, F and M present in the magma:
Eq. 1
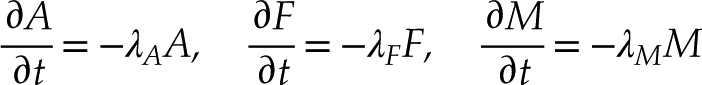
where t is time (or, more generally, differentiation progress) and
 is a decay constant (for
is a decay constant (for  ). The same mathematical formulation can be used to describe the settlement of sediment from a suspension (Egozcue et al., 2003
). The same mathematical formulation can be used to describe the settlement of sediment from a suspension (Egozcue et al., 2003Egozcue, J., Pawlowsky-Glahn, V., Mateu-Figueras, G., Barcelo-Vidal, C. (2003) Isometric Logratio Transformations for Compositional Data Analysis. Mathematical Geology 35, 279–300.
), or the decay of radioactive isotopes (Rutherford and Soddy, 1902Rutherford, E., Soddy, F. (1902) The cause and nature of radioactivity – Part I. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 21, 370–396.
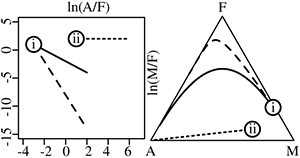
). The solution to Equation 1 is a set of exponential functions:Eq. 2
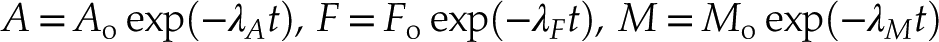
where Ao, Fo and Mo are the initial values of A, F and M in the primitive magma (Fig. 2a). Different values of
 ,
,  and
and  give rise to different trajectories on the A–F–M diagram. Combining the three compositional variables A, F and M into two log ratio variables ln(A/F) and ln(M/F) recasts the exponential functions of Equation 2 into two linear functions:
give rise to different trajectories on the A–F–M diagram. Combining the three compositional variables A, F and M into two log ratio variables ln(A/F) and ln(M/F) recasts the exponential functions of Equation 2 into two linear functions: Eq. 3
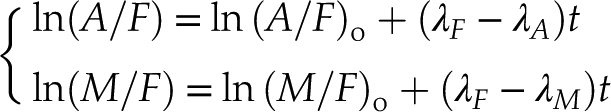
which can be combined as follows:
Eq. 4
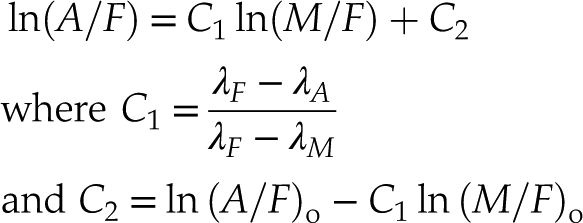
Thus, the curved trajectories on the AFM diagram become straight lines in log ratio space and vice versa (Fig. 2b,c). With an appropriate choice of initial ratios and decay constants, it is possible to mimic the Fenner and Bowen trends of the tholeiitic and calc-alkaline magma series, respectively. This makes geological sense because it is not hard to imagine how
 could depend on the oxygen fugacity in the magma, which controls the valence state of the Fe ions and, hence, the minerals that they form.
could depend on the oxygen fugacity in the magma, which controls the valence state of the Fe ions and, hence, the minerals that they form.
Figure 2 Exponential decay processes of compositional data become linear trends in log ratio space. (a) Temporal evolution of a magma according to Equation 2, with decay constants λF = 0.5 (solid line), λF = 0.7 (dashed line), λM = 0.8 (dash-dot line) and λA = 0.4 (dotted line), (b) removing the time dimension by plotting ln(M/F) against ln(A/F) produces two compositional trends (Eq. 4) for λF = 0.5 (solid line) and λF = 0.7 (dashed line), (c) mapping these trends to the ternary diagram yields two curved trajectories that resemble the Fenner and Bowen trends of Figure 1, (d) model fit to igneous rock compositions from Iceland (white) and the Cascade Mountains (red). Projecting the individual rock compositions onto a radial scale gives rise to the Bowen-Fenner (BF1) Index, which is shown as kernel density estimates (KDEs) for the tholeiitic (TH, black) and calc-alkaline (CA, red) samples, respectively.
top
Application to Iceland and the Cascades
We use the empirical data set of Rollinson and Pease (2021)
Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
as the basis for our new model. This data set includes 456 tholeiitic rocks from Iceland and 580 calc-alkaline rocks from the Cascade Mountains (see Supplementary Information for details). Plotting these compositions on a diagram of ln(M/F) vs. ln(A/F) yields two approximately linear arrays of data points, as predicted by Equation 4. Orthogonal regression of these data produces the following trends:Eq. 5
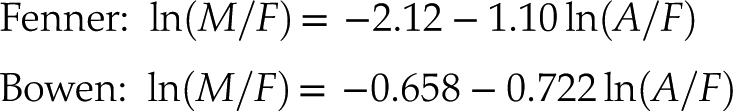
These two lines intersect at (xo = −3.84, yo = 2.12), which is equivalent to a hypothetical common magma source with a normalised A–F–M composition of (Ao = 0.23 %, Fo = 10.72 %, Mo = 89.05 %; see Fig. 2d). This fanning arrangement of linear trends provides an opportunity to quantify the degree to which a volcanic rock belongs to the tholeiitic or the calc-alkaline series. Defining the ‘single stage Bowen–Fenner (BF1) Index’ as:
Eq. 6
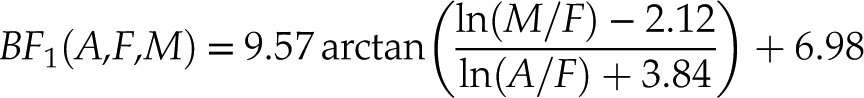
projects A–F–M compositions onto a radial scale (Fig. 2d), in which the regression line through the Iceland data is marked by a BF1 Index of −1, and the regression line through the Cascades data is marked by a BF1 Index of +1. Thus, tholeiitic and calc-alkaline rocks correspond to negative and positive BF1 values, respectively.
top
A Two Stage Magma Evolution Model
The fanning arrangement of linear trends shown in Figure 2d successfully discriminates between the calc-alkaline and tholeiitic magma series. However, it is not accurate in detail, as it fails to capture the prominent dog-leg in the tholeiitic data cloud, which reflects the transition from ferrous to ferric mineral dominated iron sequestration. Whilst Equation 5 stipulates that the tholeiitic magma series follows a single linear trend with a different slope than the calc-alkaline trend, in reality it consists of two linear segments. The first of these segments has a steeper slope than the calc-alkaline magma series. It describes the early stages of tholeiitic magma evolution, during which ferrous Fe is sequestered by minerals such as olivine and pyroxene. The second segment has the same slope as the calc-alkaline trend and describes the later stages of tholeiitic magma evolution, in which ferric Fe is sequestered by magnetite crystallisation.
This additional complexity can be captured by modifying the log ratio model of Equations 1–4 to form a two stage magma evolution history. Let
 and
and  be the magmatic decay constant of iron during the first (ferrous) and second (ferric) stage of magma fractionation, respectively, and let f mark the turning point between the first and second stage, where 0 < f < 1:
be the magmatic decay constant of iron during the first (ferrous) and second (ferric) stage of magma fractionation, respectively, and let f mark the turning point between the first and second stage, where 0 < f < 1: Eq. 7
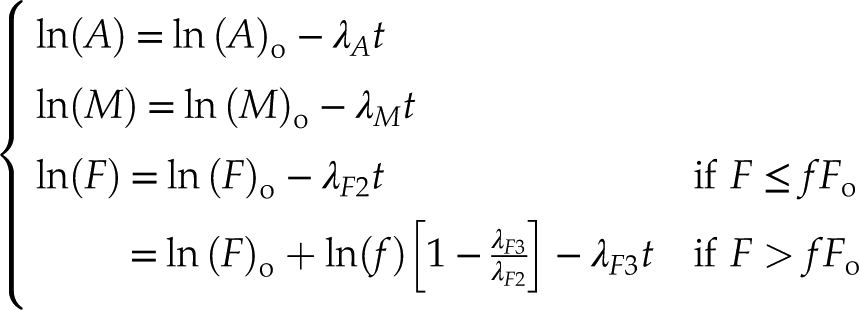
then it can be shown that:
Eq. 8
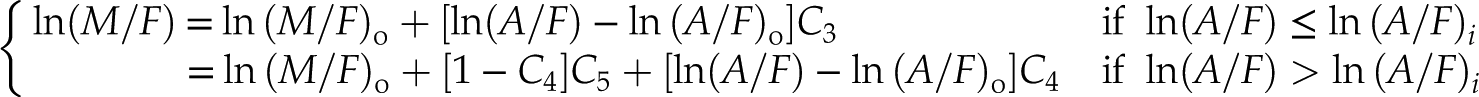
where
Eq. 9
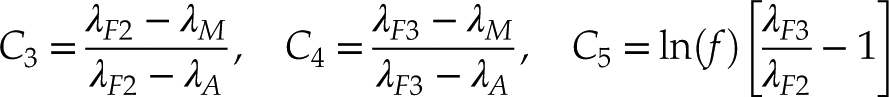
and
Eq. 10

Equation 7 describes the temporal evolution of the two stage model, which features an inflection point when the FeOT content drops to
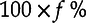 of its initial concentration Fo (Fig. 3a). In Equation 8, this inflection point occurs at the intersection of two linear trends, whose horizontal coordinate is denoted as ln(A/F)i (Fig. 3b). When
of its initial concentration Fo (Fig. 3a). In Equation 8, this inflection point occurs at the intersection of two linear trends, whose horizontal coordinate is denoted as ln(A/F)i (Fig. 3b). When  , the log ratio pattern reproduces the distinct dog-leg of the tholeiitic magma series (Fig. 3b,c).
, the log ratio pattern reproduces the distinct dog-leg of the tholeiitic magma series (Fig. 3b,c).
Figure 3 (a) The temporal evolution of a two stage magma evolution model (Eq. 7) for F (solid line), A (dotted line) and M (dashed-dotted line), (b) a log ratio plot of the two stage model reproduces the characteristic dog-leg in the tholeiitic magma evolution trend (Eq. 8), (c) two stage model fit to the data of Figure 2d. Solid blue lines mark the best fit of Equation 11. Dashed blue lines mark the decision boundary of Equation 12. d and D are the two distances that are needed to compute the
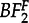 Index of each sample using Equation 13. Kernel density estimates of the
Index of each sample using Equation 13. Kernel density estimates of the 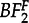 values for the Cascade and Iceland data are shown as red and black curves, respectively, (d) the two stage model fit transformed back to the ternary diagram.
values for the Cascade and Iceland data are shown as red and black curves, respectively, (d) the two stage model fit transformed back to the ternary diagram.The lower FeOT decay constant for the first stage of the magma evolution model (
 ) indicates that the rate at which iron is withdrawn from the magma is limited by the relatively low Fe content of ferrous iron-bearing minerals such as olivine and pyroxene. Once the magma transitions from a reduced to a more oxidised state, magnetite starts growing and the (ferric) iron is extracted from the magma at a higher rate, resulting in the shallower angle on the log ratio diagram. The calc-alkaline data are dominated by the second stage, which is parallel to the second stage of the tholeiitic series. However there is also a faint hint of a dog-leg in the early stages of the calc-alkaline compositions. We can therefore fit the two stage model to the calc-alkaline data as well. Joint optimisation of Equation 8 using the full Rollinson and Pease (2021)
) indicates that the rate at which iron is withdrawn from the magma is limited by the relatively low Fe content of ferrous iron-bearing minerals such as olivine and pyroxene. Once the magma transitions from a reduced to a more oxidised state, magnetite starts growing and the (ferric) iron is extracted from the magma at a higher rate, resulting in the shallower angle on the log ratio diagram. The calc-alkaline data are dominated by the second stage, which is parallel to the second stage of the tholeiitic series. However there is also a faint hint of a dog-leg in the early stages of the calc-alkaline compositions. We can therefore fit the two stage model to the calc-alkaline data as well. Joint optimisation of Equation 8 using the full Rollinson and Pease (2021)Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
data set yields the following results:Eq. 11
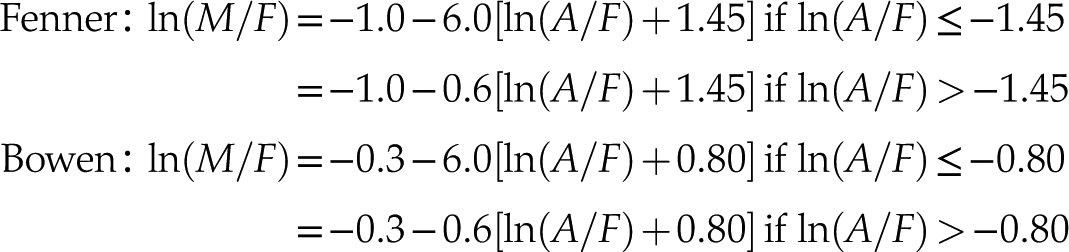
where, for the sake of parsimony, the two magma evolution trends are exactly parallel to each other. The decision boundary between the tholeiitic and calc-alkaline magma series can be defined as the halfway line between these trends:
Eq. 12
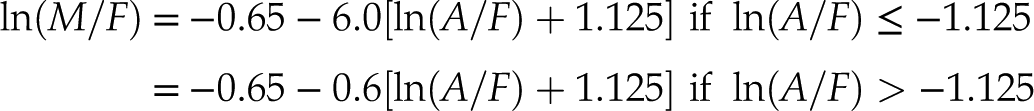
Equations 11 and 12 are shown on Figure 3c,d as solid and dashed blue lines, respectively. We can then define the ‘two stage Bowen-Fenner Index’ (
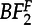 ) as
) as Eq. 13
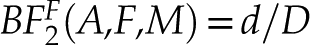
where d is the signed log ratio distance from the sample to the line defined by Equation 12, and D is half the distance between the Fenner and Bowen trends of Equation 11, measured along the projection line through the sample composition (Fig. 3c).
top
Application to Other Oxides
The Ti budget of igneous rocks is controlled by Fe–Ti oxides such as ilmenite (FeTiO3). It is therefore reasonable to expect a strong link between the temporal evolution of Fe and Ti in igneous suites. Indeed, when plotting the Rollinson and Pease (2021)
Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
data set on an A–T–M diagram (where T = TiO2 and A + T + M = 1), this separates the calc-alkaline and tholeiitic suites just as well as the A–F–M diagram does. In log ratio space, the dog-leg of the tholeiitic rocks is even more prominent than for the A–F–M data, and is also more noticeable for the calc-alkaline rocks. Fitting the two stage magma evolution model to the A–T–M data yields the following results:Eq. 14

with the decision boundary again being halfway between these two lines:
Eq. 15
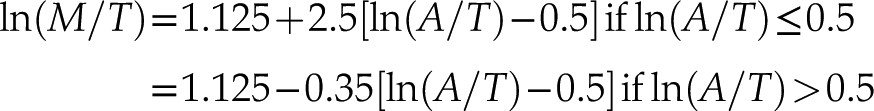
The two linear trends that constitute Equations 14 and 15 intersect at an acute angle (Fig. 4a), as opposed to the obtuse angle of Figure 3b,c. This reflects the fact that
 for the first stage and
for the first stage and  for the second stage. In contrast,
for the second stage. In contrast,  in both stages of the A–F–M model (Fig. 3a). Equations 14 and 15 can be used to define a two stage Bowen-Fenner Index (
in both stages of the A–F–M model (Fig. 3a). Equations 14 and 15 can be used to define a two stage Bowen-Fenner Index (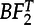 ) in complete analogy with the
) in complete analogy with the 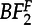 Index of Equation 13. It is also possible to combine the two indices together to form an average ‘two stage Bowen-Fenner Index’:
Index of Equation 13. It is also possible to combine the two indices together to form an average ‘two stage Bowen-Fenner Index’: Eq. 16
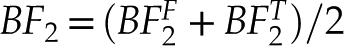

Figure 4 The two stage magma evolution model of Figure 3 and Equation 8, fitted to the A–T–M data compilation (where T = TiO2) of Rollinson and Pease (2021)
Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
, shown (a) in log ratio space and (b) transformed back to the ternary diagram. Solid blue lines mark the best fit of Equation 14. Dashed blue lines mark the decision boundary of Equation 15. The frequency distributions of these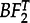 values are shown as red and black kernel density estimates for the Cascade and Iceland data, respectively.
values are shown as red and black kernel density estimates for the Cascade and Iceland data, respectively.This definition effectively extends the discrimination between the calc-alkaline and tholeiitic magma series from a three component ternary diagram to a four component compositional tetrahedron.
top
Discussion
Our method is particularly advantageous because it i) correctly deals with the statistics associated with closed data sets, ii) is quantitative, iii) provides better segregation between the two series, and iv) can be applied to plutonic rocks as well as volcanic rocks. The log ratio models enhance the ability to resolve the difference between the dacitic and rhyolitic end members of the two igneous suites, where the Fenner and Bowen trends converge with increasing alkali content. These trends are well separated in log ratio space, making it easier to distinguish compositions rich in alkali metals and leading to a more robust boundary in triangular space.
As George Box famously said, all models are wrong (but some are useful) and the simple log ratio models presented in this paper are no exception. The single stage model is clearly wrong because it fails to capture the distinct dog-leg in the tholeiitic magma series. However despite this shortcoming, the model effectively discriminates between the calc-alkaline and tholeiitic magma series. It also serves as a building block for the more realistic two stage model, which more accurately describes the geological mechanism behind the calc-alkaline and tholeiitic magma series. However, whilst more accurate than the single stage model, the two stage model is inevitably also wrong in its detail. The clean separation into two distinct sets of magmatic decay constants is an oversimplification. In reality, the transition between the ferrous and ferric stages is likely to be gradual, not abrupt.
Although we have formulated our model as a simple function of oxygen fugacity (via the parameter f in Eqs. 7 and 10), in reality there are other effects at play. This is particularly true for the later stages of continental arc magma evolution where crust-magma interactions can include melts stratified by density, magma mixing, crustal assimilation, melt stagnation at the base of the crust or in the volcano-plutonic plumbing system, etc. (see discussion in Hora et al., 2009
Hora, J.M., Singer, B.S., Wörner, G., Beard, B.L., Jicha, B.R., Johnson, C.M. (2009) Shallow and deep crustal control on differentiation of calc-alkaline and tholeiitic magma. Earth and Planetary Science Letters 285, 75–86.
). It would be easy to further improve the fit by adding further parameters, however this would reduce the numerical stability and geological interpretability of the model.Despite the simplicity of the two stage model, whose decision boundaries are completely described by just four numbers, it is highly successful in discriminating between the calc-alkaline and tholeiitic magma trends. Importantly, the same model also describes the evolution of TiO2, leading to a new A–T–M discrimination diagram. This success indicates that the exponential decay functions of Equations 1 and 2 correctly describe the temporal evolution of silicate melts. It validates the predictive power of genetic (as opposed to purely empirical) descriptions of magma evolution. The log ratio methodology provides opportunities to investigate other mineral systems, allowing igneous petrologists to move beyond descriptive geochemistry towards quantitative models that can be tested in a laboratory setting.
All the methods presented in this paper have been implemented in R and can be accessed from https://github.com/pvermees/GeoplotR/.
top
Acknowledgements
We would like to thank Julian Pearce and an anonymous reviewer for their useful comments, which led to the development of the two stage model and the addition of the A–T–M diagram to the paper. This research was supported by NERC standard grant #NE/T001518/1 and Swedish Research Council grant 2018-04372.
Editor: Horst R. Marschall
top
References
Arculus, R.J. (2003) Use and abuse of the terms calcalkaline and calcalkalic. Journal of Petrology 44, 929–935.
 Show in context
Show in context This has naturally resulted in efforts i) to disambiguate chemical descriptors from genetic implications, e.g., the high, medium, and low Fe suites of Arculus (2003) or MgO vs. FeO* in the modified approach of Pearce and Robinson (2010), and ii) to quantify the affinity of these magma series for understanding their petrogenetic evolution (the Tholeiitic Index of Zimmer et al., 2010).
View in article
Bowen, N.L. (1928) The Evolution of the Igneous Rocks. Princeton University Press, Princeton.
 Show in context
Show in context A case in point is the division of sub-alkaline igneous rocks into tholeiitic and calc-alkaline suites. This classification has its roots in the 1920’s (Bowen, 1928; Fenner, 1929; Kennedy, 1933; Tilley, 1950) and is based on the empirical observation that, when plotting igneous rocks on an A–F–M diagram (where A = Na2O + K2O, F = FeOT, M = MgO, and A + F + M = 1), magmatic differentiation can produce a ‘Fenner trend’ (the F/M ratio increases with increasing A) or a ‘Bowen trend’ (the F/M ratio remains more constant).
View in article
Egozcue, J., Pawlowsky-Glahn, V., Mateu-Figueras, G., Barcelo-Vidal, C. (2003) Isometric Logratio Transformations for Compositional Data Analysis. Mathematical Geology 35, 279–300.
 Show in context
Show in context The same mathematical formulation can be used to describe the settlement of sediment from a suspension (Egozcue et al., 2003), or the decay of radioactive isotopes (Rutherford and Soddy, 1902).
View in article
Fenner, C.N. (1929) The crystallization of basalts. American Journal of Science 105, 225–253.
 Show in context
Show in context A case in point is the division of sub-alkaline igneous rocks into tholeiitic and calc-alkaline suites. This classification has its roots in the 1920’s (Bowen, 1928; Fenner, 1929; Kennedy, 1933; Tilley, 1950) and is based on the empirical observation that, when plotting igneous rocks on an A–F–M diagram (where A = Na2O + K2O, F = FeOT, M = MgO, and A + F + M = 1), magmatic differentiation can produce a ‘Fenner trend’ (the F/M ratio increases with increasing A) or a ‘Bowen trend’ (the F/M ratio remains more constant).
View in article
Hora, J.M., Singer, B.S., Wörner, G., Beard, B.L., Jicha, B.R., Johnson, C.M. (2009) Shallow and deep crustal control on differentiation of calc-alkaline and tholeiitic magma. Earth and Planetary Science Letters 285, 75–86.
 Show in context
Show in context This is particularly true for the later stages of continental arc magma evolution where crust-magma interactions can include melts stratified by density, magma mixing, crustal assimilation, melt stagnation at the base of the crust or in the volcano-plutonic plumbing system, etc. (see discussion in Hora et al., 2009).
View in article
Irvine, T.N., Baragar, W. (1971) A guide to the chemical classification of the common volcanic rocks. Canadian Journal of Earth Sciences 8, 523–548.
 Show in context
Show in context However, this work is predominantly based on mafic to intermediate compositions associated with modern volcanic systems; even Irvine and Baragar (1971) noted the difficulty of distinguishing between the felsic compositions of the tholeiitic and calc-alkaline series on the A–F–M diagram, a result of the dominance of alkalis (Na2O + K2O) associated with the more siliceous compositions in triangular space.
View in article
The historical distinction between the tholeiitic and calc-alkaline magma series is descriptive, with the boundary between the two fields inferred by eye and multiple boundaries in use today (e.g., Kuno, 1968; Irvine and Baragar, 1971; Rollinson and Pease, 2021).
View in article
Kelley, K.A., Cottrell, E. (2009) Water and the oxidation state of subduction zone magmas. Science 325, 605–607.
 Show in context
Show in context Calc-alkaline rocks are found at subduction zones, where dehydration of the down going slab interacts with the mantle wedge and the overriding plate, resulting in a mixing of different magma sources, thus providing ample opportunity for the introduction of oxidised chemical species into the system (Kelley and Cottrell, 2009).
View in article
Kennedy, W.Q. (1933) Trends of differentiation in basaltic magmas. American Journal of Science 147, 239–256.
 Show in context
Show in context A case in point is the division of sub-alkaline igneous rocks into tholeiitic and calc-alkaline suites. This classification has its roots in the 1920’s (Bowen, 1928; Fenner, 1929; Kennedy, 1933; Tilley, 1950) and is based on the empirical observation that, when plotting igneous rocks on an A–F–M diagram (where A = Na2O + K2O, F = FeOT, M = MgO, and A + F + M = 1), magmatic differentiation can produce a ‘Fenner trend’ (the F/M ratio increases with increasing A) or a ‘Bowen trend’ (the F/M ratio remains more constant).
View in article
Kuno, H. (1968) Differentiation of basalt magmas. In: Hess, H.H., Poldervaart, A. (Eds.) Basalts: The Poldervaart treatise on rocks of basaltic composition. Interscience Publishers, New York, 623–688.
 Show in context
Show in context The historical distinction between the tholeiitic and calc-alkaline magma series is descriptive, with the boundary between the two fields inferred by eye and multiple boundaries in use today (e.g., Kuno, 1968; Irvine and Baragar, 1971; Rollinson and Pease, 2021).
View in article
Osborn, E.F. (1959) Role of oxygen pressure in the crystallization and differentiation of basaltic magma. American Journal of Science 257, 609–647.
 Show in context
Show in context The difference between tholeiitic and calc-alkaline magma sources is quite evidently related to their oxygen fugacity (Osborn, 1959).
View in article
Pearce, J.A., Robinson, P. (2010) The Troodos ophiolitic complex probably formed in a subduction initiation, slab edge setting. Gondwana Research 18, 60–81.
 Show in context
Show in context This has naturally resulted in efforts i) to disambiguate chemical descriptors from genetic implications, e.g., the high, medium, and low Fe suites of Arculus (2003) or MgO vs. FeO* in the modified approach of Pearce and Robinson (2010), and ii) to quantify the affinity of these magma series for understanding their petrogenetic evolution (the Tholeiitic Index of Zimmer et al., 2010).
View in article
Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
 Show in context
Show in context We use the empirical data set of Rollinson and Pease (2021) as the basis for our new model.
View in article
The two stage magma evolution model of Figure 3 and Equation 8, fitted to the A–T–M data compilation (where T = TiO2) of Rollinson and Pease (2021), shown (a) in log ratio space and (b) transformed back to the ternary diagram.
View in article
The historical distinction between the tholeiitic and calc-alkaline magma series is descriptive, with the boundary between the two fields inferred by eye and multiple boundaries in use today (e.g., Kuno, 1968; Irvine and Baragar, 1971; Rollinson and Pease, 2021).
View in article
Rutherford, E., Soddy, F. (1902) The cause and nature of radioactivity – Part I. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 21, 370–396.
 Show in context
Show in context The same mathematical formulation can be used to describe the settlement of sediment from a suspension (Egozcue et al., 2003), or the decay of radioactive isotopes (Rutherford and Soddy, 1902).
View in article
Tilley, C. (1950) Some aspects of magmatic evolution. Quarterly Journal of the Geological Society 106, 37–61.
 Show in context
Show in context A case in point is the division of sub-alkaline igneous rocks into tholeiitic and calc-alkaline suites. This classification has its roots in the 1920’s (Bowen, 1928; Fenner, 1929; Kennedy, 1933; Tilley, 1950) and is based on the empirical observation that, when plotting igneous rocks on an A–F–M diagram (where A = Na2O + K2O, F = FeOT, M = MgO, and A + F + M = 1), magmatic differentiation can produce a ‘Fenner trend’ (the F/M ratio increases with increasing A) or a ‘Bowen trend’ (the F/M ratio remains more constant).
View in article
Zimmer, M.M., Plank, T., Hauri, E.H., Yogodzinski, G.M., Stelling, P., Larsen, J., Singer, B., Jicha, B., Mandeville, C., Nye, C.J. (2010) The role of water in generating the calc-alkaline trend: new volatile data for Aleutian magmas and a new tholeiitic index. Journal of Petrology 51, 2411–2444.
 Show in context
Show in context This has naturally resulted in efforts i) to disambiguate chemical descriptors from genetic implications, e.g., the high, medium, and low Fe suites of Arculus (2003) or MgO vs. FeO* in the modified approach of Pearce and Robinson (2010), and ii) to quantify the affinity of these magma series for understanding their petrogenetic evolution (the Tholeiitic Index of Zimmer et al., 2010).
View in article
top
Supplementary Information
The Supplementary Information includes:
- Supplementary Text
- Supplementary Information References
Download the Supplementary Information (PDF).
Figures
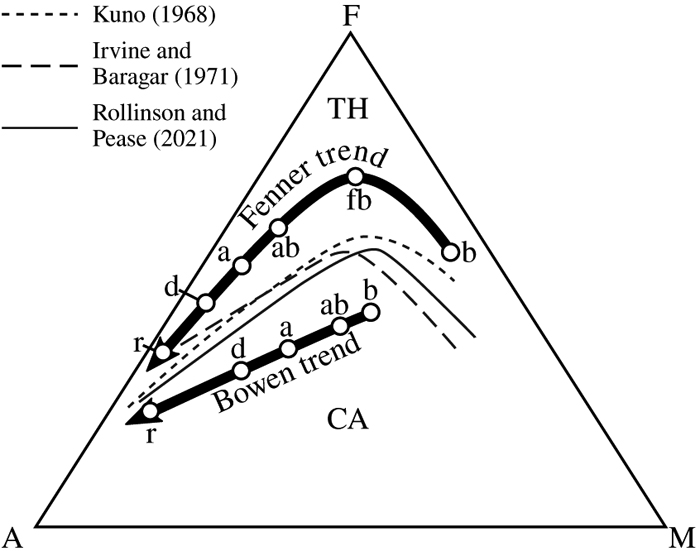
Figure 1 A–F–M diagram with three decision boundaries between the tholeiitic (TH, following the Fenner trend) and calc-alkaline (CA, following the Bowen trend) igneous suites. b = basalt, fb = ferro-basalt, ab = andesite-basalt, a = andesite, d = dacite and r = rhyolite.
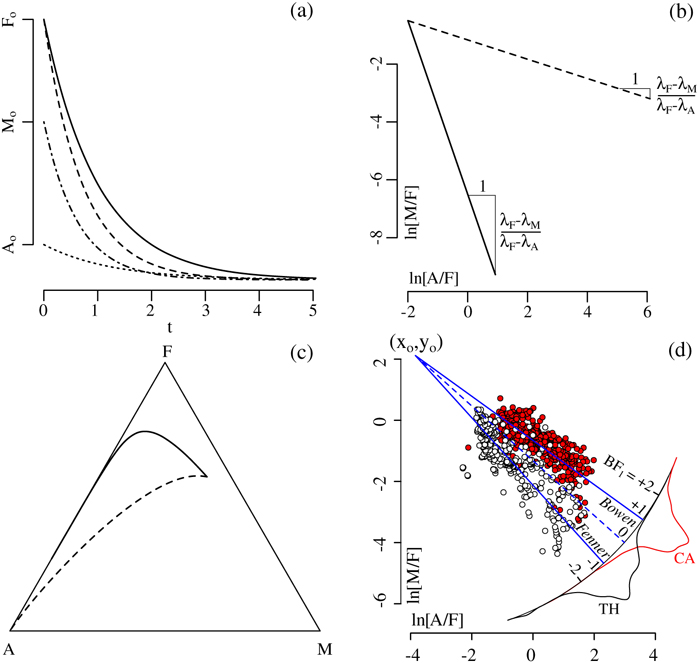
Figure 2 Exponential decay processes of compositional data become linear trends in log ratio space. (a) Temporal evolution of a magma according to Equation 2, with decay constants λF = 0.5 (solid line), λF = 0.7 (dashed line), λM = 0.8 (dash-dot line) and λA = 0.4 (dotted line), (b) removing the time dimension by plotting ln(M/F) against ln(A/F) produces two compositional trends (Eq. 4) for λF = 0.5 (solid line) and λF = 0.7 (dashed line), (c) mapping these trends to the ternary diagram yields two curved trajectories that resemble the Fenner and Bowen trends of Figure 1, (d) model fit to igneous rock compositions from Iceland (white) and the Cascade Mountains (red). Projecting the individual rock compositions onto a radial scale gives rise to the Bowen-Fenner (BF1) Index, which is shown as kernel density estimates (KDEs) for the tholeiitic (TH, black) and calc-alkaline (CA, red) samples, respectively.
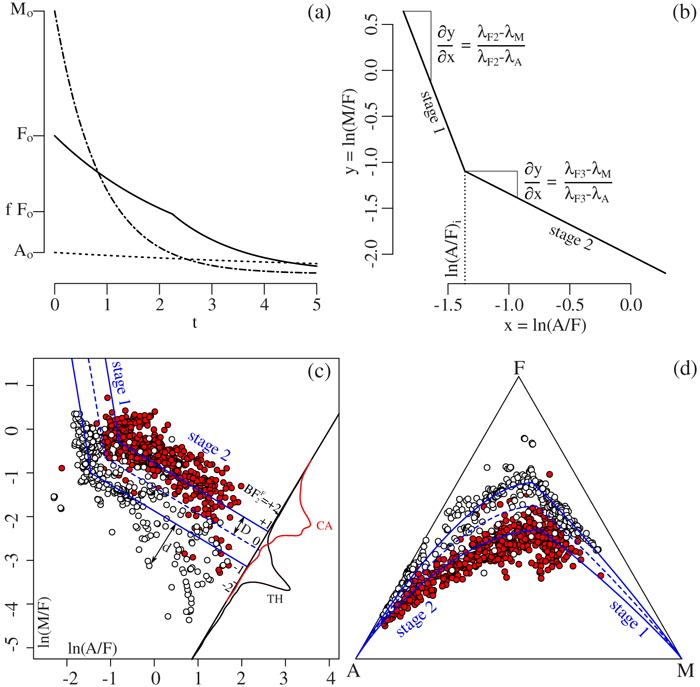
Figure 3 (a) The temporal evolution of a two stage magma evolution model (Eq. 7) for F (solid line), A (dotted line) and M (dashed-dotted line), (b) a log ratio plot of the two stage model reproduces the characteristic dog-leg in the tholeiitic magma evolution trend (Eq. 8), (c) two stage model fit to the data of Figure 2d. Solid blue lines mark the best fit of Equation 11. Dashed blue lines mark the decision boundary of Equation 12. d and D are the two distances that are needed to compute the
 Index of each sample using Equation 13. Kernel density estimates of the
Index of each sample using Equation 13. Kernel density estimates of the 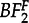 values for the Cascade and Iceland data are shown as red and black curves, respectively, (d) the two stage model fit transformed back to the ternary diagram.
values for the Cascade and Iceland data are shown as red and black curves, respectively, (d) the two stage model fit transformed back to the ternary diagram.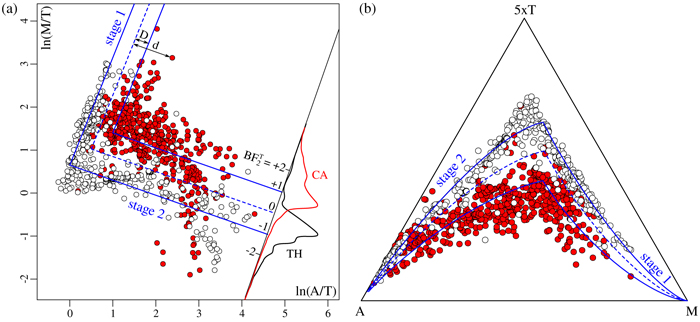
Figure 4 The two stage magma evolution model of Figure 3 and Equation 8, fitted to the A–T–M data compilation (where T = TiO2) of Rollinson and Pease (2021)
Rollinson, H., Pease, V. (2021) Using Geochemical Data to Understand Geological Processes. Second Edition, Cambridge University Press, Cambridge.
, shown (a) in log ratio space and (b) transformed back to the ternary diagram. Solid blue lines mark the best fit of Equation 14. Dashed blue lines mark the decision boundary of Equation 15. The frequency distributions of these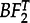 values are shown as red and black kernel density estimates for the Cascade and Iceland data, respectively.
values are shown as red and black kernel density estimates for the Cascade and Iceland data, respectively.