Zircon growth experiments reveal limited equilibrium Zr isotope fractionation in magmas
Affiliations | Corresponding Author | Cite as | Funding information- Share this article




-
Article views:408Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Figures
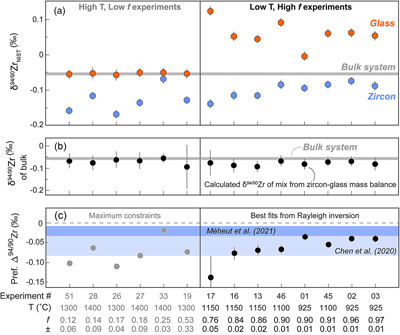 Figure 1 (a) δ94/90Zr of the glass (orange) and bulk zircon (blue) for each experiment. ‘Bulk system’ is the mean value of all experimental base mixes. (b) Mass balance calculations for all glass-zircon pairs compared to the δ94/90Zr of the bulk starting mix. (c) Apparent Δ94/90Zr, the fractionation factor between zircon and melt, determined for each experiment (see text for further details and discussion). Range of ab initio values between 1300 °C and 700 °C (Chen et al., 2020; Méheut et al., 2021) are shown as horizontal blue bands. Samples are shown rank ordered by increasing mean f. Uncertainties, visible only when larger than the symbols, are 2σ. | 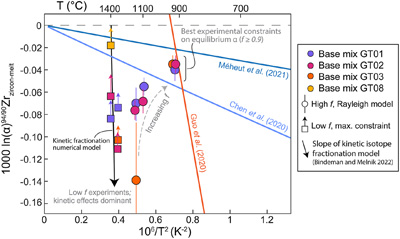 Figure 2 Temperature dependence of zircon-melt fractionation factors from ab initio studies (Chen et al., 2020; Méheut et al., 2021), natural samples (Guo et al., 2020), and our experiments. Circles are low T, high f experiments in Figure 1, from which Δ94/90Zr was retrieved using Rayleigh inversion. Squares denote high T, low f experiments, where only a maximum magnitude for fractionation (Δ94/90Zrapparent) in that experiment could be constrained (see text). Black solid line is the slope of kinetic isotope fractionation during diffusion limited growth of a zircon nucleating at 1400 °C, calculated using the numerical code of Bindeman and Melnik (2022) (see Supplementary Information for details). | 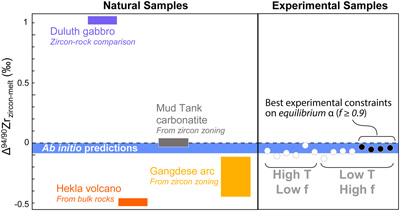 Figure 3 Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study). |
| Figure 1 | Figure 2 | Figure 3 |
top
Introduction
Zirconium (Zr) belongs to a group of transition metals known as the high field strength elements, which due to their distinctive geochemical properties are used to trace magmatic differentiation and the co-evolution of Earth’s mantle and crust. While studies of Zr stable isotope variation (expressed as δ94/90Zr = [(94Zr/90Zr)Sample/(94Zr/90Zr)Standard − 1]·1000) have all linked Zr isotopic variability to zircon crystallisation during magmatic differentiation, they have also yielded conflicting observations regarding the direction and magnitude of Zr isotope fractionation in magmatic systems. Based on a δ94/90Zr vs. SiO2 trend in volcanic rocks from Hekla, Iceland, Inglis et al. (2019)
Inglis, E.C., Moynier, F., Creech, J., Deng, Z., Day, J.M.D., Teng, F.Z., Bizzarro, M., Jackson, M., and Savage, P. (2019) Isotopic fractionation of zirconium during magmatic differentiation and the stable isotope composition of the silicate Earth. Geochimica Cosmochimica Acta 250, 311–323. https://doi.org/10.1016/j.gca.2019.02.010
suggested zircon is isotopically light compared to coexisting melt, and inferred a fractionation factor Δ94/90Zrzircon-melt (i.e. ≈1000·ln(αzircon-melt), where αzircon-melt = [(94Zr/90Zr)Zircon/(94Zr/90Zr)Melt]) of −0.5 ‰. Conversely, through measurement of single zircon and baddeleyite crystals from a gabbroic cumulate, Ibañez-Mejia and Tissot (2019)Ibañez-Mejia, M., and Tissot, F.L.H. (2019) Extreme Zr stable isotope fractionation during magmatic fractional crystallization. Science Advances 5, eaax8648. https://doi.org/10.1126/sciadv.aax8648
found these phases to be isotopically heavy relative to the starting melt using the bulk rock δ94/90Zr as a proxy, and inferred a Δ94/90Zrzircon-melt = 1.06 ‰. A subsequent study by Guo et al. (2020)Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
observed internally zoned zircon with isotopically light cores and progressively heavier rims, which they interpreted as equilibrium Rayleigh fractionation of isotopically light zircon from a melt with Δ94/90Zrzircon-melt between −0.12 and −0.45 ‰. However, in all studies conducted to date on natural samples, no co-existing zircon-glass pairs have been directly measured. Rather, zircon-melt fractionation factors have only been inferred by calculation (e.g., Rayleigh fitting or mass balance considerations).Adding to this conundrum, no resolvable δ94/90Zr variations (and therefore negligible fractionation) have been observed in several reference zircons (e.g., 91500, Mud Tank, and Plešovice; Tompkins et al., 2020
Tompkins, H.G.D., Zieman, L.J., Ibañez-Mejia, M., and Tissot, F.L.H. (2020) Zirconium stable isotope analysis of zircon by MC-ICP-MS: Methods and application to evaluating intra-crystalline zonation in a zircon megacryst. Journal of Analytical Atomic Spectrometry 35, 1167–1186. https://doi.org/10.1039/C9JA00315K
; Zhang et al., 2019Zhang, W., Wang, Z., Moynier, F., Inglis, E., Tian, S., Li, M., Liu, Y., and Hu, Z. (2019) Determination of Zr isotopic ratios in zircons using laser-Ablation multiple-collector inductively coupled-plasma mass-spectrometry. Journal of Analytical Atomic Spectrometry 34, 1800–1809. https://doi.org/10.1039/C9JA00192A
), and recent ab initio calculations by Chen et al. (2020)Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
and Méheut et al. (2021)Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
predict that the magnitude of equilibrium Zr isotope fractionation at magmatic temperatures is too small (Δ94/90Zrzircon-melt ≤ 0.08 ‰) to explain the large fractionations observed in natural systems. Instead, both theoretical studies concluded that a combination of equilibrium and kinetic fractionation processes during crystallisation of zircon and rock forming minerals is necessary to produce the large variations observed in natural igneous systems.Here, we address these conflicting observations from an experimental standpoint. Using zircon growth experiments performed under controlled laboratory conditions, we sought to determine the isotopic fractionation factor between zircon and melt (Δ94/90Zrzircon-melt; hereafter Δ94/90Zr for brevity) at various temperatures and melt compositions. To do so, experimental zircon and co-existing melts (quenched to a glass) were: 1) chemically separated using a novel sequential acid leaching procedure, and 2) their δ94/90Zr were measured at high accuracy and precision using a 91Zr-96Zr double spike method.
top
Experimental Procedure and Samples
We utilised run products from zircon growth experiments performed by Wang and Trail (2019)
Wang, Y., and Trail, D. (2019) Aluminum partitioning between zircon and haplogranitic melts: The influence of temperature and melt composition. Chemical Geology 511, 71–80. https://doi.org/10.1016/j.chemgeo.2019.02.016
and analysed: i) 11 experimental products published in Wang and Trail (2019)Wang, Y., and Trail, D. (2019) Aluminum partitioning between zircon and haplogranitic melts: The influence of temperature and melt composition. Chemical Geology 511, 71–80. https://doi.org/10.1016/j.chemgeo.2019.02.016
, ii) three ‘low temperature’ (925 °C) experiments also performed by Wang and Trail (2019)Wang, Y., and Trail, D. (2019) Aluminum partitioning between zircon and haplogranitic melts: The influence of temperature and melt composition. Chemical Geology 511, 71–80. https://doi.org/10.1016/j.chemgeo.2019.02.016
but previously unpublished because they produced zircon crystals too small for that study, and iii) homogenised fractions of four starting base mixes that represent the starting composition (i.e. bulk system) for all experiments. Zircon growth experiments were performed in a piston cylinder apparatus at various temperatures and melt compositions (Table S-1). Various synthetic mixtures (dubbed ‘base mixes’) were prepared to simulate a range of hydrous felsic melts in the SiO2-Al2O3-Na2O-K2O-CaO-ZrO2-H2O system with H2O fixed at ∼10 wt. % and doped with 500 ppm rubidium (Rb). Because Rb is highly incompatible in zircon, this trace element served as monitor for melt incorporation in the laser ablation study of Wang and Trail (2019)Wang, Y., and Trail, D. (2019) Aluminum partitioning between zircon and haplogranitic melts: The influence of temperature and melt composition. Chemical Geology 511, 71–80. https://doi.org/10.1016/j.chemgeo.2019.02.016
, and was used as proxy for zircon-melt chemical separation in this study (see Supplementary Information). The base mixes covered a range of aluminum saturation indices (ASI = molar ratio of Al2O3/[CaO + Na2O + K2O]) alkalinity indices (A/NK = molar ratio of Al2O3/[Na2O + K2O]) and M factors (M = molar ratio of [K + Na + 2Ca]/[Si × Al]), as these are useful criteria for characterising felsic rocks and parameterising zircon saturation in silicate melts (e.g., Boehnke et al., 2013Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., and Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334. https://doi.org/10.1016/j.chemgeo.2013.05.028
). Further details about the experiments and run products can be found in Wang and Trail (2019)Wang, Y., and Trail, D. (2019) Aluminum partitioning between zircon and haplogranitic melts: The influence of temperature and melt composition. Chemical Geology 511, 71–80. https://doi.org/10.1016/j.chemgeo.2019.02.016
.The experiments studied here cover a wide range of temperatures (1400 °C to 925 °C), ASI (0.9 to 1.3), A/NK (1.4 to 2.2) and M parameters (1.2 to 1.8) (Table S-1). In all cases, the experimental products consisted of a mixture of glass (quenched melt) and zircon. Since the zircon crystals in all experiments are too small (mostly ≤20 μm in diameter) to physically separate from the glass, we designed an extraction procedure using sequential acid leaching to attain full chemical separation of these phases. Our calibrated protocol resulted in complete separation of glass from zircon, enabling each fraction to be independently spiked and prepared for isotopic analysis. Once separation was achieved, all fractions were measured for their δ94/90Zr relative to the NIST standard using the analytical methods described in Tompkins et al. (2020)
Tompkins, H.G.D., Zieman, L.J., Ibañez-Mejia, M., and Tissot, F.L.H. (2020) Zirconium stable isotope analysis of zircon by MC-ICP-MS: Methods and application to evaluating intra-crystalline zonation in a zircon megacryst. Journal of Analytical Atomic Spectrometry 35, 1167–1186. https://doi.org/10.1039/C9JA00315K
. Analytical methods are summarised in the Supplementary Information.For each experimental product, we determined the total mass fraction of Zr removed from the liquid in the form of zircon relative to the bulk initial (i.e. f factor). Mean f values and their variability within the liquid at the time of quenching were determined in situ using Zr concentration measurements in glass fragments via secondary ion mass spectrometry (SIMS). The mean and variability in f values assigned in this manner were used to propagate uncertainties through all subsequent calculations. To ensure consistency, the mean f values determined using SIMS measurements of glass were verified using Zr/Rb measurements from solutions produced after acid leaching of glasses during preparation for isotopic analyses. Details about methods and calculations are included in the Supplementary Information.
top
Results
Results from all our measurements are reported in Tables S-2, S-3, and shown graphically in Figure 1. Experiments were found to yield mean f values between 0.12 ± 0.06 and 0.97 ± 0.01. The δ94/90Zr of the four base mixes were undistinguishable within uncertainty, and their mean value (0.054 ± 0.005 ‰) is depicted in Figure 1a (horizontal grey band). Results for all 14 zircon-glass pairs analysed are shown ranked by increasing mean f. All zircon fractions exhibit lower δ94/90Zr with respect to the bulk system, ranging from −0.168 ± 0.011 ‰ to −0.068 ± 0.013 ‰. In contrast, glasses have a bimodal δ94/90Zr distribution; six high temperature (1300 – 1400 °C) experiments yielded mean f ≤ 0.53 and glass δ94/90Zr values indistinguishable from the bulk system within uncertainty (−0.057 ± 0.016 ‰ to −0.050 ± 0.013 ‰), while the eight experiments conducted at lower temperatures (925 – 1150 °C) yielded mean f ≥ 0.78 and positive glass δ94/90Zr values (−0.004 ± 0.013 ‰ to +0.123 ± 0.013 ‰) compared to the bulk. Isotopic mixing calculations performed using the δ94/90Zr and f determined for each glass-zircon pair show excellent agreement within uncertainty with respect to the δ94/90Zr value of the starting base mix, thus confirming mass balance (Fig. 1b).

Figure 1 (a) δ94/90Zr of the glass (orange) and bulk zircon (blue) for each experiment. ‘Bulk system’ is the mean value of all experimental base mixes. (b) Mass balance calculations for all glass-zircon pairs compared to the δ94/90Zr of the bulk starting mix. (c) Apparent Δ94/90Zr, the fractionation factor between zircon and melt, determined for each experiment (see text for further details and discussion). Range of ab initio values between 1300 °C and 700 °C (Chen et al., 2020
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
; Méheut et al., 2021Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
) are shown as horizontal blue bands. Samples are shown rank ordered by increasing mean f. Uncertainties, visible only when larger than the symbols, are 2σ.top
Discussion
The diffusivity of Zr4+ in zircon is expected to be extremely low even at magmatic temperatures (Cherniak et al., 1997
Cherniak, D.J., Hanchar, J.M., and Watson, E.B. (1997) Diffusion of tetravalent cations in zircon. Contributions to Mineralogy and Petrology 127, 383–390. https://doi.org/10.1007/s004100050287
; Ibañez-Mejia and Tissot, 2019Ibañez-Mejia, M., and Tissot, F.L.H. (2019) Extreme Zr stable isotope fractionation during magmatic fractional crystallization. Science Advances 5, eaax8648. https://doi.org/10.1126/sciadv.aax8648
). Therefore, the growth of zircon from a magma removes Zr as a Rayleigh-type process even if chemical and isotopic equilibrium partitioning between the solid and melt are maintained, where only the outermost rim of the crystal is in equilibrium with the immediately surrounding melt while interior domains of the zircon become isolated from the rest of the system (Criss, 1999Criss, R.E. (1999) Principles of Stable Isotope Distribution. Oxford Univ Press, New York. https://doi.org/10.1093/oso/9780195117752.001.0001
). In an equilibrium Rayleigh scenario, one could directly recover Δ94/90Zr from experiments by measuring the isotopic composition of the outermost zircon rim and melt in direct equilibrium, but this is impossible to achieve using our experimental setup. Instead, our chemical separation method produces bulk glass and bulk (i.e. cumulative) zircon fractions, meaning that we can only capture the total integrated isotopic effects that a Rayleigh-type process imposes on δ94/90Zr over the entire f interval of the experiment.To approximate Δ94/90Zr using the results of Figure 1a, we took an inverse approach that treats each zircon crystallisation experiment as an equilibrium Rayleigh fractionation. The recovered Δ94/90Zr are summarised in Figure 1c, where they are compared with theoretically predicted values at 1300 – 700 °C from ab initio calculations. While all but one of our experiments conform to mass balance (Fig. 1b), for most high T experiments (low f) the δ94/90Zr of the zircon, glass, and bulk system could not all be exactly fitted using an equilibrium Rayleigh fractionation inversion. For experiments where f ≤ 0.53, zircon fractions have δ94/90Zr values that are ‘too low’ for their respective mean f if an equilibrium process is assumed. For these experiments, we used the absolute difference in δ94/90Zr between the glass and bulk zircon measurements (a parameter we refer to as Δ94/90Zrapparent), as a maximum permissible limit for the Δ94/90Zr governing that experiment (see Supplementary Information for a detailed rationale of this approach).
In general, all of the Δ94/90Zrapparent values determined from high T (low f) experiments, as well as the best fit Δ94/90Zr values from Rayleigh inversion of low T (high f) experiments, indicate that: i) zircon is invariably isotopically light relative to the melt from which it precipitates, and ii) that the magnitude of the fractionation factor between zircon and melt (Δ94/90Zr) is always smaller than −0.139 ‰ over the experimental temperature range. Details of the mathematical approach and parameters used to estimate Δ94/90Zr and calculate uncertainties are included in the Supplementary Information.
To explore whether temperature and/or melt compositional differences are controlling the variable fractionations observed between experiments, Figure 2 shows the fractionation results of Figure 1c plotted as a function of their inverse squared temperature. The ab initio zircon fractionation models of Chen et al. (2020)
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
(relative to Ca-catapleiite) and Meheut et al. (2021)Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
(relative to gittinsite) are shown for comparison, as well as the model of Guo et al. (2020)Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
, obtained from Rayleigh inversion of δ94/90Zr zoning in natural zircon. It is important to note, however, that because the Guo et al. (2020)Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
model does not result in a Δ94/90Zr = 0 at infinite temperature (i.e. 1/T2 = 0), it has little physical meaning and, unlike as argued in that study, cannot represent an equilibrium fractionation process (Schauble et al., 2009Schauble, E.A., Méheut, M., and Hill, P.S. (2009) Combining Metal Stable Isotope Fractionation Theory with Experiments. Elements 5, 369–374. https://doi.org/10.2113/gselements.5.6.369
; Young et al., 2015Young, E.D., Manning, C.E., Schauble, E.A., Shahar, A., Macris, C.A., Lazar, C., and Jordan, M. (2015) High-temperature equilibrium isotope fractionation of non-traditional stable isotopes: Experiments, theory, and applications. Chemical Geology 395, 176–195. https://doi.org/10.1016/j.chemgeo.2014.12.013
).
Figure 2 Temperature dependence of zircon-melt fractionation factors from ab initio studies (Chen et al., 2020
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
; Méheut et al., 2021Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
), natural samples (Guo et al., 2020Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
), and our experiments. Circles are low T, high f experiments in Figure 1, from which Δ94/90Zr was retrieved using Rayleigh inversion. Squares denote high T, low f experiments, where only a maximum magnitude for fractionation (Δ94/90Zrapparent) in that experiment could be constrained (see text). Black solid line is the slope of kinetic isotope fractionation during diffusion limited growth of a zircon nucleating at 1400 °C, calculated using the numerical code of Bindeman and Melnik (2022)Bindeman, I.N. and Melnik, O.E. (2022) The rises and falls of zirconium isotopes during zircon crystallisation. Geochemical Perspectives Letters 24, 17–21. https://doi.org/10.7185/geochemlet.2241
(see Supplementary Information for details).Close inspection of Figure 2 reveals that our data do not plot along a single slope in Δ94/90Zr vs. 1/T2 space, which clearly indicates that effects other than equilibrium isotope partitioning are influencing the Δ94/90Zr values calculated from our experiments. Because no arrays that are co-linear with the origin of this plot are defined among experiments sharing any given base mix, the scatter is unlikely to be caused by a melt chemistry dependence (e.g., variable M, ASI or A/NK) of the fractionation factor. Our high T experiments exhibit the largest Δ94/90Zr scatter at any given T and define a steep array with a slope indicative of non-equilibrium fractionation.
Non-equilibrium trace element and isotope partitioning is expected to develop in solids growing from a magma when the distribution coefficient (KD = [i]solid/[i]liquid) of a species of interest [i] diverges from unity, with the magnitude of the effects increasing proportionally to the ratio of phase boundary migration velocity over the diffusivity of the species in question (Albarede and Bottinga, 1972
Albarede, F. and Bottinga, Y. (1972) Kinetic disequilibrium in trace element partitioning between phenocrysts and host lava. Geochimica Cosmochimica Acta 36, 141–156. https://doi.org/10.1016/0016-7037(72)90003-8
; Watson and Müller, 2009Watson, E.B., and Müller, T. (2009) Non-equilibrium isotopic and elemental fractionation during diffusion-controlled crystal growth under static and dynamic conditions. Chemical Geology 267, 111–124. https://doi.org/10.1016/j.chemgeo.2008.10.036
; Watkins et al., 2017Watkins, J.M., DePaolo, D.J., and Watson, E.B. (2017) Kinetic fractionation of non-traditional stable isotopes by diffusion and crystal growth reactions. Reviews in Mineralogy and Geochemistry 82, 85–125. https://doi.org/10.2138/rmg.2017.82.4
). Although analytical expressions to quantify this process in radial coordinates exist (e.g., Eq. 11 of Watson and Müller, 2009Watson, E.B., and Müller, T. (2009) Non-equilibrium isotopic and elemental fractionation during diffusion-controlled crystal growth under static and dynamic conditions. Chemical Geology 267, 111–124. https://doi.org/10.1016/j.chemgeo.2008.10.036
), these are not applicable to the case of zircon growth as the conditions for this process are outside the bounds over which the Watson and Müller (2009)Watson, E.B., and Müller, T. (2009) Non-equilibrium isotopic and elemental fractionation during diffusion-controlled crystal growth under static and dynamic conditions. Chemical Geology 267, 111–124. https://doi.org/10.1016/j.chemgeo.2008.10.036
relationships are accurate (i.e. these apply for trace species where KD < ≈0.5). Thus, at present, the magnitude of Zr isotope fractionation during diffusion limited growth of magmatic zircon is better approached numerically.To test for a possible kinetic control on isotope fractionation in our experiments, we used the numerical approach of Bindeman and Melnik (2022)
Bindeman, I.N. and Melnik, O.E. (2022) The rises and falls of zirconium isotopes during zircon crystallisation. Geochemical Perspectives Letters 24, 17–21. https://doi.org/10.7185/geochemlet.2241
to calculate an expected Δ94/90Zr vs. 1/T2 relation for zircon nucleating at 1400 °C and using model parameters close to those of our experimental conditions (see Supplementary Information). Because β factors (an empirical parameter describing the efficiency of diffusive isotope fractionation; Richter et al., 1999Richter, F.M., Liang, Y., and Davis, A.M. (1999) Isotope fractionation by diffusion in molten oxides. Geochimica Cosmochimica Acta 63, 2853–2861. https://doi.org/10.1016/S0016-7037(99)00164-7
) for Zr in melt have not yet been determined, we do not attempt to reproduce our experiments quantitatively. However, it can be clearly seen from Figure 2 that the slope of kinetic isotope fractionation in Δ94/90Zr vs. 1/T2 space closely resembles the trend defined by our high T experiments, and is also similar to the slope of the Guo et al. (2020)Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
model defined using natural zircon nucleated at lower temperatures. Thus, we interpret these steep arrays that do not intersect the origin of a Δ94/90Zr vs. 1/T2 plot as reflecting a combination of equilibrium and kinetic isotope fractionation effects, resulting in a compounded, larger fractionation than what can be imparted by vibrational equilibrium processes alone. Nevertheless, because β factors for Zr remain unknown, quantitative deconvolution of kinetic and equilibrium fractionation contributions to natural and experimental Δ94/90Zr data is not yet possible.Given the above observations, we consider the experiments performed at high T (low f) inadequate for quantifying an equilibrium fractionation coefficient, and instead argue that the results from our highest f experiments (n = 4 where f ≥ 0.9)) yield the Δ94/90Zr that most closely approach the magnitude of the equilibrium fractionation factor. Indeed, isotope effects recorded by a solid growing in a kinetically dominated system where KD >> 1 are significant at low f (e.g., Fig. 12 of Watson and Müller, 2009
Watson, E.B., and Müller, T. (2009) Non-equilibrium isotopic and elemental fractionation during diffusion-controlled crystal growth under static and dynamic conditions. Chemical Geology 267, 111–124. https://doi.org/10.1016/j.chemgeo.2008.10.036
), whereas the impact of kinetic fractionation on the cumulative solid composition must, by mass balance, approach zero as f tends to unity. Results from experiments where f ≥ 0.9 yield a mean Δ94/90Zr of −0.045 ‰. Although these experiments can potentially also be affected to some small degree by kinetic isotope effects, they all tightly cluster between the Δ94/90Zr models of Chen et al. (2020)Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
and Méheut et al. (2021)Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
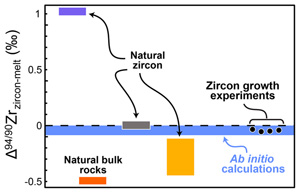
(Fig. 2), supporting the accuracy of these first principles calculations. While our results cannot distinguish which of these two theoretical models is more accurate, we note that the absolute difference in Δ94/90Zr at magmatic T between these studies is exceedingly small. As such, our results experimentally confirm their predictions, and reinforce the notion that large fractionations observed in natural zircon cannot be the result of equilibrium fractionation processes.Overall, our results are in excellent agreement with the direction of isotopic fractionation estimated from ab initio studies and, for our lowest T experiments (f ≥ 0.9), also its magnitude. Our results thus confirm that the expected effects of equilibrium isotope fractionation during magmatic zircon crystallisation are exceedingly small, demonstrating that the observed range of natural variability cannot be explained by this mechanism (Fig. 3). Instead, and as argued by Chen et al. (2020)
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
, Méheut et al. (2021)Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
, and Tissot and Ibañez-Mejia (2021)Tissot, F.L.H., and Ibañez-Mejia, M. (2021) Unlocking the single-crystal record of heavy stable isotopes. Elements 17 (6), 389–394. https://doi.org/10.2138/gselements.17.6.389
, we conclude that non-equilibrium effects are needed to explain, and must be the dominant driver of, the large Zr isotope variations observed in natural systems.
Figure 3 Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
; Méheut et al., 2021Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
), natural samples (Ibañez-Mejia and Tissot, 2019Ibañez-Mejia, M., and Tissot, F.L.H. (2019) Extreme Zr stable isotope fractionation during magmatic fractional crystallization. Science Advances 5, eaax8648. https://doi.org/10.1126/sciadv.aax8648
; Inglis et al., 2019Inglis, E.C., Moynier, F., Creech, J., Deng, Z., Day, J.M.D., Teng, F.Z., Bizzarro, M., Jackson, M., and Savage, P. (2019) Isotopic fractionation of zirconium during magmatic differentiation and the stable isotope composition of the silicate Earth. Geochimica Cosmochimica Acta 250, 311–323. https://doi.org/10.1016/j.gca.2019.02.010
; Guo et al., 2020Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
; Tompkins et al., 2020Tompkins, H.G.D., Zieman, L.J., Ibañez-Mejia, M., and Tissot, F.L.H. (2020) Zirconium stable isotope analysis of zircon by MC-ICP-MS: Methods and application to evaluating intra-crystalline zonation in a zircon megacryst. Journal of Analytical Atomic Spectrometry 35, 1167–1186. https://doi.org/10.1039/C9JA00315K
), and experimental samples (this study).top
Conclusions and Implications
This study demonstrates that: 1) at equilibrium, zircon is isotopically light compared to its co-existing silicic melt; 2) the magnitude of equilibrium Zr isotope fractionation between zircon and melt at magmatic temperatures is extremely small (Δ94/90Zr ≈ −0.045 ‰), as predicted by ab initio calculations; and 3) the large δ94/90Zr variations observed in natural igneous systems to date are not the result of equilibrium fractionation during zircon crystallisation. Our results reinforce the notion that kinetic isotope effects play a central, if not the dominant, role in fractionating Zr isotopes in high temperature environments. Thus, additional experimental constraints that quantify the magnitude of kinetic separation of Zr isotopes in solids and liquids (e.g., Watkins et al., 2017
Watkins, J.M., DePaolo, D.J., and Watson, E.B. (2017) Kinetic fractionation of non-traditional stable isotopes by diffusion and crystal growth reactions. Reviews in Mineralogy and Geochemistry 82, 85–125. https://doi.org/10.2138/rmg.2017.82.4
) are needed before the fractionations observed in natural systems can be fully understood and quantified.top
Acknowledgements
This project was supported by NSF Graduate Research Fellowship award DGE-1746060, an MSA Student Research Grant, and a GSA Student Research Grant (to HGDT), as well as NSF-EAR grants 2131632 and 2143168 (to MIM), 1824002 (to FLHT), 1650033 (to DT), and SNSF Ambizione grant PZ00P2_173988 (to EB). FLHT acknowledges additional support from NSF grant MGG-2054892, a Packard Fellowship, a research award from the Heritage Medical Research Institute, and startup funds from Caltech. The authors thank editor Anat Shahar, James Van Orman, and an anonymous reviewer, for constructive reviews that improved the clarity of this article.
Editor: Anat Shahar
top
References
Albarede, F. and Bottinga, Y. (1972) Kinetic disequilibrium in trace element partitioning between phenocrysts and host lava. Geochimica Cosmochimica Acta 36, 141–156. https://doi.org/10.1016/0016-7037(72)90003-8
 Show in context
Show in context Non-equilibrium trace element and isotope partitioning is expected to develop in solids growing from a magma when the distribution coefficient (KD = [i]solid/[i]liquid) of a species of interest [i] diverges from unity, with the magnitude of the effects increasing proportionally to the ratio of phase boundary migration velocity over the diffusivity of the species in question (Albarede and Bottinga, 1972; Watson and Müller, 2009; Watkins et al., 2017).
View in article
Bindeman, I.N. and Melnik, O.E. (2022) The rises and falls of zirconium isotopes during zircon crystallisation. Geochemical Perspectives Letters 24, 17–21. https://doi.org/10.7185/geochemlet.2241
 Show in context
Show in context Black solid line is the slope of kinetic isotope fractionation during diffusion limited growth of a zircon nucleating at 1400 °C, calculated using the numerical code of Bindeman and Melnik (2022) (see Supplementary Information for details).
View in article
To test for a possible kinetic control on isotope fractionation in our experiments, we used the numerical approach of Bindeman and Melnik (2022) to calculate an expected Δ94/90Zr vs. 1/T2 relation for zircon nucleating at 1400 °C and using model parameters close to those of our experimental conditions (see Supplementary Information).
View in article
Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., and Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334. https://doi.org/10.1016/j.chemgeo.2013.05.028
 Show in context
Show in context The base mixes covered a range of aluminum saturation indices (ASI = molar ratio of Al2O3/[CaO + Na2O + K2O]) alkalinity indices (A/NK = molar ratio of Al2O3/[Na2O + K2O]) and M factors (M = molar ratio of [K + Na + 2Ca]/[Si × Al]), as these are useful criteria for characterising felsic rocks and parameterising zircon saturation in silicate melts (e.g., Boehnke et al., 2013).
View in article
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
 Show in context
Show in context Adding to this conundrum, no resolvable δ94/90Zr variations (and therefore negligible fractionation) have been observed in several reference zircons (e.g., 91500, Mud Tank, and Plešovice; Tompkins et al., 2020; Zhang et al., 2019), and recent ab initio calculations by Chen et al. (2020) and Méheut et al. (2021) predict that the magnitude of equilibrium Zr isotope fractionation at magmatic temperatures is too small (Δ94/90Zrzircon-melt ≤ 0.08 ‰) to explain the large fractionations observed in natural systems.
View in article
Range of ab initio values between 1300 °C and 700 °C (Chen et al., 2020; Méheut et al., 2021) are shown as horizontal blue bands.
View in article
The ab initio zircon fractionation models of Chen et al. (2020) (relative to Ca-catapleiite) and Meheut et al. (2021) (relative to gittinsite) are shown for comparison, as well as the model of Guo et al. (2020), obtained from Rayleigh inversion of δ94/90Zr zoning in natural zircon.
View in article
Temperature dependence of zircon-melt fractionation factors from ab initio studies (Chen et al., 2020; Méheut et al., 2021), natural samples (Guo et al., 2020), and our experiments.
View in article
Although these experiments can potentially also be affected to some small degree by kinetic isotope effects, they all tightly cluster between the Δ94/90Zr models of Chen et al. (2020) and Méheut et al. (2021) (Fig. 2), supporting the accuracy of these first principles calculations.
View in article
Instead, and as argued by Chen et al. (2020), Méheut et al. (2021), and Tissot and Ibañez-Mejia (2021), we conclude that non-equilibrium effects are needed to explain, and must be the dominant driver of, the large Zr isotope variations observed in natural systems.
View in article
Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study).
View in article
Cherniak, D.J., Hanchar, J.M., and Watson, E.B. (1997) Diffusion of tetravalent cations in zircon. Contributions to Mineralogy and Petrology 127, 383–390. https://doi.org/10.1007/s004100050287
 Show in context
Show in context The diffusivity of Zr4+ in zircon is expected to be extremely low even at magmatic temperatures (Cherniak et al., 1997; Ibañez-Mejia and Tissot, 2019).
View in article
Criss, R.E. (1999) Principles of Stable Isotope Distribution. Oxford Univ Press, New York. https://doi.org/10.1093/oso/9780195117752.001.0001
 Show in context
Show in context Therefore, the growth of zircon from a magma removes Zr as a Rayleigh-type process even if chemical and isotopic equilibrium partitioning between the solid and melt are maintained, where only the outermost rim of the crystal is in equilibrium with the immediately surrounding melt while interior domains of the zircon become isolated from the rest of the system (Criss, 1999).
View in article
Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
 Show in context
Show in context A subsequent study by Guo et al. (2020) observed internally zoned zircon with isotopically light cores and progressively heavier rims, which they interpreted as equilibrium Rayleigh fractionation of isotopically light zircon from a melt with Δ94/90Zrzircon-melt between −0.12 and −0.45 ‰.
View in article
The ab initio zircon fractionation models of Chen et al. (2020) (relative to Ca-catapleiite) and Meheut et al. (2021) (relative to gittinsite) are shown for comparison, as well as the model of Guo et al. (2020), obtained from Rayleigh inversion of δ94/90Zr zoning in natural zircon.
View in article
It is important to note, however, that because the Guo et al. (2020) model does not result in a Δ94/90Zr = 0 at infinite temperature (i.e. 1/T2 = 0), it has little physical meaning and, unlike as argued in that study, cannot represent an equilibrium fractionation process (Schauble et al., 2009; Young et al., 2015).
View in article
Temperature dependence of zircon-melt fractionation factors from ab initio studies (Chen et al., 2020; Méheut et al., 2021), natural samples (Guo et al., 2020), and our experiments.
View in article
However, it can be clearly seen from Figure 2 that the slope of kinetic isotope fractionation in Δ94/90Zr vs. 1/T2 space closely resembles the trend defined by our high T experiments, and is also similar to the slope of the Guo et al. (2020) model defined using natural zircon nucleated at lower temperatures.
View in article
Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study).
View in article
Ibañez-Mejia, M., and Tissot, F.L.H. (2019) Extreme Zr stable isotope fractionation during magmatic fractional crystallization. Science Advances 5, eaax8648. https://doi.org/10.1126/sciadv.aax8648
 Show in context
Show in context Conversely, through measurement of single zircon and baddeleyite crystals from a gabbroic cumulate, Ibañez-Mejia and Tissot (2019) found these phases to be isotopically heavy relative to the starting melt using the bulk rock δ94/90Zr as a proxy, and inferred a Δ94/90Zrzircon-melt = 1.06 ‰.
View in article
The diffusivity of Zr4+ in zircon is expected to be extremely low even at magmatic temperatures (Cherniak et al., 1997; Ibañez-Mejia and Tissot, 2019).
View in article
Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study).
View in article
Inglis, E.C., Moynier, F., Creech, J., Deng, Z., Day, J.M.D., Teng, F.Z., Bizzarro, M., Jackson, M., and Savage, P. (2019) Isotopic fractionation of zirconium during magmatic differentiation and the stable isotope composition of the silicate Earth. Geochimica Cosmochimica Acta 250, 311–323. https://doi.org/10.1016/j.gca.2019.02.010
 Show in context
Show in context Based on a δ94/90Zr vs. SiO2 trend in volcanic rocks from Hekla, Iceland, Inglis et al. (2019) suggested zircon is isotopically light compared to coexisting melt, and inferred a fractionation factor Δ94/90Zrzircon-melt (i.e. ≈1000·ln(αzircon-melt), where αzircon-melt = [(94Zr/90Zr)Zircon/(94Zr/90Zr)Melt]) of −0.5 ‰.
View in article
Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study).
View in article
Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
 Show in context
Show in context
Adding to this conundrum, no resolvable δ94/90Zr variations (and therefore negligible fractionation) have been observed in several reference zircons (e.g., 91500, Mud Tank, and Plešovice; Tompkins et al., 2020; Zhang et al., 2019), and recent ab initio calculations by Chen et al. (2020) and Méheut et al. (2021) predict that the magnitude of equilibrium Zr isotope fractionation at magmatic temperatures is too small (Δ94/90Zrzircon-melt ≤ 0.08 ‰) to explain the large fractionations observed in natural systems.
View in article
Range of ab initio values between 1300 °C and 700 °C (Chen et al., 2020; Méheut et al., 2021) are shown as horizontal blue bands.
View in article
The ab initio zircon fractionation models of Chen et al. (2020) (relative to Ca-catapleiite) and Meheut et al. (2021) (relative to gittinsite) are shown for comparison, as well as the model of Guo et al. (2020), obtained from Rayleigh inversion of δ94/90Zr zoning in natural zircon.
View in article
Temperature dependence of zircon-melt fractionation factors from ab initio studies (Chen et al., 2020; Méheut et al., 2021), natural samples (Guo et al., 2020), and our experiments.
View in article
Although these experiments can potentially also be affected to some small degree by kinetic isotope effects, they all tightly cluster between the Δ94/90Zr models of Chen et al. (2020) and Méheut et al. (2021) (Fig. 2), supporting the accuracy of these first principles calculations.
View in article
Instead, and as argued by Chen et al. (2020), Méheut et al. (2021), and Tissot and Ibañez-Mejia (2021), we conclude that non-equilibrium effects are needed to explain, and must be the dominant driver of, the large Zr isotope variations observed in natural systems.
View in article
Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study).
View in article
Richter, F.M., Liang, Y., and Davis, A.M. (1999) Isotope fractionation by diffusion in molten oxides. Geochimica Cosmochimica Acta 63, 2853–2861. https://doi.org/10.1016/S0016-7037(99)00164-7
 Show in context
Show in context Because β factors (an empirical parameter describing the efficiency of diffusive isotope fractionation; Richter et al., 1999) for Zr in melt have not yet been determined, we do not attempt to reproduce our experiments quantitatively.
View in article
Schauble, E.A., Méheut, M., and Hill, P.S. (2009) Combining Metal Stable Isotope Fractionation Theory with Experiments. Elements 5, 369–374. https://doi.org/10.2113/gselements.5.6.369
 Show in context
Show in context It is important to note, however, that because the Guo et al. (2020) model does not result in a Δ94/90Zr = 0 at infinite temperature (i.e. 1/T2 = 0), it has little physical meaning and, unlike as argued in that study, cannot represent an equilibrium fractionation process (Schauble et al., 2009; Young et al., 2015).
View in article
Tissot, F.L.H., and Ibañez-Mejia, M. (2021) Unlocking the single-crystal record of heavy stable isotopes. Elements 17 (6), 389–394. https://doi.org/10.2138/gselements.17.6.389
 Show in context
Show in context Instead, and as argued by Chen et al. (2020), Méheut et al. (2021), and Tissot and Ibañez-Mejia (2021), we conclude that non-equilibrium effects are needed to explain, and must be the dominant driver of, the large Zr isotope variations observed in natural systems.
View in article
Tompkins, H.G.D., Zieman, L.J., Ibañez-Mejia, M., and Tissot, F.L.H. (2020) Zirconium stable isotope analysis of zircon by MC-ICP-MS: Methods and application to evaluating intra-crystalline zonation in a zircon megacryst. Journal of Analytical Atomic Spectrometry 35, 1167–1186. https://doi.org/10.1039/C9JA00315K
 Show in context
Show in context Adding to this conundrum, no resolvable δ94/90Zr variations (and therefore negligible fractionation) have been observed in several reference zircons (e.g., 91500, Mud Tank, and Plešovice; Tompkins et al., 2020; Zhang et al., 2019), and recent ab initio calculations by Chen et al. (2020) and Méheut et al. (2021) predict that the magnitude of equilibrium Zr isotope fractionation at magmatic temperatures is too small (Δ94/90Zrzircon-melt ≤ 0.08 ‰) to explain the large fractionations observed in natural systems.
View in article
Once separation was achieved, all fractions were measured for their δ94/90Zr relative to the NIST standard using the analytical methods described in Tompkins et al. (2020).
View in article
Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020; Méheut et al., 2021), natural samples (Ibañez-Mejia and Tissot, 2019; Inglis et al., 2019; Guo et al., 2020; Tompkins et al., 2020), and experimental samples (this study).
View in article
Wang, Y., and Trail, D. (2019) Aluminum partitioning between zircon and haplogranitic melts: The influence of temperature and melt composition. Chemical Geology 511, 71–80. https://doi.org/10.1016/j.chemgeo.2019.02.016
 Show in context
Show in context We utilised run products from zircon growth experiments performed by Wang and Trail (2019) and analysed: i) 11 experimental products published in Wang and Trail (2019), ii) three ‘low temperature’ (925 °C) experiments also performed by Wang and Trail (2019) but previously unpublished because they produced zircon crystals too small for that study, and iii) homogenised fractions of four starting base mixes that represent the starting composition (i.e. bulk system) for all experiments.
View in article
Because Rb is highly incompatible in zircon, this trace element served as monitor for melt incorporation in the laser ablation study of Wang and Trail (2019), and was used as proxy for zircon-melt chemical separation in this study (see Supplementary Information).
View in article
Further details about the experiments and run products can be found in Wang and Trail (2019).
View in article
Watkins, J.M., DePaolo, D.J., and Watson, E.B. (2017) Kinetic fractionation of non-traditional stable isotopes by diffusion and crystal growth reactions. Reviews in Mineralogy and Geochemistry 82, 85–125. https://doi.org/10.2138/rmg.2017.82.4
 Show in context
Show in context Non-equilibrium trace element and isotope partitioning is expected to develop in solids growing from a magma when the distribution coefficient (KD = [i]solid/[i]liquid) of a species of interest [i] diverges from unity, with the magnitude of the effects increasing proportionally to the ratio of phase boundary migration velocity over the diffusivity of the species in question (Albarede and Bottinga, 1972; Watson and Müller, 2009; Watkins et al., 2017).
View in article
Thus, additional experimental constraints that quantify the magnitude of kinetic separation of Zr isotopes in solids and liquids (e.g., Watkins et al., 2017) are needed before the fractionations observed in natural systems can be fully understood and quantified.
View in article
Watson, E.B., and Müller, T. (2009) Non-equilibrium isotopic and elemental fractionation during diffusion-controlled crystal growth under static and dynamic conditions. Chemical Geology 267, 111–124. https://doi.org/10.1016/j.chemgeo.2008.10.036
 Show in context
Show in context Non-equilibrium trace element and isotope partitioning is expected to develop in solids growing from a magma when the distribution coefficient (KD = [i]solid/[i]liquid) of a species of interest [i] diverges from unity, with the magnitude of the effects increasing proportionally to the ratio of phase boundary migration velocity over the diffusivity of the species in question (Albarede and Bottinga, 1972; Watson and Müller, 2009; Watkins et al., 2017).
View in article
Although analytical expressions to quantify this process in radial coordinates exist (e.g., Eq. 11 of Watson and Müller, 2009), these are not applicable to the case of zircon growth as the conditions for this process are outside the bounds over which the Watson and Müller (2009) relationships are accurate (i.e. these apply for trace species where KD < ≈0.5).
View in article
Indeed, isotope effects recorded by a solid growing in a kinetically dominated system where KD >> 1 are significant at low f (e.g., Fig. 12 of Watson and Müller, 2009), whereas the impact of kinetic fractionation on the cumulative solid composition must, by mass balance, approach zero as f tends to unity.
View in article
Young, E.D., Manning, C.E., Schauble, E.A., Shahar, A., Macris, C.A., Lazar, C., and Jordan, M. (2015) High-temperature equilibrium isotope fractionation of non-traditional stable isotopes: Experiments, theory, and applications. Chemical Geology 395, 176–195. https://doi.org/10.1016/j.chemgeo.2014.12.013
 Show in context
Show in context It is important to note, however, that because the Guo et al. (2020) model does not result in a Δ94/90Zr = 0 at infinite temperature (i.e. 1/T2 = 0), it has little physical meaning and, unlike as argued in that study, cannot represent an equilibrium fractionation process (Schauble et al., 2009; Young et al., 2015).
View in article
Zhang, W., Wang, Z., Moynier, F., Inglis, E., Tian, S., Li, M., Liu, Y., and Hu, Z. (2019) Determination of Zr isotopic ratios in zircons using laser-Ablation multiple-collector inductively coupled-plasma mass-spectrometry. Journal of Analytical Atomic Spectrometry 34, 1800–1809. https://doi.org/10.1039/C9JA00192A
 Show in context
Show in context Adding to this conundrum, no resolvable δ94/90Zr variations (and therefore negligible fractionation) have been observed in several reference zircons (e.g., 91500, Mud Tank, and Plešovice; Tompkins et al., 2020; Zhang et al., 2019), and recent ab initio calculations by Chen et al. (2020) and Méheut et al. (2021) predict that the magnitude of equilibrium Zr isotope fractionation at magmatic temperatures is too small (Δ94/90Zrzircon-melt ≤ 0.08 ‰) to explain the large fractionations observed in natural systems.
View in article
top
Supplementary Information
The Supplementary Information includes:
Download the Supplementary Information (PDF)
Figures
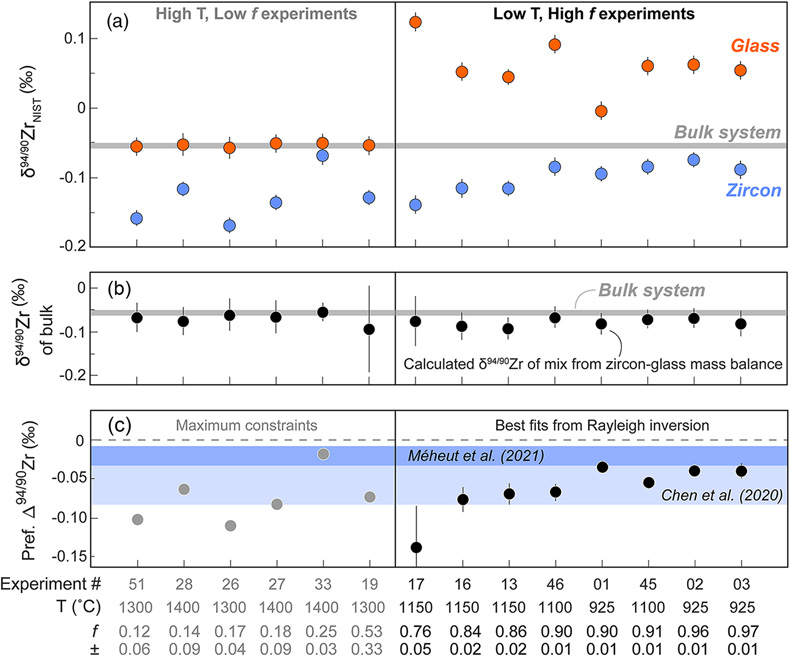
Figure 1 (a) δ94/90Zr of the glass (orange) and bulk zircon (blue) for each experiment. ‘Bulk system’ is the mean value of all experimental base mixes. (b) Mass balance calculations for all glass-zircon pairs compared to the δ94/90Zr of the bulk starting mix. (c) Apparent Δ94/90Zr, the fractionation factor between zircon and melt, determined for each experiment (see text for further details and discussion). Range of ab initio values between 1300 °C and 700 °C (Chen et al., 2020
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
; Méheut et al., 2021Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
) are shown as horizontal blue bands. Samples are shown rank ordered by increasing mean f. Uncertainties, visible only when larger than the symbols, are 2σ.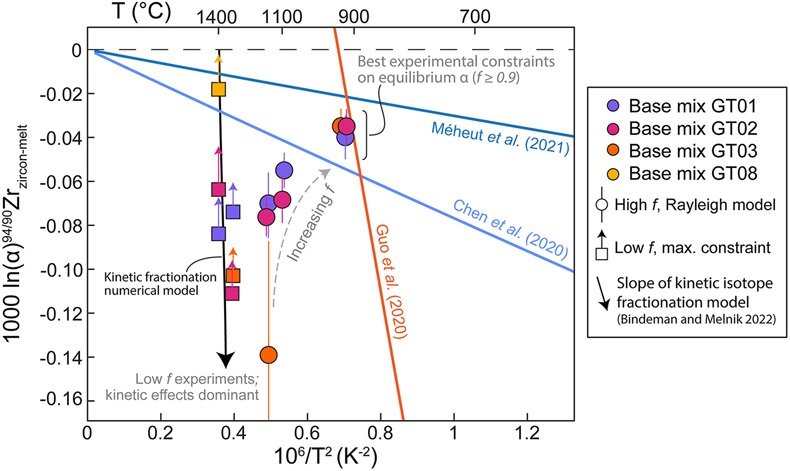
Figure 2 Temperature dependence of zircon-melt fractionation factors from ab initio studies (Chen et al., 2020
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
; Méheut et al., 2021Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
), natural samples (Guo et al., 2020Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
), and our experiments. Circles are low T, high f experiments in Figure 1, from which Δ94/90Zr was retrieved using Rayleigh inversion. Squares denote high T, low f experiments, where only a maximum magnitude for fractionation (Δ94/90Zrapparent) in that experiment could be constrained (see text). Black solid line is the slope of kinetic isotope fractionation during diffusion limited growth of a zircon nucleating at 1400 °C, calculated using the numerical code of Bindeman and Melnik (2022)Bindeman, I.N. and Melnik, O.E. (2022) The rises and falls of zirconium isotopes during zircon crystallisation. Geochemical Perspectives Letters 24, 17–21. https://doi.org/10.7185/geochemlet.2241
(see Supplementary Information for details).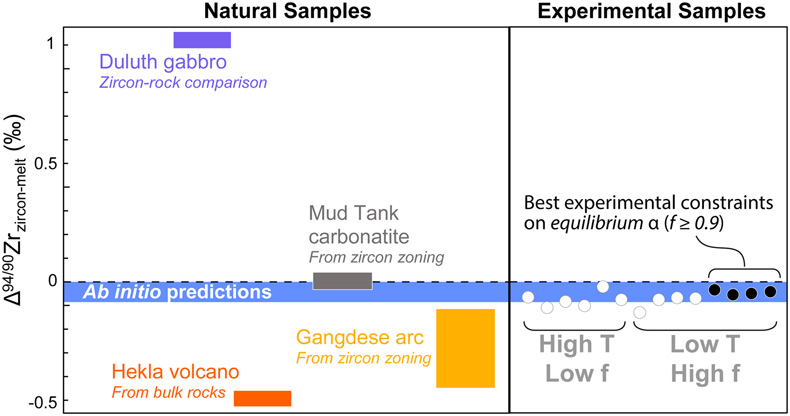
Figure 3 Summary of zircon-melt fractionation factors from ab initio calculations at ≥700 °C (Chen et al., 2020
Chen, X., Wang, W., Zhang, Z., Nie, N.X., and Dauphas, N. (2020) Evidence from Ab Initio and Transport Modeling for Diffusion-Driven Zirconium Isotopic Fractionation in Igneous Rocks. ACS Earth and Space Chemistry 4, 1572–1595. https://doi.org/10.1021/acsearthspacechem.0c00146
; Méheut et al., 2021Méheut, M., Ibañez-Mejia, M., and Tissot, F.L.H. (2021) Drivers of zirconium isotope fractionation in Zr-bearing phases and melts: The roles of vibrational, nuclear field shift and diffusive effects. Geochimica Cosmochimica Acta 292, 217–234. https://doi.org/10.1016/j.gca.2020.09.028
), natural samples (Ibañez-Mejia and Tissot, 2019Ibañez-Mejia, M., and Tissot, F.L.H. (2019) Extreme Zr stable isotope fractionation during magmatic fractional crystallization. Science Advances 5, eaax8648. https://doi.org/10.1126/sciadv.aax8648
; Inglis et al., 2019Inglis, E.C., Moynier, F., Creech, J., Deng, Z., Day, J.M.D., Teng, F.Z., Bizzarro, M., Jackson, M., and Savage, P. (2019) Isotopic fractionation of zirconium during magmatic differentiation and the stable isotope composition of the silicate Earth. Geochimica Cosmochimica Acta 250, 311–323. https://doi.org/10.1016/j.gca.2019.02.010
; Guo et al., 2020Guo, J.L. Wang, Z., Zhang, W., Moynier, F., Cui, D., Hu, Z., Ducea, M. (2020) Significant Zr isotope variations in single zircon grains recording magma evolution history. Proceedings of the National Academy of Sciences 117, 21125–21131. https://doi.org/10.1073/pnas.2002053117
; Tompkins et al., 2020Tompkins, H.G.D., Zieman, L.J., Ibañez-Mejia, M., and Tissot, F.L.H. (2020) Zirconium stable isotope analysis of zircon by MC-ICP-MS: Methods and application to evaluating intra-crystalline zonation in a zircon megacryst. Journal of Analytical Atomic Spectrometry 35, 1167–1186. https://doi.org/10.1039/C9JA00315K
), and experimental samples (this study).