Contribution of the nuclear field shift to kinetic uranium isotope fractionation
Affiliations | Corresponding Author | Cite as | Funding information- Share this article




-
Article views:168Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Figures
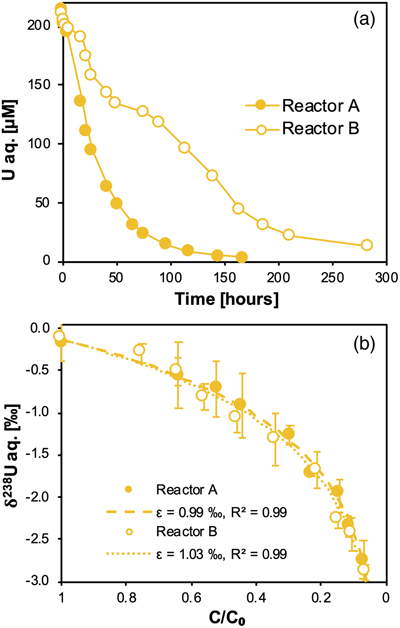 Figure 1 (a) Concentration of aqueous U (representing UVI), as a function of time, in reactors containing 200 μM UVI and 30 mM sodium bicarbonate incubated with S. oneidensis. Filled and open symbols depict duplicate reactors. (b) δ238U values for aqueous U reported as a function of the remaining aqueous U fraction. Filled and open symbols depict duplicate reactors and error bars show 2 standard deviations of the mean of triplicate measurements. Rayleigh model curves for each duplicate reactor are shown in dashed lines, along with their corresponding isotope enrichment factors (ɛ). See Supplementary Information for definition of δ238U. | 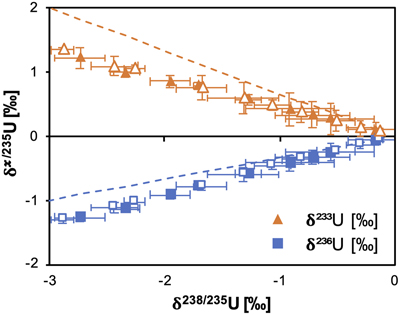 Figure 2 Three-isotope plots for delta values of all samples. Filled and open symbols depict duplicate reactors and error bars show two standard deviations of the mean of triplicate measurements. Dashed lines represent theoretical relationships for mass-dependent fractionation. | 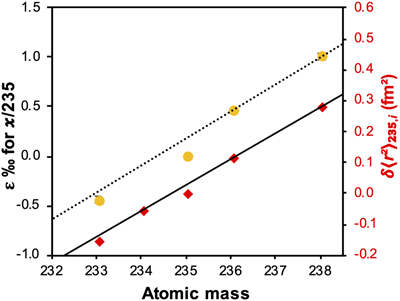 Figure 3 Fractionation factors (ɛ) for each atomic mass. Symbols and error bars depict the mean and standard deviation of duplicate reactors. Where not visible, the error is within the size of the symbol. Mean square nuclear charge radii (δ〈r2〉235,i =δ〈r2〉i − δ〈r2〉235) for each atomic mass were taken from Angeli and Marinova (2013). The lines represent linear regressions of ɛ and δ〈r2〉235,i for even-mass numbers only. | 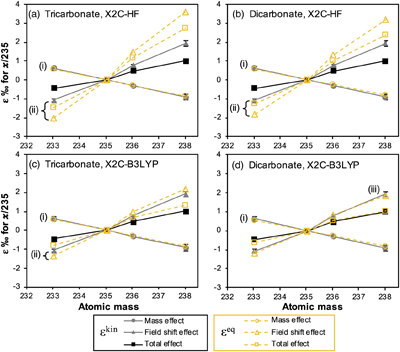 Figure 4 Isotope enrichment factors from the bacterial reduction experiment (ɛkin) and ab initio calculated equilibrium isotope enrichment factors (ɛeq) for the mass effect, the nuclear field shift effect and their sum (total effect) for each atomic mass. Equilibrium calculations were performed for either (a, c) tricarbonate, UO2(CO3)34−, or (b, d) dicarbonate, UO2(CO3)22−, as the UVI species. Calculations of ln Knv for ɛeq were performed using either (a, b) the Hartree-Fock method (X2C-HF) or (c, d) density functional theory (DFT) with the B3LYP functional (X2C-B3LYP). Symbols and error bars depict the mean and standard deviation of values derived from analysis of the data from duplicate reactors. A comparison of experimentally measured ɛ and recalculated total ɛ (after decomposition of the experimental data into the field shift and mass effect terms) is presented in Figure S-6. Trend (i) points to the consistent values obtained for MDF from theory and experiment, (ii) points to the discrepancy between theory and experiment for the NFSE contribution in three of the four cases, and (iii) points to the agreement between NFSE theory and experiment in the case of dicarbonate speciation and DFT calculations. |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
top
Introduction
Redox transformations of uranium (U) lead to measurable fractionation of U isotopes. These fractionations typically result in the enrichment of the heavy isotope (238U) in the reduced state, the opposite direction of the mass-dependent fractionation observed for light elements (Andersen et al., 2017
Andersen, M.B., Stirling, C.H., Weyer, S. (2017) Uranium Isotope Fractionation. Reviews in Mineralogy and Geochemistry 82, 799–850. https://doi.org/10.2138/rmg.2017.82.19
). Further, isotope exchange reactions have revealed anomalous fractionations of the odd-mass isotopes, i.e. 233U and 235U, which deviate from the linear relationship between mass and fractionation magnitude observed for the even-mass isotopes (Fujii et al., 1989aFujii, Y., Nomura, M., Okamoto, M., Onitsuka, H., Kawakami, F., Takeda, K. (1989a) An Anomalous Isotope Effect of 235U in U(IV)-U(VI) Chemical Exchange. Zeitschrift für Naturforschung A 44, 395–398. https://doi.org/10.1515/zna-1989-0507
, 1989bFujii, Y., Nomura, M., Onitsuka, H., Takeda, K. (1989b) Anomalous Isotope Fractionation in Uranium Enrichment Process. Journal of Nuclear Science and Technology 26, 1061–1064. https://doi.org/10.1080/18811248.1989.9734427
; Nomura et al., 1996Nomura, M., Higuchi, N., Fujii, Y. (1996) Mass Dependence of Uranium Isotope Effects in the U(IV)−U(VI) Exchange Reaction. Journal of the American Chemical Society 118, 9127–9130. https://doi.org/10.1021/ja954075s
). This odd-even staggering was observed to correlate with the isotope shifts in the atomic spectra of the isotopes, and specifically with the nuclear field shift, whereby distortions in the sizes and shapes of nuclei (the nuclear volume) between isotopes impact the electron densities surrounding the nucleus, which in turn impact ground state electronic energies. This led to the inclusion of a nuclear field shift (NFS) term in the theoretical calculation of isotopic enrichment factors for heavy elements (Bigeleisen, 1996Bigeleisen, J. (1996) Nuclear Size and Shape Effects in Chemical Reactions. Isotope Chemistry of the Heavy Elements. Journal of the American Chemical Society 118, 3676–3680. https://doi.org/10.1021/ja954076k
).These isotope exchange reactions have been assumed to be equilibrium processes (Fujii et al., 2009
Fujii, T., Moynier, F., Albarède, F. (2009) The nuclear field shift effect in chemical exchange reactions. Chemical Geology 267, 139–156. https://doi.org/10.1016/j.chemgeo.2009.06.015
), and the nuclear field shift effect (NFSE) itself has thus far been calculated only for equilibrium exchange reactions (Bigeleisen, 1996Bigeleisen, J. (1996) Nuclear Size and Shape Effects in Chemical Reactions. Isotope Chemistry of the Heavy Elements. Journal of the American Chemical Society 118, 3676–3680. https://doi.org/10.1021/ja954076k
; Moynier et al., 2013Moynier, F., Fujii, T., Brennecka, G.A., Nielsen, S.G. (2013) Nuclear field shift in natural environments. Comptes Rendus Geoscience 345, 150–159. https://doi.org/10.1016/j.crte.2013.01.004
). Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996Bigeleisen, J. (1996) Nuclear Size and Shape Effects in Chemical Reactions. Isotope Chemistry of the Heavy Elements. Journal of the American Chemical Society 118, 3676–3680. https://doi.org/10.1021/ja954076k
; Schauble, 2007Schauble, E.A. (2007) Role of nuclear volume in driving equilibrium stable isotope fractionation of mercury, thallium, and other very heavy elements. Geochimica et Cosmochimica Acta 71, 2170–2189. https://doi.org/10.1016/j.gca.2007.02.004
; Stirling et al., 2015Stirling, C.H., Andersen, M.B., Warthmann, R., Halliday, A.N. (2015) Isotope fractionation of 238U and 235U during biologically-mediated uranium reduction. Geochimica et Cosmochimica Acta 163, 200–218. https://doi.org/10.1016/j.gca.2015.03.017
), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010Bopp IV, C.J., Lundstrom, C.C., Johnson, T.M., Sandford, R.A., Long, P.E., Williams, K.H. (2010) Uranium 238U/235U Isotope Ratios as Indicators of Reduction: Results from an in situ Biostimulation Experiment at Rifle, Colorado, U.S.A. Environmental Science & Technology 44, 5927–5933. https://doi.org/10.1021/es100643v
; Basu et al., 2014Basu, A., Sanford, R.A., Johnson, T.M., Lundstrom, C.C., Löffler, F.E. (2014) Uranium isotopic fractionation factors during U(VI) reduction by bacterial isolates. Geochimica et Cosmochimica Acta 136, 100–113. https://doi.org/10.1016/j.gca.2014.02.041
, 2020Basu, A., Wanner, C., Johnson, T.M., Lundstrom, C.C., Sanford, R.A., Sonnenthal, E.L., Boyanov, M.I., Kemner, K.M. (2020) Microbial U Isotope Fractionation Depends on the U(VI) Reduction Rate. Environmental Science & Technology 54, 2295–2303. https://doi.org/10.1021/acs.est.9b05935
; Stirling et al., 2015Stirling, C.H., Andersen, M.B., Warthmann, R., Halliday, A.N. (2015) Isotope fractionation of 238U and 235U during biologically-mediated uranium reduction. Geochimica et Cosmochimica Acta 163, 200–218. https://doi.org/10.1016/j.gca.2015.03.017
). However, no direct evidence for the NFSE during kinetic U reduction has been provided to date; i.e. the odd-even staggering in the fractionation of isotopes has not yet been observed.Whilst the NFSE has been observed during abiotic and kinetic fractionations of Hg isotopes (Zheng and Hintelmann, 2010
Zheng, W., Hintelmann, H. (2010) Nuclear Field Shift Effect in Isotope Fractionation of Mercury during Abiotic Reduction in the Absence of Light. The Journal of Physical Chemistry A 114, 4238–4245. https://doi.org/10.1021/jp910353y
), to our knowledge, there is no evidence of the NFSE during the biotic fractionation of any element. Indeed, mass-independent isotope fractionation of Hg has been observed in biological systems (e.g., in fish) but this has been attributed to the nuclear spin effects or photochemical reactions, rather than to the NFSE (Kritee et al., 2009Kritee, K., Barkay, T., Blum, J.D. (2009) Mass dependent stable isotope fractionation of mercury during mer mediated microbial degradation of monomethylmercury. Geochimica et Cosmochimica Acta 73, 1285–1296. https://doi.org/10.1016/j.gca.2008.11.038
; Epov et al., 2011Epov, V.N., Malinovskiy, D., Vanhaecke, F., Bégué, D., Donard, O.F.X. (2011) Modern mass spectrometry for studying mass-independent fractionation of heavy stable isotopes in environmental and biological sciences. Journal of Analytical Atomic Spectrometry 26, 1142–1156. https://doi.org/10.1039/c0ja00231c
).top
Results
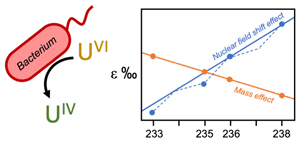
Here, we provide direct evidence of the NFSE during kinetic isotope fractionation via the enzymatic reduction of UVI by the bacterium, Shewanella oneidensis strain MR-1. To achieve this result, we measured the simultaneous fractionation of 233U, 235U, 236U and 238U throughout this reaction and report the odd-even staggering trend only previously seen during abiotic chemical exchange reactions.
First, we prepared an isotope mix of the IRMM-184 natural U standard and the IRMM-3636 233U and 236U “double spike”, typically used to correct for instrumental mass bias during MC-ICP-MS (multi-collector inductively coupled plasma mass spectrometry) analyses of the 238U/235U ratio. The isotope mix was supplied to anoxic reactors containing S. oneidensis MR-1 in the presence of lactate, which serves as the electron donor for UVI reduction, and 30 mM sodium bicarbonate, which complexes the UVI to give aqueous tri- and dicarbonate species (Fig. S-1). This well documented reaction leads to the reductive precipitation of solid phase UIV through the extracellular transfer of electrons via enzymes on the bacterial surface (Wall and Krumholz, 2006
Wall, J.D., Krumholz, L.R. (2006) Uranium Reduction. Annual Review of Microbiology 60, 149–166. https://doi.org/10.1146/annurev.micro.59.030804.121357
).Here, we show that for duplicate systems, aqueous U concentrations decreased over several days, indicative of the precipitation of UIV (Fig. 1a). This reaction was accompanied by the fractionation of 238U and 235U, such that the light 235U was enriched in the residual unreacted aqueous UVI, as evidenced by the progressively negative δ238U values (Fig. 1b). This fractionation is well described by Rayleigh distillation models, from which the derived fractionation factors (ɛ) are ∼1 ‰. These values are very typical for these biologically mediated reactions and demonstrate the sequestration of the isotopically heavy UIV product from the reactants, as shown previously for U isotope fractionation (Basu et al., 2014
Basu, A., Sanford, R.A., Johnson, T.M., Lundstrom, C.C., Löffler, F.E. (2014) Uranium isotopic fractionation factors during U(VI) reduction by bacterial isolates. Geochimica et Cosmochimica Acta 136, 100–113. https://doi.org/10.1016/j.gca.2014.02.041
; Stirling et al., 2015Stirling, C.H., Andersen, M.B., Warthmann, R., Halliday, A.N. (2015) Isotope fractionation of 238U and 235U during biologically-mediated uranium reduction. Geochimica et Cosmochimica Acta 163, 200–218. https://doi.org/10.1016/j.gca.2015.03.017
; Stylo et al., 2015Stylo, M., Neubert, N., Wang, Y., Monga, N., Romaniello, S.J., Weyer, S., Bernier-Latmani, R. (2015) Uranium isotopes fingerprint biotic reduction. Proceedings of the National Academy of Sciences 112, 5619–5624. https://doi.org/10.1073/pnas.1421841112
).
Figure 1 (a) Concentration of aqueous U (representing UVI), as a function of time, in reactors containing 200 μM UVI and 30 mM sodium bicarbonate incubated with S. oneidensis. Filled and open symbols depict duplicate reactors. (b) δ238U values for aqueous U reported as a function of the remaining aqueous U fraction. Filled and open symbols depict duplicate reactors and error bars show 2 standard deviations of the mean of triplicate measurements. Rayleigh model curves for each duplicate reactor are shown in dashed lines, along with their corresponding isotope enrichment factors (ɛ). See Supplementary Information for definition of δ238U.
The inclusion of 233U and 236U in the isotope mix allowed the fractionation of these additional odd- and even-mass isotopes to be monitored (Fig. S-2), in order to reveal the presence of the odd-even staggering that would implicate the role of the NFSE in the fractionation of U isotopes. Here, three-isotope plots revealed that the fractionation behaviour did not conform to the theoretical relationship for mass-dependent isotope fractionation (Figs. 2, S-3). Total fractionation between 236U and 235U was larger than expected for a mass difference of 1 amu, compared to the fractionation of 238U and 235U (Δm = 3 amu). Additionally, the fractionation between the two odd-isotopes, 233U and 235U (Δm = 2 amu) was less than expected compared to the fractionation of 238U and 235U. These anomalous fractionations are consistent with those observed previously for U isotopes in chemical exchange reactions, in which fractionation factors for each isotope scale better with the mean square nuclear charge radii rather than the isotope mass (Fig. S-4), indicating that the nuclear volume dominates the fractionation (Fujii et al., 2009
Fujii, T., Moynier, F., Albarède, F. (2009) The nuclear field shift effect in chemical exchange reactions. Chemical Geology 267, 139–156. https://doi.org/10.1016/j.chemgeo.2009.06.015
; Moynier et al., 2013Moynier, F., Fujii, T., Brennecka, G.A., Nielsen, S.G. (2013) Nuclear field shift in natural environments. Comptes Rendus Geoscience 345, 150–159. https://doi.org/10.1016/j.crte.2013.01.004
). Here, we also observe odd-even isotope staggering in the relationship between isotopic mass and fractionation factors and demonstrate this same trend between ɛ and the mean square nuclear charge radii (Fig. 3) (Angeli and Marinova, 2013Angeli, I., Marinova, K.P. (2013) Table of experimental nuclear ground state charge radii: An update. Atomic Data and Nuclear Data Tables 99, 69–95. https://doi.org/10.1016/j.adt.2011.12.006
). Thus, in addition to the direction of U isotope fractionation, these data offer strong evidence that the NFSE is also responsible for the mass-independent nature of isotope fractionation observed for this kinetic reaction.
Figure 2 Three-isotope plots for delta values of all samples. Filled and open symbols depict duplicate reactors and error bars show two standard deviations of the mean of triplicate measurements. Dashed lines represent theoretical relationships for mass-dependent fractionation.

Figure 3 Fractionation factors (ɛ) for each atomic mass. Symbols and error bars depict the mean and standard deviation of duplicate reactors. Where not visible, the error is within the size of the symbol. Mean square nuclear charge radii (δ〈r2〉235,i =δ〈r2〉i − δ〈r2〉235) for each atomic mass were taken from Angeli and Marinova (2013)
Angeli, I., Marinova, K.P. (2013) Table of experimental nuclear ground state charge radii: An update. Atomic Data and Nuclear Data Tables 99, 69–95. https://doi.org/10.1016/j.adt.2011.12.006
. The lines represent linear regressions of ɛ and δ〈r2〉235,i for even-mass numbers only.To probe whether the observed mass-independent fractionation arose from ongoing abiotic equilibrium isotope exchange between reactant UVI and the solid UIV product, or from the kinetically controlled enzymatic reduction, we performed isotope exchange experiments between isotopically heavy aqueous UVI carbonate (initial δ238U = ∼5 ‰) and the UIV products of the bioreduction experiment (initial δ238U = 0 ‰). Here, we controlled the U speciation to be the same as during bioreduction using the same solution composition and ensured no further biologically mediated redox change by inactivating bacterial cells via sonication. Over several months, we observed the progressive depletion of the heavy 238U from aqueous UVI (Fig. S-5) as it became enriched in the UIV species, as expected. However, this process was minor and theoretical equilibrium was not achieved (e.g., ɛeq = 1.1 to 2.7 ‰ from ab initio calculation; Table S-1). That is to say, the aqueous UVI remained isotopically heavier than the UIV solid phase after several months, compared with the few days required to generate isotopically heavy UIV during bioreduction. Additionally, the slight increase in aqueous U suggests that at least part of the decrease in δ238Uaq may have actually been due to release of light U from the solid, rather than isotope exchange between dissolved and solid phases. These observations suggest that, whilst ongoing equilibrium isotope exchange may make a minor contribution to the observed direction of the fractionation (enrichment of the heavy isotope in the UIV product, as demonstrated by Wang et al., 2015
Wang, X., Johnson, T.M., Lundstrom, C.C. (2015) Low temperature equilibrium isotope fractionation and isotope exchange kinetics between U(IV) and U(VI). Geochimica et Cosmochimica Acta 158, 262–275. https://doi.org/10.1016/j.gca.2015.03.006
), it does not account for the magnitude of isotope fractionation during the kinetic reaction of biological reduction.To calculate the contribution of the NFSE and the mass effect to the fractionation factors obtained for each isotope during the enzymatic reduction, we used the methods of Fujii et al. (2009)
Fujii, T., Moynier, F., Albarède, F. (2009) The nuclear field shift effect in chemical exchange reactions. Chemical Geology 267, 139–156. https://doi.org/10.1016/j.chemgeo.2009.06.015
and Moynier et al. (2009)Moynier, F., Fujii, T., Telouk, P. (2009) Mass-independent isotopic fractionation of tin in chemical exchange reaction using a crown ether. Analytica Chimica Acta 632, 234–239. https://doi.org/10.1016/j.aca.2008.11.015
to obtain the scaling factors of the conventional mass effect and the nuclear field shift term that appear in Bigeleisen’s (1996)Bigeleisen, J. (1996) Nuclear Size and Shape Effects in Chemical Reactions. Isotope Chemistry of the Heavy Elements. Journal of the American Chemical Society 118, 3676–3680. https://doi.org/10.1021/ja954076k
theory (Figs. 4, S-6). Whilst this analysis was developed initially for isotopic equilibrium conditions, it succeeds in reproducing the odd-even staggering trend (highlighted by the regression of the even isotopes in Fig. S-6) and suggests the dominant contribution of the NFSE to the overall observed kinetic fractionation factors.
Figure 4 Isotope enrichment factors from the bacterial reduction experiment (ɛkin) and ab initio calculated equilibrium isotope enrichment factors (ɛeq) for the mass effect, the nuclear field shift effect and their sum (total effect) for each atomic mass. Equilibrium calculations were performed for either (a, c) tricarbonate, UO2(CO3)34−, or (b, d) dicarbonate, UO2(CO3)22−, as the UVI species. Calculations of ln Knv for ɛeq were performed using either (a, b) the Hartree-Fock method (X2C-HF) or (c, d) density functional theory (DFT) with the B3LYP functional (X2C-B3LYP). Symbols and error bars depict the mean and standard deviation of values derived from analysis of the data from duplicate reactors. A comparison of experimentally measured ɛ and recalculated total ɛ (after decomposition of the experimental data into the field shift and mass effect terms) is presented in Figure S-6. Trend (i) points to the consistent values obtained for MDF from theory and experiment, (ii) points to the discrepancy between theory and experiment for the NFSE contribution in three of the four cases, and (iii) points to the agreement between NFSE theory and experiment in the case of dicarbonate speciation and DFT calculations.
Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006
Fujii, Y., Higuchi, N., Haruno, Y., Nomura, M., Suzuki, T. (2006) Temperature Dependence of Isotope Effects in Uranium Chemical Exchange Reactions. Journal of Nuclear Science and Technology 43, 400–406. https://doi.org/10.1080/18811248.2006.9711111
; Abe et al., 2008Abe, M., Suzuki, T., Fujii, Y., Hada, M., Hirao, K. (2008) An ab initio molecular orbital study of the nuclear volume effects in uranium isotope fractionations. The Journal of Chemical Physics 129, 164309. https://doi.org/10.1063/1.2992616
, 2010Abe, M., Suzuki, T., Fujii, Y., Hada, M., Hirao, K. (2010) Ligand effect on uranium isotope fractionations caused by nuclear volume effects: An ab initio relativistic molecular orbital study. The Journal of Chemical Physics 133, 044309. https://doi.org/10.1063/1.3463797
; Basu et al., 2014Basu, A., Sanford, R.A., Johnson, T.M., Lundstrom, C.C., Löffler, F.E. (2014) Uranium isotopic fractionation factors during U(VI) reduction by bacterial isolates. Geochimica et Cosmochimica Acta 136, 100–113. https://doi.org/10.1016/j.gca.2014.02.041
; Wang et al., 2015Wang, X., Johnson, T.M., Lundstrom, C.C. (2015) Low temperature equilibrium isotope fractionation and isotope exchange kinetics between U(IV) and U(VI). Geochimica et Cosmochimica Acta 158, 262–275. https://doi.org/10.1016/j.gca.2015.03.006
; Stirling et al., 2015Stirling, C.H., Andersen, M.B., Warthmann, R., Halliday, A.N. (2015) Isotope fractionation of 238U and 235U during biologically-mediated uranium reduction. Geochimica et Cosmochimica Acta 163, 200–218. https://doi.org/10.1016/j.gca.2015.03.017
; Stylo et al., 2015Stylo, M., Neubert, N., Wang, Y., Monga, N., Romaniello, S.J., Weyer, S., Bernier-Latmani, R. (2015) Uranium isotopes fingerprint biotic reduction. Proceedings of the National Academy of Sciences 112, 5619–5624. https://doi.org/10.1073/pnas.1421841112
; Andersen et al., 2017Andersen, M.B., Stirling, C.H., Weyer, S. (2017) Uranium Isotope Fractionation. Reviews in Mineralogy and Geochemistry 82, 799–850. https://doi.org/10.2138/rmg.2017.82.19
; Brown et al., 2018Brown, S.T., Basu, A., Ding, X., Christensen, J.N., DePaolo, D.J. (2018) Uranium isotope fractionation by abiotic reductive precipitation. Proceedings of the National Academy of Sciences 115, 8688–8693. https://doi.org/10.1073/pnas.1805234115
; Sato et al., 2021Sato, A., Bernier-Latmani, R., Hada, M., Abe, M. (2021) Ab initio and steady-state models for uranium isotope fractionation in multi-step biotic and abiotic reduction. Geochimica et Cosmochimica Acta 307, 212–227. https://doi.org/10.1016/j.gca.2021.05.044
; Li and Tissot, 2023Li, H., Tissot, F.L.H. (2023) UID: The uranium isotope database. Chemical Geology 618, 121221. https://doi.org/10.1016/j.chemgeo.2022.121221
). However, the extent to which the relative contributions of the mass effect and the NFSE lead to this discrepancy has not been explored. This is of fundamental importance to the understanding of how isotope fractionation observed during kinetic reactions relates to that calculated for isotopic equilibrium. Thus, we compared the magnitudes of the decomposed mass and field shift effects from the experimental kinetic reaction (ɛkin), to the mass and field shift effect contributions determined for full equilibrium fractionation via ab initio calculations (ɛeq) (Fig. 4). This comparison reveals that the contribution of the mass effect to ɛkin approximates that predicted for equilibrium, no matter whether the tri- or dicarbonate UVI species is assumed to be preferentially reduced by the bacterium (Fig. 4; trend (i)). On the other hand, the analysis indicates that the contribution of the NFSE to ɛkin is typically much smaller than that for ɛeq, but varies depending on the calculation method (density functional theory (DFT) versus Hartree-Fock (HF)) and the UVI species used (Fig. 4a–c; trend (ii)). Indeed, calculations using DFT and the dicarbonate UVI species appear to suggest that the isotope fractionation of the kinetic reaction approaches full equilibrium (Fig. 4d; trend (iii)). However, previous calculations using the HF method showed better agreement with the experimental ɛeq for the UVI/UIV-chloride isotope exchange reaction compared with DFT calculations, suggesting that the results of the HF method may be more accurate (Wang et al., 2015Wang, X., Johnson, T.M., Lundstrom, C.C. (2015) Low temperature equilibrium isotope fractionation and isotope exchange kinetics between U(IV) and U(VI). Geochimica et Cosmochimica Acta 158, 262–275. https://doi.org/10.1016/j.gca.2015.03.006
; Sato et al., 2021Sato, A., Bernier-Latmani, R., Hada, M., Abe, M. (2021) Ab initio and steady-state models for uranium isotope fractionation in multi-step biotic and abiotic reduction. Geochimica et Cosmochimica Acta 307, 212–227. https://doi.org/10.1016/j.gca.2021.05.044
). Whilst ab initio calculations of ɛeq are not easy to verify due to a lack of experimental data with which to validate them, these data suggest that the mass effect has reached equilibrium, whilst the NFSE has not. This raises the question of how these two effects are manifested during kinetic reactions and what controls their relative expressions.A recent study by Brown et al. (2018)
Brown, S.T., Basu, A., Ding, X., Christensen, J.N., DePaolo, D.J. (2018) Uranium isotope fractionation by abiotic reductive precipitation. Proceedings of the National Academy of Sciences 115, 8688–8693. https://doi.org/10.1073/pnas.1805234115
explored the effect of abiotic UVI reduction rates, controlled by U speciation, on attendant U isotope fractionation. To explain the inverse reaction rate-fractionation relationship, a model was developed incorporating a variable contribution of the NFSE that was dependent on the ratio of forward to backward reactions, but that also required isotopic exchange between UVI and UIV. However, in our study we observed only a minor contribution from equilibrium isotope exchange that cannot explain the magnitude of isotope fractionation during the kinetic reaction and this suggests that kinetic fractionation may also include the NFSE.The mathematical basis for the inclusion of NFSE in kinetic fractionation has been derived by Sato et al. (2021)
Sato, A., Bernier-Latmani, R., Hada, M., Abe, M. (2021) Ab initio and steady-state models for uranium isotope fractionation in multi-step biotic and abiotic reduction. Geochimica et Cosmochimica Acta 307, 212–227. https://doi.org/10.1016/j.gca.2021.05.044
. The authors introduced a model of kinetic uranium isotope fractionation that incorporates transition state theory to allow the inclusion of the NFSE within a multi-step UVI reduction reaction, independent of subsequent equilibrium isotope exchange between the oxidised and reduced U. The model was then employed to re-interpret the data of Brown et al. (2018)Brown, S.T., Basu, A., Ding, X., Christensen, J.N., DePaolo, D.J. (2018) Uranium isotope fractionation by abiotic reductive precipitation. Proceedings of the National Academy of Sciences 115, 8688–8693. https://doi.org/10.1073/pnas.1805234115
, demonstrating that the observations can arise from kinetic fractionation components that include the NFSE, without the requirement for independent equilibrium isotope exchange between the initial reactant and the final product. Rather, the model indicates that the magnitude of NFSE expression is dependent on the degree of reverse electron transfer (back reaction). This has since been confirmed experimentally using purified UVI reducing proteins of various redox states. Fully reduced proteins facilitated rapid electron transfer with limited back reaction and little isotopic fractionation, whereas partially reduced proteins permitted significant NFSE-dominated fractionation linked to the allowance for extensive reverse electron transfer (Brown et al., 2023Brown, A.R., Molinas, M., Roebbert, Y., Sato, A., Abe, M., Weyer, S., Bernier-Latmani, R. (2023) Electron flux is a key determinant of uranium isotope fractionation during bacterial reduction. Communications Earth & Environment 4, 329. https://doi.org/10.1038/s43247-023-00989-x
).Our data support the view that the mass effect is both an equilibrium and kinetic isotope fractionation, in which the full fractionation at equilibrium can be expressed during kinetically controlled reactions. On the other hand, the NFSE may be exclusively an equilibrium fractionation between the instantaneous products and transition state(s), and the transition state(s) and the reactants, and as such, its expression during kinetic fractionation within the reduction reaction may be dependent on reaction reversibility (Fujii et al., 2009
Fujii, T., Moynier, F., Albarède, F. (2009) The nuclear field shift effect in chemical exchange reactions. Chemical Geology 267, 139–156. https://doi.org/10.1016/j.chemgeo.2009.06.015
; Moynier et al., 2013Moynier, F., Fujii, T., Brennecka, G.A., Nielsen, S.G. (2013) Nuclear field shift in natural environments. Comptes Rendus Geoscience 345, 150–159. https://doi.org/10.1016/j.crte.2013.01.004
; Yang and Liu, 2016Yang, S., Liu, Y. (2016) Nuclear field shift effects on stable isotope fractionation: a review. Acta Geochimica 35, 227–239. https://doi.org/10.1007/s11631-016-0109-3
; Sato et al., 2021Sato, A., Bernier-Latmani, R., Hada, M., Abe, M. (2021) Ab initio and steady-state models for uranium isotope fractionation in multi-step biotic and abiotic reduction. Geochimica et Cosmochimica Acta 307, 212–227. https://doi.org/10.1016/j.gca.2021.05.044
). This would explain the range of fractionation factors observed in the laboratory and nature, including both mass-dependent and mass-independent directions of fractionation.Further work is required to explore the factors that control the relative contributions of the two effects during kinetic isotope fractionations and rule out the contribution of other isotope effects, e.g., a nuclear spin effect or magnetic isotope effect (Epov et al., 2011
Epov, V.N., Malinovskiy, D., Vanhaecke, F., Bégué, D., Donard, O.F.X. (2011) Modern mass spectrometry for studying mass-independent fractionation of heavy stable isotopes in environmental and biological sciences. Journal of Analytical Atomic Spectrometry 26, 1142–1156. https://doi.org/10.1039/c0ja00231c
). Indeed, different reaction mechanisms of Hg reduction, e.g., photoreduction versus reduction by dissolved organic matter or SnCl2, resulted in different relative contributions of mass-dependent and mass-independent fractionation (Bergquist and Blum, 2007Bergquist, B.A., Blum, J.D. (2007) Mass-Dependent and -Independent Fractionation of Hg Isotopes by Photoreduction in Aquatic Systems. Science 318, 417–420. https://doi.org/10.1126/science.1148050
; Zheng and Hintelmann, 2010Zheng, W., Hintelmann, H. (2010) Nuclear Field Shift Effect in Isotope Fractionation of Mercury during Abiotic Reduction in the Absence of Light. The Journal of Physical Chemistry A 114, 4238–4245. https://doi.org/10.1021/jp910353y
).Collectively, the data presented here show unambiguous evidence for the contribution of the nuclear field shift to isotope fractionation during kinetic U reduction and confirm that previously observed fractionations (reporting enrichment of the heavy isotope in the product) arise from the dominance of the nuclear field shift effect.
top
Acknowledgements
Funding for this work was provided by an ERC consolidator grant awarded to RB-L (
Editor: Claudine Stirling
top
References
Abe, M., Suzuki, T., Fujii, Y., Hada, M., Hirao, K. (2008) An ab initio molecular orbital study of the nuclear volume effects in uranium isotope fractionations. The Journal of Chemical Physics 129, 164309. https://doi.org/10.1063/1.2992616
 Show in context
Show in context Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Abe, M., Suzuki, T., Fujii, Y., Hada, M., Hirao, K. (2010) Ligand effect on uranium isotope fractionations caused by nuclear volume effects: An ab initio relativistic molecular orbital study. The Journal of Chemical Physics 133, 044309. https://doi.org/10.1063/1.3463797
 Show in context
Show in context Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Andersen, M.B., Stirling, C.H., Weyer, S. (2017) Uranium Isotope Fractionation. Reviews in Mineralogy and Geochemistry 82, 799–850. https://doi.org/10.2138/rmg.2017.82.19
 Show in context
Show in context Redox transformations of uranium (U) lead to measurable fractionation of U isotopes. These fractionations typically result in the enrichment of the heavy isotope (238U) in the reduced state, the opposite direction of the mass-dependent fractionation observed for light elements (Andersen et al., 2017).
View in article
Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Angeli, I., Marinova, K.P. (2013) Table of experimental nuclear ground state charge radii: An update. Atomic Data and Nuclear Data Tables 99, 69–95. https://doi.org/10.1016/j.adt.2011.12.006
 Show in context
Show in context Here, we also observe odd-even isotope staggering in the relationship between isotopic mass and fractionation factors and demonstrate this same trend between ɛ and the mean square nuclear charge radii (Fig. 3) (Angeli and Marinova, 2013).
View in article
Fractionation factors (ɛ) for each atomic mass. Symbols and error bars depict the mean and standard deviation of duplicate reactors. Where not visible, the error is within the size of the symbol. Mean square nuclear charge radii (δ〈r2〉235,i =δ〈r2〉i − δ〈r2〉235) for each atomic mass were taken from Angeli and Marinova (2013).
View in article
Basu, A., Sanford, R.A., Johnson, T.M., Lundstrom, C.C., Löffler, F.E. (2014) Uranium isotopic fractionation factors during U(VI) reduction by bacterial isolates. Geochimica et Cosmochimica Acta 136, 100–113. https://doi.org/10.1016/j.gca.2014.02.041
 Show in context
Show in context Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996; Schauble, 2007; Stirling et al., 2015), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010; Basu et al., 2014, 2020; Stirling et al., 2015).
View in article
These values are very typical for these biologically mediated reactions and demonstrate the sequestration of the isotopically heavy UIV product from the reactants, as shown previously for U isotope fractionation (Basu et al., 2014; Stirling et al., 2015; Stylo et al., 2015).
View in article
Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Basu, A., Wanner, C., Johnson, T.M., Lundstrom, C.C., Sanford, R.A., Sonnenthal, E.L., Boyanov, M.I., Kemner, K.M. (2020) Microbial U Isotope Fractionation Depends on the U(VI) Reduction Rate. Environmental Science & Technology 54, 2295–2303. https://doi.org/10.1021/acs.est.9b05935
 Show in context
Show in context Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996; Schauble, 2007; Stirling et al., 2015), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010; Basu et al., 2014, 2020; Stirling et al., 2015).
View in article
Bergquist, B.A., Blum, J.D. (2007) Mass-Dependent and -Independent Fractionation of Hg Isotopes by Photoreduction in Aquatic Systems. Science 318, 417–420. https://doi.org/10.1126/science.1148050
 Show in context
Show in context Further work is required to explore the factors that control the relative contributions of the two effects during kinetic isotope fractionations and rule out the contribution of other isotope effects, e.g., a nuclear spin effect or magnetic isotope effect (Epov et al., 2011). Indeed, different reaction mechanisms of Hg reduction, e.g., photoreduction versus reduction by dissolved organic matter or SnCl2, resulted in different relative contributions of mass-dependent and mass-independent fractionation (Bergquist and Blum, 2007; Zheng and Hintelmann, 2010).
View in article
Bigeleisen, J. (1996) Nuclear Size and Shape Effects in Chemical Reactions. Isotope Chemistry of the Heavy Elements. Journal of the American Chemical Society 118, 3676–3680. https://doi.org/10.1021/ja954076k
 Show in context
Show in context This led to the inclusion of a nuclear field shift (NFS) term in the theoretical calculation of isotopic enrichment factors for heavy elements (Bigeleisen, 1996).
View in article
These isotope exchange reactions have been assumed to be equilibrium processes (Fujii et al., 2009), and the nuclear field shift effect (NFSE) itself has thus far been calculated only for equilibrium exchange reactions (Bigeleisen, 1996; Moynier et al., 2013).
View in article
Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996; Schauble, 2007; Stirling et al., 2015), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010; Basu et al., 2014, 2020; Stirling et al., 2015).
View in article
To calculate the contribution of the NFSE and the mass effect to the fractionation factors obtained for each isotope during the enzymatic reduction, we used the methods of Fujii et al. (2009) and Moynier et al. (2009) to obtain the scaling factors of the conventional mass effect and the nuclear field shift term that appear in Bigeleisen’s (1996) theory (Figs. 4, S-6).
View in article
Bopp IV, C.J., Lundstrom, C.C., Johnson, T.M., Sandford, R.A., Long, P.E., Williams, K.H. (2010) Uranium 238U/235U Isotope Ratios as Indicators of Reduction: Results from an in situ Biostimulation Experiment at Rifle, Colorado, U.S.A. Environmental Science & Technology 44, 5927–5933. https://doi.org/10.1021/es100643v
 Show in context
Show in context Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996; Schauble, 2007; Stirling et al., 2015), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010; Basu et al., 2014, 2020; Stirling et al., 2015).
View in article
Brown, A.R., Molinas, M., Roebbert, Y., Sato, A., Abe, M., Weyer, S., Bernier-Latmani, R. (2023) Electron flux is a key determinant of uranium isotope fractionation during bacterial reduction. Communications Earth & Environment 4, 329. https://doi.org/10.1038/s43247-023-00989-x
 Show in context
Show in context Fully reduced proteins facilitated rapid electron transfer with limited back reaction and little isotopic fractionation, whereas partially reduced proteins permitted significant NFSE-dominated fractionation linked to the allowance for extensive reverse electron transfer (Brown et al., 2023).
View in article
Brown, S.T., Basu, A., Ding, X., Christensen, J.N., DePaolo, D.J. (2018) Uranium isotope fractionation by abiotic reductive precipitation. Proceedings of the National Academy of Sciences 115, 8688–8693. https://doi.org/10.1073/pnas.1805234115
 Show in context
Show in context Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
A recent study by Brown et al. (2018) explored the effect of abiotic UVI reduction rates, controlled by U speciation, on attendant U isotope fractionation.
View in article
The model was then employed to re-interpret the data of Brown et al. (2018), demonstrating that the observations can arise from kinetic fractionation components that include the NFSE, without the requirement for independent equilibrium isotope exchange between the initial reactant and the final product.
View in article
Epov, V.N., Malinovskiy, D., Vanhaecke, F., Bégué, D., Donard, O.F.X. (2011) Modern mass spectrometry for studying mass-independent fractionation of heavy stable isotopes in environmental and biological sciences. Journal of Analytical Atomic Spectrometry 26, 1142–1156. https://doi.org/10.1039/c0ja00231c
 Show in context
Show in context Further work is required to explore the factors that control the relative contributions of the two effects during kinetic isotope fractionations and rule out the contribution of other isotope effects, e.g., a nuclear spin effect or magnetic isotope effect (Epov et al., 2011). Indeed, different reaction mechanisms of Hg reduction, e.g., photoreduction versus reduction by dissolved organic matter or SnCl2, resulted in different relative contributions of mass-dependent and mass-independent fractionation (Bergquist and Blum, 2007; Zheng and Hintelmann, 2010).
View in article
Indeed, mass-independent isotope fractionation of Hg has been observed in biological systems (e.g., in fish) but this has been attributed to the nuclear spin effects or photochemical reactions, rather than to the NFSE (Kritee et al., 2009; Epov et al., 2011).
View in article
Fujii, T., Moynier, F., Albarède, F. (2009) The nuclear field shift effect in chemical exchange reactions. Chemical Geology 267, 139–156. https://doi.org/10.1016/j.chemgeo.2009.06.015
 Show in context
Show in context These isotope exchange reactions have been assumed to be equilibrium processes (Fujii et al., 2009), and the nuclear field shift effect (NFSE) itself has thus far been calculated only for equilibrium exchange reactions (Bigeleisen, 1996; Moynier et al., 2013).
View in article
These anomalous fractionations are consistent with those observed previously for U isotopes in chemical exchange reactions, in which fractionation factors for each isotope scale better with the mean square nuclear charge radii rather than the isotope mass (Fig. S-4), indicating that the nuclear volume dominates the fractionation (Fujii et al., 2009; Moynier et al., 2013).
View in article
To calculate the contribution of the NFSE and the mass effect to the fractionation factors obtained for each isotope during the enzymatic reduction, we used the methods of Fujii et al. (2009) and Moynier et al. (2009) to obtain the scaling factors of the conventional mass effect and the nuclear field shift term that appear in Bigeleisen’s (1996) theory (Figs. 4, S-6).
View in article
On the other hand, the NFSE may be exclusively an equilibrium fractionation between the instantaneous products and transition state(s), and the transition state(s) and the reactants, and as such, its expression during kinetic fractionation within the reduction reaction may be dependent on reaction reversibility (Fujii et al., 2009; Moynier et al., 2013; Yang and Liu, 2016; Sato et al., 2021).
View in article
Fujii, Y., Nomura, M., Okamoto, M., Onitsuka, H., Kawakami, F., Takeda, K. (1989a) An Anomalous Isotope Effect of 235U in U(IV)-U(VI) Chemical Exchange. Zeitschrift für Naturforschung A 44, 395–398. https://doi.org/10.1515/zna-1989-0507
 Show in context
Show in context Further, isotope exchange reactions have revealed anomalous fractionations of the odd-mass isotopes, i.e. 233U and 235U, which deviate from the linear relationship between mass and fractionation magnitude observed for the even-mass isotopes (Fujii et al., 1989a, 1989b; Nomura et al., 1996).
View in article
Fujii, Y., Nomura, M., Onitsuka, H., Takeda, K. (1989b) Anomalous Isotope Fractionation in Uranium Enrichment Process. Journal of Nuclear Science and Technology 26, 1061–1064. https://doi.org/10.1080/18811248.1989.9734427
 Show in context
Show in context Further, isotope exchange reactions have revealed anomalous fractionations of the odd-mass isotopes, i.e. 233U and 235U, which deviate from the linear relationship between mass and fractionation magnitude observed for the even-mass isotopes (Fujii et al., 1989a, 1989b; Nomura et al., 1996).
View in article
Fujii, Y., Higuchi, N., Haruno, Y., Nomura, M., Suzuki, T. (2006) Temperature Dependence of Isotope Effects in Uranium Chemical Exchange Reactions. Journal of Nuclear Science and Technology 43, 400–406. https://doi.org/10.1080/18811248.2006.9711111
 Show in context
Show in context Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Kritee, K., Barkay, T., Blum, J.D. (2009) Mass dependent stable isotope fractionation of mercury during mer mediated microbial degradation of monomethylmercury. Geochimica et Cosmochimica Acta 73, 1285–1296. https://doi.org/10.1016/j.gca.2008.11.038
 Show in context
Show in context Indeed, mass-independent isotope fractionation of Hg has been observed in biological systems (e.g., in fish) but this has been attributed to the nuclear spin effects or photochemical reactions, rather than to the NFSE (Kritee et al., 2009; Epov et al., 2011).
View in article
Li, H., Tissot, F.L.H. (2023) UID: The uranium isotope database. Chemical Geology 618, 121221. https://doi.org/10.1016/j.chemgeo.2022.121221
 Show in context
Show in context Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Moynier, F., Fujii, T., Telouk, P. (2009) Mass-independent isotopic fractionation of tin in chemical exchange reaction using a crown ether. Analytica Chimica Acta 632, 234–239. https://doi.org/10.1016/j.aca.2008.11.015
 Show in context
Show in context To calculate the contribution of the NFSE and the mass effect to the fractionation factors obtained for each isotope during the enzymatic reduction, we used the methods of Fujii et al. (2009) and Moynier et al. (2009) to obtain the scaling factors of the conventional mass effect and the nuclear field shift term that appear in Bigeleisen’s (1996) theory (Figs. 4, S-6).
View in article
Moynier, F., Fujii, T., Brennecka, G.A., Nielsen, S.G. (2013) Nuclear field shift in natural environments. Comptes Rendus Geoscience 345, 150–159. https://doi.org/10.1016/j.crte.2013.01.004
 Show in context
Show in context These isotope exchange reactions have been assumed to be equilibrium processes (Fujii et al., 2009), and the nuclear field shift effect (NFSE) itself has thus far been calculated only for equilibrium exchange reactions (Bigeleisen, 1996; Moynier et al., 2013).
View in article
These anomalous fractionations are consistent with those observed previously for U isotopes in chemical exchange reactions, in which fractionation factors for each isotope scale better with the mean square nuclear charge radii rather than the isotope mass (Fig. S-4), indicating that the nuclear volume dominates the fractionation (Fujii et al., 2009; Moynier et al., 2013).
View in article
On the other hand, the NFSE may be exclusively an equilibrium fractionation between the instantaneous products and transition state(s), and the transition state(s) and the reactants, and as such, its expression during kinetic fractionation within the reduction reaction may be dependent on reaction reversibility (Fujii et al., 2009; Moynier et al., 2013; Yang and Liu, 2016; Sato et al., 2021).
View in article
Nomura, M., Higuchi, N., Fujii, Y. (1996) Mass Dependence of Uranium Isotope Effects in the U(IV)−U(VI) Exchange Reaction. Journal of the American Chemical Society 118, 9127–9130. https://doi.org/10.1021/ja954075s
 Show in context
Show in context Further, isotope exchange reactions have revealed anomalous fractionations of the odd-mass isotopes, i.e. 233U and 235U, which deviate from the linear relationship between mass and fractionation magnitude observed for the even-mass isotopes (Fujii et al., 1989a, 1989b; Nomura et al., 1996).
View in article
Sato, A., Bernier-Latmani, R., Hada, M., Abe, M. (2021) Ab initio and steady-state models for uranium isotope fractionation in multi-step biotic and abiotic reduction. Geochimica et Cosmochimica Acta 307, 212–227. https://doi.org/10.1016/j.gca.2021.05.044
 Show in context
Show in context Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
However, previous calculations using the HF method showed better agreement with the experimental ɛeq for the UVI/UIV-chloride isotope exchange reaction compared with DFT calculations, suggesting that the results of the HF method may be more accurate (Wang et al., 2015; Sato et al., 2021).
View in article
The mathematical basis for the inclusion of NFSE in kinetic fractionation has been derived by Sato et al. (2021).
View in article
On the other hand, the NFSE may be exclusively an equilibrium fractionation between the instantaneous products and transition state(s), and the transition state(s) and the reactants, and as such, its expression during kinetic fractionation within the reduction reaction may be dependent on reaction reversibility (Fujii et al., 2009; Moynier et al., 2013; Yang and Liu, 2016; Sato et al., 2021).
View in article
Schauble, E.A. (2007) Role of nuclear volume in driving equilibrium stable isotope fractionation of mercury, thallium, and other very heavy elements. Geochimica et Cosmochimica Acta 71, 2170–2189. https://doi.org/10.1016/j.gca.2007.02.004
 Show in context
Show in context Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996; Schauble, 2007; Stirling et al., 2015), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010; Basu et al., 2014, 2020; Stirling et al., 2015).
View in article
Stirling, C.H., Andersen, M.B., Warthmann, R., Halliday, A.N. (2015) Isotope fractionation of 238U and 235U during biologically-mediated uranium reduction. Geochimica et Cosmochimica Acta 163, 200–218. https://doi.org/10.1016/j.gca.2015.03.017
 Show in context
Show in context Furthermore, given that hexavalent U (UVI) reduction in the laboratory and nature display the same direction of fractionation as predicted for equilibrium (Bigeleisen, 1996; Schauble, 2007; Stirling et al., 2015), the nuclear field shift was also implicated for kinetically controlled reactions (Bopp et al., 2010; Basu et al., 2014, 2020; Stirling et al., 2015).
View in article
These values are very typical for these biologically mediated reactions and demonstrate the sequestration of the isotopically heavy UIV product from the reactants, as shown previously for U isotope fractionation (Basu et al., 2014; Stirling et al., 2015; Stylo et al., 2015).
View in article
Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Stylo, M., Neubert, N., Wang, Y., Monga, N., Romaniello, S.J., Weyer, S., Bernier-Latmani, R. (2015) Uranium isotopes fingerprint biotic reduction. Proceedings of the National Academy of Sciences 112, 5619–5624. https://doi.org/10.1073/pnas.1421841112
 Show in context
Show in context These values are very typical for these biologically mediated reactions and demonstrate the sequestration of the isotopically heavy UIV product from the reactants, as shown previously for U isotope fractionation (Basu et al., 2014; Stirling et al., 2015; Stylo et al., 2015).
View in article
Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
Wall, J.D., Krumholz, L.R. (2006) Uranium Reduction. Annual Review of Microbiology 60, 149–166. https://doi.org/10.1146/annurev.micro.59.030804.121357
 Show in context
Show in context This well documented reaction leads to the reductive precipitation of solid phase UIV through the extracellular transfer of electrons via enzymes on the bacterial surface (Wall and Krumholz, 2006).
View in article
Wang, X., Johnson, T.M., Lundstrom, C.C. (2015) Low temperature equilibrium isotope fractionation and isotope exchange kinetics between U(IV) and U(VI). Geochimica et Cosmochimica Acta 158, 262–275. https://doi.org/10.1016/j.gca.2015.03.006
 Show in context
Show in context These observations suggest that, whilst ongoing equilibrium isotope exchange may make a minor contribution to the observed direction of the fractionation (enrichment of the heavy isotope in the UIV product, as demonstrated by Wang et al., 2015), it does not account for the magnitude of isotope fractionation during the kinetic reaction of biological reduction.
View in article
Kinetic fractionations of U isotopes in the laboratory and nature consistently show lower fractionation than that predicted or measured at equilibrium (Fujii et al., 2006; Abe et al., 2008, 2010; Basu et al., 2014; Wang et al., 2015; Stirling et al., 2015; Stylo et al., 2015; Andersen et al., 2017; Brown et al., 2018; Sato et al., 2021; Li and Tissot, 2023).
View in article
However, previous calculations using the HF method showed better agreement with the experimental ɛeq for the UVI/UIV-chloride isotope exchange reaction compared with DFT calculations, suggesting that the results of the HF method may be more accurate (Wang et al., 2015; Sato et al., 2021).
View in article
Yang, S., Liu, Y. (2016) Nuclear field shift effects on stable isotope fractionation: a review. Acta Geochimica 35, 227–239. https://doi.org/10.1007/s11631-016-0109-3
 Show in context
Show in context On the other hand, the NFSE may be exclusively an equilibrium fractionation between the instantaneous products and transition state(s), and the transition state(s) and the reactants, and as such, its expression during kinetic fractionation within the reduction reaction may be dependent on reaction reversibility (Fujii et al., 2009; Moynier et al., 2013; Yang and Liu, 2016; Sato et al., 2021).
View in article
Zheng, W., Hintelmann, H. (2010) Nuclear Field Shift Effect in Isotope Fractionation of Mercury during Abiotic Reduction in the Absence of Light. The Journal of Physical Chemistry A 114, 4238–4245. https://doi.org/10.1021/jp910353y
 Show in context
Show in context Whilst the NFSE has been observed during abiotic and kinetic fractionations of Hg isotopes (Zheng and Hintelmann, 2010), to our knowledge, there is no evidence of the NFSE during the biotic fractionation of any element.
View in article
Further work is required to explore the factors that control the relative contributions of the two effects during kinetic isotope fractionations and rule out the contribution of other isotope effects, e.g., a nuclear spin effect or magnetic isotope effect (Epov et al., 2011). Indeed, different reaction mechanisms of Hg reduction, e.g., photoreduction versus reduction by dissolved organic matter or SnCl2, resulted in different relative contributions of mass-dependent and mass-independent fractionation (Bergquist and Blum, 2007; Zheng and Hintelmann, 2010).
View in article
top
Supplementary Information
The Supplementary Information includes:
- Experimental Section
- Table S-1
- Figures S-1 to S-6
- Supplementary Information References
Download the Supplementary Information (PDF)
Figures
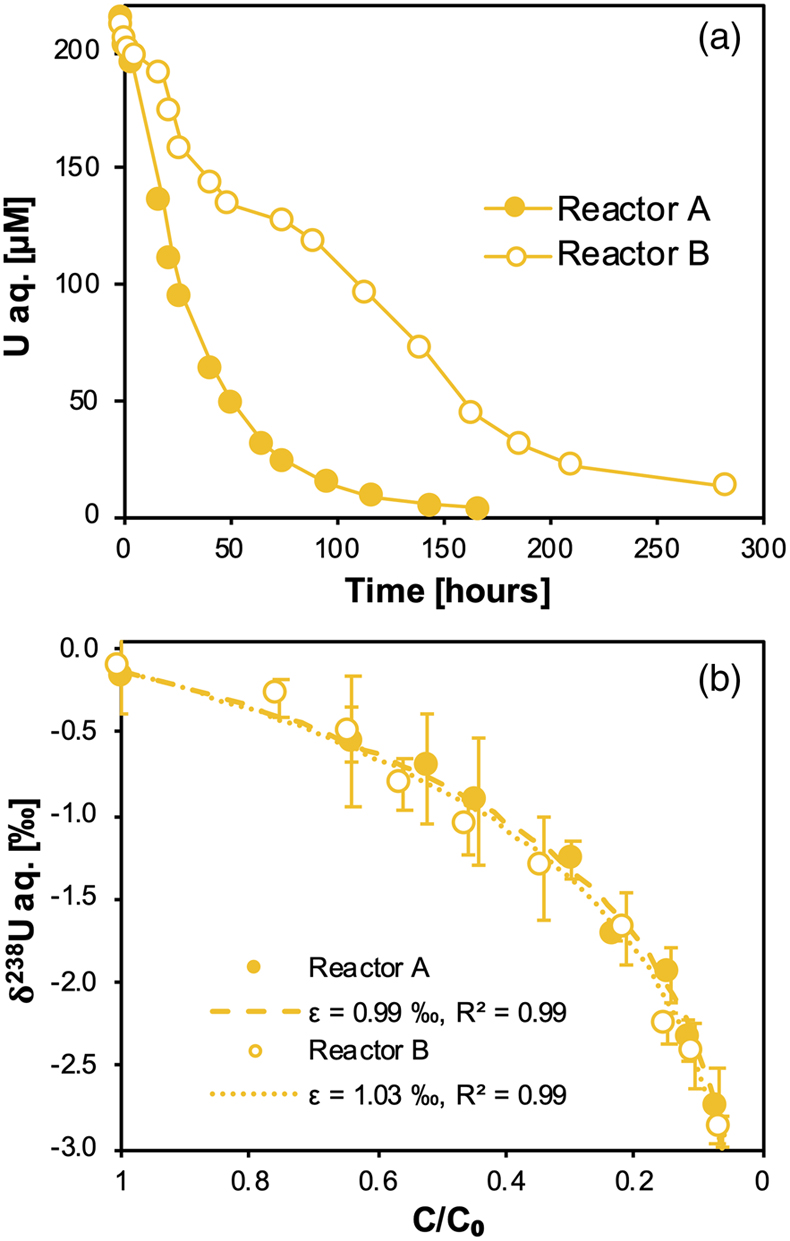
Figure 1 (a) Concentration of aqueous U (representing UVI), as a function of time, in reactors containing 200 μM UVI and 30 mM sodium bicarbonate incubated with S. oneidensis. Filled and open symbols depict duplicate reactors. (b) δ238U values for aqueous U reported as a function of the remaining aqueous U fraction. Filled and open symbols depict duplicate reactors and error bars show 2 standard deviations of the mean of triplicate measurements. Rayleigh model curves for each duplicate reactor are shown in dashed lines, along with their corresponding isotope enrichment factors (ɛ). See Supplementary Information for definition of δ238U.
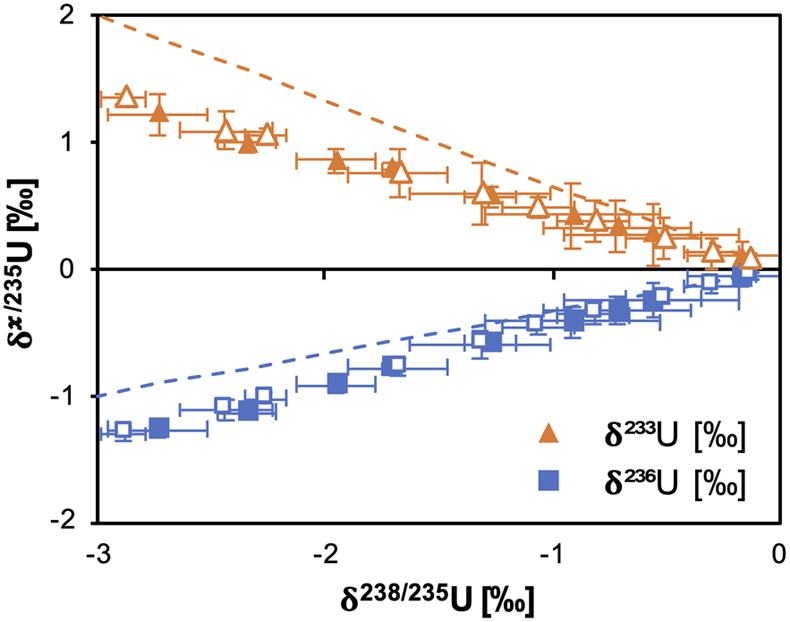
Figure 2 Three-isotope plots for delta values of all samples. Filled and open symbols depict duplicate reactors and error bars show two standard deviations of the mean of triplicate measurements. Dashed lines represent theoretical relationships for mass-dependent fractionation.
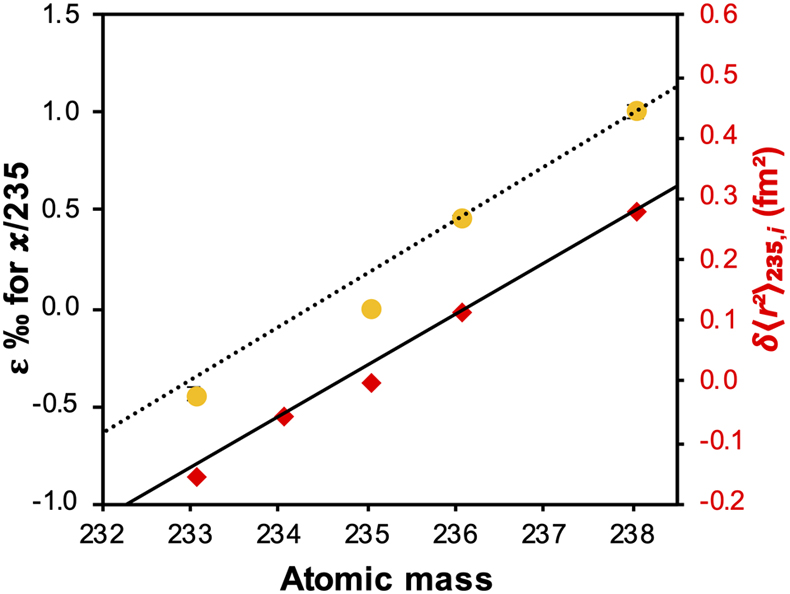
Figure 3 Fractionation factors (ɛ) for each atomic mass. Symbols and error bars depict the mean and standard deviation of duplicate reactors. Where not visible, the error is within the size of the symbol. Mean square nuclear charge radii (δ〈r2〉235,i =δ〈r2〉i − δ〈r2〉235) for each atomic mass were taken from Angeli and Marinova (2013)
Angeli, I., Marinova, K.P. (2013) Table of experimental nuclear ground state charge radii: An update. Atomic Data and Nuclear Data Tables 99, 69–95. https://doi.org/10.1016/j.adt.2011.12.006
. The lines represent linear regressions of ɛ and δ〈r2〉235,i for even-mass numbers only.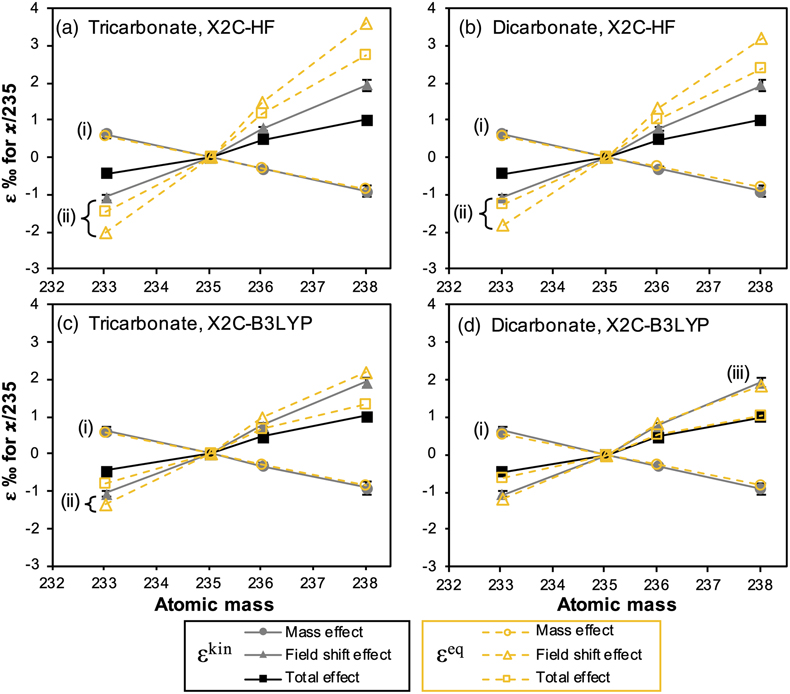
Figure 4 Isotope enrichment factors from the bacterial reduction experiment (ɛkin) and ab initio calculated equilibrium isotope enrichment factors (ɛeq) for the mass effect, the nuclear field shift effect and their sum (total effect) for each atomic mass. Equilibrium calculations were performed for either (a, c) tricarbonate, UO2(CO3)34−, or (b, d) dicarbonate, UO2(CO3)22−, as the UVI species. Calculations of ln Knv for ɛeq were performed using either (a, b) the Hartree-Fock method (X2C-HF) or (c, d) density functional theory (DFT) with the B3LYP functional (X2C-B3LYP). Symbols and error bars depict the mean and standard deviation of values derived from analysis of the data from duplicate reactors. A comparison of experimentally measured ɛ and recalculated total ɛ (after decomposition of the experimental data into the field shift and mass effect terms) is presented in Figure S-6. Trend (i) points to the consistent values obtained for MDF from theory and experiment, (ii) points to the discrepancy between theory and experiment for the NFSE contribution in three of the four cases, and (iii) points to the agreement between NFSE theory and experiment in the case of dicarbonate speciation and DFT calculations.