Temporal variation in relative zircon abundance throughout Earth history
Affiliations | Corresponding Author | Cite as | Funding informationKeywords: geochronology, crustal evolution, zircon, hadean
- Share this article
Article views:9,638Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
Abstract
Figures and Tables
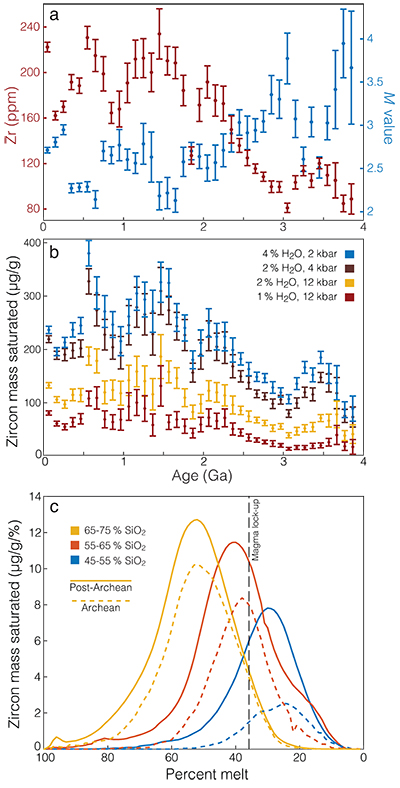 Figure 1 (a) Average zirconium and M value throughout the preserved rock record for continental igneous rocks with 40–80 % SiO2. (b) Calculated average zircon concentration (micrograms of zircon per gram of whole rock) as a function of time, under a range of possible crystallisation conditions. (c) Zircon saturation distributions during magma crystallisation as a function of percent melt for varying silica ranges, calculated at 6 kilobar and 3 wt. % H2O. Relative zircon abundance is reported as micrograms of zircon saturated per gram of magma per percentage-point decrease in residual melt fraction. All uncertainties are two standard error of the mean. | 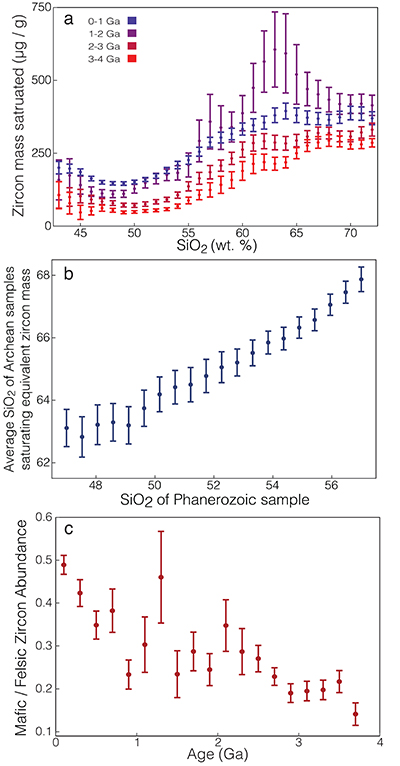 Figure 2 Temporal variability in the distribution of zircon between igneous rocks of different silica contents, calculated at 6 kilobar and 3 wt. % H2O. (a) Temporal variation in relative zircon abundance as a function of silica. (b) Line of silica equivalence between Archean and Phanerozoic samples (the silica contents required to saturate the same mass of zircon in Archean and Phanerozoic magmas). (c) The mass of zircon saturated per mass of mafic magma (43–53 % SiO2) relative to that saturated in an equivalent mass of coeval felsic magma (63–73 % SiO2). The likelihood of saturating zircon in mafic lithologies was dramatically lower (by a factor of nearly 5) in the earliest Archean than it is today. All uncertainties are two standard error of the mean. | 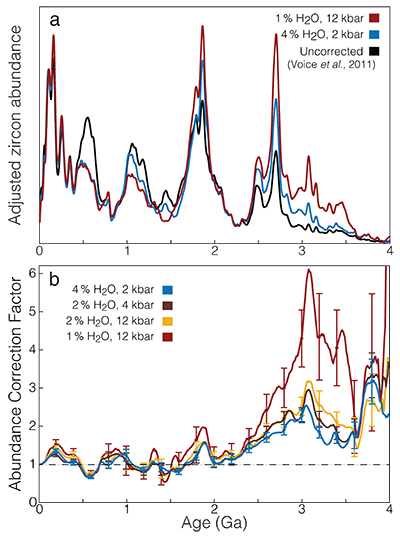 Figure 3 (a) The effect of applying a relative zircon abundance correction (normalising to constant magma zircon productivity) to the detrital zircon age spectrum of Voice et al. (2011) for varying crystallisation conditions. (b) The average mass of magma throughout Earth history required to produce the same mass of zircon as a unit mass of average present-day magma. |
| Figure 1 | Figure 2 | Figure 3 |
Supplementary Figures and Tables
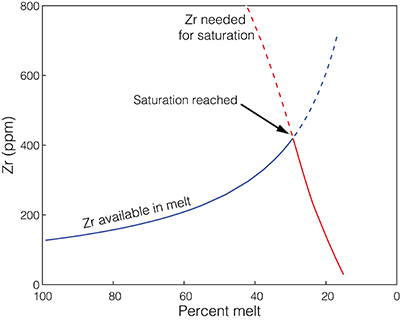 Figure S-1 Zirconium evolution and the point of zircon saturation during a crystallisation simulation for a single whole rock composition, in this case a basaltic andesite composition. Zirconium concentration in the melt increases during differentiation as a generally incompatible element, while both temperature and M-value decrease with increasing crystallinity, decreasing the zirconium concentration required to saturate zircon. | 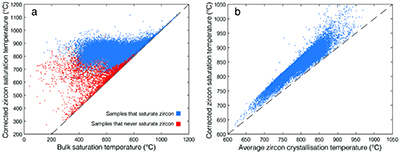 Figure S-2 The relationship between bulk zircon saturation temperatures, corrected zircon saturation temperatures, and average zircon crystallisation temperatures during closed system equilibrium crystallisation for 52,300 whole rock compositions. Bulk saturation temperature is the result of applying the equation of Boehnke et al. (2013) directly to each whole rock composition. (a) Corrected zircon saturation temperature adjusts for differentiation during in situ crystallisation, resulting in consistently higher saturation temperatures relative to bulk saturation temperature, as observed in panel. For samples that do not ever saturate zircon, the highest saturation temperature of any differentiated melt is reported. (b) For samples which do saturate zircon, average zircon crystallisation temperature is the weighted average of the zircon crystallisation temperature distribution, resulting in temperatures closely correlated with, but necessarily colder than, the adjusted zircon saturation temperature. While not highly sensitive to pressure or water content, the values shown here are calculated for shallow, water saturated conditions (2 kbar and 4 wt. % H2O). | 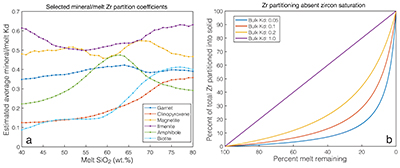 Figure S-3 Zirconium partitioning. (a) Zirconium mineral/melt partition coefficients for several minerals with non-negligible zirconium compatibility. Partition coefficients shown are averages of GERM partition coefficient data fit as a function of melt SiO2. Uncertainties are omitted for visibility. (b) The proportion of the total zirconium budget partitioned into the solid at equilibrium as a function of remaining melt percent and mineral/melt partition coefficient. | 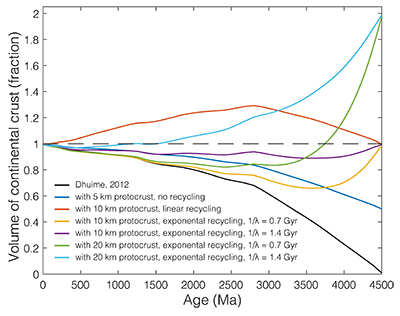 Figure S-4 A selection of possible crustal growth curves with varying initial boundary conditions (no crust, 5, 10, and 20 km thick primordial anorthosite floatation crust) and functional form of the recycling term (none, linear, and exponential with 0.7 or 1.4 Gyr e-folding time 1/λ). Exponential recycling rates are considered based on the possibility that crustal recycling rate may have been faster in the past as a direct and indirect result of higher mantle potential temperature. |
| Figure S-1 | Figure S-2 | Figure S-3 | Figure S-4 |
top
Letter
The accessory mineral zircon is ubiquitous, refractory, and readily radiometrically dated to high precision and accuracy through the U and Th decay systems. This trinity of properties has made zircon into a standard mineral tracer of geologic time, resolving timescales from Gyr to kyr through the related U-Th/Pb and U-series geochronometers (e.g., Schmitt, 2011
Schmitt, A.K. (2011) Uranium Series Accessory Crystal Dating of Magmatic Processes. Annual Review of Earth and Planetary Sciences 39, 321–349.
; Schoene, 2014Schoene, B. (2014) 4.10 U–Th–Pb Geochronology. In: Rudnick, R.L. (Ed.) Treatise on Geochemistry Volume 4: The Crust. Second edition. Elsevier, Amsterdam, 341–378.
). Zircons constitute the oldest known terrestrial material, providing a glimpse of Earth in the Hadean Eon which has been argued to reveal a remarkably modern environment, complete with liquid water (Mojzsis et al., 2001Mojzsis, S.J., Harrison, T.M., Pidgeon, R.T. (2001) Oxygen-isotope evidence from ancient zircons for liquid water at the Earth’s surface 4,300 Myr ago. Nature 409, 178–181.
; Wilde et al., 2001Wilde, S.A., Valley, J.W., Peck, W.H., Graham, C.M. (2001) Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago. Nature 409, 175–178.
) and felsic crust (Harrison, 2009Harrison, T.M. (2009) The Hadean Crust: Evidence from ¿4 Ga Zircons. Annual Review of Earth and Planetary Sciences 37, 479–505.
). Given its ubiquity in igneous rocks, zircon has been used as a proxy for magma crystallisation, crust production, and even crustal composition (Condie et al., 2009Condie, K.C., Belousova, E., Griffin, W.L., Sircombe, K.N. (2009) Granitoid events in space and time: Constraints from igneous and detrital zircon age spectra. Gondwana Research 15, 228–242.
; Cawood et al., 2013Cawood, P.A., Hawkesworth, C.J., Dhuime, B. (2013) The continental record and the generation of continental crust. Geological Society of America Bulletin 125, 14–32.
; Parman, 2015Parman, S.W. (2015) Time-lapse zirconography: Imaging punctuated continental evolution. Geochemical Perspectives Letters 1, 43–52.
; Lee et al., 2016Lee, C.-T.A., Yeung, L.Y., McKenzie, N.R., Yokoyama, Y., Ozaki, K., Lenardic, A. (2016) Two-step rise of atmospheric oxygen linked to the growth of continents. Nature Geoscience 9, 417–424.
). However, quantity of zircon is not a direct substitute for quantity of magma or crust. Instead, zircon abundance in the igneous record is a function of magma composition, which is both spatially and temporally heterogeneous. Moreover, due to the high closure temperatures of the U-Th/Pb and U-series systems, ages from these geochronometers exclusively date zircon crystallisation (Schoene, 2014Schoene, B. (2014) 4.10 U–Th–Pb Geochronology. In: Rudnick, R.L. (Ed.) Treatise on Geochemistry Volume 4: The Crust. Second edition. Elsevier, Amsterdam, 341–378.
), which need not coincide with the crystallisation of other silicate minerals.The temperature Tsat at which zircon saturates in an igneous magma can be accurately predicted by an empirical equation of the form
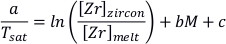
where a, b, and c are constants, [Zr] is zirconium concentration, and M is a compositional measure of magma polymerisation defined on a molar basis as
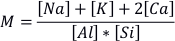
(Watson and Harrison, 1983
Watson, E.B., Harrison, T.M. (1983) Zircon saturation revisited: temperature and composition effects in a variety of crustal magma types. Earth and Planetary Science Letters 64, 295–304.
; Boehnke et al., 2013Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
). Purely stochastic heterogeneity in magma composition would produce no meaningful temporal variation in zircon saturation behaviour. However, on sufficiently long geologic timescales, decreasing mantle potential temperature from the early Earth to the present is reflected in systematic variations in average magma composition, including increasing abundance of incompatible elements such as Zr (Keller and Schoene, 2012Keller, C.B., Schoene, B. (2012) Statistical geochemistry reveals disruption in secular lithospheric evolution about 2.5Gyr ago. Nature 485, 490– 493.
).Even within a closed system, magma composition (including M and [Zr]melt) varies systematically throughout crystallisation as a function of pressure, temperature, and melt fraction, such that a single bulk zircon saturation temperature is insufficient to characterise the zircon saturation behaviour of simple igneous systems (e.g., Harrison et al., 2007
Harrison, T.M., Watson, E.B., Aikman, A.B. (2007) Temperature spectra of zircon crystallization in plutonic rocks. Geology 35, 635.
). Accordingly, in order to examine the effects of temporal variations in magma composition throughout Earth history on zircon saturation behaviour, we combine zircon saturation calculations with alphaMELTS (Ghiorso et al., 2002Ghiorso, M.S., Hirschmann, M.M., Reiners, P.W., Kress, V.C.III (2002) The pMELTS: A revision of MELTS for improved calculation of phase relations and major element partitioning related to partial melting of the mantle to 3 GPa. Geochemistry Geophysics Geosystems 3, 1–36.
; Smith and Asimow, 2005Smith, P.M., Asimow, P.D. (2005) Adiabat 1ph: A new public front-end to the MELTS, pMELTS, and pHMELTS models. Geochemistry Geophysics Geosystems 6, 1–8.
) major element simulations on 52,300 whole rock compositions spanning the preserved rock record from modern to Archean. While generally incompatible in silicate minerals, zirconium mineral/melt partition coefficients vary widely between common silicate minerals and may be as high as 0.3–0.5 for clinopyroxene, amphibole, and garnet. Consequently, to ensure accurate zircon saturation calculations, mineral-specific partition coefficients from the Geochemical Earth Reference Model database (GERM, 2013GERM (2013) Geochemical Earth Reference Model Partition Coefficient Database. http://www.earthref.org/KDD/
) were used when calculating melt Zr concentrations at each temperature step of each alphaMELTS simulation. Finally, to obtain temporal trends, the results of zircon saturation simulations were subjected to weighted bootstrap re-sampling following the approach of Keller and Schoene (2012)Keller, C.B., Schoene, B. (2012) Statistical geochemistry reveals disruption in secular lithospheric evolution about 2.5Gyr ago. Nature 485, 490– 493.
, to calculate accurate estimates of the mean and standard error of the mean for each independent variable of interest.The primary forcings on zircon abundance over Gyr timescales are illustrated in Figure 1a as averages for igneous whole rock samples preserved in the present-day continental crust. Over the past 4 Gyr, average igneous zirconium content has increased, while average M-value has decreased. These changes are a consequence of secular mantle cooling, where lower average mantle melting extent has led to increased average concentrations of incompatible elements such as Zr (Keller and Schoene, 2012
Keller, C.B., Schoene, B. (2012) Statistical geochemistry reveals disruption in secular lithospheric evolution about 2.5Gyr ago. Nature 485, 490– 493.
), and generally lower M values due to lower Ca and higher Al abundance. Combined, these forcings should result in substantially increased zircon concentration in the igneous record (mass of zircon crystallised per mass of magma) since the early Archean.Figure 1 (a) Average zirconium and M value throughout the preserved rock record for continental igneous rocks with 40–80 % SiO2. (b) Calculated average zircon concentration (micrograms of zircon per gram of whole rock) as a function of time, under a range of possible crystallisation conditions. (c) Zircon saturation distributions during magma crystallisation as a function of percent melt for varying silica ranges, calculated at 6 kilobar and 3 wt. % H2O. Relative zircon abundance is reported as micrograms of zircon saturated per gram of magma per percentage-point decrease in residual melt fraction. All uncertainties are two standard error of the mean.
While zircon saturation is largely independent of magma pressure and water content (Boehnke et al., 2013
Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
), the crystallisation of other silicate minerals is not, with higher pressure and lower water content generally increasing crystallisation temperatures. Consequently, in drier or deeper magmas, most silicate minerals will crystallise early relative to zircon (Keller et al., 2015Keller, C.B., Schoene, B., Barboni, M., Samperton, K.M., Husson, J.M. (2015) Volcanic–plutonic parity and the differentiation of the continental crust. Nature 523, 301–307.
); such magmas will be more likely to crystallise fully to the solidus without ever reaching zircon saturation. Correspondingly, saturation simulations run at higher pressures or lower magma water contents display lower total zircon abundance at any given time, as shown in Figure 1b. Nonetheless, common temporal trends are revealed across a wide range of P and H2O values, with the mass of zircon saturated per mass of magma increasing substantially since the early Archean (Fig. 1b). The influence of crystallisation pressure and magma water content on final whole rock zircon limits our ability to reconstruct unambiguously past magma volumes from the zircon record. However, proposed scenarios of constant or decreasing crustal thickness (e.g., Keller and Schoene, 2012Keller, C.B., Schoene, B. (2012) Statistical geochemistry reveals disruption in secular lithospheric evolution about 2.5Gyr ago. Nature 485, 490– 493.
) and constant or increasing magma water content from the Archean to the present would, if anything, accentuate the trends observed in Figure 1.Changing average zirconium concentration and M value over the past ∼4 Gyr have additional consequences for the position of zircon in the magma crystallisation sequence. In general, mafic magmas require greater extents of in situ differentiation to reach zircon saturation, and thus crystallise zircon at lower residual melt fractions (Fig. 1c). As observed in Figure 1c, zircon saturation in Archean magmas of any given silica range is further delayed and diminished due to lower average [Zr] and higher M-values. Unsurprisingly, delayed zircon saturation is directly correlated with lower total zircon mass saturated (Fig. 1c), an effect that is accentuated if a magma is not allowed to cool fully to its solidus, either due to eruptive quenching or residual melt extraction.
Due to non-Newtonian magma rheology, magmas containing less than ∼37 % melt are disproportionately unlikely to erupt (Caricchi et al., 2007
Caricchi, L., Burlini, L., Ulmer, P., Gerya, T. (2007) Non-Newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics. Earth and Planetary Science Letters 264, 402–419.
); common volcanic rocks are typically well above this threshold. As residual melt is largely quenched to an amorphous glass upon eruption, any mineral phases crystallising below the eruptive melt fraction will be absent from the volcanic record. Given that basalts display the greatest delay in zircon saturation and are substantially over-represented in the volcanic record (Keller et al., 2015Keller, C.B., Schoene, B., Barboni, M., Samperton, K.M., Husson, J.M. (2015) Volcanic–plutonic parity and the differentiation of the continental crust. Nature 523, 301–307.
), the effect of eruptive quenching on zircon saturation will be most noticeable in the mafic record. Phanerozoic basalts typically erupt with fewer than 30 % phenocrysts by volume (e.g., Bryan, 1983Bryan, W.B. (1983) Systematics of modal phenocryst assemblages in submarine basalts: Petrologic implications. Contributions to Mineralogy and Petrology 83, 62–74.
), and at the time of eruption contain little or no zircon, as expected from Figure 1c. Delayed zircon saturation in Archean lithologies should result in an even more pronounced dearth of zircons in the Archean volcanic record for magmas of any given silica content consistent with the observations in Eoarchean volcaniclastic metasediments, e.g., Kamber et al. (2005)Kamber, B.S., Whitehouse, M., Bolhar, R., Moorbath, S. (2005) Volcanic resurfacing and the early terrestrial crust: Zircon U–Pb and REE constraints from the Isua Greenstone Belt, southern West Greenland. Earth and Planetary Science Letters 240, 276–290.
.As shown in Figure 2a, Archean mafic magmas saturated on average very little zircon per mass of whole rock both relative to either Archean felsic rocks or post-Archean mafic rocks when crystallised to their solidus at a given set of P, H2O conditions. This dramatic deficit is equivalent to a difference of more than 10 wt. % silica in whole rock composition, such that for example, an Archean granodiorite with 65 wt. % SiO2 saturates only as much zircon as a Phanerozoic basalt with 53 wt. % SiO2 (Fig. 2b).
Moreover, while felsic magmas in Figure 2a consistently saturate more zircon on average than their mafic counterparts at all times in Earth history, this relative imbalance was stronger in the Archean. Figure 2c illustrates the calculated average mass of zircon saturated during complete crystallisation of a given mass of mafic magma (43–53 % SiO2) relative to that saturated in an equal mass of coeval felsic magma (63–73 % SiO2). As observed in Figure 2c, the discrepancy between mafic and felsic zircon abundance is roughly three times greater in the Archean, with Archean mafic magmas crystallising on average little more than a tenth of the zircon mass saturated by an equal mass of coeval felsic magma when both are fully crystallised. This inequality between Archean mafic and felsic zircon abundance is exacerbated when considering magmas that do not fully crystallise, due to the greatly delayed zircon saturation of Archean mafic magmas (Fig. 1c) – an effect that would be further compounded by the apparent prevalence of volcanic lithologies in the Archean mafic record (e.g., de Wit and Ashwal, 1997
de Wit, M.J., Ashwal, L.D. (1997) Greenstone belts. Oxford University Press, Oxford.
).Figure 2 Temporal variability in the distribution of zircon between igneous rocks of different silica contents, calculated at 6 kilobar and 3 wt. % H2O. (a) Temporal variation in relative zircon abundance as a function of silica. (b) Line of silica equivalence between Archean and Phanerozoic samples (the silica contents required to saturate the same mass of zircon in Archean and Phanerozoic magmas). (c) The mass of zircon saturated per mass of mafic magma (43–53 % SiO2) relative to that saturated in an equivalent mass of coeval felsic magma (63–73 % SiO2). The likelihood of saturating zircon in mafic lithologies was dramatically lower (by a factor of nearly 5) in the earliest Archean than it is today. All uncertainties are two standard error of the mean.
If not accounted for, systematic temporal variations in relative zircon abundance would lead to substantial underestimation of the amount of crust required to produce Earth’s early zircon record. The impact of this trend on preserved zircon age spectra is shown in Figure 3a, which illustrates how the zircon age spectrum of Voice et al. (2011)
Voice, P.J., Kowalewski, M., Eriksson, K.A. (2011) Quantifying the Timing and Rate of Crustal Evolution: Global Compilation of Radiometrically Dated Detrital Zircon Grains. The Journal of Geology 119, 109–126.
would differ if magmas throughout Earth history had crystallised zircon at present-day rates, for a range of assumed model conditions. For magmas crystallising at a given set of P, H2O conditions, this result is equivalent to the true magma age spectrum required to produce the observed detrital zircon age spectrum in the absence of preservation bias – with true average crystallisation conditions likely intermediate between the shallow/wet and deep/dry endmembers shown in Figure 3a. As peaks in global zircon age spectra are often interpreted as times of increased global magmatic activity, correlated with the plate tectonic Wilson cycle (e.g., Condie and Aster, 2010Condie, K.C., Aster, R.C. (2010) Episodic zircon age spectra of orogenic granitoids: The supercontinent connection and continental growth. Precambrian Research 180, 227–236.
), the corrected age spectrum may imply a more steady-state supercontinent cycle with similar maxima in magmatic activity to ∼3 Ga, or (depending on the strength of preservation bias) even before.Figure 3 (a) The effect of applying a relative zircon abundance correction (normalising to constant magma zircon productivity) to the detrital zircon age spectrum of Voice et al. (2011)
Voice, P.J., Kowalewski, M., Eriksson, K.A. (2011) Quantifying the Timing and Rate of Crustal Evolution: Global Compilation of Radiometrically Dated Detrital Zircon Grains. The Journal of Geology 119, 109–126.
for varying crystallisation conditions. (b) The average mass of magma throughout Earth history required to produce the same mass of zircon as a unit mass of average present-day magma.The zircon abundance correction increases the magmatic significance of the Archean and Proterozoic zircon record, and appears to improve the correspondence in magnitude between temporally correlated zircon abundance maxima and mantle depletion events (e.g., Pearson et al., 2007
Pearson, D.G., Parman, S.W., Nowell, G.M. (2007) A link between large mantle melting events and continent growth seen in osmium isotopes. Nature 449, 202–205.
). Considering present-day zircon productivity levels, three to five times more Archean magma was required to produce a given amount of zircon (Fig. 3b); such corrections should be applied to models relying on zircon abundance as a proxy for crust or magma extent.If Hadean mantle potential temperatures were equal to or greater than those of the early Archean, we might infer that zircon saturation was inhibited in Hadean mafic magmas by a factor equal to or greater than that of the early Archean. This would decrease the likelihood that any given Hadean zircon originated from a mafic lithology by more than a factor of three relative to an equivalent model where systematic temporal trends in whole rock geochemistry are neglected.
While the above considerations are applicable in principle to zircon-based crustal growth models such as those of Belousova et al. (2010)
Belousova, E., Kostitsyn, Y., Griffin, W.L., Begg, G.C., O’Reilly, S.Y., Pearson, N.J. (2010) The growth of the continental crust: Constraints from zircon Hf-isotope data. LITHOS 119, 457–466.
or Dhuime et al. (2012)Dhuime, B., Hawkesworth, C.J., Cawood, P.A., Storey, C.D. (2012) A Change in the Geodynamics of Continental Growth 3 Billion Years Ago. Science 335, 1334–1336.
, a simple correction factor as in Figure 3b alone is likely insufficient. Firstly, applying the models of Figure 3 to a crustal growth curve assumes closed system crystallisation at crustal scale. While this may seem a minor assumption, it does not necessarily hold in the early Hadean: a terrestrial flotation cumulate, for instance, would systematically exclude dense zircon. Consistent with this expectation, lunar anorthosites contain only 0.1–0.5 ppm zirconium (e.g., several hundred times lower than an average Archean basalt), offset by zirconium enrichments up to 2000 ppm in complementary KREEP basalts (Ehmann et al., 1979Ehmann, W.D., Chyi, L.L., Garg, A.N., Ali, M.Z. (1979) The distribution of zirconium and hafnium in terrestrial rocks, meteorites and the moon. Physics and Chemistry of the Earth 11, 247–259.
). Such extreme zirconium deficiency in Lunar anorthosites indicates that the most likely candidate lithology for primordial terrestrial crust is effectively invisible to zircon-based crustal growth models. Secondly, the insensitivity of zircon saturation to water content along with Zr immobility in aqueous fluids implies that most subducted zircon will not return to the crust in new arc magmas—a corollary to the well-known arc signature of high field-strength element depletion. Consequently, while zircon-based crustal growth models account for crustal magmatic reworking, crustal destruction by sediment subduction and subduction-erosion will be largely undetectable in the zircon record. Together, these specific issues arising from the crystallisation and stability of zircon suggest that both initial crustal volume and subsequent net growth or destruction rate are poorly bounded and subject to assumptions (e.g., Fig. S-4).Together, our results emphasise the significance of the extant zircon record of early Earth history, given the difficulty of saturating zircon under early Earth conditions due to lower average magma zirconium content and lower silicate magma polymerisation state. Under such conditions, zircon saturation is delayed and diminished, especially in mafic lithologies. Consequently, more crust is required to explain preserved zircon age spectra, and a potentially significant volume of felsic crust is favoured as the likely source of preserved Hadean zircons.
top
Acknowledgements
C.B.K. was supported in part by the Department of Energy Computational Science Graduate Fellowship Program of the Office of Science and National Nuclear Security Administration in the Department of Energy under contract DE-FG02-97ER25308. Computational resources were provided by the Princeton Institute for Computational Science and Engineering.
Editor: Graham Pearson
top
Author Contributions
C.B.K. conducted the calculations and prepared the manuscript. All authors contributed to the design of the study and the interpretation of the results.
top
Data Availability
All data and source code used in this study is freely available at https://github.com/brenhinkeller/meltstzirc.
top
References
Belousova, E., Kostitsyn, Y., Griffin, W.L., Begg, G.C., O’Reilly, S.Y., Pearson, N.J. (2010) The growth of the continental crust: Constraints from zircon Hf-isotope data. LITHOS 119, 457–466.
Show in context While the above considerations are applicable in principle to zircon-based crustal growth models such as those of Belousova et al. (2010) or Dhuime et al. (2012), a simple correction factor as in Figure 3b alone is likely insufficient.
View in article
Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
Show in contextThe temperature Tsat at which zircon saturates in an igneous magma can be accurately predicted by an empirical equation of the form 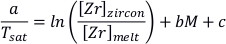where a, b, and c are constants, [Zr] is zirconium concentration, and M is a compositional measure of magma polymerisation defined on a molar basis as 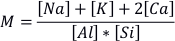(Watson and Harrison, 1983; Boehnke et al., 2013).
View in article
While zircon saturation is largely independent of magma pressure and water content (Boehnke et al., 2013), the crystallisation of other silicate minerals is not, with higher pressure and lower water content generally increasing crystallisation temperatures.
View in article
Bryan, W.B. (1983) Systematics of modal phenocryst assemblages in submarine basalts: Petrologic implications. Contributions to Mineralogy and Petrology 83, 62–74.
Show in context Phanerozoic basalts typically erupt with fewer than 30 % phenocrysts by volume (e.g., Bryan, 1983), and at the time of eruption contain little or no zircon, as expected from Figure 1c.
View in article
Caricchi, L., Burlini, L., Ulmer, P., Gerya, T. (2007) Non-Newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics. Earth and Planetary Science Letters 264, 402–419.
Show in context Due to non-Newtonian magma rheology, magmas containing less than ∼37 % melt are disproportionately unlikely to erupt (Caricchi et al., 2007); common volcanic rocks are typically well above this threshold.
View in article
Cawood, P.A., Hawkesworth, C.J., Dhuime, B. (2013) The continental record and the generation of continental crust. Geological Society of America Bulletin 125, 14–32.
Show in context Given its ubiquity in igneous rocks, zircon has been used as a proxy for magma crystallisation, crust production, and even crustal composition (Condie et al., 2009; Cawood et al., 2013; Parman, 2015; Lee et al., 2016).
View in article
Condie, K.C., Aster, R.C. (2010) Episodic zircon age spectra of orogenic granitoids: The supercontinent connection and continental growth. Precambrian Research 180, 227–236.
Show in context As peaks in global zircon age spectra are often interpreted as times of increased global magmatic activity, correlated with the plate tectonic Wilson cycle (e.g., Condie and Aster, 2010), the corrected age spectrum may imply a more steady-state supercontinent cycle with similar maxima in magmatic activity to ∼3 Ga, or (depending on the strength of preservation bias) even before.
View in article
Condie, K.C., Belousova, E., Griffin, W.L., Sircombe, K.N. (2009) Granitoid events in space and time: Constraints from igneous and detrital zircon age spectra. Gondwana Research 15, 228–242.
Show in contextGiven its ubiquity in igneous rocks, zircon has been used as a proxy for magma crystallisation, crust production, and even crustal composition (Condie et al., 2009; Cawood et al., 2013; Parman, 2015; Lee et al., 2016).
View in article
de Wit, M.J., Ashwal, L.D. (1997) Greenstone belts. Oxford University Press, Oxford.
Show in context This inequality between Archean mafic and felsic zircon abundance is exacerbated when considering magmas that do not fully crystallise, due to the greatly delayed zircon saturation of Archean mafic magmas (Fig. 1c) – an effect that would be further compounded by the apparent prevalence of volcanic lithologies in the Archean mafic record (e.g., de Wit and Ashwal, 1997).
View in article
Dhuime, B., Hawkesworth, C.J., Cawood, P.A., Storey, C.D. (2012) A Change in the Geodynamics of Continental Growth 3 Billion Years Ago. Science 335, 1334–1336.
Show in context While the above considerations are applicable in principle to zircon-based crustal growth models such as those of Belousova et al. (2010) or Dhuime et al. (2012), a simple correction factor as in Figure 3b alone is likely insufficient.
View in article
Ehmann, W.D., Chyi, L.L., Garg, A.N., Ali, M.Z. (1979) The distribution of zirconium and hafnium in terrestrial rocks, meteorites and the moon. Physics and Chemistry of the Earth 11, 247–259.
Show in context Consistent with this expectation, lunar anorthosites contain only 0.1–0.5 ppm zirconium (e.g., several hundred times lower than an average Archean basalt), offset by zirconium enrichments up to 2000 ppm in complementary KREEP basalts (Ehmann et al., 1979).
View in article
GERM (2013) Geochemical Earth Reference Model Partition Coefficient Database. http://www.earthref.org/KDD/
Show in context Consequently, to ensure accurate zircon saturation calculations, mineral-specific partition coefficients from the Geochemical Earth Reference Model database (GERM, 2013) were used when calculating melt Zr concentrations at each temperature step of each alphaMELTS simulation.
View in article
Ghiorso, M.S., Hirschmann, M.M., Reiners, P.W., Kress, V.C.III (2002) The pMELTS: A revision of MELTS for improved calculation of phase relations and major element partitioning related to partial melting of the mantle to 3 GPa. Geochemistry Geophysics Geosystems 3, 1–36.
Show in context Accordingly, in order to examine the effects of temporal variations in magma composition throughout Earth history on zircon saturation behaviour, we combine zircon saturation calculations with alphaMELTS (Ghiorso et al., 2002; Smith and Asimow, 2005) major element simulations on 52,300 whole rock compositions spanning the preserved rock record from modern to Archean.
View in article
Harrison, T.M. (2009) The Hadean Crust: Evidence from ¿4 Ga Zircons. Annual Review of Earth and Planetary Sciences 37, 479–505.
Show in context Zircons constitute the oldest known terrestrial material, providing a glimpse of Earth in the Hadean Eon which has been argued to reveal a remarkably modern environment, complete with liquid water (Mojzsis et al., 2001; Wilde et al., 2001) and felsic crust (Harrison, 2009).
View in article
Harrison, T.M., Watson, E.B., Aikman, A.B. (2007) Temperature spectra of zircon crystallization in plutonic rocks. Geology 35, 635.
Show in contextEven within a closed system, magma composition (including M and [Zr]melt) varies systematically throughout crystallisation as a function of pressure, temperature, and melt fraction, such that a single bulk zircon saturation temperature is insufficient to characterise the zircon saturation behaviour of simple igneous systems (e.g., Harrison et al., 2007).
View in article
Kamber, B.S., Whitehouse, M., Bolhar, R., Moorbath, S. (2005) Volcanic resurfacing and the early terrestrial crust: Zircon U–Pb and REE constraints from the Isua Greenstone Belt, southern West Greenland. Earth and Planetary Science Letters 240, 276–290.
Show in context Delayed zircon saturation in Archean lithologies should result in an even more pronounced dearth of zircons in the Archean volcanic record for magmas of any given silica content consistent with the observations in Eoarchean volcaniclastic metasediments, e.g., Kamber et al. (2005).
View in article
Keller, C.B., Schoene, B. (2012) Statistical geochemistry reveals disruption in secular lithospheric evolution about 2.5Gyr ago. Nature 485, 490– 493.
Show in contextHowever, on sufficiently long geologic timescales, decreasing mantle potential temperature from the early Earth to the present is reflected in systematic variations in average magma composition, including increasing abundance of incompatible elements such as Zr (Keller and Schoene, 2012).
View in article
Finally, to obtain temporal trends, the results of zircon saturation simulations were subjected to weighted bootstrap re-sampling following the approach of Keller and Schoene (2012), to calculate accurate estimates of the mean and standard error of the mean for each independent variable of interest.
View in article
These changes are a consequence of secular mantle cooling, where lower average mantle melting extent has led to increased average concentrations of incompatible elements such as Zr (Keller and Schoene, 2012), and generally lower M values due to lower Ca and higher Al abundance.
View in article
However, proposed scenarios of constant or decreasing crustal thickness (e.g., Keller and Schoene, 2012) and constant or increasing magma water content from the Archean to the present would, if anything, accentuate the trends observed in Figure 1.
View in article
Keller, C.B., Schoene, B., Barboni, M., Samperton, K.M., Husson, J.M. (2015) Volcanic–plutonic parity and the differentiation of the continental crust. Nature 523, 301–307.
Show in context Consequently, in drier or deeper magmas, most silicate minerals will crystallise early relative to zircon (Keller et al., 2015); such magmas will be more likely to crystallise fully to the solidus without ever reaching zircon saturation.
View in article
Given that basalts display the greatest delay in zircon saturation and are substantially over-represented in the volcanic record (Keller et al., 2015), the effect of eruptive quenching on zircon saturation will be most noticeable in the mafic record.
View in article
Lee, C.-T.A., Yeung, L.Y., McKenzie, N.R., Yokoyama, Y., Ozaki, K., Lenardic, A. (2016) Two-step rise of atmospheric oxygen linked to the growth of continents. Nature Geoscience 9, 417–424.
Show in context Given its ubiquity in igneous rocks, zircon has been used as a proxy for magma crystallisation, crust production, and even crustal composition (Condie et al., 2009; Cawood et al., 2013; Parman, 2015; Lee et al., 2016).
View in article
Mojzsis, S.J., Harrison, T.M., Pidgeon, R.T. (2001) Oxygen-isotope evidence from ancient zircons for liquid water at the Earth’s surface 4,300 Myr ago. Nature 409, 178–181.
Show in context Zircons constitute the oldest known terrestrial material, providing a glimpse of Earth in the Hadean Eon which has been argued to reveal a remarkably modern environment, complete with liquid water (Mojzsis et al., 2001; Wilde et al., 2001) and felsic crust (Harrison, 2009).
View in article
Parman, S.W. (2015) Time-lapse zirconography: Imaging punctuated continental evolution. Geochemical Perspectives Letters 1, 43–52.
Show in context Given its ubiquity in igneous rocks, zircon has been used as a proxy for magma crystallisation, crust production, and even crustal composition (Condie et al., 2009; Cawood et al., 2013; Parman, 2015; Lee et al., 2016).
View in article
Pearson, D.G., Parman, S.W., Nowell, G.M. (2007) A link between large mantle melting events and continent growth seen in osmium isotopes. Nature 449, 202–205.
Show in context The zircon abundance correction increases the magmatic significance of the Archean and Proterozoic zircon record, and appears to improve the correspondence in magnitude between temporally correlated zircon abundance maxima and mantle depletion events (e.g., Pearson et al., 2007).
View in article
Schmitt, A.K. (2011) Uranium Series Accessory Crystal Dating of Magmatic Processes. Annual Review of Earth and Planetary Sciences 39, 321–349.
Show in context This trinity of properties has made zircon into a standard mineral tracer of geologic time, resolving timescales from Gyr to kyr through the related U-Th/Pb and U-series geochronometers (e.g., Schmitt, 2011; Schoene, 2014).
View in article
Schoene, B. (2014) 4.10 U–Th–Pb Geochronology. In: Rudnick, R.L. (Ed.) Treatise on Geochemistry Volume 4: The Crust. Second edition. Elsevier, Amsterdam, 341–378.
Show in contextThis trinity of properties has made zircon into a standard mineral tracer of geologic time, resolving timescales from Gyr to kyr through the related U-Th/Pb and U-series geochronometers (e.g., Schmitt, 2011; Schoene, 2014).
View in article
Moreover, due to the high closure temperatures of the U-Th/Pb and U-series systems, ages from these geochronometers exclusively date zircon crystallisation (Schoene, 2014), which need not coincide with the crystallisation of other silicate minerals.
View in article
Smith, P.M., Asimow, P.D. (2005) Adiabat 1ph: A new public front-end to the MELTS, pMELTS, and pHMELTS models. Geochemistry Geophysics Geosystems 6, 1–8.
Show in contextAccordingly, in order to examine the effects of temporal variations in magma composition throughout Earth history on zircon saturation behaviour, we combine zircon saturation calculations with alphaMELTS (Ghiorso et al., 2002; Smith and Asimow, 2005) major element simulations on 52,300 whole rock compositions spanning the preserved rock record from modern to Archean.
View in article
Voice, P.J., Kowalewski, M., Eriksson, K.A. (2011) Quantifying the Timing and Rate of Crustal Evolution: Global Compilation of Radiometrically Dated Detrital Zircon Grains. The Journal of Geology 119, 109–126.
Show in context The impact of this trend on preserved zircon age spectra is shown in Figure 3a, which illustrates how the zircon age spectrum of Voice et al. (2011) would differ if magmas throughout Earth history had crystallised zircon at present-day rates, for a range of assumed model conditions.
View in article
Figure 3 The effect of applying a relative zircon abundance correction (normalising to constant magma zircon productivity) to the detrital zircon age spectrum of Voice et al. (2011) for varying crystallisation conditions.
View in article
Watson, E.B., Harrison, T.M. (1983) Zircon saturation revisited: temperature and composition effects in a variety of crustal magma types. Earth and Planetary Science Letters 64, 295–304.
Show in context The temperature Tsat at which zircon saturates in an igneous magma can be accurately predicted by an empirical equation of the form 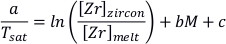where a, b, and c are constants, [Zr] is zirconium concentration, and M is a compositional measure of magma polymerisation defined on a molar basis as 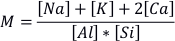(Watson and Harrison, 1983; Boehnke et al., 2013).
View in article
Wilde, S.A., Valley, J.W., Peck, W.H., Graham, C.M. (2001) Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago. Nature 409, 175–178.
Show in contextZircons constitute the oldest known terrestrial material, providing a glimpse of Earth in the Hadean Eon which has been argued to reveal a remarkably modern environment, complete with liquid water (Mojzsis et al., 2001; Wilde et al., 2001) and felsic crust (Harrison, 2009).
View in article
top
Supplementary Information
Zircon Saturation
In order to quantify the effects of changing magma composition on zircon abundance throughout Earth history, we calculated the expected mass of zircon saturated per unit mass of rock for 52,300 igneous whole rock compositions with defined major element and Zr contents from the dataset of Keller and Schoene (2012), integrating alphaMELTS equilibrium crystallisation simulations with zirconium partitioning calculations and the zircon saturation thermometer of Boehnke et al. (2013). For each whole rock composition, a pMELTS-mode alphaMELTS (Ghiorso et al., 2002; Asimow et al., 2004; Smith and Asimow, 2005) isobaric batch equilibrium crystallisation simulation was run from the liquidus to the solidus in 10 °C increments, recording the composition of the melt and all mineral phase proportions at each crystallisation step. At each step, the zircon saturation state was assessed by calculating the concentration of zirconium in the melt in the absence of zircon using the reported mineral phase proportions along with GERM mineral/melt Zr partition coefficients for each phase present, and comparing that to the concentration of zirconium required to saturate zircon at that temperature and major element composition using the equations of Boehnke et al. (2013). From these concentrations along with the remaining melt fraction, we calculate the total mass of extant zircon (if any) at each temperature step, as well as the differential zircon growth (if any) for each cooling increment. As discussed in the text, full simulations for each whole rock sample were conducted at a range of P, H2O conditions in order to quantify the effect of crystallisation pressure and water content on total mass of zircon saturated. While all simulations were run with an initial oxygen fugacity one log unit above the fayalite–magnetite–quartz redox buffer, compared to changes in crystallisation pressure or magma water content, magma redox state has negligible effect on melt zirconium content during equilibrium crystallisation.
Following these simulations, a resultant dataset recording the total mass of zircon saturated by the end of crystallisation for each whole rock sample at a given set of P, H2O conditions was then subjected to the weighted bootstrap resampling procedure of Keller and Schoene (2012) (with location, age, and age uncertainty as reported for each sample in the dataset) in order to evaluate the variation in average zircon abundance throughout the preserved rock record (e.g., Fig. 1). Finally, an intermediate set of P, H2O conditions (6 kbar, 3 wt. % H2O) were chosen to illustrate in more detail the typical consequences of lower Archean zirconium content, including delayed and diminished zircon saturation throughout the crystallisation process (Fig. 1c) and particularly diminished zircon saturation in mafic lithologies (Fig. 2).
Qualitatively, the effect of in situ magmatic differentiation is to drive up zirconium concentration in the residual melt, while at the same time reducing the minimum zirconium concentration required to saturate zircon due to declining temperature and M (Fig. S-1). Zircon saturation occurs when the two trends intersect, resulting in earlier saturation and higher saturation temperatures than in a bulk crystallisation model where melt evolution is ignored. Consequently, as seen in Figure S-2, corrected saturation temperatures universally exceed bulk saturation temperatures, particularly for samples which successfully saturate zircon. Similarly, corrected zircon saturation temperatures also necessarily exceed average zircon crystallisation temperatures for the same sample, though to a lesser degree.
Figure S-1 Zirconium evolution and the point of zircon saturation during a crystallisation simulation for a single whole rock composition, in this case a basaltic andesite composition. Zirconium concentration in the melt increases during differentiation as a generally incompatible element, while both temperature and M-value decrease with increasing crystallinity, decreasing the zirconium concentration required to saturate zircon.
Figure S-2 The relationship between bulk zircon saturation temperatures, corrected zircon saturation temperatures, and average zircon crystallisation temperatures during closed system equilibrium crystallisation for 52,300 whole rock compositions. Bulk saturation temperature is the result of applying the equation of Boehnke et al. (2013) directly to each whole rock composition. (a) Corrected zircon saturation temperature adjusts for differentiation during in situ crystallisation, resulting in consistently higher saturation temperatures relative to bulk saturation temperature, as observed in panel. For samples that do not ever saturate zircon, the highest saturation temperature of any differentiated melt is reported. (b) For samples which do saturate zircon, average zircon crystallisation temperature is the weighted average of the zircon crystallisation temperature distribution, resulting in temperatures closely correlated with, but necessarily colder than, the adjusted zircon saturation temperature. While not highly sensitive to pressure or water content, the values shown here are calculated for shallow, water saturated conditions (2 kbar and 4 wt. % H2O).
While slightly counterintuitive, the effect of high crystallisation pressure or low magma water content to decrease the total mass of zircon saturated is ultimately related to zirconium partitioning in silicate mineral phases other than zircon. Decreasing water content or increasing crystallisation pressure increases the temperature at which most silicate minerals begin to crystallise, but has little or no effect on zircon saturation temperature, thus moving silicate crystallisation forward relative to zircon saturation, or (equivalently) delaying zircon saturation as a function of percent crystallinity. While zirconium is generally incompatible in major rock-forming minerals, it is only slightly incompatible (or even approaches compatibility) in a range of important major and minor rock-forming minerals, and increases in compatibility as a function of melt SiO2 (Fig. S-3) with the net result that bulk solid/melt Zr partition coefficients for relevant mineral assemblages are typically greater than 0.05 and may exceed 0.2. Consequently, delaying zircon saturation may dramatically limit the amount of Zr available to form zircon, particularly in the case of gradual closed system crystallisation that approaches equilibrium partitioning. For example, if zircon saturation can be delayed until a bulk magma has reached 1 % melt remaining, even with a Kd of 0.1 (ten times greater zirconium concentration in the melt), the solid still contains roughly ten times more total zirconium than the remaining melt due to the 99-fold advantage of the solid in the total mass balance, and at most only 1/10th of the total zirconium is available at this point to crystallise zircon. This effect is illustrated in Figure S-3b for a range of potential bulk solid/melt partition coefficients. This effect is compounded in the event that the residual melt from bulk crystallisation of a given magma tends towards peralkaline compositions (as is not uncommon) due to the high zircon solubility of peralkaline magmas, which is sufficiently extreme that, for a range of expected crystallisation paths, “once zircon becomes unstable due to [an] increase in peralkalinity, the melt can never regain zircon saturation by continued feldspar crystallization” (Watson, 1979). As a result, delaying zircon saturation tends to markedly reduce the total mass of zircon saturation even in the absence of eruptive quenching.
All data and source code is freely available at https://github.com/brenhinkeller/meltstzirc.
Figure S-3 Zirconium partitioning. (a) Zirconium mineral/melt partition coefficients for several minerals with non-negligible zirconium compatibility. Partition coefficients shown are averages of GERM partition coefficient data fit as a function of melt SiO2. Uncertainties are omitted for visibility. (b) The proportion of the total zirconium budget partitioned into the solid at equilibrium as a function of remaining melt percent and mineral/melt partition coefficient.
Applications to Magma Volume and Crustal Growth
A zircon abundance correction factor as a function of crystallisation age (i.e. a scaling from zircon abundance to magma or crust volume) as in Figure 3b may be calculated by taking the inverse of the zircon abundance curve (Fig. 1b) and standardising to a value of 1 at the present. This correction may in principle be extended to zircon Hf model ages based on the crystallisation age of zircons with a given model age, and thence to crustal growth models. However, as discussed in the text, a single correction factor is likely insufficient to correct fully a zircon-based integrated crustal growth curve due to uncertainties regarding initial crustal volume and crustal return flux to the mantle via processes and lithologies that (for reasons of zircon stability and crystallisation systematics) do not leave a clear record in the crustal zircon archive.
To show the practical impact of such uncertainties, Figure S-4 illustrates how the crustal growth curve of Dhuime et al. (2012) might be altered in a range of plausible scenarios. In particular, the initial volume of primary crust circa 4.5 Ga is poorly bounded, considering the possibility for a nearly zirconium-free primary crust, analogous to the anorthosite flotation cumulate of the lunar highlands. The lunar anorthosite highlands are 60–100 km thick and cover a majority of the lunar surface (presumably all, at formation), with the net result that the lunar crust comprises 12 % of the volume of the moon (Taylor, 1989). The maximum thickness of an equivalent terrestrial floatation crust would be limited by the maximum pressure of feldspar stability considering terrestrial gravity, but even a comparatively modest ∼20 km thick global flotation crust would represent roughly twice the modern volume of continental crust. Absent an assumption of zero initial cumulate crust, the slope of the crustal volume curve is poorly constrained by the zircon record. There is no requirement from zircon geochemistry or age spectra that the mass flux from the mantle to the crust should exceed that from the crust to the mantle, and thus no requirement that net crustal growth rate should be positive. While intra-crustal reworking may be estimated from the continental zircon record (e.g., Belousova et al., 2010; Dhuime et al., 2012), crustal destruction by recycling to the mantle is not similarly constrained, and this mantle recycling term need not be small. Isotopic estimates suggest that crustal recycling to the mantle should consume roughly 0.35 crustal volumes per Gyr, or the entire present-day crustal volume in less than 3 Gyr (DePaolo, 1983). Figure S-4 illustrates several potential scenarios ranging from zero to twenty kilometres of primary crust and various functional forms for the recycling rate. However, all illustrated recycling rates are monotonic, which need not be the case; instead, it is entirely possible that maxima in crustal destruction match those in crustal production (e.g., Fig. 3a), such that episodic peaks in crust production may or may not result in episodes of net crustal growth. We conclude that both the initial boundary condition and subsequent evolution of the crustal volume curve may vary widely, leading to substantial uncertainty in crustal volume curves.
Figure S-4 A selection of possible crustal growth curves with varying initial boundary conditions (no crust, 5, 10, and 20 km thick primordial anorthosite floatation crust) and functional form of the recycling term (none, linear, and exponential with 0.7 or 1.4 Gyr e-folding time 1/λ). Exponential recycling rates are considered based on the possibility that crustal recycling rate may have been faster in the past as a direct and indirect result of higher mantle potential temperature.
Supplementary Information References
Belousova, E., Kostitsyn, Y., Griffin, W.L., Begg, G.C., O’Reilly, S.Y., Pearson, N.J. (2010) The growth of the continental crust: Constraints from zircon Hf-isotope data. LITHOS 119, 457–466.
Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
DePaolo, D.J. (1983) The mean life of continents: Estimates of continent recycling rates from Nd and Hf isotopic data and implications for mantle structure. Geophysical Research Letters 10, 705–708.
Dhuime, B., Hawkesworth, C.J., Cawood, P.A., Storey, C.D. (2012) A Change in the Geodynamics of Continental Growth 3 Billion Years Ago. Science 335, 1334–1336.
Ghiorso, M.S., Hirschmann, M.M., Reiners, P.W., Kress, V.C.III (2002) The pMELTS: A revision of MELTS for improved calculation of phase relations and major element partitioning related to partial melting of the mantle to 3 GPa. Geochemistry Geophysics Geosystems 3, 1–36.
Keller, C.B., Schoene, B. (2012) Statistical geochemistry reveals disruption in secular lithospheric evolution about 2.5 Gyr ago. Nature 485, 490– 493.
Smith, P.M., Asimow, P.D. (2005) Adiabat 1ph: A new public front-end to the MELTS, pMELTS, and pHMELTS models. Geochemistry Geophysics Geosystems 6, 1–8.
Taylor, S.R. (1989) Growth of planetary crusts. Tectonophysics 161, 147–156.
Watson, E.B. (1979) Zircon saturation in felsic liquids: Experimental results and applications to trace element geochemistry. Contributions to Mineralogy and Petrology 70, 407–419.
Figures and Tables
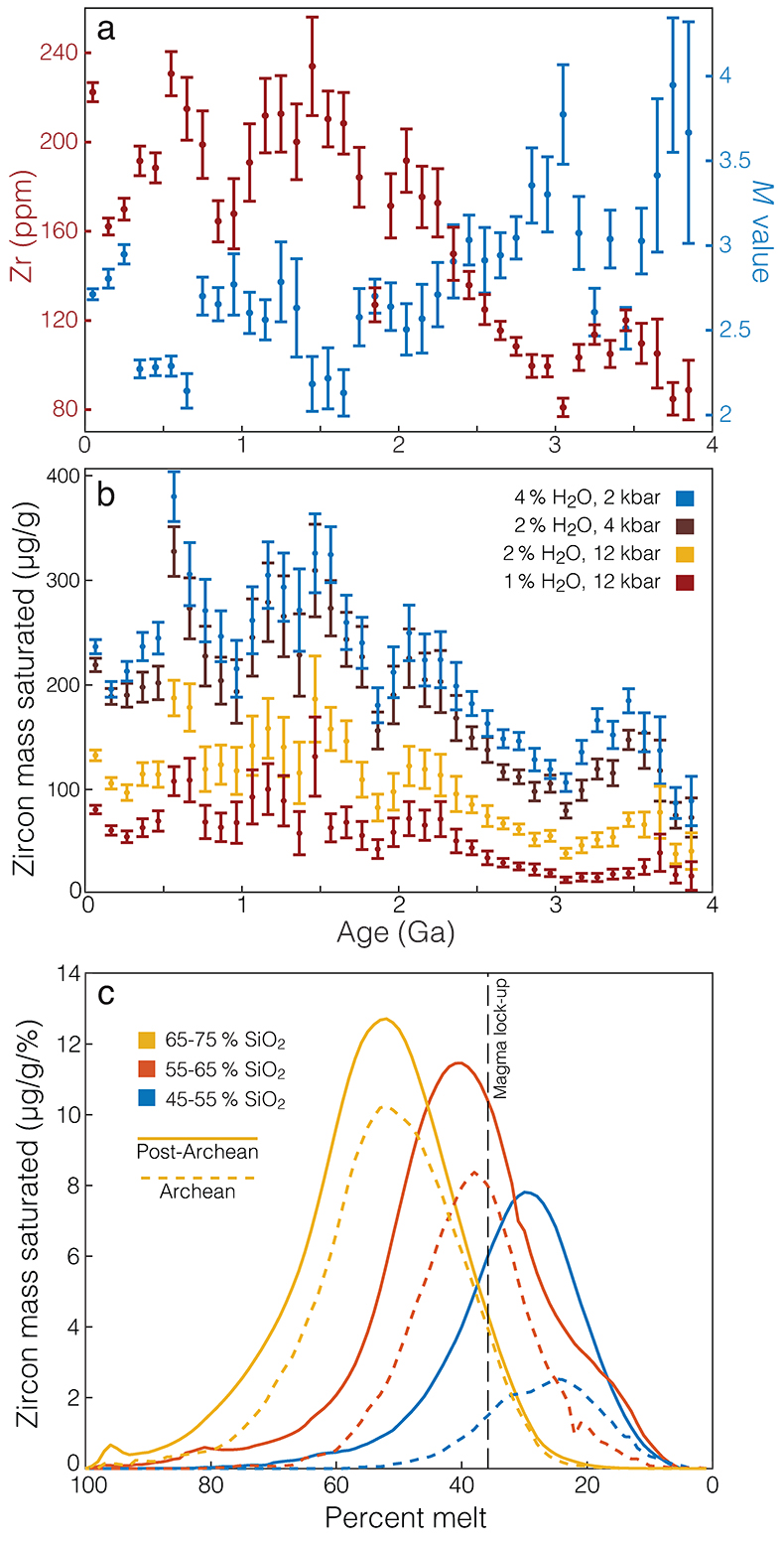
Figure 1 (a) Average zirconium and M value throughout the preserved rock record for continental igneous rocks with 40–80 % SiO2. (b) Calculated average zircon concentration (micrograms of zircon per gram of whole rock) as a function of time, under a range of possible crystallisation conditions. (c) Zircon saturation distributions during magma crystallisation as a function of percent melt for varying silica ranges, calculated at 6 kilobar and 3 wt. % H2O. Relative zircon abundance is reported as micrograms of zircon saturated per gram of magma per percentage-point decrease in residual melt fraction. All uncertainties are two standard error of the mean.
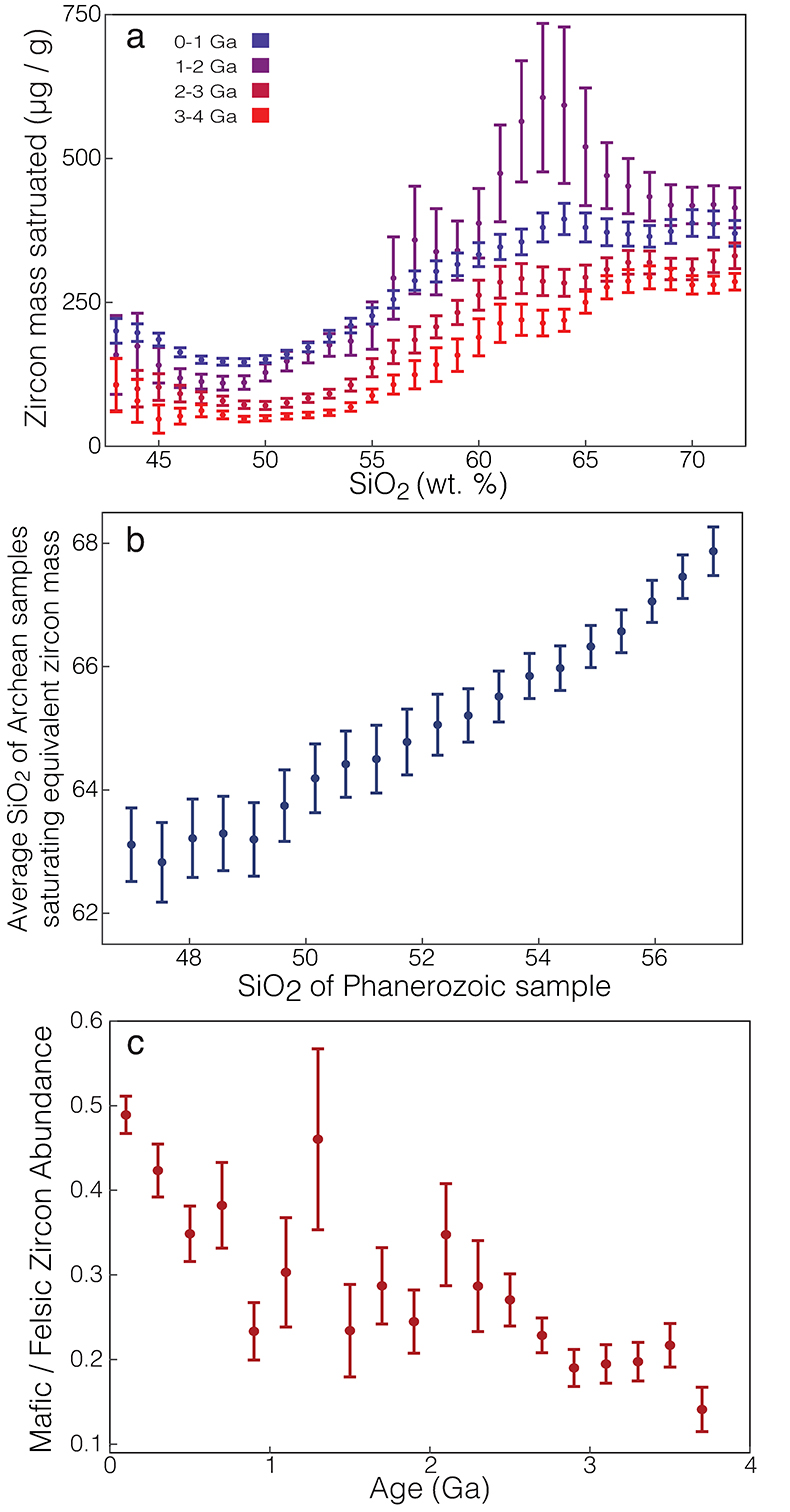
Figure 2 (a) Temporal variability in the distribution of zircon between igneous rocks of different silica contents, calculated at 6 kilobar and 3 wt. % H2O. (a) Temporal variation in relative zircon abundance as a function of silica. (b) Line of silica equivalence between Archean and Phanerozoic samples (the silica contents required to saturate the same mass of zircon in Archean and Phanerozoic magmas). (c) The mass of zircon saturated per mass of mafic magma (43–53 % SiO2) relative to that saturated in an equivalent mass of coeval felsic magma (63–73 % SiO2). The likelihood of saturating zircon in mafic lithologies was dramatically lower (by a factor of nearly 5) in the earliest Archean than it is today. All uncertainties are two standard error of the mean.
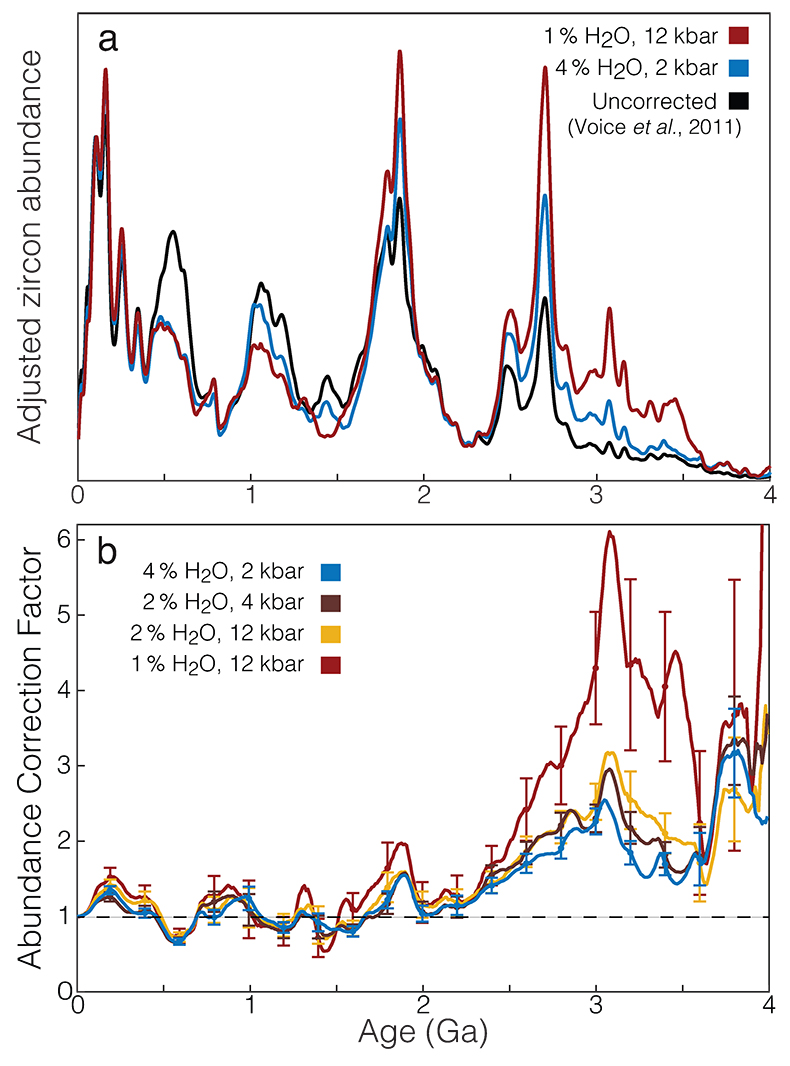
Figure 3 (a) The effect of applying a relative zircon abundance correction (normalising to constant magma zircon productivity) to the detrital zircon age spectrum of Voice et al. (2011)
Voice, P.J., Kowalewski, M., Eriksson, K.A. (2011) Quantifying the Timing and Rate of Crustal Evolution: Global Compilation of Radiometrically Dated Detrital Zircon Grains. The Journal of Geology 119, 109–126.
for varying crystallisation conditions. (b) The average mass of magma throughout Earth history required to produce the same mass of zircon as a unit mass of average present-day magma.Back to article
Supplementary Figures and Tables
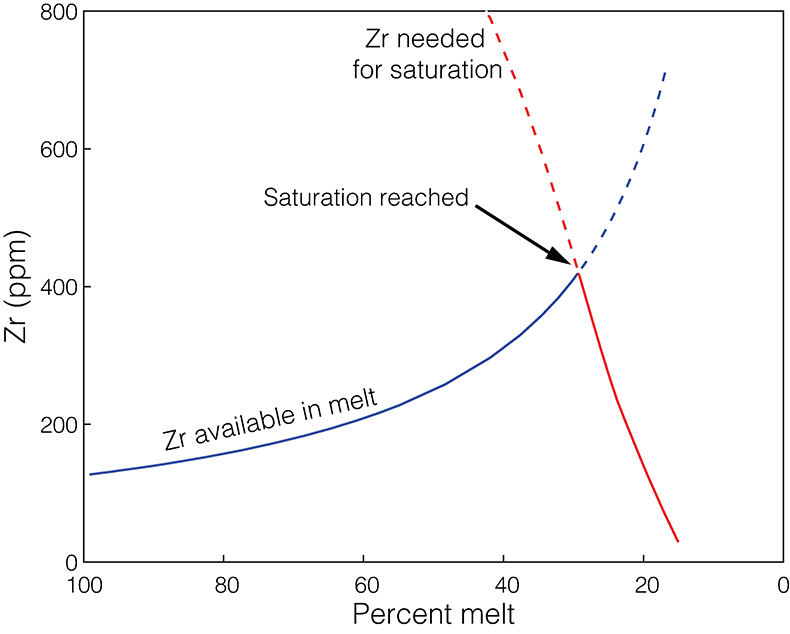
Figure S-1 Zirconium evolution and the point of zircon saturation during a crystallisation simulation for a single whole rock composition, in this case a basaltic andesite composition. Zirconium concentration in the melt increases during differentiation as a generally incompatible element, while both temperature and M-value decrease with increasing crystallinity, decreasing the zirconium concentration required to saturate zircon.
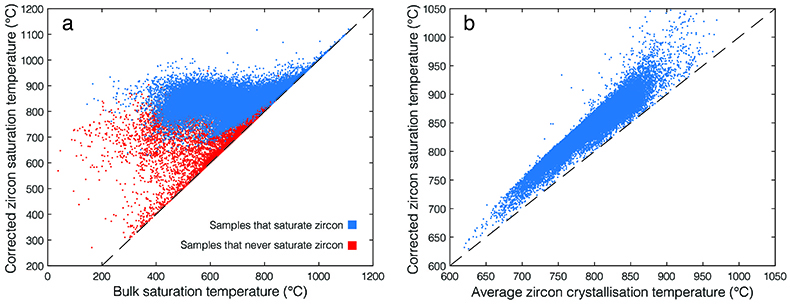
Figure S-2 The relationship between bulk zircon saturation temperatures, corrected zircon saturation temperatures, and average zircon crystallisation temperatures during closed system equilibrium crystallisation for 52,300 whole rock compositions. Bulk saturation temperature is the result of applying the equation of Boehnke et al. (2013) directly to each whole rock composition. (a) Corrected zircon saturation temperature adjusts for differentiation during in situ crystallisation, resulting in consistently higher saturation temperatures relative to bulk saturation temperature, as observed in panel. For samples that do not ever saturate zircon, the highest saturation temperature of any differentiated melt is reported. (b) For samples which do saturate zircon, average zircon crystallisation temperature is the weighted average of the zircon crystallisation temperature distribution, resulting in temperatures closely correlated with, but necessarily colder than, the adjusted zircon saturation temperature. While not highly sensitive to pressure or water content, the values shown here are calculated for shallow, water saturated conditions (2 kbar and 4 wt. % H2O).
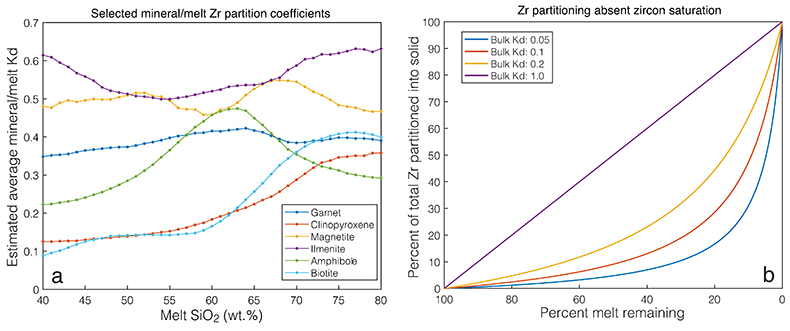
Figure S-3 Zirconium partitioning. (a) Zirconium mineral/melt partition coefficients for several minerals with non-negligible zirconium compatibility. Partition coefficients shown are averages of GERM partition coefficient data fit as a function of melt SiO2. Uncertainties are omitted for visibility. (b) The proportion of the total zirconium budget partitioned into the solid at equilibrium as a function of remaining melt percent and mineral/melt partition coefficient.
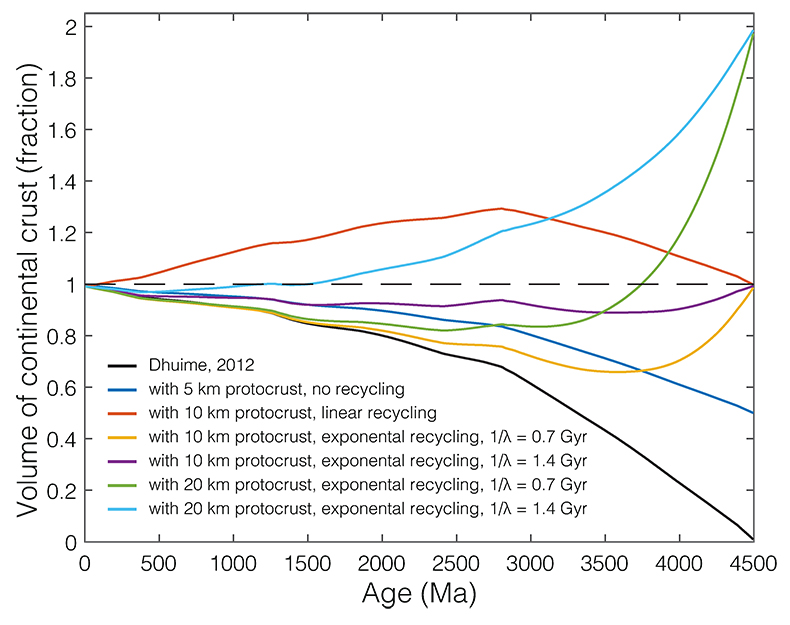
Figure S-4 A selection of possible crustal growth curves with varying initial boundary conditions (no crust, 5, 10, and 20 km thick primordial anorthosite floatation crust) and functional form of the recycling term (none, linear, and exponential with 0.7 or 1.4 Gyr e-folding time 1/λ). Exponential recycling rates are considered based on the possibility that crustal recycling rate may have been faster in the past as a direct and indirect result of higher mantle potential temperature.