Diffusional fractionation of helium isotopes in silicate melts
Affiliations | Corresponding Author | Cite as | Funding information
Published by the European Association of Geochemistry
under Creative Commons License CC BY-NC-ND 4.0
Keywords: diffusion, helium isotopes, molecular dynamics, machine learning
- Share this article
-
Article views:468Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Figures
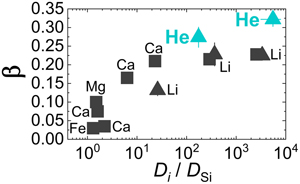
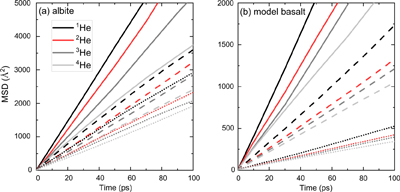 Figure 1 Mean square displacement (MSD) of He isotopes (1He, 2He, 3He, 4He) as a function of time in (a) albite and (b) model basalt melts at 3000 (solid lines), 2200 (dashed lines), and 1700 K (dotted lines) around zero pressure. | 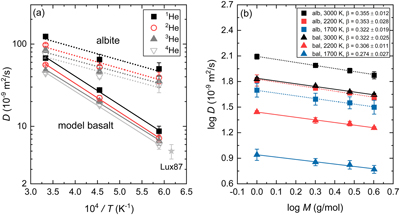 Figure 2 (a) Diffusion coefficients of He isotopes (1He, 2He, 3He, 4He) as a function of temperature in albite and model basalt melts around zero pressure. The experimental data (Lux87) for the diffusivity of He in a tholeiitic melt is from Lux (1987). (b) Log-log plot of the diffusivities of He isotopes in albite (alb) and model basalt (bal) melts as a function of isotopic mass at different temperatures around zero pressure. | 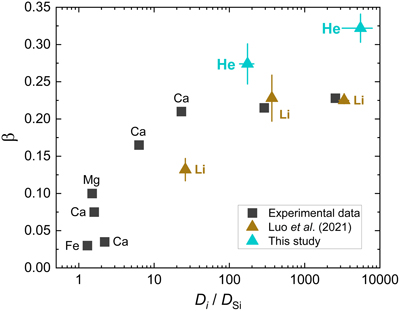 Figure 3 Relationship of β with solvent normalised diffusivity (Di/DSi). Experimental data is from Richter et al. (2003, 2009), Watkins et al. (2009, 2011), and Holycross et al. (2018). Computational results of Li at 1800 K are from Luo et al. (2021). All data shown here are for the relatively narrow temperature range 1623–1800 K, except one data point from Holycross et al. (2018). | 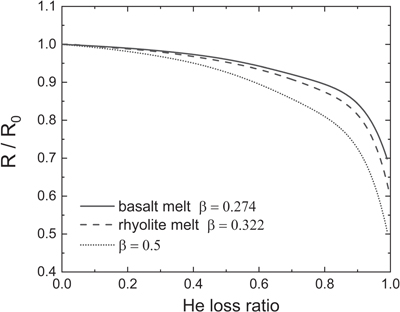 Figure 4 (3He/4He)/(3He/4He)0 as a function of He loss ratio for different β values. |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
top
Letter
Noble gases are known to be chemically inert, which means that their compositions were not altered by chemical or biological processes over the Earth’s history. Only physical processes such as diffusion, adsorption, or ion implantation may cause significant elemental and isotopic fractionations (Moreira, 2013
Moreira, M. (2013) Noble Gas Constraints on the Origin and Evolution of Earth’s Volatiles. Geochemical Perspectives 2, 229–230.
). The inert behaviour combined with the existence of both radiogenic and non-radiogenic isotopes for each noble gas provides powerful tools for constraining mantle degassing history and identifying long lived heterogeneities within the mantle (Behrens, 2010Behrens, H. (2010) Noble Gas Diffusion in Silicate Glasses and Melts. Reviews in Mineralogy and Geochemistry 72, 227–267.
; Moreira, 2013Moreira, M. (2013) Noble Gas Constraints on the Origin and Evolution of Earth’s Volatiles. Geochemical Perspectives 2, 229–230.
; Moreira and Kurz, 2013Moreira, M.A., Kurz, M.D. (2013) Noble Gases as Tracers of Mantle Processes and Magmatic Degassing. In: Burnard P. (Ed.) The Noble Gases as Geochemical Tracers. Advances in Isotope Geochemistry. First Edition, Springer-Verlag, Berlin, Heidelberg, 371–391.
). However, measured noble gas isotope ratios in mid-ocean ridge basalts (MORB) and oceanic island basalts (OIB) are often difficult to interpret due to possible fractionations that happen in magma degassing (Moreira and Kurz, 2013Moreira, M.A., Kurz, M.D. (2013) Noble Gases as Tracers of Mantle Processes and Magmatic Degassing. In: Burnard P. (Ed.) The Noble Gases as Geochemical Tracers. Advances in Isotope Geochemistry. First Edition, Springer-Verlag, Berlin, Heidelberg, 371–391.
).Magma degassing occurs in a closed or open system. The changes of noble gas isotope compositions during closed system degassing are determined by equilibrium isotope fractionation between noble gases dissolved in the melt and noble gases in the gas phase. In comparison, magma degassing in an open system may be diffusion controlled (Watson, 2017
Watson, E.B. (2017) Diffusive fractionation of volatiles and their isotopes during bubble growth in magmas. Contributions to Mineralogy and Petrology 172, 61.
) and diffusion can fractionate isotopes considerably even at magmatic temperatures (e.g., Richter et al., 1999Richter, F.M., Liang, Y., Davis, A.M. (1999) Isotope fractionation by diffusion in molten oxides. Geochimica et Cosmochimica Acta 63, 2853–2861.
; Watkins et al., 2017Watkins, J.M., DePaolo, D.J., Watson, E.B. (2017) Kinetic Fractionation of Non-Traditional Stable Isotopes by Diffusion and Crystal Growth Reactions. Non-Traditional Stable Isotopes 82, 85–125.
). Diffusional separation of isotopes can be expressed as (Richter et al., 1999Richter, F.M., Liang, Y., Davis, A.M. (1999) Isotope fractionation by diffusion in molten oxides. Geochimica et Cosmochimica Acta 63, 2853–2861.
):Eq. 1
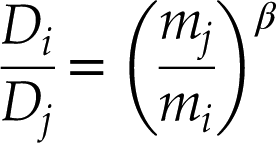
where Di and Dj are diffusion coefficients of two isotopes whose masses are mi and mj and β is a dimensionless empirical parameter. The knowledge of β for noble gases in silicate melts is essential to interpret noble gas isotope ratios. However, no experiments have studied diffusional fractionation of noble gas isotopes in high temperature silicate melts. The results from previous diffusion experiments using silicate glasses (Shelby, 1971
Shelby, J.E. (1971) Diffusion of Helium isotopes in vitreous silica. Physical Review B 4, 2681–2686.
; Trull and Kurz, 1999Trull, T.W., Kurz, M.D. (1999) Isotopic fractionation accompanying helium diffusion in basaltic glass. Journal of Molecular Structure 485, 555–567.
) may not be extrapolated to the cases in silicate melts, although silicate glasses are widely regarded as proper structural analogues of silicate melts. The reason is that the dynamics of silicate networks in high temperature melts help open and close paths for noble gas diffusion, which may play a key role in determining diffusional isotope fractionation (Behrens, 2010Behrens, H. (2010) Noble Gas Diffusion in Silicate Glasses and Melts. Reviews in Mineralogy and Geochemistry 72, 227–267.
; Watkins et al., 2017Watkins, J.M., DePaolo, D.J., Watson, E.B. (2017) Kinetic Fractionation of Non-Traditional Stable Isotopes by Diffusion and Crystal Growth Reactions. Non-Traditional Stable Isotopes 82, 85–125.
). Additionally, it is known that the diffusivities of noble gases show non-Arrhenius behaviour around the glass transition temperature (Behrens, 2010Behrens, H. (2010) Noble Gas Diffusion in Silicate Glasses and Melts. Reviews in Mineralogy and Geochemistry 72, 227–267.
; Amalberti et al., 2016Amalberti, J., Burnard, P., Laporte, D., Tissandier, L., Neuville, D.R. (2016) Multidiffusion mechanisms for noble gases (He, Ne, Ar) in silicate glasses and melts in the transition temperature domain: Implications for glass polymerization. Geochimica et Cosmochimica Acta 172, 107–126.
), which may imply a change in diffusion mechanism and thus influence diffusional isotope fractionation.First principles molecular dynamics (FPMD) simulations are reliable to calibrate β in liquids (Luo et al., 2020
Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2020) First-principles computation of diffusional Mg isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 290, 27–40.
), but the high computational cost makes them unsuitable to deal with trace elements (e.g., noble gases and Li). A recently developed technique called deep potential molecular dynamics (DPMD) simulations (Wang et al., 2018Wang, H., Zhang, L.F., Han, J.Q., E, W. (2018) DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Computer Physics Communications 228, 178–184.
; Zhang et al., 2018Zhang, L.F., Han, J.Q., Wang, H., Saidi, W., Car, R., E, W. (2018) End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. Advances of the Neural Information Processing Systems 31, 4441–4451.
), which is based on potentials trained by deep neural networks using ab initio data and is orders of magnitude faster than FPMD with comparable ab initio accuracy, has been successfully applied to predict β for Li in silicate melts (Luo et al., 2021Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2021) Deep neural network potentials for diffusional lithium isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 303, 38–50.
). Here we perform DPMD simulations to study diffusional He isotope fractionation in albite and model basalt melts at 3000, 2200, and 1700 K around zero pressure. The major technical improvement in this study is that the deep potential generator (DP-GEN) (Zhang et al., 2020Zhang, Y.Z., Wang, H.D., Chen, W.J., Zeng, J.Z., Zhang, L.F., Wang, H., E, W. (2020) DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Computer Physics Communications 253, 107206.
) is used to achieve a concurrent learning procedure and to obtain a representative training data set in a rigorous way (Supplementary Information).Albite and model basalt melts (excess Ca to compensate Fe) are close analogues of natural rhyolite and basalt melts, respectively. One He atom is added to the albite melt containing 8 NaAlSi3O8 (104 atoms) and the model basalt melt containing Ca9Mg6Al6Si18O60 (99 atoms), respectively. We conduct the simulations at 3000 K for 1 nanosecond (ns) with a time step of 0.5 femtosecond (fs) and at 2200 and 1700 K for 4 ns with a time step of 1.0 fs. Each simulation is repeated five times with different initial configurations. The accuracy of DPMD simulations is validated by comparing the predicted energies (Fig. S-1), forces (Fig. S-2), and radial distribution functions (Fig. S-3) with those calculated from FPMD simulations. To derive a reliable β from the linear fitting of logD vs. logM based on Equation 1, we use two pseudo-isotopes with masses M* = 1 and 2 g/mol, in addition to the two natural He isotopes (3He and 4He). The self diffusivities of the four He isotopes are calculated using the Einstein relation (Einstein, 1956
Einstein, A. (1956) Investigations on the Theory of Brownian Movement. First Edition, Dover, New York.
):Eq. 2
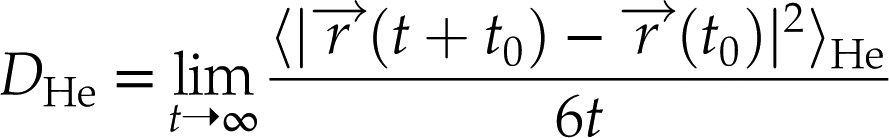
where
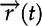represents the particle trajectories and 〈…〉He denotes average mean square displacement (MSD) over time from different time origins t0. The average value over the five independent simulations and the corresponding confidence interval (±2 s.e.) on the diffusivities are reported. The finite size effect on the diffusivities of He isotopes is insignificant within error after considering the correction relation proposed by Yeh and Hummer (Yeh and Hummer, 2004Yeh, I.-C., Hummer, G. (2004) System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. The Journal of Physical Chemistry B 108, 15873–15879.
).In Figure 1, linear MSD-time curves indicate that the diffusion of He isotopes was sampled well. All MSD curves for the four He isotopes at each condition are clearly separated. As suggested in previous studies (e.g., Bourg and Sposito, 2007
Bourg, I.C., Sposito, G. (2007) Molecular dynamics simulations of kinetic isotope fractionation during the diffusion of ionic species in liquid water. Geochimica et Cosmochimica Acta 71, 5583–5589.
; Luo et al., 2020Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2020) First-principles computation of diffusional Mg isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 290, 27–40.
), only the first part of MSD curves in the diffusive regime (9–10 picoseconds (ps), 20–40 ps, and 50–100 ps at 3000, 2200, and 1700 K, respectively) is used to approximate the infinite time limit in Equation 2. We find that He diffuses much faster in albite than in model basalt melts, consistent with the trend found in glasses (Behrens, 2010Behrens, H. (2010) Noble Gas Diffusion in Silicate Glasses and Melts. Reviews in Mineralogy and Geochemistry 72, 227–267.
). Calculated diffusion coefficients of He isotopes display a negative correlation with mass and a positive correlation with temperature in both albite and model basalt melts (Table S-1, Fig. 2a). The temperature dependence of diffusivities is fit to the Arrhenius relation:Eq. 3
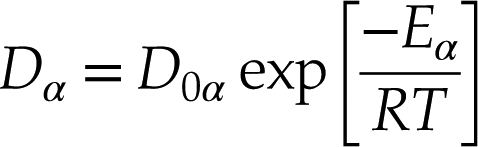
where α represents a He isotope. The predicted pre-exponential factor (D0α) and activation energy (Eα) appear to decrease with increasing isotopic mass of He (Fig. S-4). The predicted diffusivity for 4He in model basalt melt at 1623 K is 4.81 × 10−9 m2/s, which agrees well with the experimental value of 5 × 10−9 m2/s in a tholeiitic melt (Lux, 1987
Lux, G. (1987) The behavior of noble gases in silicate liquids-solution, diffusion, bubbles and surafce effects, with applications to natural samples. Geochimica et Cosmochimica Acta 51, 1549–1560.
) and the computational result from classical MD in a MORB melt (Guillot and Sator, 2012Guillot, B., Sator, N. (2012) Noble gases in high-pressure silicate liquids: A computer simulation study. Geochimica et Cosmochimica Acta 80, 51–69.
), although it is unclear why an experiment reported a much lower value of 0.28 × 10−9 m2/s in model basalt melt at 1673 K (Amalberti et al., 2018Amalberti, J., Burnard, P., Tissandier, L., Laporte, D. (2018) The diffusion coefficients of noble gases (He–Ar) in a synthetic basaltic liquid: One-dimensional diffusion experiments. Chemical Geology 480, 35–43.
). Eα for 4He in albite and model basalt melts are 27.9 ± 7.6 and 65.8 ± 2.4 kJ/mol, respectively. No experiments have reported activation energy for He diffusion in silicate melts. The experimental activation energies for He diffusion in albite and basalt glasses at much lower temperatures (398–673 K) are 31.7 (Shelby and Eagan, 1976Shelby, J.E., Eagan, R.J. (1976) Helium migration in sodium aluminosilicate glasses. Journal of the American Ceramic Society 59, 420–425.
) and 83 ± 4 kJ/mol (Kurz and Jenkins, 1981Kurz, M.D., Jenkins, W.J. (1981) The distribution of Helium in oceanic basalt glasses. Earth and Planetary Science Letters 53, 41–54.
), respectively. The smaller activation energies predicted by FPMD simulations compared to experimental results have been extensively reported (Karki et al., 2018Karki, B.B., Ghosh, D.B., Bajgain, S.K. (2018) Chapter 16 - Simulation of Silicate Melts Under Pressure. In: Kono, Y., Sanloup, C. (Eds.) Magmas Under Pressure. First Edition, Elsevier, Amsterdam, 419–453.
). The very different temperature ranges explored in simulations and experiments may account for the discrepancy. It is worth stressing that He diffusion in albite melt shows a small non-Arrhenius behaviour (Fig. 2a).Figure 1 Mean square displacement (MSD) of He isotopes (1He, 2He, 3He, 4He) as a function of time in (a) albite and (b) model basalt melts at 3000 (solid lines), 2200 (dashed lines), and 1700 K (dotted lines) around zero pressure.
Figure 2 (a) Diffusion coefficients of He isotopes (1He, 2He, 3He, 4He) as a function of temperature in albite and model basalt melts around zero pressure. The experimental data (Lux87) for the diffusivity of He in a tholeiitic melt is from Lux (1987)
Lux, G. (1987) The behavior of noble gases in silicate liquids-solution, diffusion, bubbles and surafce effects, with applications to natural samples. Geochimica et Cosmochimica Acta 51, 1549–1560.
. (b) Log-log plot of the diffusivities of He isotopes in albite (alb) and model basalt (bal) melts as a function of isotopic mass at different temperatures around zero pressure.The linear correlation of logD with logM in Figure 2b is consistent with the empirical Equation 1 proposed by Richter et al. (1999)
Richter, F.M., Liang, Y., Davis, A.M. (1999) Isotope fractionation by diffusion in molten oxides. Geochimica et Cosmochimica Acta 63, 2853–2861.
. The calculated β in albite melt decreases from 0.355 ± 0.012 at 3000 K to 0.322 ± 0.019 at 1700 K. In comparison, β in model basalt melt takes a smaller value from 0.322 ± 0.025 to 0.274 ± 0.027 over the same temperature range. The smaller β value in model basalt than in albite melt is the same as that observed in the case of Li, which makes sense as both He and Li diffuse faster in rhyolitic than in basaltic melt due to higher ionic porosity of rhyolitic melt. The decreasing trend of β with temperature in silicate melts around zero pressure has been reported in the simulations of diffusional Mg and Li isotope fractionation (Luo et al., 2020Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2020) First-principles computation of diffusional Mg isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 290, 27–40.
, 2021Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2021) Deep neural network potentials for diffusional lithium isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 303, 38–50.
). An assumed linear regression fit to β vs. T−1 yields relationships: β = (0.397 ± 0.017) − (0.012 ± 0.004) × 104/T in albite melt and β = (0.389 ± 0.021) − (0.019 ± 0.005) × 104/T in model basalt melt. The stronger temperature dependence of β for Li in model basalt than in albite melt is also observed here for He. Based on the predicted β values, a drop of temperature by 300 K (1700–1400 K in basaltic melt or 1400–1100 K in rhyolitic melt) results in a negligible decrease (∼0.7 %) of D3He/D4He value. Thus, we suggest that using the data at 1700 K, D3He/D4He values of 1.082 ± 0.008 in model basalt melt and 1.097 ± 0.006 in albite melt, are accurate enough when dealing with diffusional fractionation of He isotopes in natural silicate melts at shallow depths of the present day Earth.It has been proposed that β positively correlates with solvent normalised diffusivity (Di/DSi), implying that cations that are easier to decouple from the silicate matrix exhibit a larger diffusional isotope fractionation (Watkins et al., 2011
Watkins, J.M., DePaolo, D.J., Ryerson, F.J., Peterson, B.T. (2011) Influence of liquid structure on diffusive isotope separation in molten silicates and aqueous solutions. Geochimica et Cosmochimica Acta 75, 3103–3118.
, 2017Watkins, J.M., DePaolo, D.J., Watson, E.B. (2017) Kinetic Fractionation of Non-Traditional Stable Isotopes by Diffusion and Crystal Growth Reactions. Non-Traditional Stable Isotopes 82, 85–125.
). Note that Luo et al. (2020Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2020) First-principles computation of diffusional Mg isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 290, 27–40.
, 2021Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2021) Deep neural network potentials for diffusional lithium isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 303, 38–50.
) stressed that this positive correlation only works at a constant or narrowly defined temperature range as β in silicate melts is found to decrease with decreasing temperature while Di/DSi increases. The correlation of β for He with DHe/DSi at 1700 K broadly follows the previous positive trend (Fig. 3). The value of DHe/DSi is ∼5525 ± 2378 in albite melt, much larger than the value of ∼174 ± 37 in model basalt melt. However, it seems that the overall relationship between β and Di/DSi becomes less defined even at a narrow temperature range when data for different elements in different melt systems are considered (Fig. 3). This could be attributed to different extents of compositional dependence of both β and Di/DSi. More data are needed to further explore this issue.Figure 3 Relationship of β with solvent normalised diffusivity (Di/DSi). Experimental data is from Richter et al. (2003
Richter, F.M., Davis, A.M., DePaolo, D.J., Watson, E.B. (2003) Isotope fractionation by chemical diffusion between molten basalt and rhyolite. Geochimica et Cosmochimica Acta 67, 3905–3923.
, 2009Richter, F.M., Watson, E.B., Mendybaev, R., Dauphas, N., Georg, B., Watkins, J., Valley, J. (2009) Isotopic fractionation of the major elements of molten basalt by chemical and thermal diffusion. Geochimica et Cosmochimica Acta 73, 4250–4263.
), Watkins et al. (2009Watkins, J.M., DePaolo, D.J., Huber, C., Ryerson, F.J. (2009) Liquid composition-dependence of calcium isotope fractionation during diffusion in molten silicates. Geochimica et Cosmochimica Acta 73, 7341–7359.
, 2011Watkins, J.M., DePaolo, D.J., Ryerson, F.J., Peterson, B.T. (2011) Influence of liquid structure on diffusive isotope separation in molten silicates and aqueous solutions. Geochimica et Cosmochimica Acta 75, 3103–3118.
), and Holycross et al. (2018)Holycross, M.E., Watson, E.B., Richter, F.M., Villeneuve, J. (2018) Diffusive fractionation of Li isotopes in wet, highly silicic melts. Geochemical Perspectives Letters 6, 39–42.
. Computational results of Li at 1800 K are from Luo et al. (2021)Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2021) Deep neural network potentials for diffusional lithium isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 303, 38–50.
. All data shown here are for the relatively narrow temperature range 1623–1800 K, except one data point from Holycross et al. (2018)Holycross, M.E., Watson, E.B., Richter, F.M., Villeneuve, J. (2018) Diffusive fractionation of Li isotopes in wet, highly silicic melts. Geochemical Perspectives Letters 6, 39–42.
.Helium is the fastest diffusing species in natural silicate melts (except H2 which is easily oxidised) and there is a positive correlation between diffusivity and β at fixed temperatures. Thus, it is fair to say that the overall range of β for different elements in natural silicate melts is ∼0–0.32. The largest β value is given by He isotope diffusion in rhyolitic melt, which is still much lower than the value of 0.5 in the case of ideal gas. Given measured He isotope ratios of geological samples (rocks, minerals, glasses, or melt inclusions) that went through diffusive degassing at the magmatic stage, a smaller β value means that the samples must have lost more He than previously thought.
For example, reducing an initial 3He/4He ratio by 10 % requires 60 % gas loss for β equal to 0.5, but 73 % loss for β of 0.322 in rhyolite melt and 77 % loss for β of 0.274 in basalt melt (Fig. 4, Supplementary Information). Our reported β values are useful for quantitatively estimating He loss during magmatic degassing and trace back He concentration and isotope composition of magma source region.
Figure 4 (3He/4He)/(3He/4He)0 as a function of He loss ratio for different β values.
top
Acknowledgements
The research is supported by the Strategic Priority Research Program (B) of Chinese Academy of Sciences (XDB18010104) and National Science Foundation (EAR 1764140 and 2001074). High-performance computing resources were provided by Louisiana State University.
Editor: Anat Shahar
top
References
Amalberti, J., Burnard, P., Laporte, D., Tissandier, L., Neuville, D.R. (2016) Multidiffusion mechanisms for noble gases (He, Ne, Ar) in silicate glasses and melts in the transition temperature domain: Implications for glass polymerization. Geochimica et Cosmochimica Acta 172, 107–126.
Show in context Additionally, it is known that the diffusivities of noble gases show non-Arrhenius behaviour around the glass transition temperature (Behrens, 2010; Amalberti et al., 2016), which may imply a change in diffusion mechanism and thus influence diffusional isotope fractionation.
View in article
Amalberti, J., Burnard, P., Tissandier, L., Laporte, D. (2018) The diffusion coefficients of noble gases (He–Ar) in a synthetic basaltic liquid: One-dimensional diffusion experiments. Chemical Geology 480, 35–43.
Show in context The predicted diffusivity for 4He in model basalt melt at 1623 K is 4.81 × 10−9 m2/s, which agrees well with the experimental value of 5 × 10−9 m2/s in a tholeiitic melt (Lux, 1987) and the computational result from classical MD in a MORB melt (Guillot and Sator, 2012), although it is unclear why an experiment reported a much lower value of 0.28 × 10−9 m2/s in model basalt melt at 1673 K (Amalberti et al., 2018).
View in article
Behrens, H. (2010) Noble Gas Diffusion in Silicate Glasses and Melts. Reviews in Mineralogy and Geochemistry 72, 227–267.
Show in context The inert behaviour combined with the existence of both radiogenic and non-radiogenic isotopes for each noble gas provides powerful tools for constraining mantle degassing history and identifying long lived heterogeneities within the mantle (Behrens, 2010; Moreira, 2013; Moreira and Kurz, 2013).
View in article
The reason is that the dynamics of silicate networks in high temperature melts help open and close paths for noble gas diffusion, which may play a key role in determining diffusional isotope fractionation (Behrens, 2010; Watkins et al., 2017).
View in article
We find that He diffuses much faster in albite than in model basalt melts, consistent with the trend found in glasses (Behrens, 2010).
View in article
Additionally, it is known that the diffusivities of noble gases show non-Arrhenius behaviour around the glass transition temperature (Behrens, 2010; Amalberti et al., 2016), which may imply a change in diffusion mechanism and thus influence diffusional isotope fractionation.
View in article
Bourg, I.C., Sposito, G. (2007) Molecular dynamics simulations of kinetic isotope fractionation during the diffusion of ionic species in liquid water. Geochimica et Cosmochimica Acta 71, 5583–5589.
Show in context As suggested in previous studies (e.g., Bourg and Sposito, 2007; Luo et al., 2020), only the first part of MSD curves in the diffusive regime (9–10 picoseconds (ps), 20–40 ps, and 50–100 ps at 3000, 2200, and 1700 K, respectively) is used to approximate the infinite time limit in Equation 2.
View in article
Einstein, A. (1956) Investigations on the Theory of Brownian Movement. First Edition, Dover, New York.
Show in context The self diffusivities of the four He isotopes are calculated using the Einstein relation (Einstein, 1956):
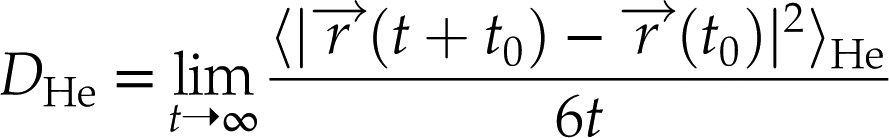Eq. 2
where 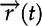represents the particle trajectories and 〈…〉He denotes average mean square displacement (MSD) over time from different time origins t0.
View in article
Guillot, B., Sator, N. (2012) Noble gases in high-pressure silicate liquids: A computer simulation study. Geochimica et Cosmochimica Acta 80, 51–69.
Show in context The predicted diffusivity for 4He in model basalt melt at 1623 K is 4.81 × 10−9 m2/s, which agrees well with the experimental value of 5 × 10−9 m2/s in a tholeiitic melt (Lux, 1987) and the computational result from classical MD in a MORB melt (Guillot and Sator, 2012), although it is unclear why an experiment reported a much lower value of 0.28 × 10−9 m2/s in model basalt melt at 1673 K (Amalberti et al., 2018).
View in article
Holycross, M.E., Watson, E.B., Richter, F.M., Villeneuve, J. (2018) Diffusive fractionation of Li isotopes in wet, highly silicic melts. Geochemical Perspectives Letters 6, 39–42.
Show in context All data shown here are for the relatively narrow temperature range 1623–1800 K, except one data point from Holycross et al. (2018).
View in article
Experimental data is from Richter et al. (2003, 2009), Watkins et al. (2009, 2011), and Holycross et al. (2018).
View in article
Karki, B.B., Ghosh, D.B., Bajgain, S.K. (2018) Chapter 16 - Simulation of Silicate Melts Under Pressure. In: Kono, Y., Sanloup, C. (Eds.) Magmas Under Pressure. First Edition, Elsevier, Amsterdam, 419–453.
Show in context The smaller activation energies predicted by FPMD simulations compared to experimental results have been extensively reported (Karki et al., 2018).
View in article
Kurz, M.D., Jenkins, W.J. (1981) The distribution of Helium in oceanic basalt glasses. Earth and Planetary Science Letters 53, 41–54.
Show in context No experiments have reported activation energy for He diffusion in silicate melts. The experimental activation energies for He diffusion in albite and basalt glasses at much lower temperatures (398–673 K) are 31.7 (Shelby and Eagan, 1976) and 83 ± 4 kJ/mol (Kurz and Jenkins, 1981), respectively.
View in article
Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2020) First-principles computation of diffusional Mg isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 290, 27–40.
Show in context First principles molecular dynamics (FPMD) simulations are reliable to calibrate β in liquids (Luo et al., 2020), but the high computational cost makes them unsuitable to deal with trace elements (e.g., noble gases and Li).
View in article
The decreasing trend of β with temperature in silicate melts around zero pressure has been reported in the simulations of diffusional Mg and Li isotope fractionation (Luo et al., 2020, 2021).
View in article
Note that Luo et al. (2020, 2021) stressed that this positive correlation only works at a constant or narrowly defined temperature range as β in silicate melts is found to decrease with decreasing temperature while Di/DSi increases. The correlation of β for He with DHe/DSi at 1700 K broadly follows the previous positive trend (Fig. 3).
View in article
As suggested in previous studies (e.g., Bourg and Sposito, 2007; Luo et al., 2020), only the first part of MSD curves in the diffusive regime (9–10 picoseconds (ps), 20–40 ps, and 50–100 ps at 3000, 2200, and 1700 K, respectively) is used to approximate the infinite time limit in Equation 2.
View in article
Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2021) Deep neural network potentials for diffusional lithium isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 303, 38–50.
Show in context The decreasing trend of β with temperature in silicate melts around zero pressure has been reported in the simulations of diffusional Mg and Li isotope fractionation (Luo et al., 2020, 2021).
View in article
Note that Luo et al. (2020, 2021) stressed that this positive correlation only works at a constant or narrowly defined temperature range as β in silicate melts is found to decrease with decreasing temperature while Di/DSi increases. The correlation of β for He with DHe/DSi at 1700 K broadly follows the previous positive trend (Fig. 3).
View in article
Computational results of Li at 1800 K are from Luo et al. (2021).
View in article
A recently developed technique called deep potential molecular dynamics (DPMD) simulations (Wang et al., 2018; Zhang et al., 2018), which is based on potentials trained by deep neural networks using ab initio data and is orders of magnitude faster than FPMD with comparable ab initio accuracy, has been successfully applied to predict β for Li in silicate melts (Luo et al., 2021).
View in article
Lux, G. (1987) The behavior of noble gases in silicate liquids-solution, diffusion, bubbles and surafce effects, with applications to natural samples. Geochimica et Cosmochimica Acta 51, 1549–1560.
Show in context The experimental data (Lux87) for the diffusivity of He in a tholeiitic melt is from Lux (1987).
View in article
The predicted diffusivity for 4He in model basalt melt at 1623 K is 4.81 × 10−9 m2/s, which agrees well with the experimental value of 5 × 10−9 m2/s in a tholeiitic melt (Lux, 1987) and the computational result from classical MD in a MORB melt (Guillot and Sator, 2012), although it is unclear why an experiment reported a much lower value of 0.28 × 10−9 m2/s in model basalt melt at 1673 K (Amalberti et al., 2018).
View in article
Moreira, M. (2013) Noble Gas Constraints on the Origin and Evolution of Earth’s Volatiles. Geochemical Perspectives 2, 229–230.
Show in context Only physical processes such as diffusion, adsorption, or ion implantation may cause significant elemental and isotopic fractionations (Moreira, 2013).
View in article
The inert behaviour combined with the existence of both radiogenic and non-radiogenic isotopes for each noble gas provides powerful tools for constraining mantle degassing history and identifying long lived heterogeneities within the mantle (Behrens, 2010; Moreira, 2013; Moreira and Kurz, 2013).
View in article
Moreira, M.A., Kurz, M.D. (2013) Noble Gases as Tracers of Mantle Processes and Magmatic Degassing. In: Burnard P. (Ed.) The Noble Gases as Geochemical Tracers. Advances in Isotope Geochemistry. First Edition, Springer-Verlag, Berlin, Heidelberg, 371–391.
Show in context However, measured noble gas isotope ratios in mid-ocean ridge basalts (MORB) and oceanic island basalts (OIB) are often difficult to interpret due to possible fractionations that happen in magma degassing (Moreira and Kurz, 2013).
View in article
The inert behaviour combined with the existence of both radiogenic and non-radiogenic isotopes for each noble gas provides powerful tools for constraining mantle degassing history and identifying long lived heterogeneities within the mantle (Behrens, 2010; Moreira, 2013; Moreira and Kurz, 2013).
View in article
Richter, F.M., Liang, Y., Davis, A.M. (1999) Isotope fractionation by diffusion in molten oxides. Geochimica et Cosmochimica Acta 63, 2853–2861.
Show in context Diffusional separation of isotopes can be expressed as (Richter et al., 1999):
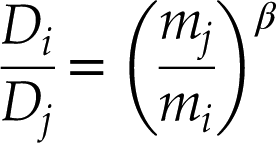Eq. 1
where Di and Dj are diffusion coefficients of two isotopes whose masses are mi and mj and β is a dimensionless empirical parameter.
View in article
The linear correlation of logD with logM in Figure 2b is consistent with the empirical Equation 1 proposed by Richter et al. (1999).
View in article
In comparison, magma degassing in an open system may be diffusion controlled (Watson, 2017) and diffusion can fractionate isotopes considerably even at magmatic temperatures (e.g., Richter et al., 1999; Watkins et al., 2017).
View in article
Richter, F.M., Davis, A.M., DePaolo, D.J., Watson, E.B. (2003) Isotope fractionation by chemical diffusion between molten basalt and rhyolite. Geochimica et Cosmochimica Acta 67, 3905–3923.
Show in context Experimental data is from Richter et al. (2003, 2009), Watkins et al. (2009, 2011), and Holycross et al. (2018).
View in article
Richter, F.M., Watson, E.B., Mendybaev, R., Dauphas, N., Georg, B., Watkins, J., Valley, J. (2009) Isotopic fractionation of the major elements of molten basalt by chemical and thermal diffusion. Geochimica et Cosmochimica Acta 73, 4250–4263.
Show in context Experimental data is from Richter et al. (2003, 2009), Watkins et al. (2009, 2011), and Holycross et al. (2018).
View in article
Shelby, J.E. (1971) Diffusion of Helium isotopes in vitreous silica. Physical Review B 4, 2681–2686.
Show in context The results from previous diffusion experiments using silicate glasses (Shelby, 1971; Trull and Kurz, 1999) may not be extrapolated to the cases in silicate melts, although silicate glasses are widely regarded as proper structural analogues of silicate melts.
View in article
Shelby, J.E., Eagan, R.J. (1976) Helium migration in sodium aluminosilicate glasses. Journal of the American Ceramic Society 59, 420–425.
Show in context No experiments have reported activation energy for He diffusion in silicate melts. The experimental activation energies for He diffusion in albite and basalt glasses at much lower temperatures (398–673 K) are 31.7 (Shelby and Eagan, 1976) and 83 ± 4 kJ/mol (Kurz and Jenkins, 1981), respectively.
View in article
Trull, T.W., Kurz, M.D. (1999) Isotopic fractionation accompanying helium diffusion in basaltic glass. Journal of Molecular Structure 485, 555–567.
Show in context The results from previous diffusion experiments using silicate glasses (Shelby, 1971; Trull and Kurz, 1999) may not be extrapolated to the cases in silicate melts, although silicate glasses are widely regarded as proper structural analogues of silicate melts.
View in article
Wang, H., Zhang, L.F., Han, J.Q., E, W. (2018) DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Computer Physics Communications 228, 178–184.
Show in context A recently developed technique called deep potential molecular dynamics (DPMD) simulations (Wang et al., 2018; Zhang et al., 2018), which is based on potentials trained by deep neural networks using ab initio data and is orders of magnitude faster than FPMD with comparable ab initio accuracy, has been successfully applied to predict β for Li in silicate melts (Luo et al., 2021).
View in article
Watkins, J.M., DePaolo, D.J., Huber, C., Ryerson, F.J. (2009) Liquid composition-dependence of calcium isotope fractionation during diffusion in molten silicates. Geochimica et Cosmochimica Acta 73, 7341–7359.
Show in context Experimental data is from Richter et al. (2003, 2009), Watkins et al. (2009, 2011), and Holycross et al. (2018).
View in article
Watkins, J.M., DePaolo, D.J., Ryerson, F.J., Peterson, B.T. (2011) Influence of liquid structure on diffusive isotope separation in molten silicates and aqueous solutions. Geochimica et Cosmochimica Acta 75, 3103–3118.
Show in context It has been proposed that β positively correlates with solvent normalised diffusivity (Di/DSi), implying that cations that are easier to decouple from the silicate matrix exhibit a larger diffusional isotope fractionation (Watkins et al., 2011, 2017).
View in article
Experimental data is from Richter et al. (2003, 2009), Watkins et al. (2009, 2011), and Holycross et al. (2018).
View in article
Watkins, J.M., DePaolo, D.J., Watson, E.B. (2017) Kinetic Fractionation of Non-Traditional Stable Isotopes by Diffusion and Crystal Growth Reactions. Non-Traditional Stable Isotopes 82, 85–125.
Show in context The reason is that the dynamics of silicate networks in high temperature melts help open and close paths for noble gas diffusion, which may play a key role in determining diffusional isotope fractionation (Behrens, 2010; Watkins et al., 2017).
View in article
It has been proposed that β positively correlates with solvent normalised diffusivity (Di/DSi), implying that cations that are easier to decouple from the silicate matrix exhibit a larger diffusional isotope fractionation (Watkins et al., 2011, 2017).
View in article
In comparison, magma degassing in an open system may be diffusion controlled (Watson, 2017) and diffusion can fractionate isotopes considerably even at magmatic temperatures (e.g., Richter et al., 1999; Watkins et al., 2017).
View in article
Watson, E.B. (2017) Diffusive fractionation of volatiles and their isotopes during bubble growth in magmas. Contributions to Mineralogy and Petrology 172, 61.
Show in context In comparison, magma degassing in an open system may be diffusion controlled (Watson, 2017) and diffusion can fractionate isotopes considerably even at magmatic temperatures (e.g., Richter et al., 1999; Watkins et al., 2017).
View in article
Yeh, I.-C., Hummer, G. (2004) System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. The Journal of Physical Chemistry B 108, 15873–15879.
Show in context The finite size effect on the diffusivities of He isotopes is insignificant within error after considering the correction relation proposed by Yeh and Hummer (Yeh and Hummer, 2004).
View in article
Zhang, L.F., Han, J.Q., Wang, H., Saidi, W., Car, R., E, W. (2018) End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. Advances of the Neural Information Processing Systems 31, 4441–4451.
Show in context A recently developed technique called deep potential molecular dynamics (DPMD) simulations (Wang et al., 2018; Zhang et al., 2018), which is based on potentials trained by deep neural networks using ab initio data and is orders of magnitude faster than FPMD with comparable ab initio accuracy, has been successfully applied to predict β for Li in silicate melts (Luo et al., 2021).
View in article
Zhang, Y.Z., Wang, H.D., Chen, W.J., Zeng, J.Z., Zhang, L.F., Wang, H., E, W. (2020) DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Computer Physics Communications 253, 107206.
Show in context The major technical improvement in this study is that the deep potential generator (DP-GEN) (Zhang et al., 2020) is used to achieve a concurrent learning procedure and to obtain a representative training data set in a rigorous way (Supplementary Information).
View in article
top
Supplementary Information
The Supplementary Information includes:
Download the Supplementary Information (PDF).
Figures
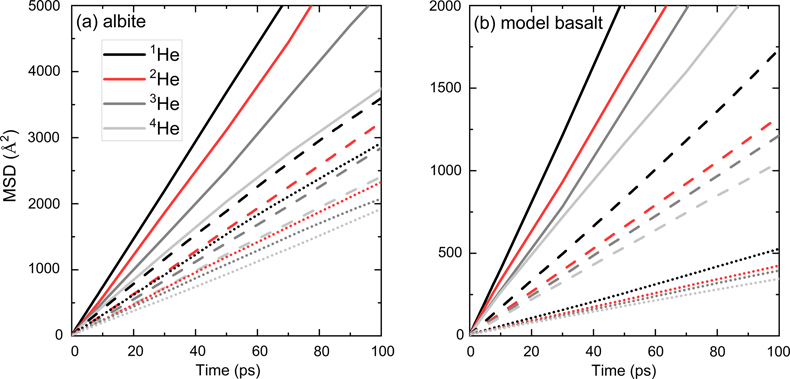
Figure 1 Mean square displacement (MSD) of He isotopes (1He, 2He, 3He, 4He) as a function of time in (a) albite and (b) model basalt melts at 3000 (solid lines), 2200 (dashed lines), and 1700 K (dotted lines) around zero pressure.
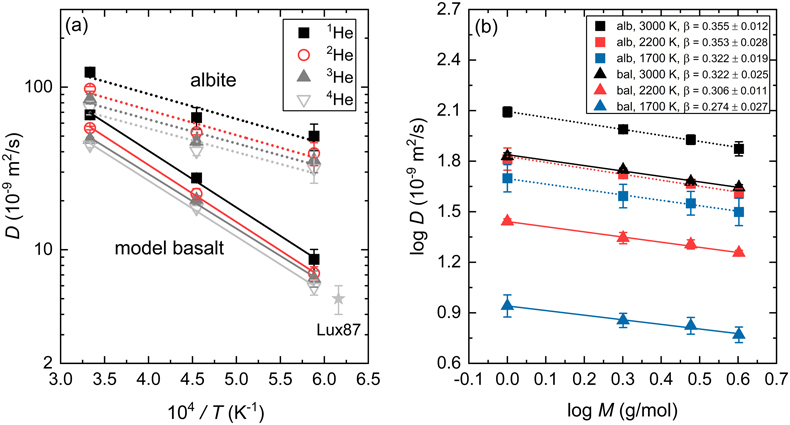
Figure 2 (a) Diffusion coefficients of He isotopes (1He, 2He, 3He, 4He) as a function of temperature in albite and model basalt melts around zero pressure. The experimental data (Lux87) for the diffusivity of He in a tholeiitic melt is from Lux (1987)
Lux, G. (1987) The behavior of noble gases in silicate liquids-solution, diffusion, bubbles and surafce effects, with applications to natural samples. Geochimica et Cosmochimica Acta 51, 1549–1560.
. (b) Log-log plot of the diffusivities of He isotopes in albite (alb) and model basalt (bal) melts as a function of isotopic mass at different temperatures around zero pressure.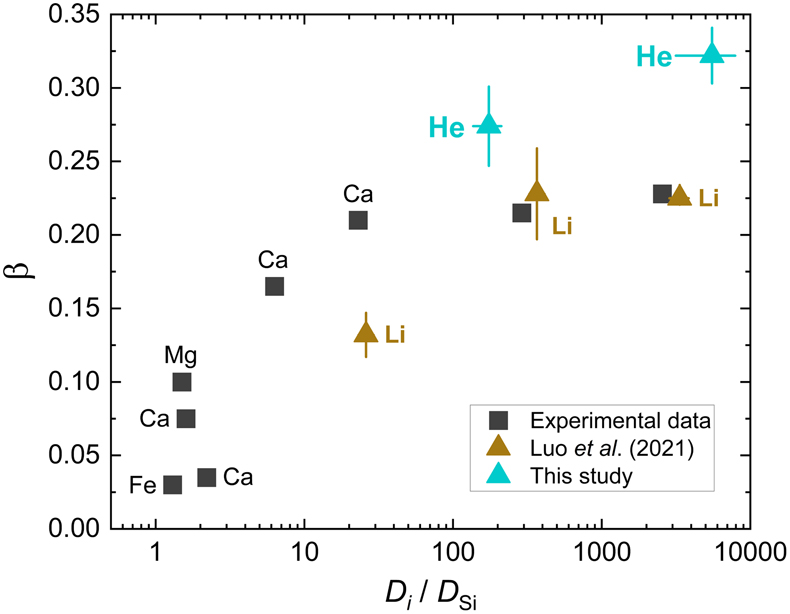
Figure 3 Relationship of β with solvent normalised diffusivity (Di/DSi). Experimental data is from Richter et al. (2003
Richter, F.M., Davis, A.M., DePaolo, D.J., Watson, E.B. (2003) Isotope fractionation by chemical diffusion between molten basalt and rhyolite. Geochimica et Cosmochimica Acta 67, 3905–3923.
, 2009Richter, F.M., Watson, E.B., Mendybaev, R., Dauphas, N., Georg, B., Watkins, J., Valley, J. (2009) Isotopic fractionation of the major elements of molten basalt by chemical and thermal diffusion. Geochimica et Cosmochimica Acta 73, 4250–4263.
), Watkins et al. (2009Watkins, J.M., DePaolo, D.J., Huber, C., Ryerson, F.J. (2009) Liquid composition-dependence of calcium isotope fractionation during diffusion in molten silicates. Geochimica et Cosmochimica Acta 73, 7341–7359.
, 2011Watkins, J.M., DePaolo, D.J., Ryerson, F.J., Peterson, B.T. (2011) Influence of liquid structure on diffusive isotope separation in molten silicates and aqueous solutions. Geochimica et Cosmochimica Acta 75, 3103–3118.
), and Holycross et al. (2018)Holycross, M.E., Watson, E.B., Richter, F.M., Villeneuve, J. (2018) Diffusive fractionation of Li isotopes in wet, highly silicic melts. Geochemical Perspectives Letters 6, 39–42.
. Computational results of Li at 1800 K are from Luo et al. (2021)Luo, H., Karki, B.B., Ghosh, D.B., Bao, H. (2021) Deep neural network potentials for diffusional lithium isotope fractionation in silicate melts. Geochimica et Cosmochimica Acta 303, 38–50.
. All data shown here are for the relatively narrow temperature range 1623–1800 K, except one data point from Holycross et al. (2018)Holycross, M.E., Watson, E.B., Richter, F.M., Villeneuve, J. (2018) Diffusive fractionation of Li isotopes in wet, highly silicic melts. Geochemical Perspectives Letters 6, 39–42.
.
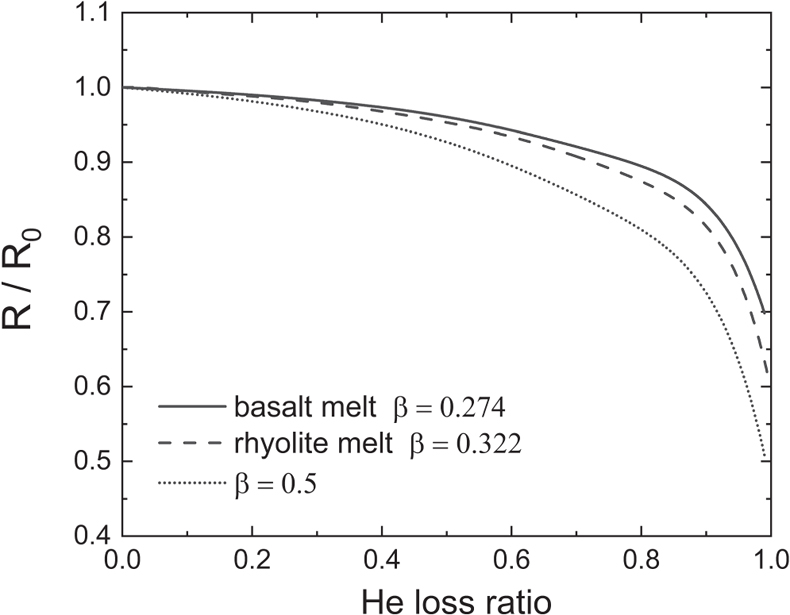
Figure 4 (3He/4He)/(3He/4He)0 as a function of He loss ratio for different β values.